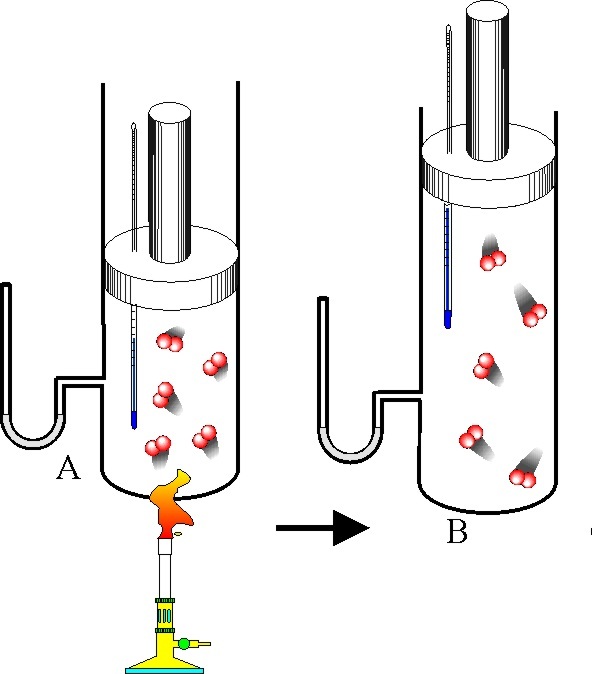
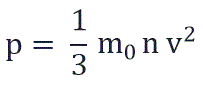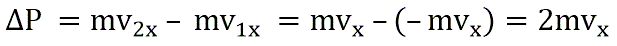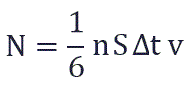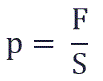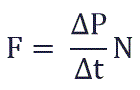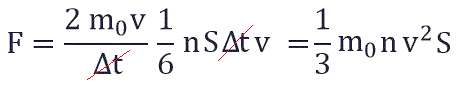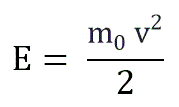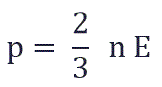Вычислите концентрацию молекул газа n выразив ее из основного уравнения мкт (7 видео)

Основное уравнение молекулярно-кинетической теории (МКТ) с выводом

В статье рассмотрена модель идеального газа, приведено основное уравнение молекулярно-кинетической теории и его вывод.

Чтобы объяснить свойства материи в газообразном состоянии, в физике применяется модель идеального газа. Идеальный газ — разреженный, состоящий из одного типа атомов газ, частицы которого не взаимодействуют между собой. Помимо основных положений МКТ эта модель предполагает, что:

молекулы имеют пренебрежимо малый объем в сравнении с объемом емкости
при сближении частиц друг с другом и с границами емкости имеют место силы отталкивания

Содержание

Основное уравнение молекулярно-кинетической теории
Вывод основного уравнения МКТ
Вычислите концентрацию молекул газа n выразив ее из основного уравнения мкт
Идеальный газ. Формула концентрации молекул газа. Пример задачи
Идеальный газ
Универсальное уравнение
Понятие о концентрации молекул: виды концентраций
Формула концентрации молекул газа
Пример задачи
🔥 Видео

Видео:Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Основное уравнение молекулярно-кинетической теории

Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа — это совокупность всех ударов молекул о стенки сосуда. Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:

p – давление молекул газа на границы емкости,

m₀ – масса одной молекулы,

n — концентрация молекул, число частиц N в единице объема V;

v 2 — средне квадратичная скорость молекул.

Видео:Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать

Вывод основного уравнения МКТ

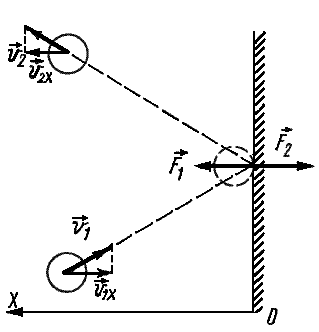
Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция v_x скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:

Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv_1x = –mv_x на mv_2x = mv_x.

Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:

Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6. Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:

S – площадь этой стенки

n — концентрация частиц

Давление p равно отношению силы F к площади S, на которую действует эта сила:

Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:

Исходя из вышенаписанного получаем:

Если заменить среднее значение кинетической энергии поступательного движения молекул — E:

и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:

Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.

Понравилась статья, расскажите о ней друзьям:

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Вычислите концентрацию молекул газа n выразив ее из основного уравнения мкт

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Найти концентрацию газа при нормальных условиях. Постоянная Больцмана k = 1,38·10 -23 Дж/К.

Дано:

Решение:

Связь давления и концентрации

Концентрация газа при нормальных условиях

Ответ:

Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Идеальный газ. Формула концентрации молекул газа. Пример задачи

В физике текучих субстанций большое внимание уделяется изучению газов, которое осуществляют при помощи использования модели идеального газа. В этой области было открыто много законов. В приведенной ниже статье изучим формулу концентрации молекул газа (идеального) и покажем, как ее следует применять при решении практической проблемы.

Видео:Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

Идеальный газ

Что же это такое? Прежде чем записать формулу концентрации молекул газа, расскажем, что собой представляет модель идеального газа. В соответствии с кинетической теорией текучих субстанций, в таких веществах молекулы и атомы движутся хаотически по прямым траекториям. Расстояния между ними намного больше, чем их собственные линейные размеры, поэтому последними пренебрегают при выполнении вычислений. Кроме того, считают, что взаимодействий между молекулами не существует, поскольку их кинетическая энергия слишком велика по сравнению со слабыми потенциальными взаимодействиями.

Любые реальные газы, которые находятся при низких давлениях и достаточно высоких абсолютных температурах, по своему поведению приближаются к описанной модели. Тем не менее существуют текучие субстанции, у которых помимо ван-дер-ваальсовых взаимодействий между частицами действуют взаимодействия более сильного характера. Примером является водяной пар, у которого молекулы друг с другом связаны водородными (полярными) связями. Для описания поведения таких субстанций нельзя использовать модель идеального газа.

Видео:Секретный вывод основного уравнения МКТСкачать

Универсальное уравнение

Модель идеального газа удобна при выполнении практических расчетов тем, что уравнение состояния вещества, полученное на ее основе, связывает три термодинамических параметра: температуру T, объем системы V и абсолютное давление P. Это уравнение записано ниже:

Где R — постоянная, равная 8,314 Дж/(моль*К), n — количество вещества.

Современная молекулярно-кинетическая теория газов позволяет путем несложных рассуждений и математических выкладок получить теоретически это уравнение. Впервые же оно было записано в результате анализа многочисленных экспериментов, которые в течение двух веков выполняли европейские ученые, начиная от Роберта Бойля (вторая половина XVII века) и заканчивая Амедео Авогадро (начало XIX века).

Считается, что уравнение состояния идеального газа первым получил Эмиль Клапейрон, а к современной форме его привел русский химик Дмитрий Менделеев, поэтому его часто называют законом Клапейрона-Менделеева.

Видео:Урок 146. Основное уравнение МКТ идеального газа - 2Скачать

Понятие о концентрации молекул: виды концентраций

Когда изучают текучие субстанции, то знать концентрации компонентов, которые их образуют, является важным при решении многих практических задач. Например, от этого показателя и размеров молекул зависит общая площадь поверхности активного вещества, а значит, его реакционная способность. Другой пример, концентрация некоторых веществ в воздухе определяет допустимые их пределы для нормального протекания жизненно необходимых процессов в организме человека.

В случае газов, как правило, пользуются тремя следующими концентрациями:

Атомная. Она определяется, как процентное содержание количества атомов или молекул компонента по отношению к объему всей системы.
Массовая. Показывает отношение массы компонента к объему газа.
Молярная. Она равна отношению количества вещества изучаемого компонента к объему системы.

Заметим, что все виды концентраций вычисляются по отношению к объему системы. Справедливость этих величин действительна, поскольку каждый компонент системы полностью заполняет ее объем.

Среди всех типов концентраций наиболее удобной на практике является молярная. Ниже в статье приведем формулу именно для нее.

Видео:Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать

Формула концентрации молекул газа

В соответствии с приведенным в предыдущем пункте определением, молярная концентрация i-го компонента системы c_n(i) вычисляется так:

Предположим, что мы имеем однокомпонентный (чистый) газ. Это может быть кислород, азот, гелий и так далее. В этом случае можно применить формулу Клапейрона-Менделеева и выразить из нее молярную концентрацию молекул. Имеем:

c_n = n / V = P / (R * T).

Из записанной формулы концентрации молекул газа легко получить атомную (молекулярную) концентрацию. Покажем, как это делается:

Здесь N_A и k_B — число Авогадро и постоянная Больцмана. Соответственно, N — число молекул в системе. Поскольку величина k_B имеет маленькое значение (1,38 * 10 -23 ), то c_N принимает огромные значения, что неудобно для ее практического использования.

Видео:Физика 10 Идеальный газ Основное уравнение МКТ идеального газа Решение задачСкачать

Пример задачи

В результате изобарного нагрева закрытой системы с идеальным газом его температура увеличилась на 100 К и стала равной 400 К. Как изменится концентрация молекул газа, если давление в системе составляет 1,5 атмосферы.

Поскольку давление в процессе нагрева не изменилось, а температура была равна 300 К согласно условию задачи, то молярная концентрацию молекул до нагрева системы составляла:

c_n1 = 1,5 * 101 325 / (8,314 * 300) = 60,9 моль/м 3 .

Число молекул в системе не изменилось при нагреве, так как система является закрытой. После нагрева газа его концентрация составила:

c_n2 = 1,5 * 101 325 / (8,314 * 400) = 45,7 моль/м 3 .

Изменение концентрации составило:

Отрицательный знак говорит, что концентрация уменьшилась, что является очевидным, поскольку увеличился объем системы после нагрева, а число частиц в ней осталось прежним.