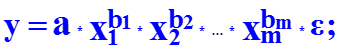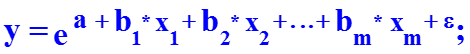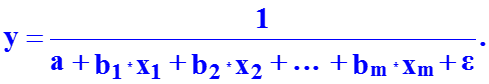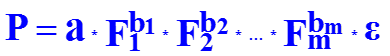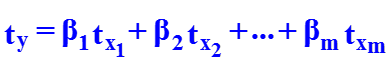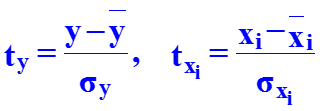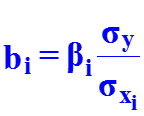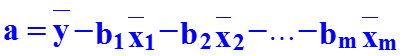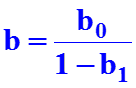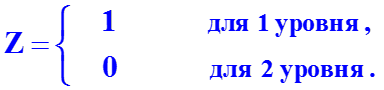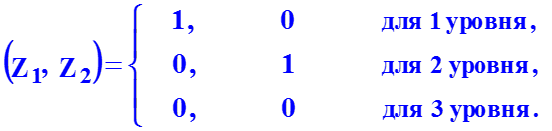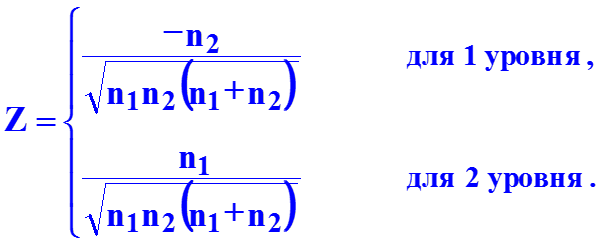Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать
Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
| Нелинейные по оцениваемым параметрам |
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
Видео:Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать
Множественная регрессия и корреляция.Спецификация модели множественной регрессии
Страницы работы
Фрагмент текста работы
Тема 4. Множественная регрессия и корреляция
4.1. Спецификация модели множественной регрессии 4.2. Оценка параметров уравнения множествен-ной регрессии 4.3. Множественная корреляция 4.4. Оценка надежности результатов множествен-ной регрессии и корреляции 4.5. Предпосылки метода наименьших квадратов и обобщенный МНК
4.1. Спецификация модели множественной регрессии
Спецификация модели – обоснованный с позиций экономической теории выбор вида и структуры модели, отбор факторов и математическое описание характера их влияния на результирующий признак
Если при построении эконометрической модели не удается выявить единственный фактор, оказывающий доминирующее влияние на исследуемый результативный признак, то вместо парной регрессии применяют множественную регрессию. Множественная регрессия – это уравнение связи зависимой переменной с несколькими независимыми переменными: y = f ( x1, x2, … , xm, e ), где y — зависимая переменная (результативный признак); x1, x2, … , xm — независимые переменные (факторы); e — случайная величина (остаток). Спецификация модели множественной регрессии включает выбор вида функции регрессии и отбор факторов.
Функции множественной регрессии
Для построения модели множественной регрессии чаще используются следующие функции: · линейная y = a + b1 * x1 + b2 * x2 + … + bm * xm + e ; · степенная · экспонента · гипербола · полином y = a + b1* x1 + b2* x2 + b3* x12 + b4 * x22 + b5*x1*x2 + e Можно использовать и другие функции, приводимые к линейному виду. Однако, при этом число наблюдений должно не менее, чем в 6 – 8 раз превышать число факторов и модель должна быть экономически интерпретируемой.
Степенная модель множественной регрессии применяется в производственных функциях вида : где P – количество продукта, изготавливаемого с помощью m производственных факторов объемом F1, F2, …, Fm; bi – эластичность количества продукции по отношению к объему i-го производственного фактора. Коэффициенты bi показывают, на сколько процентов изменяется результат с изменением соответствующего фактора на 1 процент. Сумма bi характеризует общую эластичность выпуска продукции, т.е. процент увеличения выпуска продукции при возрастании объема каждого фактора на 1 процент.
Стандартизованное уравнение линейной регрессии
В ряде случаев применяют линейное уравнение регрессии в стандартизованном масштабе: где — стандартизованные переменные; bi – стандартизованные коэффициенты регрессии. Коэффициенты bi позволяют ранжировать факторы по силе их влияния на результативный признак. Связь коэффи-циентов множественной регрессии bi со стандартизованными коэффициентами bi описывается соотношением Параметр a определяется как
Примеры множественной линейной регрессии
Расходы семьи на продукты питания y в зависимости от дохода на одного члена семьи x1 и размера семьи x2: y = a + b1 * x1 + b2 * x2 + e Уровень потребления в текущем периоде Ct в зависимости от дохода того же периода Rt и от дохода предшествующего периода Rt-1 : Ct = a + b0 * Rt + b1 * Rt-1 + e , b0 — краткосрочная предельная склонность к потреблению, b = b0 + b1 — долгосрочная склонность к потреблению. Функция потребления может рассматриваться также в зависимости от предыдущего уровня потребления Ct-1: Ct = a + b0 * Rt + b1 * Ct-1 + e , долгосрочная склонность к потреблению здесь равна:
Фиктивные переменные для качественных факторов
Факторы должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, то каждому его уровню следует тем или иным способом придать количественную определенность. С этой целью применяются фиктивные переменные. Если качественный фактор имеет два различимых уровня, то вводится одна фиктивная переменная Z, значения которой устанавливаются равными:
Если качественный фактор имеет три уровня, то вводятся две фиктивные переменные Z1 и Z2, значения которых устанавливаются равными:
Фиктивная переменная для качественного фактора с 2 уровнями
Факторы должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, то каждому его уровню следует тем или иным способом придать количественную определенность. С этой целью применяются фиктивные переменные. Если качественный фактор имеет два различимых уровня с n1 и n2 наблю-дениями, то вводится одна фиктивная переменная
Можно использовать значение 0 для первого уровня и 1 для второго уровня (или, наоборот).
Фиктивные переменные для качественного фактора с 3 уровнями
Видео:Математика #1 | Корреляция и регрессияСкачать
Составить уравнение множественной линейной регрессии y = a + b1x1 + b2x2 + ε в матричной форме
Составить уравнение множественной линейной регрессии y = a + b1x1 + b2x2 + ε в матричной форме, используя МНК, и найти числовые характеристики переменных.
Найти оценки параметров а, b1, b2, б².
Найти коэффициент детерминации и оценить уравнение регрессивной связи.
Построить корреляционную матрицу и оценить статистическую зависимость между переменными.
По данным, полученным от фермерских хозяйств одного из регионов, изучается зависимость объёма выпуска продукции растениеводства Y (млн руб.) от двух факторов: численности работников Х1 (чел.) и количества осадков в период вегетации Х2 (мм).
№ п/п Y Х1 Х2
1 0.9 54 5
2 1.3 62 7
3 2.4 80 13
4 2.6 83 11
5 3.2 98 18
Тогда .
Рассчитаем
11111546280839857131118∙15451627180131831119818=537754377296534421544421688
11111546280839857131118∙0,91,32,42,63,2=10,4850,6131.
Матрицу определим по формуле , где – определитель матрицы ; – матрица, присоединенная к матрице
Получим
A-1=26,2174-0,63222,0047-0,63220,0160-0,05352,0047-0,05350,1879.
Теперь умножим эту матрицу на вектор
10,4850,6131
Получим B=26,2174-0,63222,0047-0,63220,0160-0,05352,0047-0,05350,1879∙10,4850,6131=-2,47590,0668-0,0444.
e=e1e2e3e4e5=-0,0084-0,05390,11050,0213-0,0696
2.Найдем оценки параметров а, b1, b2, б².
Исходя из матрицы В=-2,47590,0668-0,0444 значения параметров а=-2,4759,
b1=0,0668; b2=-0,0444.
Уравнение множественной регрессии имеет вид:
.
3.Найдем коэффициент детерминации и оценим уравнение регрессивной связи.
Для удобства вычислений составим вспомогательную таблицу.
№ х12
х2 2
у2
1 0.9 54 5 0.9084 1.3924 1.373 0.000 2916 25 0.81
2 1.3 62 7 1.3539 0.6084 0.527 0.003 3844 49 1.69
3 2.4 80 13 2.2895 0.1024 0.044 0.012 6400 169 5.76
4 2.6 83 11 2.5787 0.2704 0.249 0.000 6889 121 6.76
5 3.2 98 18 3.2696 1.2544 1.415 0.005 9604 324 10.24
SYMBOL 83f “symbol” * MERGEFORMAT 10.4 377 54 10.4 3.628 3.608 0.020 29653 688 25.26
Ср.знач. 2.08 75.4 10.8 5930.6 137.6 5.052
Рассчитаем коэффициент детерминации:
Коэффициент детерминации свидетельствует о том, что вариация исследуемой зависимой переменной на 99,4% объясняется изменчивостью включенных в модель объясняющих переменных , .
Рассчитаем скорректированный коэффициент детерминации:
Оба коэффициента детерминации свидетельствуют о сильной связи между факторными переменными и результативным показателем.
Проверим статистическую значимость на основе критерия Фишера по формуле:
Фактическое значение критерия F меньше табличного , определенного на уровне значимости при и степенях свободы, т.е. уравнение регрессии статистически незначимо, следовательно, исследуемая зависимая переменная Y плохо описывается включенными в регрессионную модель переменными.
4.Построим корреляционную матрицу и оценим статистическую зависимость между переменными.
Рассчитаем стандартизированные коэффициенты регрессии , коэффициенты эластичности , и -коэффициенты.
Коэффициент эластичности рассчитывается по формуле
;.
Это означает, что увеличение переменной на 1% (от своего среднего значения) приводит в среднем к росту величины на 2,422%, увеличение переменной на 1% (от своего среднего значения) приводит в среднем к уменьшению величины на 0,230%.
Стандартизированный коэффициент регрессии рассчитывается по формуле
,
где
,.
Стандартизированный коэффициент регрессии показывает, на сколько величин изменится в среднем зависимая переменная при увеличении только j-ой объясняющей переменной на .
Таким образом, увеличение только на одно увеличивает в среднем зависимую величину Y на 1,228; увеличение только на одно уменьшает в среднем зависимую величину Y на 0,239.
Рассчитаем -коэффициенты:
,
где – коэффициент парной корреляции.
Найдем матрицу коэффициентов парной корреляции.
это означает, что на 123,0% приращение величины Y можно объяснить влиянием изменения фактора ,
это означает, что на 23,0% приращение величины Y можно объяснить влиянием изменения фактора .
user969511 5.0
Два высших образования (менеджмент в информационных технологиях, автоматизация технологических процессов).+аспирант философского факультета и лингвистики. Стаж: больше 5 лет работы над рефератами,докладами,решениями тех,лингв и эконом задач
📽️ Видео
Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать
Эконометрика. Линейная парная регрессияСкачать
Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать
Парная регрессия: линейная зависимостьСкачать
Уравнение регрессииСкачать
Множественная регрессияСкачать
Практика Многофакторная регрессияСкачать
Эконометрика. Множественная регрессия и корреляция.Скачать
Эконометрика Линейная регрессия и корреляцияСкачать
Множественная регрессия в ExcelСкачать
Множественная регрессия в программе Statistica (Multiple regression)Скачать
Метод наименьших квадратов. Линейная аппроксимацияСкачать
Множественная степенная регрессияСкачать
Точечный прогноз. Интервальный прогноз. Построение уравнения регрессии с помощью анализа данныхСкачать
Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать
Полиномиальная регрессияСкачать
Тема 5. Множественная регрессия.Скачать
