Уравнения сводящиеся к простейшим заменой неизвестного 10 класс никольский конспект урока

ПРОБЛЕМА: Как решить любое задание 13, содержащее тригонометрическое уравнение, на предстоящем экзамене?

Решение тригонометрических уравнений, сводящихся к алгебраическим.

Основные методы решения уравнений: применение формул, разложение на множители, введение новой переменной…

Просмотр содержимого документа
«Урок в 10 классе тема урока: « Решение тригонометрических уравнений, сводящихся к алгебраическим.»»

Терещенко Ирина Валентиновна

Муниципальное автономное общеобразовательное учреждение «Школа №17 города Белогорск» Амурской области

Урок математики в 10 классе по теме:
«Решение тригонометрических уравнений, сводящихся к алгебраическим»

Тема урока:
Решение тригонометрических уравнений, сводящихся к алгебраическим.

Цель урока: сформировать представление об алгебраических уравнениях;
познакомить учащихся с методами решения тригонометрических уравнений.

повторить: определение и способы решения простейших тригонометрических уравнений; определение квадратного уравнения, формулы дискриминанта и корней квадратного уравнения

сформировать знания об отличительных признаках и способах решения тригонометрических уравнений, сводящихся к алгебраическим.

уметь: выделять среди тригонометрических уравнений тригонометрические уравнения, сводящиеся к алгебраическим и решать их.

развивать логическое мышление учащихся, память, внимание, речь; умения рассуждать и выделять главное; умение самостоятельно приобретать знания и применять их на практике, развивать навыки самоконтроля и взаимоконтроля.

воспитывать уважительное отношение к одноклассникам, самостоятельность, ответственность, эстетический вкус, аккуратность, интерес к математике.

Оборудование: мультимедийный проектор, экран, лист самооценки.

1. Организационный момент, формирование мотивации работы учащихся (2 мин.)

Здравствуйте, садитесь. Эпиграфом к уроку я взяла такие слова : “Сегодня – мы учимся вместе: я, ваш учитель и вы мои ученики. Но в будущем ученик должен превзойти учителя, иначе в науке не будет прогресса ”. (Сухомлинский Василий Александрович) Структура урока

Организационный момент — 1 мин

Проверка домашнего задания 1 мин

Актуализация знаний (работа в парах, фронтальная работа) – 10 мин

II. Основная часть урока

Постановка проблемной ситуации – 1 мин

Изучение нового материала и решение проблемного вопроса – 15 мин

III. Рефлексивно-оценочная часть урока

Закрепление (самостоятельная работа) – 8 мин

Информация о домашнем задании – 2 мин

У каждого есть критерии работы на уроке, задания на урок, оценочный лист. Подпишите его, каждый этап урока вам необходимо оценивать, в конце урока необходимо сдать, оценив свою работу на уроке.

2. Формулирование темы, цели урока.

Решение простейших тригонометрических уравнений. Существуют ли другие типы тригонометрических уравнений? (Да. Если есть «простейшие», то значит, есть более сложные. Исходя из выше сказанного, предлагает сформулировать тему сегодняшнего урока (Решение сложных/других/различных типов тригонометрических уравнений). Тригонометрические уравнения, сводящиеся к алгебраическим (записать дату, тему на доске).
«Величие человека – в его способности мыслить» Блез Паскаль

На столе у каждого из учащихся находятся шаблоны яблок . Написать на «яблоках» свои ожидания от урока. После этого все шаблоны яблок прикрепляются. Получается «Дерево ожиданий».

Как отличить от других?

Кто придумал алгоритм решения?

Сколько корней может быть?

В конце урока проверим сбылись ожидания.

«. Математика — это цепь понятий: выпадет одно звенышко — и не понятно будет дальнейшее» Н.К. Крупская

I. Проверка домашнего задания (Каждый ученик сам оценивает свою работу)

«5»- задание выполнено верно и самостоятельно «4»- задание выполнено верно и полностью, но часть задания выполнена с помощью одноклассников «3»-интересовался решением и все решил с помощью одноклассников.

sin (x+ 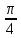)=1

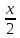
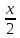
cos 2 — sin 2 = —

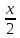
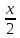
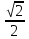
Сколько корней имеет уравнение 2sin cos = на отрезке [0; 2π]

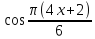
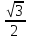
Найдите корень уравнения = . В ответе запишите наименьший положительный корень.

3. Актуализация знаний и подготовка учащихся к активному и сознательному усвоению нового материала (10 мин.).

I Вспомним главное…Фронтальная работа (устно)

При каких значениях а имеют смысл выражения: arcsin a; arcсos a.

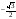
Вычислите: arcsin 0,5; arcсos ( ), arcsin( ); аrcsin 1 ; arcсos (-1); arcsin 0; arcсos1;

arcsin (-1) ; arcсos (-0,5).

Как решить линейное, квадратное, кубическое, биквадратное уравнения?

Дайте определение тригонометрического уравнения.

Сколько корней может иметь тригонометрическое уравнение?

Какое уравнение называется простейшим?

Назовите решение простейших уравнений?

Какие способы решения тригонометрических уравнений вы знаете?

Основное тригонометрическое тождество.

II.Самостоятельная работа (Кодирование «Уравнение — корни» (Работа в тетрадях) 3 минуты

3. sinх = —

4. cosх =

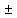
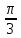
2. х = + 2πn, nϵ Z

4. х = (-1) n +1 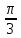+ πn, nϵ Z

5. х = ± 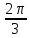+ 2πn, nϵ Z

4. cosх = —

6. sinх =

1. x = ± arccos a + 2πn, nϵ Z

2. х = 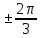+2 πn, nϵ Z

3. х = — 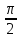+ 2πn, nϵ Z

4. х = 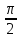+ 2πn, nϵ Z

5. х = (-1) n 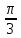+ πn, nϵ Z

6. х = 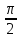+ πn, nϵ Z

Оценивание: 6 верно решенных примера — оценка «5» 4- 5 – «4» 3 – «3» менее 3 – «2»

III. В каждом из приведенных примеров сделаны ошибки. Назовите верный ответ и подумайте о причине ошибки. (Решение уравнений в тетрадях или устно) работа в группах

cos x= 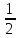, х = ± + 2πк, к Z

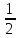
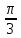
Верно: cos x= , х = ± + 2πк, к Z

Ошибка в вычислении значений тригонометрической функции

Ошибка в формуле нахождения решения уравнения sin x =a

Ошибка в выполнении деления

4. Этап усвоения новых знаний и способов действий (15 мин.).

Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важней. Политика существует только для данного момента, а уравнения будут существовать вечно. Альберт Эйнштейн

Уметь: различать вид тригонометрического уравнения

Знать: способ решения тригонометрического уравнения.

ПРОБЛЕМА: Как решить любое задание 15, содержащее тригонометрическое уравнение, на предстоящем экзамене?

Решение тригонометрических уравнений, сводящихся к алгебраическим.

Основные методы решения уравнений: применение формул, разложение на множители, введение новой переменной…

Алгоритм решения методом замены уравнений, сводящимся к алгебраическим

1. Привести уравнение к алгебраическому виду относительно одной из тригонометрических функций

2. Обозначить полученную функцию переменной, обозначив ее ограничения

3. Записать и решить полученное алгебраическое уравнение

4. Вернуться к замене

5. Решить простейшее тригонометрическое уравнение

5. РЕШИТЬ УРАВНЕНИЯ:

1. 2sin² x — 3 sin x — 2 = 0

3. 6sin² x + 5 cos2x — 7 = 0

4. Единый государственный экзамен, 2015 Математика, 11 класс 26.03.15 Досрочный Образец варианта

2cos 3 х — cos ² x + 2 cos x -1 = 0

6. Этап первичной проверки понимания изученного (5 мин.)

Работа дифференцированная, каждый уровень сложности заданий представлен в двух вариантах.
I уровень – «3», II уровень – «4», III уровень – «5» в случае полного правильного решения. Работа будет проверена учителем к следующему уроку, отметки будут выставлены за урок.

7. Этап рефлексии и оценивания. Подведение итогов урока (2 мин.).

— Что нового узнали на уроке?

— Испытывали ли вы затруднения при выполнении самостоятельной работы?

— Испытывали ли вы затруднения при выборе самостоятельной работы?

— Какие пробелы выявились на уроке?

— Какие проблемы у вас возникли по окончании урока?

ОБРАТИМСЯ К ДЕРЕВУ ОЖИДАНИЙ, СТАЛ ЛИ ОН ДЛЯ НАС ДЕРЕВОМ ЖЕЛАННИЙ. Ведь они чаще всего сбываются.

8. Этап информирования учащихся о домашнем задании § 4 стр 322

1группа стр.327 №51(2,4)

2группа стр 327 №56(2), 57(2)

Дополнительно: Досрочный ЕГЭ 2015. Решите уравнение

Учитель: Дорогое ребята! Спасибо вам за работу на уроке. Я благодарю всех, кто принял активное участие в работе. Благодарю вас за помощь в проведении урока. Надеюсь на дальнейшее сотрудничество. Урок окончен. До свидания!
Спасибо вам, ребята, за работу,
Не подвели меня и в этот раз,
С великим удовольствием, конечно,
Поставлю вам оценки я сейчас!

Видео:Алгебра 10 класс. Уравнения, сводящиеся к простейшим заменой неизвестногоСкачать

конспект урока «Решение показательных уравнений, сводящихся к простейшим заменой»
план-конспект урока по алгебре (10 класс) на тему

открытый урок на конкурс учитель года

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Скачать:

Видео:Занятие 11. Уравнения, сводящиеся к простейшимСкачать

Предварительный просмотр:

Тема: Показательные уравнения, сводящиеся к простейшим заменой

Цель: Закрепить понятие «показательное уравнение»; формирование умений и навыков решения показательных уравнений; научить решать однородные показательные уравнения.

Развивать вычислительные навыки и умения, логическое мышление учащихся.

Воспитывать навыки сотрудничества и ответственное отношение к обучению.

Оборудование: доска, карточки.

Форма урока : классно-урочная

Вид урока : практическое занятие с элементами лекции.

Тип урока : комбинированный.

1. Организационный момент
2. Проверка домашнего задания. Актуализация опорных знаний
3. Изучение нового материала
4. Закрепление изученного материала
5. Самостоятельная работа.
6. Подведение итогов
7. Задание на дом

— Здравствуйте, я учитель математики Кулик И. А. сегодня проведу урок по теме «Показательные уравнения, сводящиеся к простейшим заменой»

1. Проверка домашнего задания:

Вставить пропущенные символы…

Актуализация опорных знаний

Цель: подготовить учащихся к восприятию нового материала

Устный счет: 2¹, 2 ², 3 °, 3⁻², 10 ⁻²,7 ⁻², (1/4) °, (3/2)°, (3/2) ⁻¹, (3/7)²,

1. Какие уравнения называются показательными? Показательными уравнениями называют уравнения вида , где — положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
2. Какой основной метод решения показательных уравнений? Сведение к одинаковому основанию. Теорема: Показательное уравнение (где , ) равносильно уравнению .
3. Какие способы решения показательных уравнений вы знаете еще?

Вынесение общего множителя за скобки, замена.

1. Давайте назовем методы решения предложенных уравнений: учебник с. 378-379

№ 132 – сведение к одинаковому показателю

№ 134 – вынесение общего множителя за скобки

№ 139 – заменой (Этим методом вы решали показательные уравнения на прошлом занятии).

1. Изучение нового материала

Цель: сформулировать понятие «однородное показательное уравнение», показать методы решения.

Метод: объяснение учителя

. Перепишем данное уравнение с учетом, что: , , . Получаем уравнение — . Перенесём правую часть уравнения в левую: . Разделим обе части уравнения на , получим

Данное уравнение решается методом введения новой переменной: , тогда уравнение примет вид . Решив квадратное уравнение относительно , находим: , т.е. и . Но , значит, нам остается решить два уравнения: и (что то же ). Первое уравнение не имеет решения, так как , второе показательное уравнение решаем методом уравнивания коэффициентов, и получаем ответ: .

— Рассмотренное нами только что уравнение носит название «однородное уравнение» и решается делением на одну из показательных функций.

1. Закрепление изученного материала № 146(а)

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Конспект урока по алгебре и началам математического анализа на тему » Уравнения, сводящиеся к простейшим заменой неизвестного » (10 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

• Свидетельства для портфолио
• Вечный доступ за 120 рублей
• 311 видеолекции для каждого

УРОК № 3 Тема 6. Показательные и логарифмические уравнения и неравенства (11ч)

Тема урока. Уравнения, сводящиеся к простейшим заменой неизвестного.

Цель урока : Сформировать навыки решения показательных уравнений, способом приведения к одинаковому основанию и уравнений, сводящиеся к простейшим, заменой неизвестного .

Тип урока: комбинированный.

Проверка домашнего задания .

Актуализация опорных знаний.

1. Какие уравнения называются показательными?

2. Объясните, в каких случаях показательное уравнение a x =b (где a>0 и a≠1) имеет корни. В каких случаях это уравнение не имеет корней?

Объяснение нового материала и его поэтапное закрепление.

1.1. Объяснение нового материала.

Решите уравнение: ,

,

1.2. Поэтапное закрепление.

№ 6.16(в,г). Решите уравнения. № 6.17(д). Решите уравнения.

в) , г) , д) ,

, , ,

-3х + 1 = 4, х – 6 = -2, х 2 + х – 2 = 0,

Вывод: Какой способ решения такого типа уравнений необходимо применить? Почему?

2.1. Объяснение нового материала.

Решите уравнение: ,

,

Пусть ,

,

, ,

, ,

2.2. Поэтапное закрепление.

№ 6.21(а,в). Решите уравнения.

а) ,

,

Пусть ,

,

, ,

, х₂ = 1. Ответ: ; 1.

в) ,

Пусть ,

,

t ₁ = — 1 – не удовлетворяет условию замены,

,

Вывод: Какой способ решения такого типа уравнений необходимо примен Вывод: Какой способ решения такого типа уравнений необходимо применить? Почему?ить? Почему?

3.1. Объяснение нового материала.

Решите уравнение: ,

,

,

,

,

,

,

, ,

,

3.2. Поэтапное закрепление.

№ 6.19(а,в). Решите уравнения.

а) ,

,

,

Пусть ,

,

, ,

,

t ₁ = . t ₂ = 3.

,

,

,

, , то корней нет.

,

,

,

в) ,

,

,

Пусть ,

,

t ₁ = 1. t ₂ = -1,5 – не удовлетворяет условию замены.

,

,

, ,

,

Вывод: Какой способ решения такого типа уравнений необходимо применить? Почему?

4.1. Объяснение нового материала.

Решите уравнение: ,

,

,

Пусть ,

, ОДЗ: t  0,

,

, ,

, ,

4.2. Поэтапное закрепление.

№ 6.23(б). Решите уравнения.

б) ,

,

Пусть ,

, ОДЗ: t  0,

,

, ,

, х = 1. Ответ: ; 1.

Вывод: Какой способ решения такого типа уравнений необходимо применить? Почему?

5.1. Объяснение нового материала.

Решите уравнение: ,

Пусть

, ОДЗ: t  -2; 3,

,

,

,

у₁ = 1, то t ₁ = ,

, ,

, х – 2 = 1,

Вывод: Какой способ решения такого типа уравнений необходимо применить? Почему?

Подведение итогов урока.

Домашнее задание. § 6.3 (выучить теорию). № 6.17(кроме д), 6.19(б), 6.21(б,г,е), 6.23(а,в), 6.24(а).

Краткое описание документа:

Конспект к третьему уроку по алгебре и началам математического анализа в 10 классе на тему «Уравнения, сводящиеся к простейшим заменой неизвестного» (к учебнику Никольского С.М. и др.).

Образовательная цель: Сформировать навыки решения показательных уравнений способом приведения к одинаковому основанию и уравнений, сводящимся к простейшим заменной неизвестного.

Урок составлен таким образом, чтобы после каждого этапа объяснения материала, учащиеся имели возможность его закреплять и сделать обоснованный вывод о способах решения того или иного типов показательного уравнения.

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 274 человека из 66 регионов

Курс повышения квалификации

Особенности подготовки к проведению ВПР в рамках мониторинга качества образования обучающихся по учебному предмету «Математика» в условиях реализации ФГОС ООО

• Сейчас обучается 100 человек из 37 регионов

Курс повышения квалификации

Авторская разработка онлайн-курса

• Сейчас обучается 90 человек из 41 региона

«Обзор традиционных и современных методик для формирования навыков арифметических вычислений в уме у младших школьников»

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Видео:ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 858 931 материал в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 12.05.2015
• 776
• 0

• 12.05.2015
• 4571
• 0

• 12.05.2015
• 21597
• 352

• 12.05.2015
• 802
• 0

• 12.05.2015
• 2606
• 16

• 12.05.2015
• 519
• 0

• 12.05.2015
• 1210
• 0

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 12.05.2015 9806
• DOCX 247.5 кбайт
• 464 скачивания
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Ковалева Светлана Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 5 месяцев
• Подписчики: 4
• Всего просмотров: 719829
• Всего материалов: 144

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Показательные уравнения. 11 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

«Система работы учителя при подготовке к ЕГЭ по русскому языку»

«Инвестиции в знания всегда дают наибольшую прибыль»

«Современный репетитор: Instagram и новые форматы уроков»

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Тысячи учителей в Австралии вышли на забастовку

Время чтения: 2 минуты

Минобрнауки выделило более 590 тысяч бюджетных мест на 2023-24 учебный год

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Это просто! Как решать Показательные Неравенства?Скачать

Решение тригонометрических уравнений. 10-й класс

Разделы: Математика

Класс: 10

Тип урока: изучение новой темы

Оборудование: экран; мультимедийный проектор; ноутбук, компьютеры. У учащихся на партах листы учета знаний.

Подробное описание хода урока:

Цели урока:

• Систематизация знаний по данной теме, закрепление навыков решения различных тригонометрических уравнений.
• Развитие навыка применять знания в новых ситуациях. Развитие творческого математического мышления.

Задачи урока:

• Повторить решения простейших тригонометрических уравнений, рассмотреть решение уравнений, сводящихся к простейшим заменой неизвестного
• Развивать коммуникативные навыки (работа в группе, самоконтроль, взаимоконтроль).
• Воспитывать самостоятельность, ответственность, творческое отношение к деятельности

Методы обучения: частично-поисковый, проверка уровня знаний, работа по обобщающей схеме, решение познавательных обобщающих задач, системные обобщения, самопроверка, восприятие нового материала, взаимопроверка.

Формы организации урока: индивидуальная, фронтальная.

Оборудование и источники информации: Экран; мультимедийный проектор; ноутбук, компьютеры. У учащихся на партах листы учета знаний.

I. Организационный этап (2 мин.)

1. Приветствие, фиксация отсутствующих
2. Проверка подготовленности уч-ся к уроку и кабинета
3. Организация внимания школьников
4. Тема и цели урока.

II. Этап повторения (10 мин.)

Мышление начинается с удивления.

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников (trigwnon – треугольник, а metrew – измеряю).
Тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

А) Про какую функцию идёт речь.

1) Привычное слово кудлатой наседки
Поставьте на первое место:

2) На месте втором посмотрите-ка – нота.
Важна для любого оркестра

3) На третьем одна одинокая буква,
пятнадцатая в алфавите

4) Один из волос на мордашке котенка
На месте четвертом прочтитеОтвет: косинус.

Б) А что здесь зашифровано?

1) Что кружится, что ложится
И на землю, и на крыши
И о чем поэт зимою
По ночам поэмы пишет?
Это первое словечко.

2) А второе просто «на»

3) Ну, а третье? Угадайте,
Что бежит по проводам?
Напиши, что получилось
И прочти наоборот
Не запутайся, читая,
Слово задом наперед.

Ответ: (снег на ток – котангенс)

Учащиеся разделены на две группы. Представители первой группы выполняют М-Тест. (Приложение 1)

Представители второй группы:

(Работа у доски один учащийся) устанавливают соответствие между уравнениями и корнями.

Найти ошибку. (Работает самостоятельно второй учащийся, готовится на месте)

Цель: повторение понятий арксинус, арккосинус, арктангенс и арккотангенс числа.

III. Этап усвоения новых знаний и способов действий

На слайдах записаны поэтапные решения уравнений (Презентация)

1. Решить уравнения (25 мин.)

Ответ:

б)


Ответ:

Ответ:

2x = t

Ответ:

Ответ: ;

t = – 1 и


Ответ:

IV. Домашнее задание (2 мин.)

1. п.11.2, №11.8 (2 столбик)
2. Выполнить №11.8(1 столбик) работа в парах

V. Итоги урока (3 мин.)

Алгоритм работы с «М-тестом»

1. М-Тест Тестирование
2. Сервер
3. Тест по алгебре 10 кл. Тригонометрия. Зачётный.
4. Зарегистрироваться
5. Начать тестироваться

🎦 Видео

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Показательные уравнения. Видеоурок 11. Алгебра 10 классСкачать

Решение уравнений, сводящихся к простейшим заменой неизвестногоСкачать

10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

решение уравнений, сводящихся к простейшим, заменой неизвестного №2Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Решение уравнения методом замены переменнойСкачать

Уравнения, сводящиеся к квадратным. Видеоурок 31. Алгебра 10 классСкачать