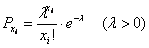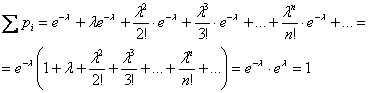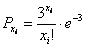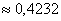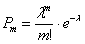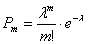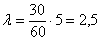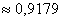Содержание:
Предположим, что мы хотим вычислить вероятность 
появления события 
при большом числе испытаний 
например, 
По формуле Бернулли (2.1) . 
Ясно, что в этом случае непосредственное вычисление по формуле Бернулли технически сложно, тем более если учесть, что сами 
— числа дробные. Поэтому возникает естественное желание иметь более простые приближенные формулы для вычисления 
при больших 
- Такие формулы, называемые асимптотическими, существуют и определяются теоремой Пуассона, локальной и интегральной теоремами Муавра—Лапласа. Наиболее простой из них является теорема Пуассона.
Теорема. Если вероятность 
наступления события 
в каждом испытании стремится к нулю 
при неограниченном увеличении числа 
испытаний 
причем произведение 
стремится к постоянному числу 
то вероятность 
того,
что событие 
появится 
раз в 
независимых испытаниях, удовлетворяет предельному равенству
По этой ссылке вы найдёте полный курс лекций по высшей математике:
По формуле Бернулли (2.1)
или, учитывая, что 
т.е. при достаточно больших 
Так как 
то 
Строго говоря, условие теоремы Пуассона 
при 
так что 
противоречит исходной предпосылке схемы испытаний Бернулли, согласно которой вероятность наступления события в каждом испытании 
Возможно вам будут полезны данные страницы:
Однако, если вероятность 
— постоянна и мала, число испытаний 
— велико и число 
— незначительно (будем полагать, что 
то из предельного равенства (2.5) вытекает приближенная формула Пуассона:
В табл. III приложений приведены значения функции Пуассона 
Примеры с решением
Пример 2.4.
На факультете насчитывается 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета?
Решение:
Вероятность того, что день рождения студента 1 сентября, равна 
Так как 
— мала, 
1825 — велико и 
то применяем формулу Пуассона (2.6):
(по табл. III приложений).
В этом подразделе вы научитесь решать задачи по определению вероятностей редких явлений по формуле Пуассона.
Если в каждом отдельном независимом испытании вероятность одного из событий 
или 
близка к нулю, то события называют редкими. Редкими можно считать события: появление ошибки на некоторой странице в книге, телефонный звонок в квартиру за сутки, количество осадков, выпавших за июнь в городе 
и др.
Для определения вероятности таких явлений применяется асимптотическая формула Пуассона, названная по имени французского математика С. Пуассона, 
Теорема 1.8. Если вероятность 
события 
в каждом повторном испытании связана с числом независимых испытаний 
которое достаточно велико, то вероятность того, что в 
независимых испытаниях событие 
произойдет 
раз, приближенно находится по формуле
Доказательство. По формуле Бернулли имеем:
Выразим 
через 
Так как 
Тогда формула примет вид 
Найдем приближенное значение вероятности при 
помощью предела: 
При выводе формулы использован второй замечательный предел:
Пределы остальных двучленов равны единице при 
Итак, закон Пуассона применяется для определения вероятности появления 
событий, происходящих независимо друг от друга с постоянной вероятностью (средней интенсивностью), причем число испытаний 
достаточно велико 
а вероятность появления события в каждом испытании 
мала, т.е. 
(или 
Приближенные значения вероятности по формуле Пуассона приведены в табл. П. 1.
Задача с решением
Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,002. Найти вероятность того, что в течение 1 мин обрыв произойдет более чем на трех веретенах.
Решение:
По условию задачи 
Так как обрыв нити на каждом веретене может либо произойти, либо не произойти, то речь идет о независимых повторных испытаниях. Тот факт, что вероятность обрыва нити мала, дает возможность использовать для решения формулу Пуассона для редких явлений.
Имеем 
Тогда 
Используя формулу Пуассона, имеем:
Задача 1.63.
Радиоаппаратура состоит из 1000 электроэлементов. Вероятность отказа одного из них в течение года работы равна 0,001 и не зависит от состояния других элементов. Какова вероятность отказа:
а) двух элементов;
б) не менее двух и не более четырех элементов;
в) не менее двух элементов в год?
Решение:
Независимые повторные испытания при 
вычисляют по формуле Пуассона для редких явлений. Тогда 
Найдем вероятность по табл. П. 1.
Задача 1.64.
получает в среднем 300 вызовов в час. Какова вероятность того, что в указанную минуту будут два вызова?
Решение:
Количество вызовов в среднем можно найти, если вычислить число вызовов в минуту, т.е. 
Найдем
Задача 1.65.
Вероятность выхода из строя кодового замка в течение месяца равна 2 %. Какова вероятность того, что в партии из 600 кодовых замков, установленных фирмой на входных дверях домов, 20 замков выйдут из строя в течение месяца?
Решение:
По условию 
Если применять формулу Бернулли, 
то подсчет вероятности будет весьма сложен.
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Формула Бернулли. Формула ПуассонаСкачать
Уравнение Пуассона и математическая постановка задач электростатики
Существует большое количество случаев, когда самым удобным методом нахождения напряженности поля считается решение дифференциального уравнения для потенциала. После его получения применим в качестве основы теорему Остроградского-Гаусса в дифференциальной форме:
где ρ является плотностью распределения заряда, ε 0 — электрической постоянной, d i v E → = ∇ → E → = ∂ E x ∂ x + ∂ E y ∂ y + ∂ E z ∂ z — дивергенцией вектора напряженности и выражением, связывающим напряженность поля и потенциал.
Произведем подстановку ( 2 ) в ( 1 ) :
Учитывая, что d i v g r a d φ = ∇ 2 φ = ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 + ∂ 2 φ ∂ z 2 , где ∆ = ∇ 2 — это оператор Лапласа, равенство ( 3 ) принимает вид:
Выражение ( 4 ) получило название уравнения Пуассона для вакуума. При отсутствующих зарядах запишется как уравнение Лапласа:
После нахождения потенциала переходим к вычислению напряженности, используя ( 2 ) . Решения уравнения Пуассона должны удовлетворять требованиям:
- значение потенциала как непрерывная функция;
- потенциал должен быть конечной функцией;
- производные потенциала как функции по координатам должны быть конечными.
При наличии сосредоточенных зарядов в объеме V , решение уравнения ( 4 ) будет выражаться для потенциала вида:
Общая задача электростатики сводится к нахождению решения дифференциального уравнения, то есть уравнения Пуассона, удовлетворяющего вышеперечисленным требованиям. Теоретические вычисления известны для небольшого количества частных случаев. Если возможно подобрать функцию φ , удовлетворяющую условиям, то она является единственным решением.
В таких задачах не всегда необходимо задавать заряды или потенциалы во всем пространстве. Для нахождения электрического поля в полости, окруженной проводящей оболочкой, достаточно вычислить поле тел, находящихся внутри нее.
Любое решение уравнения Пуассона ограниченной области может быть определено краевыми условиями, накладывающимися на поведение решения. Границы перехода из одной среды в другую имеют условия, которые должны быть выполнены:
E 2 n — E 1 n = 4 π σ , или ∂ φ 1 ∂ n — ∂ φ 2 ∂ n = 0 .
где σ — это поверхностная полость свободных зарядов, n – единичный вектор нормали к границе раздела, проведенный из среды 1 в 2 , τ — единичный вектор, касательный к границе.
Эти уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной вектора напряженностей электрического поля при переходе через любую заряженную поверхность независимо от ее формы и наличия или отсутствия зарядов вне ее.
Видео:Формула ПуассонаСкачать
Уравнение Пуассона в сферических, полярных и цилиндрических координатах
Запись уравнения может быть как при помощи декартовых координат, также и сферических, цилиндрических, полярных.
При наличии сферических r , θ , υ уравнение Пуассона запишется как:
1 r 2 · ∂ ∂ r r 2 ∂ φ ∂ r + 1 r 2 sin θ ∂ θ sin θ · ∂ φ ∂ θ + ∂ 2 φ r 2 sin 2 θ ∂ φ 2 = — 1 ε 0 ρ .
В полярных r , θ :
1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ r 2 ∂ θ 2 = — 1 ε 0 ρ .
В цилиндрических r , υ , z :
1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ ∂ z 2 + ∂ 2 φ r 2 ∂ υ 2 = — 1 ε 0 ρ .
Видео:Формула ПуассонаСкачать
Примеры решения задач
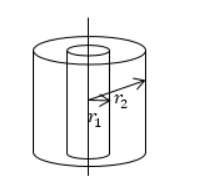
Найти поле между коаксиальными цилиндрами с радиусами r 1 и r 2 и с имеющейся разностью потенциалов ∆ U = φ 1 — φ 2 .
Решение
Необходимо зафиксировать уравнение Лапласа с цилиндрическими координатами, учитывая аксиальную симметрию:
1 r · ∂ ∂ r r ∂ φ ∂ r = 0 .
Решение имеет вид φ = — A ln ( r ) + B . Для этого следует выбрать нулевой потенциал на нужном цилиндре, тогда:
φ ( r 2 ) = 0 = — A ln r 2 + B , следовательно
φ ( r 1 ) = ∆ U = — A ln r 1 + B , получим:
A = ∆ U ln r 2 r 1 .
φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .
Ответ: поле с двумя коаксиальными цилиндрами может быть задано при помощи функции φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .
Найти потенциал поля, которое создает бесконечно круглый цилиндр с радиусом R и объемной плотностью заряда ρ . Использовать уравнение Пуассона.
Решение
Необходимо направить ось Z по оси цилиндра. Видно, что цилиндрическое распределение заряда аксиально симметрично, потенциал имеет такую же симметрию, иначе говоря, считается функцией φ ( r ) с r , являющимся расстоянием от оси цилиндра. Для решения используется цилиндрическая система координат. Уравнение Пуассона в ней запишется как:
φ 2 = C 2 ln r + C ‘ 2 .
C 1 , C ‘ 1 , C 2 , C ‘ 2 — это постоянные интегрирования. Имеем, что потенциал во всех точках должен быть конечным, а l i m r → 0 ln r = ∞ . Отсюда следует, что C 1 = 0 . Далее необходимо пронормировать потенциал, задействовав условие φ 1 ( 0 ) = 0 . Получим C ‘ 1 = 0 .
Поверхностные заряды отсутствуют, поэтому напряженность электрического поля на поверхности шара является непрерывной. Следовательно, что и производная от потенциала также непрерывна при r = R , как и сам потенциал. Исходя из условий, можно найти C 2 , C ‘ 2 :
C 2 ln R + C ‘ 2 = — 1 4 ρ ε 0 R 2 .
C 2 R = — 1 2 ρ ε 0 R .
Значит, полученные выражения записываются как:
Ответ: потенциал поля равняется:
Видео:Математика без Ху!ни. Теория вероятностей. Схема БернуллиСкачать
2.3.3. Распределение Пуассона
Случайная величина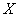 
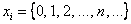
, распределённая по этому закону, принимает бесконечное и счётное количество значений 
, вероятности появления которых определяются формулой:
Или, если расписать подробно: 
Вспоминая разложение экспоненты в ряд, легко убедиться, что: 
Математическое ожидание пуассоновской случайной величины равно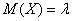 
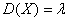
и дисперсия – тому же самому значению: 
.
Во всех задачах параграфа Формула Пуассона мы лишь ПОЛЬЗОВАЛИСЬ распределением Пуассона для приближенного расчёта вероятностей, в то время как ТОЧНЫЕ значения следовало находить по формуле Бернулли, т.е., там имело место биномиальное распределение. И последующие задачи отличаются принципиально –
– отличие состоит в том, что сейчас речь идёт именно о РАСПРЕДЕЛЕНИИ Пуассона:
Задача 99
Случайная величина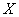 
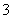
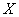
подчинена закону Пуассона с математическим ожиданием, равным 
. Найти вероятность того, что данная случайная величина 
примет значение, меньшее, чем её математическое ожидание.
Решение: известно, что математическое ожидание распределения Пуассона в точности равно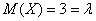 
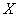
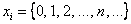
, таким образом, случайная величина 
принимает значения 
с вероятностями: 
Интересующее нас событие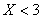 
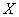
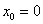
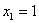
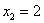
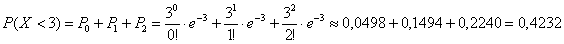
состоит в трёх несовместных исходах: случайная величина 
примет значение 
или 
, или 
. По теореме сложения вероятностей несовместных событий:
– вероятность того, что случайная величина 
примет значение, меньшее, чем ее математическое ожидание.
Ответ: 
Аналогичная задача на понимание:
Задача 100
Случайная величина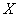 
подчинена закону Пуассона с единичным математическим ожиданием. Найти вероятность того, что данная случайная величина примет положительное значение.
Решение и ответ в конце книги.
Помимо прочего, распределение Пуассона нашло широкое применение в теории массового обслуживания для вероятностной характеристики простейшего потока событий. Постараюсь быть лаконичным:
Пусть в некоторую систему поступают заявки (телефонные звонки, приходящие клиенты и т.д.). Поток заявок называют простейшим, если он удовлетворяет условиям стационарности, отсутствия последствий и ординарности.
Стационарность подразумевает то, что интенсивность заявок постоянна и не зависит от времени суток, дня недели или других временнЫх рамок. Иными словами, не бывает «часа пик» и не бывает «мёртвых часов». Отсутствие последствий означает, что вероятность появления новых заявок не зависит от «предыстории», т.е. нет такого, что «одна бабка рассказала» и другие «набежали» (или наоборот, разбежались). И, наконец, свойство ординарности характеризуется тем, что за достаточно малый промежуток времени практически невероятно появление двух или бОльшего количества заявок. «Две старушки в дверь?» – нет уж, увольте, рубить удобнее по порядку.
Итак, пусть в некоторую систему поступает простейший поток заявок со средней интенсивностью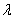 
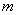
заявок в некоторую единицу времени (минуту, час, день или в любой другой). Тогда вероятность того, что за данный промежуток времени, в систему поступит ровно 
заявок, равна:
Поразительно, с какой скоростью устаревают задачи:
Задача 101
Звонки в диспетчерскую такси представляет собой простейший пуассоновский поток со средней интенсивностью 30 вызовов в час. Найти вероятность того, что: а) за 1 мин. поступит 2-3 вызова, б) в течение пяти минут будет хотя бы один звонок.
Решение: используем формулу Пуассона: 
а) Учитывая стационарность потока, вычислим среднее количество вызовов за 1 минуту:
вызова – в среднем за одну минуту.
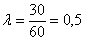
По теореме сложения вероятностей несовместных событий:
– вероятность того, что за 1 минуту в диспетчерскую поступит 2-3 вызова.
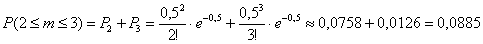
б) Вычислим среднее количество вызов за пять минут: 
По формуле Пуассона:
– вероятность того, что в течение 5 минут не будет ни одного звонка.
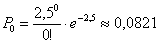
По теореме сложения вероятностей противоположных событий:
– вероятность того, что в течение 5 минут будет хотя бы один вызов.
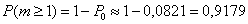
Ответ: а)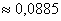 
, б) 
Обращаю внимание, что в отличие от задач параграфа Формула Пуассона, эту задачу уже нельзя решить по формуле Бернулли. По той причине, что заранее не известно общее количество исходов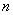 
(точное количество звонков в тот или иной час).
И предсказать это значение, разумеется, невозможно.
Для самостоятельного решения:
Задача 102
Среднее число автомобилей, проходящих таможенный досмотр в течение часа, равно 3. Найти вероятность того, что: а) за 2 часа пройдут досмотр от 7 до 10 автомобилей; б) за пол часа успеет пройти досмотр только 1 автомобиль.
Таможня пройдена, достаём припрятанное:
Полную и свежую версию этой книги в pdf-формате ,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
🎥 Видео
Задача №7 теория вероятностей контрольная работа Формула ПуассонаСкачать
Теорема Пуассона | Распределение Пуассона | Теория вероятностейСкачать
Приближенная формула Пуассона: примеры задач и расчеты в ExcelСкачать
Теория вероятностей #8: формула Бернулли и примеры ее использования при решении задачСкачать
Формула БернуллиСкачать
Закон Пуассона распределения случайной величиныСкачать
7.2 Задача 1. Краевая задача для уравнения ПуассонаСкачать
Адиабатный процесс. 10 класс.Скачать
9. Уравнение ПуассонаСкачать
29. Адиабатический процесс. Уравнение ПуассонаСкачать
Математика без Ху!ни. Сложение и умножение вероятностей. Формула полной вероятности.Скачать
Локальная формула Муавра-ЛапласаСкачать
