Уравнение динамического звена по передаточной функции (6 видео)

Уравнение динамического звена по передаточной функции

Понятие линейного динамического звена

САУ удобно представлять для анализа и при синтезе в виде взаимосвязанной совокупности отдельных элементов динамических звеньев.

Под динамическим звеном понимают в общем случае абстрактное устройство, имеющее вход и выход, и для которого задано уравнение, связывающее сигналы на входе и выходе, как это показано на рис. 1.

Подробное изучение свойств реальных объектов управления и систем автоматического управления приводит к описанию динамических звеньев в виде нелинейных дифференциальных уравнений. Но во многих случаях их можно линеаризовать, то есть заменить нелинейные уравнения линейными, приближенно описывающими процессы в системах. Тем самым осуществляется декомпозиция задач анализа и синтеза систем, то есть первоначально используют линейное представление, а затем осуществляют учет вносимых нелинейностями особенностей. Такому подходу способствует то, что, в большинстве случаев, нормально функционирующая система работает в режиме малых отклонений, при которых нелинейности не проявляются. В дальнейшем мы будем рассматривать преимущественно аппарат изучения линейных систем, а особенности систем других классов: нелинейных, импульсных, цифровых и стохастических, будут излагаться позднее в других учебных дисциплинах.

Если уравнение, связывающее сигналы и , линейно, то говорят о линейном динамическом звене

Уравнение линейного динамического звена имеет следующий общий вид:

где — постоянные коэффициенты, .

Использовать такое описание динамического звена в задачах анализа и синтеза систем и объектов управления не рационально, поэтому существуют и иные формы описания и представления динамических звеньев и систем в целом.

Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу

Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов

Преобразуем уравнение (2) к следующему виду

Получим из (3) отношение изображений выходного и входного сигналов

Отношение (4) не зависит от изображений сигналов, определяется только параметрами самого динамического звена (), имеет вид дробно-рациональной функции.

Отношение изображений выходного и входного сигналов называют передаточной функцией динамического звена

называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции это характеристический полином дифференциального уравнения, описывающего динамическое звено.

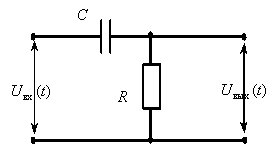
Определим передаточную функцию динамического звена по его принципиальной электрической схеме

По второму закону Кирхгоффа запишем уравнения описывающие схему

С учетом того, что

Получим операторные уравнения

Из второго уравнения выразим значение изображения тока

Подставим полученное выражение в первое уравнение системы

В итоге получаем искомую передаточную функцию

Графически передаточные функции динамического звена представляют в следующем виде:

Если известно изображение входного сигнала и передаточная функция динамического звена, всегда можно найти изображение выходного сигнала при нулевых начальных условиях

.(5)

В общем случае САУ состоит из множества динамических звеньев, сигналы с выходов звеньев могут суммироваться или вычитаться, суммироваться с внешними для САУ сигналами. Суммирование и вычитание изображений сигналов могут быть представлено графически с помощью суммирующих звеньев:

Показанная выше неоднозначность графического представления вычитания изображений на суммирующем элементе связана с различием в стандартах разных стран.

Используя графическое представление передаточных функций звеньев и суммирующие звенья, можно в графической форме представить операторные уравнения, описывающие САУ. Такое графическое представление операторных уравнений в ТАУ называют структурной схемой.

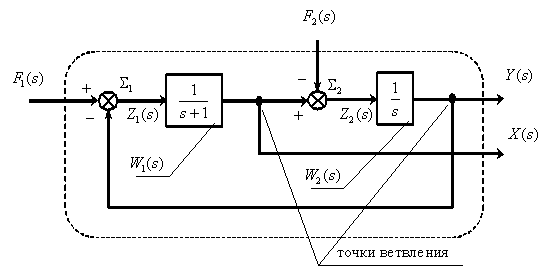
По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.

Получим систему операторных уравнений, подвергнув исходную систему дифференциальных уравнений преобразованию Лапласа и заменив оригиналы изображениями,

Из первого уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим

Тогда передаточная функция этого звена имеет вид

а выражение описывает суммирующее звено . Таким образом, получены два фрагмента структурной схемы

Из второго уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим, вводя обозначение,

Тогда передаточная функция этого звена имеет вид

а выражение описывает суммирующее звено . Таким образом, получены еще два фрагмента структурной схемы

Соединим все фрагменты структурной схемы объекта управления, объединяя одноименные сигналы, либо разветвляя их с помощью точек ветвления , показанных на схеме. В результате получим

Временные характеристики динамического звена

Временной или импульсной характеристикой динамического звена называют реакцию звена на , обозначая ее как . При этом схема эксперимента имеет вид

Выясним, что представляет собой временная характеристика, то есть почему ее называют характеристикой динамического звена?

Для этого рассмотрим динамическое звено с передаточной функцией

В этом случае, в соответствии с (5), имеем

Получаем, что передаточная функция звена это изображение по Лапласу импульсной характеристики динамического звена. В свою очередь, импульсная характеристика может быть определена по передаточной функции

при использовании разложения в форму Хэвисайта и обратное преобразование Лапласа.

Знание импульсной характеристики позволяет определить реакцию динамического звена на сигнал любой формы.

Для динамического звена с передаточной функцией преобразуем (5), используя теорему об умножении изображений преобразования Лапласа,

а если легко получить , тогда

Переходной характеристикой или переходной функцией динамического звена называют реакцию динамического звена на , обозначая ее как . При этом схема эксперимента имеет вид

Для анализа переходной характеристики рассмотрим динамическое звено с передаточной функцией

В этом случае, в соответствии с (5), имеем

По теореме об интегрировании оригинала имеем

Переходная функция является интегралом по времени от импульсной характеристике и наоборот

Переходная характеристика динамического звена может быть определена по передаточной функции

Контрольные вопросы и задачи

Что такое линейное динамическое звено?

Как определить передаточную функцию линейного динамического звена?

Перечислите основные элементы структурных схем систем управления.

Как определить по передаточной функции динамического звена его временные характеристики: импульсную и переходную?

Как по переходной характеристике определить импульсную характеристику динамического звена?

Определите передаточную функцию динамического звена по его принципиальной электрической схеме

Содержание

Лекция №3. Динамические звенья и их характеристики
Лекция №3. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ
3.1. Общие положения
Уравнение динамического звена по передаточной функции
📸 Видео

Видео:Теория автоматического управления. Лекция 7. Типовые звенья САУСкачать

Лекция №3. Динамические звенья и их характеристики

Видео:Типовые динамические звенья | Вечер с теорией управления, вебинар 3Скачать

Лекция №3. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ

Видео:10) ТАУ для чайников Части 4.1. и 4.2. Типовые динамические звенья. Усилитель. Апериодическое звено.Скачать

3.1. Общие положения

Для создания общей методики расчета различных систем автоматического регулирования удобно ввести понятие динамического звена. Под динамическим звеном понимают устройство любого физического вида и конструктивного содержания, описываемое определённым дифференциальным уравнением.

В соответствии с этим классификация звеньев производится именно по виду дифференциального уравнения. Одним и тем же уравнением могут описываться весьма разнообразные устройства (механические, электрические, гидравлические и т. д.). Для ТАУ это будет один и тот же тип звена.

Обозначим входную величину звена через х1, выходную – через х2, а возмущающее воздействие – через DF (рис. 2.2).

Статическая характеристика любого звена может быть изображена в виде прямой линии (рис. 3.1), так как пока рассмотрим только линейные, или точнее линеаризованные системы.

В звеньях позиционного или статического типа линейной зависимостью х2 = k х1 связаны выходная и входная величины в установившемся режиме (рис. 3.1, а). Коэффициент пропорциональности между выходной и входной величинами представляет собой коэффициент передачи.

Рис. 3.1. Характеристики позиционных звеньев

В звеньях интегрирующего типа линейной зависимостью связаны производная выходной величины и входная величина в установившемся режиме (рис. 3.1, б). В этом случае для установившегося режима будет справедливым равенство , откуда и произошло название этого типа звеньев. Коэффициент пропорциональности k называется коэффициентом передачи звена. В случае, если входная и выходная величины звена имеют одинаковую размерность, коэффициенту передачи соответствует размерность – секунда в минус первой степени (с-1).

В звеньях дифференцирующего типа, в установившемся режиме, линейной зависимостью связаны выходная величина и производная входной (рис. 3.1, в), откуда и произошло название этого типа звеньев. Коэффициент пропорциональности называется коэффициентом передачи звена. Если входная и выходная величины имеют одинаковую размерность, коэффициенту передачи соответствует размерность – секунда (с).

Как уже отмечалось, классификация звеньев производится по виду дифференциального уравнения или, что все равно, по виду передаточной функции звена. Предположим, что звено, изображенное на рис. 2.1, описывается дифференциальным уравнением, представленным в стандартной форме записи

. (3.1)

При нулевых начальных условиях (то есть при t

Видео:[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать

Уравнение динамического звена по передаточной функции

3.1. Динамический режим САУ.
Уравнение динамики

Установившийся режим не является характерным для САУ. Обычно на управляемый процесс действуют различные возмущения, отклоняющие управляемый параметр от заданной величины.

Процесс установления требуемого значения управляемой величины называется регулированием . Ввиду инерционности звеньев регулирование не может осуществляться мгновенно.

Рассмотрим САР, находящуюся в установившемся режиме, характеризующемся значением выходной величины y = y _o . Пусть в момент t = 0 на объект воздействовал какой — либо возмущающий фактор, отклонив значение регулируемой величины. Через некоторое время регулятор вернет САР к первоначальному состоянию (с учетом статической точности) (рис.24). Если регулируемая величина изменяется во времени по апериодическому закону, то процесс регулирования называется апериодическим .

При резких возмущениях возможен колебательный затухающий процесс (рис.25а). Существует и такая вероятность, что после некоторого времени Т _р в системе установятся незатухающие колебания регулируемой величины — незатухающий колебательный процесс (рис.25б). Последний вид — расходящийся колебательный процесс (рис.25в).

Таким образом, основным режимом работы САУ считается динамический режим , характеризующийся протеканием в ней переходных процессов . Поэтому второй основной задачей при разработке САУ является анализ динамических режимов работы САУ .

Поведение САУ или любого ее звена в динамических режимах описывается уравнением динамики y(t) = F(u,f,t) , описывающее изменение величин во времени. Как правило, это дифференциальное уравнение или система дифференциальных уравнений. Поэтому основным методом исследования САУ в динамических режимах является метод решения дифференциальных уравнений . Порядок дифференциальных уравнений может быть довольно высоким, то есть зависимостью связаны как сами входные и выходные величины u(t), f(t), y(t) , так и скорости их изменения, ускорения и т.д. Поэтому уравнение динамики в общем виде можно записать так:

F(y, y’, y”. y (n) , u, u’, u”. u (m) , f, f ’, f ”. f (k) ) = 0 .

3.2. Линеаризация уравнения динамики

В общем случае уравнение динамики оказывается нелинейным, так как реальные звенья САУ обычно нелинейны. В целях упрощения теории нелинейные уравнения заменяют линейными, которые приблизительно описывают динамические процессы в САУ. Получаемая при этом точность уравнений оказывается достаточной для технических задач. Процесс преобразования нелинейных уравнений в линейные называется линеаризацией уравнений динамики . Рассмотрим сначала геометрическое обоснование линеаризации.

В нормально функционирующей САУ значение регулируемой и всех промежуточных величин незначительно отличается от требуемых. В пределах малых отклонений все нелинейные зависимости между величинами, входящими уравнение динамики, могут быть приближенно представлены отрезками прямых линий. Например, нелинейная статическая характеристика звена на участке АВ (рис.26) может быть представлена отрезком касательной в точке номинального режима А»В». Начало координат переносится в точку О’, и в уравнениях записываются не абсолютные значения величин y,u,f , а их отклонения от номинальных значений: y = y — y _н , u = u — u _н , f = f — f _н . Это позволяет получить нулевые начальные условия , если считать, что при t 0 система находилась в номинальном режиме в состоянии покоя.

Математическое обоснование линеаризации состоит в том, что если известно значение f(a) какой — либо функции f(x) в любой точке x = a , а также значения производных от этой функции в данной точке f’(a), f”(a), . f (n) (a) , то в любой другой достаточно близкой точке x + x значение функции можно определить, разложив ее в окрестности точки a в ряд Тейлора:

Аналогично можно разложить и функцию нескольких переменных. Для простоты возьмем упрощенный, но наиболее характерный вариант уравнения динамики САУ: F(y,y’,y»,u,u’) = f. Здесь производные по времени u’,y’,y» также являются переменными. В точке, близкой к номинальному режиму: f = f _н + f и F = F _н + F . Разложим функцию F в ряд Тейлора в окрестности точки номинального режима, отбрасывая члены ряда высоких порядков малости:

В номинальном режиме, когда все отклонения и их производные по времени равны нулю, получаем частное решение уравнения: F н = f н . Учитывая это и вводя обозначения получим:

a _o y” + a ₁ y’ + a ₂ y = b _o u’ + b ₁ u + c _o f .

Отбрасывая все знаки , получим:

a o y” + a 1 y’ + a 2 y = b o u’ + b 1 u + c o f .

Отбрасывая все знаки , получим:

В более общем случае:

a _o y (n) + a ₁ y (n-1) + . + a _{n — 1} y’ + a _n y = b _o u (m) + . + b _m — 1u’ + b _m u + c o f.

При этом всегда нужно помнить, что в данном уравнении используются не абсолютные значения величин y, u, f их производных по времени, а отклонения этих величин от номинальных значений. Поэтому полученное уравнение будем называть уравнением в отклонениях .

К линеаризованной САУ можно применить принцип суперпозиции : реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет звено с двумя входами u и f разложить на два звена, каждое из которых имеет один вход и один выход (рис.27). Поэтому в дальнейшем мы ограничимся изучением поведения систем и звеньев с одним входом, уравнение динамики которых имеет вид:

a o y (n) + a 1 y (n-1) + . + a n — 1 y’ + a n y = b o u (m) + . + b m — 1u’ + b m u.

Это уравнение описывает САУ в динамическом режиме лишь приближенно с той точностью, которую дает линеаризация. Однако следует помнить, что линеаризация возможна только при достаточно малых отклонениях величин и при отсутствии разрывов в функции F в окрестностях интересующей нас точки, которые могут быть созданы различными выключателями, реле и т.п.

Обычно n m , так как при n САУ технически нереализуемы.

3.3. Передаточная функция

В ТАУ часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператора p = d/dt так, что, dy/dt = py , а p n = d n /dt n . Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p . В операторной форме исходное дифференциальное уравнение записывается как алгебраическое:

a o p (n) y + a 1 p (n-1) y + . + a n y = (a o p (n) + a 1 p (n-1) + . + a n )y = (b o p (m) + b 1 p (m-1) + . + b m )u

Не надо путать эту форму записи с операционным исчислением хотя бы потому, что здесь используются непосредственно функции времени y(t), u(t) ( оригиналы ), а не их изображения Y(p), U(p) , получаемые из оригиналов по формуле преобразования Лапласа. Вместе с тем при нулевых начальных условиях с точностью до обозначений записи действительно очень похожи. Это сходство лежит в природе дифференциальных уравнений. Поэтому некоторые правила операционного исчисления применимы к операторной форме записи уравнения динамики. Так оператор p можно рассматривать в качестве сомножителя без права перестановки, то есть pyyp . Его можно выносить за скобки и т.п.

Поэтому уравнение динамики можно записать также в виде:

Дифференциальный оператор W(p) называют передаточной функцией . Она определяет отношение выходной величины звена к входной в каждый момент времени: W(p) = y(t)/u(t) , поэтому ее еще называют динамическим коэффициентом усиления . В установившемся режиме d/dt = 0 , то есть p = 0 , поэтому передаточная функция превращается в коэффициент передачи звена K = b _m /a _n .

Знаменатель передаточной функции D(p) = a _o p n + a ₁ p n — 1 + a ₂ p n — 2 + . + a _n называют характеристическим полиномом . Его корни, то есть значения p, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функции .

Числитель K(p) = b o p m + b 1 p m — 1 + . + b m называют операторным коэффициентом передачи . Его корни, при которых K(p) = 0 и W(p) = 0 , называются нулями передаточной функции .

Звено САУ с известной передаточной функцией называется динамическим звеном . Оно изображается прямоугольником, внутри которого записывается выражение передаточной функции. То есть это обычное функциональное звено, функция которого задана математической зависимостью выходной величины от входной в динамическом режиме. Для звена с двумя входами и одним выходом должны быть записаны две передаточные функции по каждому из входов. Передаточная функция является основной характеристикой звена в динамическом режиме, из которой можно получить все остальные характеристики. Она определяется только параметрами системы и не зависит от входных и выходных величин. Например, одним из динамических звеньев является интегратор. Его передаточная функция W _и (p) = 1/p . Схема САУ, составленная из динамических звеньев, называется структурной .

3.4. Элементарные динамические звенья

Динамика большинства функциональных элементов САУ независимо от исполнения может быть описана одинаковыми по форме дифференциальными уравнениями не более второго порядка. Такие элементы называют элементарными динамическими звеньями . Передаточная функция элементарного звена в общем виде задается отношением двух полиномов не более чем второй степени:

W_э(p) = .

Известно также, что любой полином произвольного порядка можно разложить на простые сомножители не более, чем второго порядка. Так по теореме Виета можно записать

D(p) = a _o p n + a ₁ p n — 1 + a ₂ p n — 2 + . + a _n = a _o (p — p ₁ )(p — p 2 ). (p — p n ),

где p 1 , p 2 , . p n — корни полинома D(p) . Аналогично

K(p) = b o p m + b 1 p m — 1 + . + b m = b o (p — p

m — корни полинома K(p) . То есть

Корни любого полинома могут быть либо вещественными p _i = a _i , либо комплексными попарно сопряженными p _i = a _i ± j _i . Любому вещественному корню при разложении полинома соответствует сомножитель (p — a _i ) . Любая пара комплексно сопряженных корней соответствует полиному второй степени, так как

(p — a _i + j _i )(p — a _i — j _i ) = (p — ai) 2 + _i 2 = p 2 — 2pa _i + (a _i 2 + _i 2 ).

Поэтому любую сложную передаточную функцию линеаризованной САУ можно представить как произведение передаточных функций элементарных звеньев. Каждому такому звену в реальной САУ, как правило, соответствует какой — то отдельный узел. Зная свойства отдельных звеньев можно судить о динамики САУ в целом.

В теории удобно ограничиться рассмотрением типовых звеньев , передаточные функции которых имеют числитель или знаменатель, равный единице, то есть W(p) = , W(p) = , W(p) = 1/p , W(p) = p , W(p) = Tp + 1 , W(p) = k . Из них могут быть образованы все остальные звенья. Звенья, у которых порядок полинома числителя больше порядка полинома знаменателя, технически нереализуемы.

Какой режим САУ называется динамическим?
Что называется регулированием?
Назовите возможные виды переходных процессов в САУ. Какие из них являются допустимыми для нормальной работы САУ?
Что называется уравнением динамики? Каков его вид?
Как провести теоретическое исследование динамики САУ?
Что называется линеаризацией?
В чем геометрический смысл линеаризации?
В чем состоит математическое обоснование линеаризации?
Почему уравнение динамики САУ называется уравнением в отклонениях?
Справедлив ли для уравнения динамики САУ принцип суперпозиции? Почему?
Как звено с двумя и более входами представить схемой, состоящей из звеньев с одним входом?
Запишите линеаризованное уравнение динамики в обычной и в операторной формах?
В чем смысл и какими свойствами обладает дифференциальный оператор p?
Что называется передаточной функцией звена?
Запишите линеаризованное уравнение динамики с использованием передаточной функции. Справедлива ли эта запись при ненулевых начальных условиях? Почему?
Напишите выражение для передаточной функции звена по известному линеаризованному уравнению динамики: (0.1p + 1)py(t) = 100u(t).
Что называется динамическим коэффициентом усиления звена?
Что называется характеристическим полиномом звена?
Что называется нулями и полюсами передаточной функции?
Что называется динамическим звеном?
Что называется структурной схемой САУ?
Что называется элементарными и типовыми динамическими звеньями?
Как сложную передаточную функцию разложить на передаточные функции типовых звеньев?