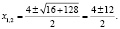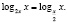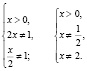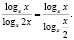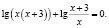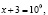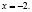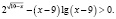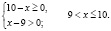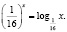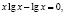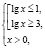Задание «Проблемы, типичные ошибки учащихся»
Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики порой не могут объяснить, чем вызваны эти ошибки.
Решая уравнения и неравенства учащиеся допускают типичные ошибки:
· Незнание правил, определений, формул.
· Непонимание правил, определений, формул.
· Неумение применять правила, определения, формулы.
· Неверное применение формул.
· Невнимательное чтение условия и вопроса задания.
· Раскрытие скобок и применение формул сокращенного умножения.
Какие же проблемы, трудности общего характера возникают у учащихся при изучении математики ( их несомненно можно отнести и к трудностям, которые возникают у уч-ся при изучении темы «Уравнения и неравенства»):
· Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
· Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
· Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
· Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам . Учащиеся не всегда сами понимают, что именно они написали.
· Усталость . Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
· Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
· Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
· Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.
Ошибки, допускаемые обучающимися при решении уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
Предлагаю на конкретных примерах рассмотреть ошибки подобного рода и определить способы их предупреждения и исправления, но прежде всего хочу обратить внимание на следующую мысль: не надо бояться приобрести посторонние корни, их можно отбросить путем проверки ,надо бояться потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим образом.
log3(5 – x) = 3 – log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)( –1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x – 32 = 0,
Учащиеся часто, не проводя дополнительных рассуждений, записывают оба числа в ответ. Но как показывает проверка, число x = 8 не является корнем исходного уравнения, так как при x = 8 левая и правая части уравнения теряют смысл. Проверка показывает, что число x = –4 является корнем заданного уравнения.
б) Решить уравнение
Область определения исходного уравнения задается системой
Для решения заданного уравнения перейдем к логарифму по основанию x, получим
Мы видим, что левая и правая части этого последнего уравнения при x = 1 не определены, но это число является корнем исходного уравнения (убедиться в этом можно путем непосредственной подстановки). Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня x = 1, следует указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами. Хочу подтвердить сказанное следующим примером.
Ученик предлагает следующее ошибочное решение этого уравнения:
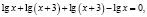
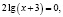
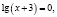
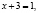
Поверка показывает, что х = –2 не является корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не имеет.
Однако это не так. Выполнив подстановку х = –4 в заданное уравнение, мы можем убедиться, что это корень.
Предлагаю проанализировать, почему произошла потеря корня.
В исходном уравнении выражения х и х + 3 могут быть одновременно оба отрицательными или оба положительными, но при переходе к уравнению 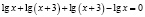
Чтобы избежать потери корня, можно поступить следующим образом: перейти в исходном уравнении от логарифма суммы к логарифму произведения. Возможно в этом случае появление посторонних корней, но от них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем. Предлагаю рассмотреть это на следующем примере.
Попытка решать это неравенство привычными алгоритмическими способами не приведет к ответу. Решение здесь должно состоять в оценке значений каждого слагаемого левой части неравенства на области определения неравенства.
Найдем область определения неравенства:
Для всех x из промежутка (9;10] выражение 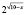
Для всех x из промежутка (9;10] выражение ( x – 9) имеет положительные значения, а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда выражение
– (x – 9) lg(x – 9) положительно или равно нулю.
Окончательно имеем x ∈ (9;10]. Хочу заметить, что при таких значениях переменной каждое слагаемое, стоящее в левой части неравенства, положительно (второе слагаемое может быть равно нулю), а значит их сумма всегда больше нуля. Следовательно, решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением уравнений.
Некоторые учащиеся, решая это уравнение графически (хочу отметить, что его другими элементарными способами решить нельзя), получают лишь один корень (он является абсциссой точки, лежащей на прямой y = x), ибо графики функций
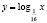
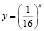
это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из них является абсциссой точки, лежащей на биссектрисе первого координатного угла y = x, другой корень 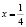
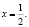
Этот пример удачно иллюстрирует следующий вывод: графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции «разномонотонны» (одна из них возрастает, а другая – убывает), и недостаточно математически корректно в случае одномонотонных функций (обе либо одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Остановлюсь на типичных ошибки такого рода.
а) Решить уравнение x х = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
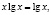
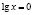
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее произошла потеря двух корней уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
7. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше.Этого делать не следует.
8.Хочу привести пример еще одной ошибки, связанной с решением неравенств.
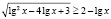
Привожу ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
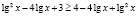
откуда получаем неверное числовое неравенство 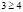
Однако полученный вывод неверен, например, при х = 1000 имеем
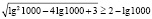
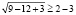
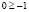
Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Привожу правильное решение. Найдем область определения исходного неравенства. Она задается системой
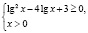
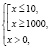
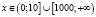
Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а) 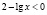
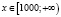
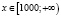
б) 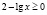
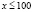
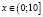
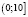
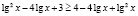
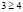
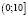
Ответ: 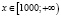
9. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.
Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.
Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.
Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x .
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.
Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
· проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
· проверка правильности решения задач путём составления и решения задач, обратных к данной;
· оценка результата решения задачи с точки зрения здравого смысла;
· проверка аналитического решения графическим способом.
Способы исправления и предупреждения ошибок
Свести ошибки к минимуму способствуют следующие профилактические меры:
- Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
- Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
- При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
- Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
- Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.
- math4school.ru
- Ошибки в уравнениях
- Потеря корней
- Посторонние корни
- Ошибки, связанные с заменой переменной
- Ошибки, связанные с использованием модуля
- Подбор корней без обоснования
- Ошибки в логарифмических и показательных уравнениях
- Ошибки в тригонометрических уравнениях
- Учитель допустил ошибку на доске, а когда дети начали смеяться над ним, объяснил им простую истину…
- 🔍 Видео
Видео:Решение биквадратных уравнений. 8 класс.Скачать

math4school.ru
Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Ошибки в уравнениях
При выполнении контрольных, тестовых и экзаменационных работ по математике учащиеся решают самые разнообразные уравнения, отличающиеся по тематике и по сложности. Разобрать все ошибки, которые при этом допускаются, не представляется возможным. Ниже предлагаются примеры лишь наиболее распространенных ошибок и анализ ситуаций, в которых эти ошибки допускаются.
Потеря корней
При решении уравнений из-за выполнения нетождественных преобразований может произойти либо потеря корней , либо появление посторонних корней .
При выполнении нетождественных преобразований в процессе решения уравнения может произойти сужение области допустимых значений неизвестного , а значит, корни могут оказаться потерянными.
K Упражнение. Решить уравнение lg (x – 10) 2 + lg x 2 = 2lg 24 .
L Неправильное решение.
2lg (x – 10) + 2lg x = 2lg 24,
Произвели проверку и убедились, что все корни удовлетворяют данному уравнению.
Комментарий . Из-за неправильного применения формул произошло сужение области допустимых значений неизвестного.
J Правильное решение.
Ответ: –2; 4; 6 и 12.
При делении обеих частей уравнения на выражение, содержащее неизвестное , могут быть потеряны корни, которые обращают эти выражения в ноль.
K Упражнение 1. Решить уравнение 3 х ( х 2 – 2 х – 3) = 9 ( х 2 – 2 х – 3) .
L Неправильное решение.
Разделим обе части уравнения на квадратный трехчлен, записанный в скобках, и получим:
J Правильное решение.
Перенесем правую часть исходного уравнения влево и вынесем общий множитель за скобки:
K Упражнение 2. Решить уравнение lg 2 x – lg x = 0 .
L Неправильное решение.
Разделим обе части уравнения на lg x и получим:
J Правильное решение.
Необходимо помнить, что обычно легче исключить посторонний корень, чем найти потерянный.
Посторонние корни
При решении уравнений существуют два диаметрально противоположных мнения относительно полученного результата. Одни считают, что проверка должна производиться всегда, другие считают ее необязательной. На самом деле проверка полученных корней в одних случаях является обязательной и является частью решения уравнения, а в других случаях в проверке необходимости нет.
Проверка полученного решения уравнения обычно делается с целью исключения посторонних корней, которые чаще всего появляются в результате нетождественных преобразований, приводящих к расширению области допустимых значений переменного. Рассмотрим далее некоторые случаи появления посторонних корней.
Это может случиться при умножении обеих частей дробного уравнения на выражение, содержащее неизвестную величину .
K Упражнение. Решить уравнение
| 5 – x | – | 5 + 3х | = 0 . |
| x – 1 | x 2 – 1 |
L Неправильное решение.
Умножим все члены уравнения на х 2 – 1 и получим:
Комментарий . Был приобретен посторонний корень х = 1, в чем можно убедиться с помощью проверки .
J Правильный ответ: х = 0.
Появление посторонних корней может быть вызвано сокращением дроби на множитель, содержащий неизвестную величину .
K Упражнение. Решить уравнение
| х 2 – 81 |
| 2 | + х 2 – | 2 | – 4х = 0 . |
| 3х 2 | 3х 2 |
L Неправильное решение.
После приведения подобных слагаемых получим:
Комментарий . Был приобретен посторонний корень х = 0 .
J Правильный ответ: 4 .
Заметим, что аналогичная ситуация может сложиться и для слагаемых, содержащих переменную под знаком корня или под знаком логарифма.
Очень часто посторонние корни появляются при возведении в четную степень обеих частей уравнения . Рассмотрим следующее иррациональное уравнение и на его примере – процесс появления посторонних корней.
K Упражнение. Решить уравнение √ х + 3 + √ 7 – х = 2 .
L Неправильное решение.
И число –2 , и число 6 содержатся в области допустимых значений переменной х , значит, являются решениями исходного уравнения.
Комментарий . Оба корня посторонние и были приобретены в процессе решения. Как же это произошло? Дело вот в чем. В процессе решения с помощью возведения в квадрат и элементарных преобразований мы перешли от уравнения
Последнему уравнению число –2 удовлетворяет, после подстановки получаем верное равенство 1 = 1 . Предыдущее же уравнение при подстановке –2 дает ложное равенство 1 = –1 , которое стало верным именно в результате возведения в квадрат, ведь 1 2 = (–1) 2 . Число –2 является корнем второго уравнения, для первого – посторонний корень. А вот число 6 не является корнем ни одного из них.
Шестерка выходит на арену при переходе от уравнения
которое уже имеет один корень –2 , к уравнению
Теперь возведение в квадрат превращает ложное равенство 2 = –2 в истинное равенство 4 = 4 , которые соответствуют этим уравнениям для случая х = 6 . Для последнего уравнения 6 – истинный корень, а для предпоследнего – ложный. И вот, путем преобразований мы получаем уравнение
для которого числа –2 и 6 — самые настоящие корни, а для исходного — посторонние. Два раза мы применяли возведение в квадрат и каждый раз приобретали посторонний корень, каждый из которых благополучно преодолел фильтр ОДЗ. В данном случае проверка обязательна.
J Правильный ответ: решений нет.
Необходимо помнить, что если область допустимых значений неизвестного найдена и при решении уравнения получены корни, принадлежащие ей, то проверка корней не нужна, только если при этом в процессе решения все преобразования были тождественными.
Если при решении уравнения используется тот факт, что произведение равно нулю, когда хотя бы один из множителей равен нулю , прежде чем писать ответ, необходимо убедиться, что все найденные корни удовлетворяют условию.
K Упражнение. Решить уравнение ( x – 5) (х + 2) √ х – 3 = 0 .
L Неправильное решение.
Перейдем от данного уравнения у совокупности уравнений:
Комментарий . Число –2 обращает подкоренное выражение х – 3 в отрицательное число, а значит не может быть корнем уравнения.
J Правильный ответ: 5 и 3 .
Часто причиной изменения множества корней уравнения во время его преобразования является применение равенств, правая и левая части которых имеют разные области определения . Таких равенств много, вот некоторые из них:
| x = | x · y |
| y |
| tg ( x + y ) = | tg x + tg y |
| 1 – tg x · tg y |
| sin 2 x = | 2 tg x |
| 1 + tg 2 x |
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области выражения, стоящего в левой части. Поэтому использование этих равенств слева направо может привести к потере корней, а справа налево – к появлению посторонних корней .
L Неправильное решение.
так как х ≥ 3 , то |х – 1| = х – 1 и
Комментарий . Применение формулы √ х · y = √ х · √ y привело к потере корня x = 1 . И вот почему. Исходное уравнение имеет область допустимых значений ∪[3; +∞) , а вот уже ОДЗ уравнения (left| x-1right|cdot sqrt=x-1) – только [3; +∞) , что и привело к потере 1 .
Можем порекомендовать возвести обе части исходного уравнения в квадрат. Это может привести к появлению посторонних корней, избавиться от которых проверкой, как правило, проще, чем заниматься поисками потерянных корней.
J Правильное решение.
(left(x-1 right)^2cdot left(x-3 right)=left(x-1 right)^2;)
(left(x-1 right)^2cdot left(x-3 right)-left(x-1 right)^2=0;)
(left(x-1 right)^2cdot left(x-4 right)=0;)
Проверкой убеждаемся, что оба корня действительные.
Ошибки, связанные с заменой переменной
При решении некоторых уравнений достаточно удачным является метод замены переменной . Но применение этого метода учащиеся осуществляют не всегда правильно.
Так необходимо помнить, что при наличии нескольких степеней заменять новой переменной надо ту, у которой показатель наименьший .
K Упражнение. Решить уравнение (5 left(x-3 right)^-6=left(x-3 right)^.)
L Неправильное решение.
Сделав замену ( left(x-3 right)^=t), считают, что ( left(x-3 right)^=t^2) и уравнение переписывают в виде 5t 2 – t – 6 = 0 , после чего, конечно, верный результат уже не получить.
J Правильное решение.
Верный результат можно получить, сделав замену ( left(x-3 right)^=t), тогда ( left(x-3 right)^=t^2) с продолжением:
Правильно сделав замену и верно найдя значение вспомогательной переменной, учащиеся часто допускают ошибку, используя не то равенство, которым вспомогательная переменная вводилась .
K Упражнение. Решить уравнение х + 4 √ x – 5 = 0 .
L Неправильное решение.
Комментарий . После нахождения значений вспомогательной переменной t для нахождения х следовало использовать подстановку √ x = t , а не x = t 2 .
J Правильное решение.
При решении иррациональных уравнений учащиеся чаще всего применяют метод возведения в соответствующую степень. В результате этого решения иррациональных уравнений получаются громоздкими и не всегда доводятся до конца .
K Упражнение. Решить уравнение (x^2-4x-sqrt=6.)
L Неправильное (нерациональное) решение.
Чаще всего данное уравнение начинают решать так:
Нередко продолжения решения не следует, так как с полученным уравнением четвертой степени справится не каждый.
Комментарий . В качестве альтернативы можно предложить способ введения новой переменной.
J Правильное решение.
и исходное уравнение принимает вид:
А дальше все просто:
Комментарий . Числа –2 и 6 не подвергались проверке осознанно. В данном случае после возведения в квадрат не могли появиться посторонние корни, так как и квадратный корень, и подкоренное выражение после возведения в квадрат заведомо равны положительным числам.
Ошибки, связанные с использованием модуля
При решении уравнений, в тех случаях, когда необходимо использовать понятия модуля и арифметического корня , допускаются серьезные ошибки, связанные либо с незнанием, либо с непониманием этих понятий.
K Упражнение 1. Решить уравнение (sqrt=9.)
L Неправильное решение.
J Правильное решение.
K Упражнение 2. Решить уравнение (sqrt=x+3.)
L Неправильное решение.
Ответ: корнем данного уравнения является любое действительное число.
J Правильное решение.
Учитывая, что решение уравнений, содержащих модуль, часто вызывает затруднения, приведем полное и развернутое решение одного из таких уравнений.
K Упражнение. Решить уравнение |x – 3| + |x –4| = 1 .
J Правильное решение.
Находим нули модулей, для |х – 3| это 3 , для |x – 4| это 4 , и разбиваем ими область допустимых значений неизвестного на числовые промежутки:
На каждом из этих промежутков исходное уравнение принимает свой вид.
1) при х ∈ (–∞; 3) исходное уравнение принимает вид:
так как 3 ∉ (–∞; 3 ) , то на этом промежутке решений нет;
2) при х ∈ [3; 4) исходное уравнение принимает вид:
что является истинным тождеством; значит, каждое число рассматриваемого промежутка [3; 4) является решением уравнения;
3) при х ∈ [4; +∞) исходное уравнение принимает вид:
так как 4 ∈ [4; +∞) , то 4 – корень уравнения.
Так как [3; 4)∪ = [3; 4] , то корнями исходного уравнения являются все числа числового промежутка [3; 4] .
Подбор корней без обоснования
К ошибочным решениям можно отнести и верный подбор корня заданного уравнения, иногда просто угадывание, без доказательства его единственности .
K Упражнение. Решить уравнение х (х + 1) (х + 2) (х + 3) = 24 .
L Неправильное решение.
Подбором находят корень х = 1 из разложения 24 = 1 · 2 · 3 · 4.
Комментарий . Был подобран корень х = 1 , но не обнаружен еще один корень х = –4 , который соответствует разложению 24 = –4 · (–3) · (–2) · (–1) . Но даже если и второй корень успешно подобран, но не обосновано отсутствие других корней, то считать такое решение уравнения правильным нельзя.
J Правильное решение.
введем новую переменную x 2 + 3х + 1 = t , тогда
1) x 2 + 3х + 1 = –5, x 2 + 3х + 6 = 0, решений нет;
Наиболее распространенным методом доказательства единственности корня нестандартного уравнения является использование свойства монотонности входящих в уравнение функций . Часто при этом используется производная.
K Упражнение. Решить уравнение x 11 + 5х – 6 = 0 .
L Неправильное решение.
Методом подбора находим корень уравнения х = 1 .
Комментарий . Не приведено обоснование единственности подобранного корня уравнения.
J Правильное решение.
Корень х = 1 легко угадывается, а производная левой части равна 11x 10 + 5 и положительна на всей числовой оси. Отсюда следует монотонность функции у = x 11 + 5х – 6 , что и доказывает единственность подобранного корня.
Ошибки в логарифмических и показательных уравнениях
Для решения логарифмических и показательных уравнений используются специальные приемы, основанные на свойствах логарифмов и степеней. Рассмотрим связанные с применением этих приемов ошибки.
При решении уравнений, которые можно свести к равенству степеней с одинаковыми основаниями или с одинаковыми показателями , не всегда делаются правильные выводы.
K Упражнение 1. Решить уравнение (log7 x) 1 /3 = 1 .
L Неправильное решение.
Так как при одинаковых основаниях показатели не равны, то равенство степеней невозможно, а, значит, корней нет.
Ответ: корней нет.
J Правильное решение.
Возведем в куб обе части уравнения, тогда
K Упражнение 2. Решить уравнение (х + 5) х 2 + х – 2 = 1 .
L Неправильное решение.
Комментарий . Потерян корень х = –4 . Избежать этого можно было и при данном способе решения уравнения, если учесть, что степень равна 1 не только в случае нулевого показателя, но и в случае основания равного 1 при произвольном показателе. И тогда в дополнение к приведенному решению имеем:
J Правильное решение.
Прологарифмируем обе части уравнения по некоторому основанию, например 10, при условии х > 5 , тогда
Необходимо помнить, что:
из равенства степеней, основания которых равны единице, не следует обязательное равенство показателей этих степеней;
степенно–показательное уравнение предпочтительно решать путем логарифмирования.
При решении логарифмических уравнений часто приходится применять свойства логарифмов с одинаковыми основаниями . При применении этих свойств учащиеся часто допускают ошибки.
L Неправильное решение.
Комментарий . В решении допущены две серьезные ошибки: во-первых, произведение логарифмов двух чисел заменено логарифмом произведения этих чисел; во-вторых, при решении уравнения 3х 2 = 81x потерян корень х = 0 (этот корень, конечно, не является корнем исходного уравнения, что не оправдывает его потерю).
J Правильное решение.
K Упражнение 2. Решить уравнение lg x 2 = 4 .
L Неправильное решение.
J Правильное решение 1.
2lg |x| = 4; lg | x| = 2; |x| = 100; x = ±100.
J Правильное решение 2.
lg x 2 = lg 10000; x 2 = 10000; x = ±100.
Большие затруднения у многих учащихся возникают при выполнении действий над логарифмами с разными основаниями , так как учащиеся либо не умеют пользоваться соответствующими формулами, либо не знают их.
Следует помнить, что переход к логарифму с другим основанием может привести как к приобретению посторонних корней, так и к потере корней .
K Упражнение 1. Решить уравнение (left(log_5 +2 right)<log _>^2 ;x=0.)
L Неправильное решение.
(left(1 +2 log _xright)log _x=0;)
Комментарий . Преобразование логарифма с основание х в логарифм с основанием 5 привело к появлению постороннего корня, так как произошло расширение ОДЗ.
J Правильное решение.
Приведенное выше решение следует дополнить указанием области допустимых значений неизвестного в исходном уравнении. Это объединение числовых промежутков (0; 1)∪(1; +∞) . И указанием того факта, что 1 ∉ (0; 1)∪(1; +∞) , а, значит, не является корнем.
K Упражнение 2. Решить уравнение (20log_sqrt+ 7log_x^3-3log _x^2=0.)
L Неправильное решение.
Комментарий . В приведенном решении потерян корень, и вот почему. Был выполнен переход к логарифму с основанием х . Это вызвало изменения в ОДЗ неизвестного. Одно из таких изменений – это х ≠ 1 . Поэтому число 1 , как возможный корень исходного уравнения, следует рассмотреть отдельно.
J Правильное решение.
Приведенное выше решение нужно дополнить лишь проверкой того, не является ли 1 корнем уравнения. Подставляем 1 в исходное уравнение и убеждаемся, что 1 – корень.
Ошибки в тригонометрических уравнениях
Выделение в отдельный подраздел тригонометрических уравнений связано стем, что при их решении применяются не только алгебраические методы. Рассмотрим наиболее типичные ошибки, которые допускают учащиеся при решении тригонометрических уравнений.
Часто можно встретить неправильную запись решения тригонометрического уравнения или лишь частное решение .
Видео:Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

Учитель допустил ошибку на доске, а когда дети начали смеяться над ним, объяснил им простую истину…
Однажды школьный учитель написал на доске следующее:
Когда она закончила, она посмотрела на учеников, и все они смеялись над ней из-за первого уравнения, которое было не правильное, а затем учитель сказала следующее:
«Я написала первое уравнение неправильно, потому что я хотела, чтобы вы научились чему-то очень важному. Это урок для вас, который показывает, как мир будет относиться к вам. Вы видите, что я написала 9 уравнений правильно, но никто из вас меня не поздравил, но вы все рассмеялись и критиковали меня из-за одного неправильного уравнения, которое я написала.
Мир никогда не оценит добрые дела, которые вы будете делать миллион раз, но будет критиковать неправильный поступок, который вы сделаете все один раз…
🔍 Видео
Простые уравнения. Как решать простые уравнения?Скачать

Линейные и квадратные уравнения №9 из ОГЭ.Скачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

РОЛИК по №8. Грамматические ошибки. Вся теория.Скачать

Решаем вместе 8 задание ЕГЭ (поиск грамматических ошибок)Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Как решают уравнения в России и СШАСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Сложные уравнения. Как решить сложное уравнение?Скачать

16. Решение уравненийСкачать

Это уравнение сломает твоего учителя!Скачать

Решение систем уравнений методом подстановкиСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Уравнение с четырьмя неизвестнымиСкачать

Решение всех прототипов №20 из ОГЭ по математике. Уравнения, неравенства, системы.Скачать

Путин про ядерный ответ #shortsСкачать