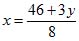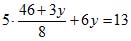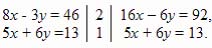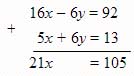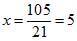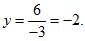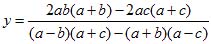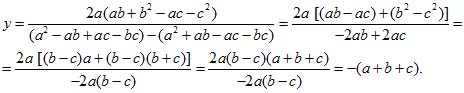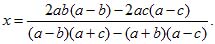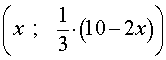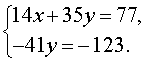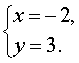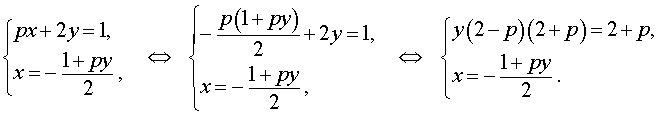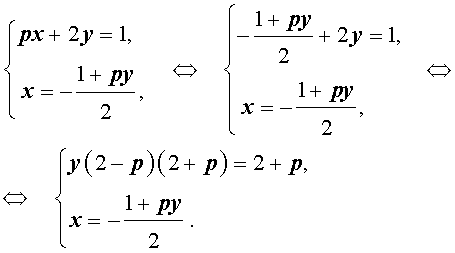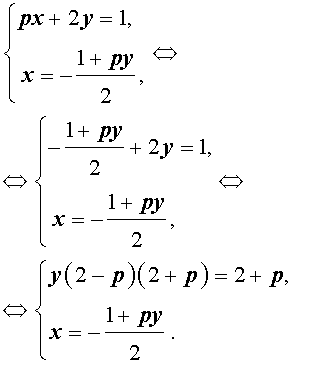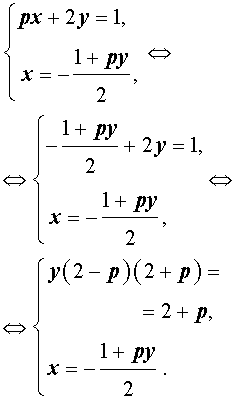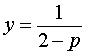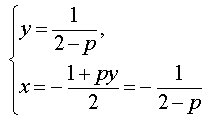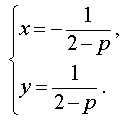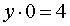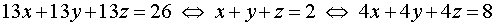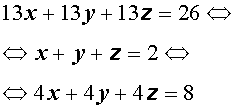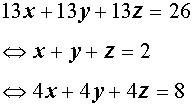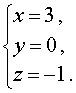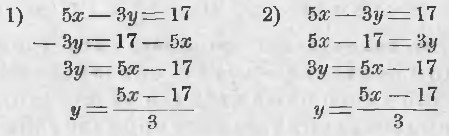а) Способ подстановки состоит в том, что:
1) из одного уравнения мы находим выражение одного из неизвестных, например x, через известные величины и другое неизвестное у,
2) найденное выражение подставляем во второе уравнение, в котором после этой подстановки будет содержаться только одно неизвестное у;
3) решаем полученное уравнение и находим значение у; 4) подставляя найденное значение у в выражение неизвестного x, найденное в начале решения, получаем значение х.
Пример. Решить систему уравнений:
8x – 3y = 46, 5x + 6y = 13.
1) Из первого уравнения находим выражение х через данные числа и неизвестное у:
2) Подставляем это выражение во второе уравнение:
3) Решаем полученное уравнение:
5(46+3y)/8 + 48y/8 = 13, 5(46+3y) + 48y = 104, 230 + 15y + 48y = 104, 15y+48y = 104 – 230, 63y = — 126, y = — 2.
4) Найденное значение y = — 2 подставляем в выражение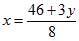 
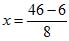
; получаем 
, т.е. x = 5.
Способ сложения или вычитания
1) обе части одного уравнения умножаются на некоторый множитель; обе части второго уравнения умножаются на другой множитель. Эти множители подбираются так, чтобы коэффициенты при одном из неизвестных в обоих уравнениях после их умножения на эти множители имели одну, и ту же абсолютную величину.
2) Складываем два уравнения или вычитаем их друг из друга, смотря по тому, имеют ли уравненные коэффициенты различные или одинаковые знаки; этим одно из неизвестных исключается.
3) Решаем полученное уравнение с одним неизвестным.
4) Другое неизвестное можно найти тем же приемом, но обычно, проще всего подставить найденное значение первого неизвестного в любое из данных уравнений и решить получившееся уравнение с одним неизвестным.
Пример. Решить систему уравнений:
8x – 3y = 46, 5x + 6y = 13.
1) Проще всего уравнять абсолютные величины коэффициентов при у; обе части первого уравнения умножим на 2; обе части второго — на 1, т. е. оставляем второе уравнение неизменным:
2) Складываем два уравнения:
3) Решаем полученное уравнение:
4) Подставляем значение x = 5 в первое уравнение; имеем: 40 — 3y = 46; — 3y = 46 – 40; — 3y = 6. Отсюда
Способ сложения и вычитания следует предпочесть другим способам:
1) когда в данных уравнениях абсолютные величины коэффициентов при одном из неизвестных равны (тогда первый из этапов решения становится ненужным);
2) когда сразу видно, что числовые коэффициенты при одном из неизвестных уравниваются с помощью небольших целочисленных множителей;
3) когда коэффициенты уравнений содержат буквенные выражения.
Пример. Решить систему:
(a + c)x – (a – с)y = 2ab, (a + b)x – (a — b)y = 2ac.
1) Уравниваем коэффициенты при х, помножая обе части первого уравнения на (a + b), а второго на (а + с), получаем:
(a + c)(a +b)x – (a + b)(a — c)y = 2ab(a + b), (a +c)(a +b)x – (a-b)(a + c)y = 2ac(a +c).
2) Вычитаем из первого уравнения второе; получаем:
[(a — b)(a + c) – (a + b)(a — c)]y = 2ab(a + b) – 2ac(a + c).
3) Решаем полученное уравнение:
Это выражение можно значительно упростить, для чего однако, потребуются довольно долгие преобразования. В числителе и знаменателе раскроем скобки,
4) Чтобы найти x, уравняем коэффициенты при y в исходных уравнениях, помножив первое на (a — b), второе на (a — с). Вычтя одно полученное уравнение из другого, решим уравнение с одним неизвестным; найдем:
Выполняя такие же преобразования, как в предыдущем пункте, получим х = b + c — a. Подстановка значения y d одно из исходных уравнений потребовала бы более утомительных вычислений; при решении буквенных уравнений так бывает очень часто.
Видео:Решение систем уравнений методом подстановкиСкачать
Системы линейных уравнений
 Линейные уравнения (уравнения первой степени) с двумя неизвестными |
| Системы из двух линейных уравнений с двумя неизвестными |
| Системы из трех линейных уравнений с тремя неизвестными |
Видео:Алгебра 7 класс (Урок№46 - Системы двух уравнений первой степени с двумя неизвестными.)Скачать
Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
| ax +by = c , | (1) |
где a , b , c – заданные числа.
Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1 . Найти решение уравнения
| 2x +3y = 10 | (2) |
Решение . Выразим из равенства (2) переменную y через переменную x :
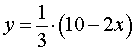 | (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Видео:Алгебра 7 класс (Урок№45 - Уравнения первой степени с двумя неизвестными.)Скачать
Системы из двух линейных уравнений с двумя неизвестными
Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
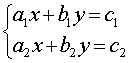 | (4) |
Определение 4 . В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных , а числа c1 , c2 – свободными членами .
Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «
»
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
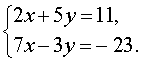 | (5) |
Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
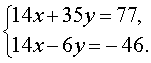 | (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Пример 3 . Найти все значения параметра p , при которых система уравнений
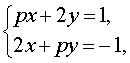 | (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
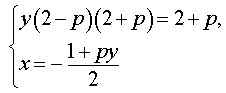 | (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если 
, то уравнение (9) имеет единственное решение
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда , система (7) имеет единственное решение
Если p = – 2 , то уравнение (9) принимает вид
,
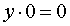
и его решением является любое число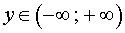 
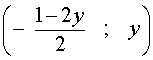
. Поэтому решением системы (7) служит бесконечное множество всех пар чисел
,
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Видео:Решение систем уравнений второго порядка. 8 класс.Скачать
Системы из трех линейных уравнений с тремя неизвестными
Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
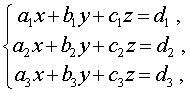 | (10) |
Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
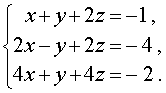 | (11) |
Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
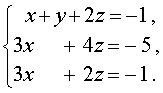 | (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
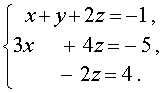 | (13) |
Из системы (13) последовательно находим
Пример 5 . Решить систему уравнений
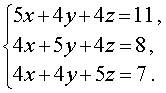 | (14) |
Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать
Математика
55. Уравнение с двумя неизвестными. Рассмотрим теперь уравнение
Оно является записью задачи: найти числовые значения для x и y, чтобы двучлен 5x + 3y оказался равным числу 18.
Мы знаем, что если бы в этом двучлене было бы лишь одно неизвестное число, то и тогда мы сумели бы решить соответствующее уравнение. Поэтому возникает соображение, что здесь одно из неизвестных является как бы лишним: если взамен неизвестного y, например, взять какое угодно число, то мы получим уравнение с одним неизвестным.
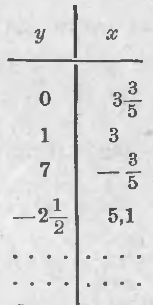
А если так, то данное уравнение должно иметь сколько угодно решений, и выясняется способ их получения: станем давать одному из неизвестных, например, y, произвольные значения и всякий раз из получаемого уравнения с 1 неизвестным станем определять другое неизвестное x. Чтобы придать этой работе больше порядка, будем результаты ее записывать в таблице.
Дадим y значение 0, т. е. примем, что y = 0 (записано в первой строчке таблицы). Тогда наше уравнение обратится в
(в таблице записываем это число во втором столбце, озаглавленном буквою x).
Итак, мы получили одно решение нашего уравнения: y = 0 и x = 3(3/5) (если эти значения подставить в наш двучлен вместо x и y, то требование, чтобы двучлен равнялся числу 18, оправдается:
3 * 3(3/5) + 3 * 0 = 18).
Дадим y значение 1, т. е. примем, что y = 1 (вторая строчка таблицы); тогда получим
откуда 5x = 18 – 3 или 5x = 15 и x = 3 (записано во 2-ой строчке). Итак, найдено второе решение уравнения y = 1 и x = 3.
Дадим y значение 7, т. е. примем, что y = 7; тогда получим уравнение 5x + 21 = 18, откуда 5x = –3 и x = –3/5 (см. 3-ю строчку таблицы).
Примем еще y = –2½; тогда 5x + 3(–2½) = 18 или 5x – 7½ = 18, откуда 5x = 25½ и x = 5(1/10) = 5,1 (см. 4-ю строчку таблицы). Эту работу можно продолжить сколь угодно далеко. Итак, одно уравнение с двумя неизвестными имеет бесконечно много решений; для их получения надо одному неизвестному давать произвольные значения и из получаемых уравнений определять всякий раз другое неизвестное .
Рассматривая предыдущую таблицу и вспоминая п. 49, мы установим: у нас y был независимым переменным, x — зависимым, или x является функцией y – a.
Мы можем несколько ускорить работу нахождения решений данного уравнения. Сочтем y за известное число (все равно, ведь, y мы всякий раз заменяли известным числом); тогда на уравнение 5x + 3y = 18 мы можем смотреть, как на уравнение с одним неизвестным x и решим это уравнение:
5x = 18 – 3y; x = (18 – 3y) / 5
Мы можем этот результат выразить словами так: мы из данного уравнения определили y через x .
Теперь по формуле (18 – 3y) / 5 мы можем легко найти сколько угодно решений, делая вычисления в уме. Примем, например, y = 2. Тогда надо (–3) умножить на (+2), получим –6; сложить (+18) и (–6) — получим +12 и разделить на 5 — получим x = +2(2/5). Еще пусть y = 10; тогда (–3) · (+10) = –30; (+18) + (–30) = –12; (–12) : (+5) = –2(2/5), т. е. x = –2(2/5) и т. д.
Возьмем еще уравнение:
Примем за независимое переменное x, а за зависимое y и определим y через x. Это можно сделать двумя приемами:
Быть может второй прием удобнее 1-го, так как его выполнение легче поддается воображению, если желательно выполнить определение y-а через x в уме.
Теперь мы можем найти сколько угодно решений нашего уравнения: 1) x = 0; y = –5(2/3); 2) x = 1; y = –4; 3) x = –1; y = –7(1/3) и т. д.
Следует приучиться быстро (в уме) определять одно из неизвестных данного уравнения с двумя неизвестными через другое. Примеры:
f55_3
📹 Видео
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Системы двух уравнений первой степени с двумя неизвестнымиСкачать
Уравнения первой степени с двумя неизвестными. Системы уравнений.Скачать
7 класс. Уравнения первой степени с двумя неизвестными.Скачать
Линейное уравнение с двумя переменными. 7 класс.Скачать
Уравнения первой степени с двумя неизвестнымиСкачать
Системы двух уравнений первой степени с двумя неизвестнымиСкачать
Понятие системы уравнений - ЧАСТЬ 1Скачать
Графический способ решения систем двух уравнений первой степени с двумя неизвестнымиСкачать
Решение системы линейных уравнений графическим методом. 7 класс.Скачать
Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать
Решение систем уравнений. Методом подстановки. Выразить YСкачать
Графический способ исследования систем двух уравнений первой степени с двумя неизвестнымиСкачать
Решение систем уравнений второй степени. Алгебра, 9 классСкачать
Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать
