Читайте также:
|
| Предмет: | Физика |
| Тип работы: | Курсовая работа |
| Язык: | Русский |
| Дата добавления: | 21.05.2019 |
- Данный тип работы не является научным трудом, не является готовой выпускной квалификационной работой!
- Данный тип работы представляет собой готовый результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала для самостоятельной подготовки учебной работы.
Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!
По этой ссылке вы сможете найти много готовых курсовых работ по физике:
Посмотрите похожие темы возможно они вам могут быть полезны:
Введение:
Беспорядок теплового движения молекул газа, постоянные столкновения между ними приводят к постоянному перемешиванию частиц и изменению их скоростей и энергий. Если в газе существует пространственная неоднородность плотности, температуры или скорости упорядоченного движения отдельных слоев газа, то движение молекул выравнивает эти неоднородности. В этом случае в газе возникают особые процессы, объединенные общим названием транспортных явлений. Эти явления включают диффузию, внутреннее трение и теплопроводность. Общим для всех транспортных явлений является то, что они возникают в газах в результате нарушения полного хаоса молекулярного движения. Эти нарушения вызваны направленным воздействием на газ: в случае диффузии должна быть создана неоднородность плотности, в случае теплопроводности — неоднородность температуры, в случае внутреннего трения — упорядочение движения газа. молекулы со скоростями, которые не одинаковы в разных его слоях.
Изучение явлений переноса представляет особый интерес в связи с тем, что эти явления позволяют экспериментально определить такие важные характеристики молекул, как длина пробега и эффективный диаметр.
Транспортные явления в газах. Общие закономерности
Феномен переноса — диффузии — состоит в самопроизвольном взаимном проникновении и смешивании частиц двух контактирующих газов, жидкостей и даже твердых тел. В то же время различается самодиффузия — проникновение атомов и молекул одного и того же вида между молекулами одного типа и гетеродиффузия — проникновение молекул или атомов одного вида между атомами или молекулами другого рода. В химически чистых газах диффузия происходит из-за неодинаковой плотности в разных частях объема газа. В случае газовой смеси причиной диффузии является разница в концентрации отдельных газов в разных частях объема смеси. Если это явление не осложняется изменением температуры по объему газа, то оно заключается в переносе массы газа из мест с более высокой концентрацией данного газа в места с более низкой концентрацией.
Экспериментально установлено, что перенос массы вещества при явлении диффузии подчиняется закону А. Фика.
Масса газа, которая передается в единицу времени через элемент поверхности, взятый внутри газа, площадь которого равна единице, прямо пропорциональна скорости изменения плотности газа r на единицу длины x в направлении нормаль к рассматриваемой области.
Если элемент поверхности выбран так, что нормаль совпадает с направлением самого быстрого уменьшения плотности r, то он численно равен градиенту плотности. Значение D называется коэффициентом диффузии. Коэффициент диффузии — это физическая величина, численно равная массе вещества, переносимого через единицу поверхности за единицу времени с градиентом плотности, равным единице. В системе единиц СИ коэффициент диффузии измеряется в м2 / с, в системе CGS — в см2 / с. Знак минус в формуле (10.5) указывает на то, что массообмен происходит в направлении уменьшения плотности.
Феномен внутреннего трения (вязкости) связан с возникновением сил трения между слоями газа или жидкости, движущимися параллельно друг другу с разными скоростями. Со стороны слоя, движущегося быстрее, на медленный движущийся слой действует ускоряющая сила. И наоборот, медленно движущийся слой замедляет более быстро движущиеся слои газа. Силы трения, возникающие в этом случае, направлены тангенциально к поверхности контакта слоев.
С точки зрения кинетической теории газов причиной внутреннего трения является суперпозиция упорядоченного движения слоев газа с разными скоростями V1 и V2 и хаотического теплового движения молекул, интенсивность которого зависит от температуры. Из-за теплового движения молекулы движутся от слоя B, движущегося со скоростью V2, к слою A, движущемуся со скоростью V1.
В этом случае молекулы из слоя B «переносят» на слой A импульсы mV2 своего упорядоченного движения. Если V1> V2, то такие молекулы при столкновениях с частицами слоя А ускоряют свое упорядоченное движение, а молекулы слоя А замедляются. Напротив, когда молекулы переходят из быстро движущегося слоя A в слой B, они передают большие импульсы mV1, и столкновения между молекулами приводят к ускорению упорядоченного движения молекул слоя B.
Феномен внутреннего трения, как показал опыт, подчиняется закону И. Ньютона: где dF — внутренняя сила трения, действующая на единицу dS площади поверхности слоя, представляет собой изменение скорости слоев на единицу длины X в направлении внутренней нормали к поверхности слоя и представляет собой градиент скорости.
Знак минус в формуле показывает, что сила dF противоположна в направлении производной X от вектора скорости газа V. Значение h называется коэффициентом внутреннего трения, или динамической вязкостью, и измеряется в Единицы СИ в кг / (м × сек) или N × сек / м2, в системе CGS — в г / (см × сек). Коэффициент внутреннего трения численно равен внутренней силе трения, действующей на единицу площади поверхности слоя с градиентом скорости, равным единице.
Теплопроводность
Теплопроводность возникает при разнице температур в газе, вызванной некоторыми внешними причинами. Молекулы газа в разных местах своего объема имеют разные средние кинетические энергии. Поэтому во время хаотического теплового движения молекул происходит направленная передача энергии. Явление теплопроводности возникает, если разные слои газа имеют разные температуры, то есть имеют разную внутреннюю энергию. Молекулы, попавшие из нагретых частей газа в более холодные, отдают свою избыточную энергию окружающим частицам. Наоборот, медленно движущиеся молекулы, падая от холодных частей к более горячим, увеличивают свою энергию из-за столкновений с молекулами с высокими скоростями.
Процесс передачи внутренней энергии в форме тепла происходит таким образом, что количество тепла dQ, передаваемого в единицу времени через единицу площади, прямо пропорционально скорости изменения температуры на единицу длины X в направлении нормали п в этой области.
Формула была установлена Дж. Фурье и называется законом теплопроводности Фурье. Здесь K — коэффициент теплопроводности, а знак минус показывает, что энергия передается в направлении снижения температуры.
Коэффициент теплопроводности показывает, сколько тепла передается через единицу площади за единицу времени с градиентом температуры, равным единице.
В системе единиц СИ теплопроводность измеряется в Дж / (м × с × К), а в системе CGS — в эрг / (см × с × град).
Вывод значений коэффициентов D, h и K, их связь друг с другом и зависимость от параметров газа.
Мы не ставим перед собой задачу представить строгие методы расчета явлений переноса в газах. Впервые такой расчет был проведен Д. К. Максвеллом на основе детального изучения динамики молекулярных столкновений. Мы рассмотрим только основные законы транспортных явлений и их приближенное качественное обоснование.
Закономерности всех явлений переноса схожи. Выражения являются макроскопическими и не раскрывают молекулярно-кинетический смысл коэффициентов переноса D, h, K. их энергии и т. д.). Мы рассмотрим эту связь более подробно на примере явления диффузии, а для двух других явлений мы представим только результаты. В этом случае мы ограничимся качественным аспектом вопроса, поскольку, как уже указывалось, строгий учет явлений переноса связан со значительными трудностями.
Предположим, что плотность химически однородного газа зависит от координат и различна в разных частях объема газа. Смешивание молекул в результате их теплового движения приводит к переносу массы газа в направлении уменьшения плотности, то есть к выравниванию плотности газа по всему объему. Чтобы существовал непрерывный, не зависящий от времени (стационарный) перенос массы газа, необходимо внешнее воздействие. Он должен поддерживать постоянное распределение плотности по объему газа и нейтрализовать выравнивание плотности из-за диффузионного процесса.
Коэффициент самодиффузии D:
- n1> n2, r1> r2, T1 = T2, массы всех молекул одинаковы
- r1 r2 X и равны m.
- n1 n2.
Мы ограничимся простейшим случаем, когда плотность r зависит только от одной координаты X [r = r (X)], иными словами, плотность газа одинакова во всех точках плоскости, перпендикулярной оси X. Из молекул, содержащихся в единице объема газа, одна треть движется вдоль оси X, одна треть вдоль оси Y и одна треть вдоль оси Z. Движение молекул вдоль каждой оси в обоих направлениях одинаково вероятно. Следовательно, одна шестая часть общего количества молекул движется в положительном направлении оси X. В дальнейшем мы будем предполагать, что все молекулы имеют одинаковую скорость теплового движения, равную их средней скорости (T = const). Если бы плотность газа r была постоянной по всему объему, то через единицу площади плоской поверхности S, перпендикулярной оси X (фиг.10.4), такое же количество молекул прошло бы слева направо и из справа налево за единицу времени (нет — количество молекул на единицу объема). Однако в рассматриваемом случае r = r (x). Поскольку n1> n2, разное количество молекул переносится слева направо и справа налево за единицу времени по поверхности S, то есть направленный перенос частиц и, следовательно, их массы происходит в газе.
При нахождении числа «n» молекул, проходящих в единицу времени через область S вдоль положительного направления оси X, необходимо принять значения n1, в отличие от n2 для молекул, движущихся в противоположном направлении. На пути свободного пробега ни величина, ни направление скоростей молекул не меняются. Поэтому в среднем можно предположить, что одна шестая часть всех молекул, отстоящих от нее с обеих сторон на расстоянии средней длины свободного пробега , может свободно достигать поверхности S.
Вывод:
Некоторые важные выводы вытекают из формул для коэффициентов переноса. Оказывается, что коэффициенты внутреннего трения и теплопроводности не зависят от давления газа. Этот факт, впервые обнаруженный Д. К. Максвеллом, на первый взгляд кажется парадоксальным, хотя и согласуется с экспериментальными данными в случае не слишком разреженных газов. Это объясняется тем, что с ростом давления большее количество молекул участвует в передаче импульса и внутренней энергии, но каждая из них проходит короткие расстояния без столкновения, так что в целом передача импульса и энергии не изменение. Таким образом, снижение давления воздуха в 500 раз приводит к изменению динамической вязкости всего на 4%. Формально это сводится к тому, что в формулах (10.10) и (10.11) для коэффициентов внутреннего трения и теплопроводности плотность (и, следовательно, давление) падает, поскольку обратно пропорциональна плотности р. Существуют простые зависимости между коэффициентами переноса, вытекающие из формул (10.9) — (10.11):
Эти формулы показывают, что значения коэффициента внутреннего трения, теплопроводности или диффузии, найденные из опыта, могут быть использованы для определения оставшихся коэффициентов передачи.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
📺 Видео
Явления переноса Теплопроводность и вязкостьСкачать

Закон диффузии ФикаСкачать

Явление переноса в газах, Киевнаучфильм, 1980Скачать

27. Уравнения переносаСкачать

Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Явления переноса в газах. Вязкость газаСкачать

Олимпиадная физика в деталях: явления переноса | Третий выпускСкачать

Лекция по физике для втузов. 13-14. Явления переноса: теплопроводность, вязкость, диффузияСкачать

Вязкость газов.Скачать

Физическая кинетика. Часть 2. Явление переноса. Диффузия.Скачать

Вязкость и течение Пуазёйля (видео 14) | Жидкости | ФизикаСкачать

Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать

Видеолекция "Явления переноса. Реальные газы"Скачать

Физический кружок: физическая кинетика | Восьмое занятиеСкачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Урок 12 (осн). Диффузия. Броуновское движениеСкачать

Галилео. Эксперимент. Вязкость воздухаСкачать

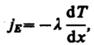 (48.1)
(48.1) 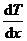 — градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки jE и
— градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки jE и 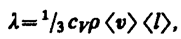 (48.2)
(48.2) 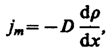 (48.3)
(48.3) 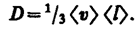 (48.4)
(48.4) 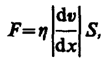 (48.5)
(48.5) 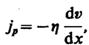 (48.6)
(48.6)  — градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки jр и
— градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки jр и 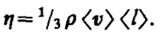 (48.7)
(48.7)