| Название | Линейная балансовая модель. |
| Анкор | История Росии |
| Дата | 23.06.2021 |
| Размер | 77 Kb. |
| Формат файла |  |
| Имя файла | Реферат.doc |
| Тип | Реферат #220799 |
 С этим файлом связано 66 файл(ов). Среди них: Практическая работа (38).doc, История России.docx, Кейс.docx ПСИХОЛОГИЯ (3) (1).docx, Психология_здоровья_Структура_здоровья.docx, rabota_1.docx, Качество информации как движущий фактор развития экономики.docx, Письменная работа — 2022-01-05T174904.121.docx, Письменная работа — 2022-01-05T173027.640.docx о Лазиза.docx, Письменная работа (35).doc, Экономика организации (1).docx, Реферат (23).docx, Контрольная Работа (11).docx, Негосударственное образовательное учреждение (2).docx, Экономика организации (2).docx, Экономическая теория (кейс).docx, Частное учреждение образовательная организация высшего образован, Институциональная экономика.docx ББ (1).docx, Частное учреждение образовательная организация высшего образован, Контрольная работа (1).docx, Письменная работа — 2021-12-25T214735.826 (1).docx, контрпольная работа.docx, Письменная работа — 2021-12-22T231150.301 (3).docx, Практическая работа (36) (1).doc, Письменная работа — 2021-12-25T215016.415.docx, МУ Б1.О.02.02 Иностранный язык.docx, Псих.2 (2).docx, реферат (31).doc, Бинарный поиск.doc, Реферат (19).doc, Кейс.docx, Кейс.docx ПСИХОЛОГИЯ.docx, Английский часть 3 практика (2).doc, ПИСЬМЕННАЯ РАБОТА (29).doc, Практическая работа (28).doc, Практическая работа (26).doc, REFERAT.doc, Иностранных язык .doc, Письменная работа (11).rtf, Письменная работа (3).doc, Реферат (16).docx, Денежная экономика в анализе Ирвинга Фишера.doc, Негосударственное образовательное учреждение.docx, ПРАКТИЧЕСКАЯ РАБОТА Русский язык и культура общения (3).doc, ПРАКТИЧЕСКАЯ РАБОТА Русский язык и культура общения (1).doc, Письменная работа (26).docx, Экономическая теория. реферат.doc, бухгалтерия Баланс (4).docx, ПРАКТИЧЕСКАЯ РАБОТА Русский язык и культура общения (1).doc, Реферат Информационно-коммуникационные технологии в быту.docx и ещё 56 файл(а). С этим файлом связано 66 файл(ов). Среди них: Практическая работа (38).doc, История России.docx, Кейс.docx ПСИХОЛОГИЯ (3) (1).docx, Психология_здоровья_Структура_здоровья.docx, rabota_1.docx, Качество информации как движущий фактор развития экономики.docx, Письменная работа — 2022-01-05T174904.121.docx, Письменная работа — 2022-01-05T173027.640.docx о Лазиза.docx, Письменная работа (35).doc, Экономика организации (1).docx, Реферат (23).docx, Контрольная Работа (11).docx, Негосударственное образовательное учреждение (2).docx, Экономика организации (2).docx, Экономическая теория (кейс).docx, Частное учреждение образовательная организация высшего образован, Институциональная экономика.docx ББ (1).docx, Частное учреждение образовательная организация высшего образован, Контрольная работа (1).docx, Письменная работа — 2021-12-25T214735.826 (1).docx, контрпольная работа.docx, Письменная работа — 2021-12-22T231150.301 (3).docx, Практическая работа (36) (1).doc, Письменная работа — 2021-12-25T215016.415.docx, МУ Б1.О.02.02 Иностранный язык.docx, Псих.2 (2).docx, реферат (31).doc, Бинарный поиск.doc, Реферат (19).doc, Кейс.docx, Кейс.docx ПСИХОЛОГИЯ.docx, Английский часть 3 практика (2).doc, ПИСЬМЕННАЯ РАБОТА (29).doc, Практическая работа (28).doc, Практическая работа (26).doc, REFERAT.doc, Иностранных язык .doc, Письменная работа (11).rtf, Письменная работа (3).doc, Реферат (16).docx, Денежная экономика в анализе Ирвинга Фишера.doc, Негосударственное образовательное учреждение.docx, ПРАКТИЧЕСКАЯ РАБОТА Русский язык и культура общения (3).doc, ПРАКТИЧЕСКАЯ РАБОТА Русский язык и культура общения (1).doc, Письменная работа (26).docx, Экономическая теория. реферат.doc, бухгалтерия Баланс (4).docx, ПРАКТИЧЕСКАЯ РАБОТА Русский язык и культура общения (1).doc, Реферат Информационно-коммуникационные технологии в быту.docx и ещё 56 файл(а).  Показать все связанные файлы Подборка по базе: Строение и состав земной коры реферат.doc, логика реферат.docx, ФИзра реферат.rtf, катаракта реферат офтальмология.docx, Литература реферата маркетинг.docx, Хаустова реферат истоки развития скандинавской ходьбы (1).docx, Мой реферат.docx, Экология реферат.docx, 1-Математика — реферат.docx, Чистяков Роман 1об-ИС Разложение вектора на Орты Реферат.docx Показать все связанные файлы Подборка по базе: Строение и состав земной коры реферат.doc, логика реферат.docx, ФИзра реферат.rtf, катаракта реферат офтальмология.docx, Литература реферата маркетинг.docx, Хаустова реферат истоки развития скандинавской ходьбы (1).docx, Мой реферат.docx, Экология реферат.docx, 1-Математика — реферат.docx, Чистяков Роман 1об-ИС Разложение вектора на Орты Реферат.docxВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ТЕМА: «Линейная балансовая модель.» Юлдашева Лазиза Шокир кизи ГЛАВА 1. Линейная балансовая модель……………………………………5 ГЛАВА 2. Решение балансовых уравнений с помощью обратной матрицы…………………………………………………………………………..12 Изучение балансовых моделей, представляющих собой одно из важнейших направлений и экономико-математических исследований, должно служить объектом изучения отдельной дисциплины. Наша цель – проиллюстрировать на примере балансовых расчетов применение основных понятий линейной алгебры. Балансовая модель производства является одной из наиболее простых математических моделей. Она записывается в виде системы уравнений, каждое из которых выражает требование равенства (баланса) между количеством продукции, производимой отдельным экономическим объектом, и совокупной потребностью в этом продукте. Под экономическим объектом обычно понимают так называемую «чистую прибыль». Например, чтобы правильно отразить взаимосвязи между машиностроением и металлургией, необходимо исключить продукцию металлургической и других отраслей из продукции машиностроения, а в продукции металлургической промышленности не учитывать произведенные на металлургических заводах продукты машиностроения и других отраслей. Таким образом, продукция «чистой отрасли» складывается из продукции специализированных предприятий, очищенной от непрофильных ее видов, и продукции, соответствующей профилю данной отрасли, но произведенной на предприятиях, относящихся к другим отраслям Балансовые модели основываются на понятии межотраслевого баланса, который представляет собой таблицу, характеризующую связи между отраслями (экономическими объектами) экономической системы. Предположим, что экономическая система состоит из n взаимосвязанных отраслей P1, Р2, . Рn. Валовой продукт i-й отрасли обозначим через Xi (X1 – валовой продукт P1 Х2 – валовой продукт Р2, . Хn валовой продукт Рn). Конечный продукт каждой отрасли обозначим буквой Y с индексом, соответствующим ее номеру (Yi — конечный продукт Pi). Отрасли взаимосвязаны, т.е. каждая из них использует продукцию других отраслей в качестве сырья, полуфабрикатов и т. п. Пусть Xij – затраты продукции i-й отрасли на производство продукции Рj. Условно чистую продукцию i-й отрасли обозначим Vi. Если перечисленные показатели представлены в межотраслевом балансе в тоннах, литрах, километрах, штуках и т. д., то говорят о межотраслевом балансе в натуральном, выражений. Мы же договоримся, что под Xi, Уj, Vj и Xij будем понимать выраженную в некоторых фиксированных ценах стоимость соответствующей продукции. Такой баланс называется стоимостным. ЦЕЛЬ: Обосновать и рассмотреть основные аспекты линейной балансовой модели. Задачи:
ГЛАВА 1. Линейная балансовая модель Пусть рассматривается экономическая система, состоящая из n взаимосвязанных отраслей производства. Продукция каждой отрасли частично идет на внешнее потребление (конечный продукт), а частично используется в качестве сырья, полуфабрикатов или других средств производства в других отраслях, в том числе и в данной. Эту часть продукции называют производственным потреблением. Поэтому каждая из рассматриваемых отраслей выступает и как производитель продукции (первый столбец таблицы 1) и как ее потребитель (первая строка таблицы 1). Обозначим через xi валовый выпуск продукции i-й отрасли за планируемый период и через yi — конечный продукт, идущий на внешнее для рассматриваемой системы потребление (средства производства других экономических систем, потребление населения, образование запасов и т.д.). Таким образом, разность xi — yi составляет часть продукции i-й отрасли, предназначенную для внутрипроизводственного потребления. Будем в дальнейшем полагать, что баланс составляется не в натуральном, а в стоимостном разрезе. Обозначим через xik часть продукции i-й отрасли, которая потребляется k-й отраслью, для обеспечения выпуска ее продукции в размере хk. Очевидно, величины, расположенные в строках таблицы 1 связаны следующими балансовыми равенствами: 1 Одна из задач балансовых исследований заключается в том, чтобы на базе данных об исполнение баланса за предшествующий период определить исходные данные на планируемый период. Будем снабжать штрихом (х’ik, y’i и т.д.) данные, относящиеся к истекшему периоду, а теми же буквами, но без штриха — аналогичные данные, связанные с планируемым периодом. Балансовые равенства (1) должны выполняться как в истекшем, так и в планируемом периоде. Будем называть совокупность значений y1, y2,…, yn, характеризующих выпуск конечного продукта, ассортиментным вектором: а совокупность значений x1, x2,…, xn, определяющих валовый выпуск всех отраслей — вектор-планом: Зависимость между двумя этими векторами определяется балансовыми равенствами (1). Однако они не дают возможности определить по заданному, например, вектор у необходимый для его обеспечения вектор-план х, т.к. кроме искомых неизвестных хk, содержат n2 неизвестных xik, которые в свою очередь зависят от xk. Поэтому преобразуем эти равенства. Рассчитаем величины aik из соотношений: Величины aik называются коэффициентами прямых затрат или технологическими коэффициентами. Они определяют затраты продукций i-й отрасли, используемые k-й отраслью на изготовление ее продукции, и зависят главным образом от технологии производства в этой k-й отрасли. С некоторым приближением можно полагать, что коэффициенты aik постоянны в некотором промежутке времени, охватывающим как истекший, так и планируемый период, т.е., что 2 Исходя из этого предложения имеем т.е. затраты i-й отрасли в k-ю отрасль пропорциональны ее валовому выпуску, или, другими словами, зависят линейно от валового выпуска xk. Поэтому равенство (5) называют условием линейности прямых затрат. Рассчитав коэффициенты прямых затрат aik по формуле (4), используя данные об исполнении баланса за предшествующий период либо определив их другим образом, получим матрицу, которую называют матрицей затрат. Заметим, что все элементы aik этой матрицы неотрицательны. Это записывают сокращено в виде матричного неравенства А0 и называют такую матрицу неотрицательной. Заданием матрицы А определяются все внутренние взаимосвязи между производством и потреблением. Подставляя значения xik = aik = xk во все уравнения системы (1), получим линейную балансовую модель. Система уравнений (6) может быть записана компактнее, если использовать матричную форму записи уравнений: Уравнения (6) содержат 2n переменных (xi и yi). Поэтому, задавшись значениями n переменных, можно из системы (6) найти остальные n — переменных. Будем исходить из заданного ассортиментного вектора У = (y1, y2,…, yn) и определять необходимый для его производства вектор-план Х = (х1, х2,… хn). Проиллюстрируем вышеизложенное на примере предельно упрощенной системы, состоящей из двух производственных отраслей: Пусть исполнение баланса за предшествующий период характеризуется данными, помещенными в табл. 2 Рассчитываем по данным этой таблицы коэффициенты прямых затрат: Эти коэффициенты записаны в табл. 2 в углах соответствующих клеток. Теперь может быть записана балансовая модель (6), соответствующая данным табл. 2 х1 — 0.2х1 — 0.4х2 = у1 х2 — 0.55х1 — 0.1х2 = у2 Эта система двух уравнений может быть использована для определения х1 и х2 при заданных значениях у1 и у2, для использования влияния на валовой выпуск любых изменений в ассортименте конечного продукта и т.д. Так, например, задавшись у1=240 и у2=85, получим х1=500 и х2=400, задавшись у1=480 и у2=170, получим х1=1000 и х2=800 и т.д. Решение балансовых уравнений с помощью обратной матрицы Вернемся снова к рассмотрению балансового уравнения. 3 Первый вопрос, который возникает при его исследование, это вопрос о существование при заданном векторе У0 неотрицательного решения х0, т.е. о существовании вектор-плана, обеспечивающего данный ассортимент конечного продукта У. Будем называть такое решение уравнения (6′) допустимым решением. Заметим, что при любой неотрицательной матрице А утверждать существование неотрицательного решения нельзя. Так, например, если Сложив эти два уравнения почленно, получим уравнение -0.5х1 — 0.7х2 = у1 + у2, которое не может удовлетворяться неотрицательным значениям х1 и х2, если только у10 и у20 (кроме х1=х2=0 при у1=у2=0). Наконец уравнение вообще может не иметь решений (система (6) — несовместная) или иметь бесчисленное множество решений (система (6) — неопределенная). Следующая теорема, доказательство которой мы опускаем, дает ответ на поставленный вопрос. Теорема. Если существует хоть один неотрицательный вектор х0, удовлетворяющий неравенству (Е — А)·х0, т.е. если уравнение (6′) имеет неотрицательное решение x0, хотя бы для одного У0, то оно имеет для любого У0 единственное неотрицательное решение. При этом оказывается, что обратная матрица (Е — А) будет обязательно неотрицательной. Из способа образования матрицы затрат следует, что для предшествующего периода выполняется равенство (Е — А)·х’ = У’, где вектор-план х’ и ассортиментный вектор У’ определяются по исполненному балансу за прошлый период, при этом У’0. Таким образом, уравнение (6′) имеет одно неотрицательное решение x0. На основании теоремы заключаем, что уравнение (6′) всегда имеет допустимый план и матрица (Е — А) имеет обратную матрицу. Обозначив обратную матрицу (Е — А) — 1 через S = || sik+ ||, запишем решение уравнения (6») в виде Если будет задан вектор — конечный продукт У и вычислена матрица S = (E — A) — 1, то по этой формуле может быть определен вектор-план х. Полные внутрипроизводственные затраты Выясним экономический смысл элементов Sik матрицы S. Пусть производится только единица конечного продукта 1-й отрасли, т.е. Чтобы выпустить только единицу конечного продукта k-й отрасли, необходимо в 1-й отрасли выпустить х1=S1k, во 2-й х2=S2k и т.д., в i-й отрасли выпустить xi=Sik и, наконец, в n-й отрасли выпустить xn=Snk единиц продукции. 4 Так при этом виде конечного продукта производства только единица k-го продукта, то величины S1k, S2k,…, Sik,…, Snk, представляют собой коэффициенты полных затрат продукции 1-й, 2-й и т.д., n-й отраслей идущей на изготовление указанной единицы k-го продукта. Мы уже ввели раннее коэффициенты прямых затрат a1k, a2k,…, aik,…, ank на единицу продукции k-й отрасли, которые учитывали лишь ту часть продукции каждой отрасли, которая потребляется непосредственно k-й отраслью. Но, очевидно, необходимо обеспечить замкнутый производственный цикл. Если бы продукция i-й отрасли поступала бы только в k-ю отрасль в количестве aik, то производство k-й отрасли все равно не было бы обеспеченно, ибо потребовалось еще продукты 1-й отрасли (a1k), 2-й отрасли (a2k) и т.д. А они в свою очередь не смогут работать, если не будут получать продукцию той же i-й отрасли (ai1, ai2,… и т.д.). Проиллюстрируем сказанное на примере табл. 2 Пусть нас не интересует выпуск для внешнего потребления продукции 2-й отрасли (k=2) и мы хотим определить затраты продукции 1-й отрасли на единицу этой продукции. Из табл. 2 находим, что на каждую единицу продукции 2-й отрасли (х2=1) затрачивается: продукции 1-й отрасли a12=0.4 и 2-й отрасли a22=0.1. Таковы будут прямые затраты. Пусть нужно изготовить у2=100. Можно ли для этого планировать выпуск 1-й отрасли х1=0.4100=40 — Конечно, нельзя, т.к. необходимо учитывать, что 1-я отрасль часть своей продукции потребляет сама (а11=0.2), и поэтому суммарный ее выпуск следует скорректировать: х1=40+0.240=48. Однако и эта цифра неверна, т.к. теперь уже следует исходить из нового объема продукции 1-й отрасли — х1’=48 и т.д. Но дело не только в этом. Согласно табл. 2 продукция 2-й отрасли также необходима для производства и 1-й и 2-й отраслей и поэтому потребуется выпускать больше, чем у2=100. Но тогда возрастут потребности в продукции 1-й отрасли. Тогда достаточно обратиться к составленной систем уравнений, положив у1=0 и у2=1 (см п. 2): Решив эту систему, получим х1=0.8 и х2=1.5. Следовательно, для того чтобы изготовить единицу конечного продукта 2-й отрасли, необходимо в 1-й отрасли выпустить продукции х1=0.8. Эту величину называют коэффициентом полных затрат и обозначают ее через S12. Таким образом, если а12=0.4 характеризует затраты продукции 1-й отрасли на производство единицы продукции 2-й отрасли, используемые непосредственно во 2-й отрасли (почему они и были названы прямые затраты), то S12 учитывают совокупные затраты продукции 1-й отрасли как прямые (а12), так и косвенные затраты, реализуемые через другие (в данном случае через 1-ю же) отрасли, но в конечном счете необходимые для обеспечения выпуска единицы конечного продукта 2-й отрасли. Эти косвенные затраты составляют S12-a12=0.8-0.4=0.4 Если коэффициент прямых затрат исчисляется на единицу валового выпуска, например а12=0.4 при х2=1, то коэффициент полных затрат рассчитывается на единицу конечного продукта. 5 Итак, величина Sik характеризует полные затраты продукции i-й отрасли для производства единицы конечного продукта k-й отрасли, включающие как прямые (aik), так и косвенные (Sik — aik) затраты. Рассмотренные теоретические вопросы и примеры расчета, конечно, далеко не исчерпывают важную для практики область балансовых исследований. Здесь проиллюстрировано только одно направление приложения линейной алгебры в экономических исследованиях. ГЛАВА 2. Решение балансовых уравнений с помощью обратной матрицы Первый вопрос, который возникает при его исследование, это вопрос о существование при заданном векторе У>0 неотрицательного решения х>0, т.е. о существовании вектор-плана, обеспечивающего данный ассортимент конечного продукта У. Будем называть такое решение уравнения ( 6′ ) допустимым решением. Заметим, что при любой неотрицательной матрице А утверждать существование неотрицательного решения нельзя. Так, например, если 0.9 0.8 0.1 -0.8 и уравнение ( 6′ ) А= , то Е — А = 0.6 0.9 -0.6 0.1 запишется в виде 0.1 -0.8 х1 у1 или в развернутой форме -0.6 0.1 х2 у2 0.1х1 — 0.8х2 = у1 ( a ) -0.6х1 + 0.1х2 = у2 Сложив эти два уравнения почленно, получим уравнение -0.5х1 — 0.7х2 = у1 + у2, которое не может удовлетворяться неотрицательным значениям х1 и х2, если только у1>0 и у2>0 ( кроме х1=х2=0 при у1=у2=0 ). Наконец уравнение вообще может не иметь решений ( система ( 6 ) – несовместная ) или иметь бесчисленное множество решений ( система ( 6 ) – неопределенная ). Следующая теорема, доказательство которой мы опускаем, дает ответ на поставленный вопрос. Теорема. Если существует хоть один неотрицательный вектор х>0, удовлетворяющий неравенству ( Е — А )·х>0, т.е. если уравнение ( 6′ ) имеет неотрицательное решение x>0, хотя бы для одного У>0, то оно имеет для любого У>0 единственное неотрицательное решение. При этом оказывается, что обратная матрица ( Е — А ) будет обязательно неотрицательной. Из способа образования матрицы затрат следует, что для предшествующего периода выполняется равенство ( Е -А )·х’ = У’, где вектор-план х’ и ассортиментный вектор У’ определяются по исполненному балансу за прошлый период, при этом У’>0. Таким образом, уравнение ( 6′ ) имеет одно неотрицательное решение x>0. На основании теоремы заключаем, что уравнение ( 6′ ) всегда имеет допустимый план и матрица ( Е — А ) имеет обратную матрицу. Обозначив обратную матрицу ( Е — А )-1 через S = || sik+ ||, запишем решение уравнения ( 6» ) в виде х = S·У ( 7 ) Если будет задан вектор – конечный продукт У и вычислена матрица S = ( E — A )-1, то по этой формуле может быть определен вектор-план х. Решение ( 7 ) можно представить в развернутой форме: x1 = S11y1 + S12y2 + … + S1nyn x2 = S21y1 + S22y2 + … + S2nyn ( 8 ) ……………………………… xn = Sn1y1 + Sn2y2 + … + Snnyn И так сделаем выводы по данной работе балансовая модель производства является одной из наиболее простых математических моделей. Она записывается в виде системы уравнений, каждое из которых выражает требование равенства (баланса) между количеством продукции, производимой отдельным экономическим объектом, и совокупной потребностью в этом продукте. Под экономическим объектом обычно понимают так называемую «чистую прибыль». Например, чтобы правильно отразить взаимосвязи между машиностроением и металлургией, необходимо исключить продукцию металлургической и других отраслей из продукции машиностроения, а в продукции металлургической промышленности не учитывать произведенные на металлургических заводах продукты машиностроения и других отраслей. Таким образом, продукция «чистой отрасли» складывается из продукции специализированных предприятий, очищенной от непрофильных ее видов, и продукции, соответствующей профилю данной отрасли, но произведенной на предприятиях, относящихся к другим отраслям. 1 . А.Д. Черкай. Бухгалтерский и финансовый учет — язык бизнеса для руководителей. МСФО, US GAAP, РСБУ. Теория двух рядов 4-х счетов автора, новые балансовые уравнения и лингвистические модели учета. – М.: ПИК ВИНИТИ, 2015. – 120 с. Видео:Решение матричных уравненийСкачать  Матричная форма записи системы балансовых уравнений.Введем в рассмотрение векторы-столбцы объёмов произведенной продукции (вектор валового выпуска), объёмов продукции конечного потребления (вектор конечного потребления) и матрицу коэффициентов прямых затрат: Тогда система уравнений (3) в матричной форме имеет вид: Обычно это соотношение называют уравнением линейного межотраслевого баланса. Уравнение межотраслевого баланса можно использовать в двух целях. В первом, наиболее простом случае, когда известен вектор валового выпуска где E – единичная матрица той же размерности, что и матрица прямых затрат A. Во втором случае уравнение межотраслевого баланса используется для целей планирования со следующей формулировкой задачи: для периода времени Т (например, год) известен вектор конечного потребления где Если решение уравнения (4) существует, то матрица A называется продуктивной. 1. Матрица A продуктивна тогда и только тогда, когда матрица 2. Матрица A с неотрицательными элементами продуктивна, если сумма элементов по любому её столбцу или строке не превосходит единицы, причем хотя бы для одного столбца или строки эта сумма строго меньше единицы. ЗАДАЧА 1. Таблица (1) содержит данные баланса трех отраслей промышленности за отчетный период. Требуется: 1) Убедиться, что модель продуктивна, т.е. найти матрицу коэффициентов прямых затрат и убедиться в том, что она продуктивна; 2) Составить баланс производства и распределения продукции; 3) Найти конечный продукт (вектор конечного продукта 4) Найти валовой продукт (вектор валового выпуска
Решение. 1. Найдем матрицу коэффициентов прямых затрат. Из (1) Получим следующую матрицу прямых затрат:
2. Проверка продуктивности матрицы прямых затрат. Для проверки используем второй критерий. Для этого вычисляем суммы элементов в строках и столбцах. Результаты приведены в таблице (2). Поскольку все суммы элементов и в столбцах и в строках меньше единицы, то матрица продуктивна. Исходя из этого можно утверждать, что для неё существует обратная матрица с положительными коэффициентами. 3. Составим баланс производства и распределения продукции. Модель баланса производства и распределения продукции отрасли можно представить следующей системой уравнений: 4. Найдем матрицу полных затрат Каждый элемент матрицы B рассчитывается по формуле где Aij— алгебраические дополнения элементов матрицы (E-A); D- определитель матрицы (E-A). Определитель матрицы (E-A): Расчет алгебраических дополнений матрицы (E-A) дает следующие результаты: Составим матрицу B: Замечание. Поскольку матрица A продуктивна, то все коэффициенты матрицы полных затрат должны быть положительны. Отрицательные значения будут свидетельствовать об ошибке в расчетах. 5. Вычисление нового конечного продукта (вектора конечного продукта) при измененном валовом выпуске: 6. Вычисление нового валового продукта (вектора валового выпуска) при измененном конечном потреблении: Видео:Решение системы уравнений методом обратной матрицы.Скачать  Решение балансовых уравнений с помощью обратной матрицыАвтор: anastasiya343 • Июнь 15, 2018 • Реферат • 3,093 Слов (13 Страниц) • 903 Просмотры Глава 1.Понятие матрицы. Матричные уравнения. Обратная матрица 5 Глава 2. Основные понятия, связанные с балансовыми уравнениями 10 Глава 3. Балансовые модели 16 Глава 4. Решение балансовых уравнений с помощью обратной матрицы 22 Список использованной литературы и источников 25 Основой развития общества является процесс расширенного воспроизводства, осуществляемый хозяйствующими субъектами в различных сферах материального производства, выполнения работ и оказания услуг. Организация процессов производствами продажи продукции, выполнения работы передачи их результатов заказчикам, а также оказания услуг предполагает необходимость оценки результатов деятельности организации или индивидуального предпринимателя, состояния счетов, с одной стороны, с поставщиками материально-производственных запасов, подрядчиками, выполняющими работы и услуги, с другой стороны, — с покупателями товаров или продукции, заказчиками работ и услуг. Обобщение информации об объемах и результатах деятельности отдельных организации и индивидуальных предпринимателей требуется для государственного и регионального регулирования экономики. Обработка такой информации позволяет определить тенденции развития отдельных отраслей и видов производств, определить необходимость государственной поддержки или, напротив, изъятия части дифференциальной ренты, получаемой участниками предпринимательской деятельности. Хорошее знание теории учета имеет первостепенное значение для формирования профессиональной подготовки и деловых качеств многих специалистов. Большая часть математических моделей экономических объектов, а также процессов записывают в матричной форме, простой и компактной. Понятие матрицы в математике берет свое начало еще из 19 века. Изучение же балансовых моделей представляющих собой одно из важнейших направлений в экономико-математических исследованиях, должно служить объектом изучения отдельной дисциплины. В нашей работе мы разберем в теории и на практике определенные вопросы, связанные с решение балансовых уравнений с помощью обратной матрицы. Важно понять, что же такое матрица в математике, что такое баланс в области бухгалтерского учета, в данном случае, и как с помощью матриц решить уравнение баланса. Каждая глава этой работы представляет собой отдельную тему, начиная с теоретических данных и заканчивая практическим примером. При подготовке данного реферата использовались положения учебных изданий ученых в области математики, экономики и теории бухгалтерского учета, таких как Н.Ш.Кремер, С.А.Розанова, Б.Т.Кузнецов, И.А.Пономаренко, С.В.Булгакова, Н.Г. Сапожникова, Климович Л.П., Ивакина И.И., В.В.Федосеев и др. 🔍 ВидеоРешение системы уравнений методом обратной матрицы - bezbotvyСкачать  Решение системы уравнений методом Крамера.Скачать  9. Метод обратной матрицы для решения систем линейных уравнений / матричный методСкачать  Математика без Ху!ни. Метод Гаусса.Скачать  Решение систем линейных уравнений с помощью матрицСкачать  Матричный метод решения систем уравненийСкачать  Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать  Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать  §29 Решение матричного уравненияСкачать  Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать  Решение системы уравнений методом ГауссаСкачать  Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать  Лекция 8. Решение матричных уравненийСкачать  6 способов в одном видеоСкачать  Модель межотраслевого баланса. Часть 1 ТеорияСкачать  Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать  Обратная матрицаСкачать  |
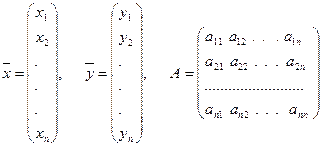
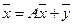 (4)
(4)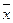 , требуется рассчитать вектор конечного потребления
, требуется рассчитать вектор конечного потребления 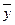 : из (4) следует, что
: из (4) следует, что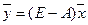 ,
,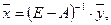
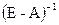 обратная матрица. Она называется матрицей полных затрат.
обратная матрица. Она называется матрицей полных затрат.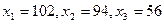 , а новые значения вектора валового выпуска
, а новые значения вектора валового выпуска 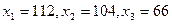 ;
;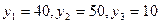 , а новые значения вектора конечного продукта
, а новые значения вектора конечного продукта 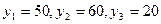 .
.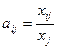
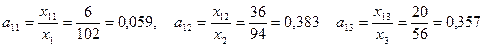 и т.д.
и т.д.
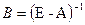
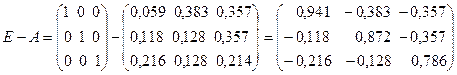
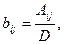
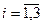 ;
; 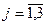 ,
,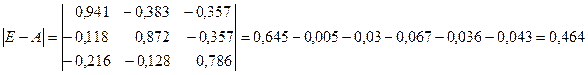

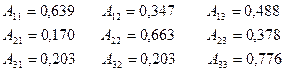
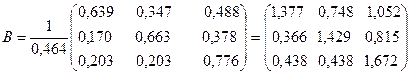

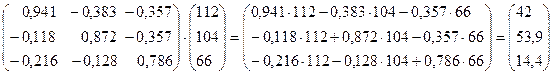
 — конечный продукт машиностроения,
— конечный продукт машиностроения,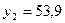 — конечный продукт ракетостроения,
— конечный продукт ракетостроения,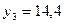 — конечный продукт нефтехимии.
— конечный продукт нефтехимии.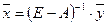 .
.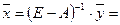
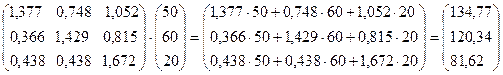
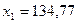 — валовая продукция машиностроения,
— валовая продукция машиностроения,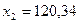 — валовая продукция ракетостроения,
— валовая продукция ракетостроения,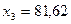 — валовая продукция нефтехимии.
— валовая продукция нефтехимии.