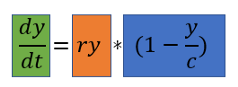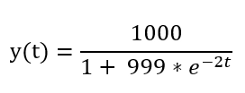Описание k и r стратегии исходя из уравнения логистического роста

В прошлой статье мы рассмотрели пример моделирования первой вспышки коронавируса с помощью экспоненциального роста. Следующая ступень анализа — логистический рост. Воспользуйтесь Python notebook и данными для примера, чтобы начать практиковаться уже сейчас.

Почему именно логистический рост?

Логистический рост — это математическая функция, которая может использоваться в нескольких ситуациях. Логистический рост характеризуется увеличением роста в начальный период, но снижением на более поздней стадии, при приближении к максимуму. В случае с коронавирусом этот максимальный предел будет равен общему количеству людей в мире, потому что, когда все заболеют, рост неизбежно уменьшится.

В других случаях использования логистического роста числом максимум может быть размер популяции животных, растущей в геометрической прогрессии до момента, когда среда обитания не сможет обеспечить достаточное количество пищи для всех животных. Далее, рост замедляется до тех пор, пока не будет достигнута максимальная емкость среды.

Причиной использования экспоненциального роста для моделирования вспышки коронавируса является то, что, согласно исследованиям специалистов, первая вспышка эпидемии следует принципу экспоненциального роста, а общий период эпидемии — принципу логистического роста.

Формула логистического роста

Логистический рост характеризуется следующей формулой:

• y (t) — количество случаев в любой момент времени t;
• c — предельное значение, максимальная емкость для y;
• b(фактор роста) должен быть больше 0.

Также отметим два других очень интересных момента об этой формуле:

• начальное значение равно: c / (1 + a);
• максимальная скорость роста при t = ln (a) / b и y (t) = c / 2.

Глубокое погружение в формулу логистического роста для любителей математики

Для тех, кто хочет лучше понять математическое значение формулы: приведенная выше функция фактически получена из приведенной ниже дифференциальной формулы, обнаруженной Пьером Франсуа Ферхюльст. Я объясню её пошагово:

• Выделенная зеленым часть dy / dt указывает, что эта формула предназначена для расчета роста, а не численности населения.
• Мы видим, что у и с находятся в формуле, значит рост населения зависит от численности населения (у) и от максимальной емкости (с).
• Когда y равно c (то есть население имеет максимальный размер), y / c будет равно 1. Следовательно, выделенный синим множитель будет равен 0 и рост, соответственно, будет равен 0.
• Когда у намного меньше, чем с (популяция находится далеко от предела), выделенная синим часть будет приблизительно равна 1. Следовательно, рост определяется частью ry, выделенной оранжевым. Оранжевая часть — это формула экспоненциального роста.

Простой пример логистического роста

Для ясности, рассмотрим гипотетический пример, в котором:

• максимальное количество больных людей с составляет 1000;
• мы начинаем с начального значения, равного 1 (первый зараженный человек), поэтому c / (1 + a) = 1, даёт 1000 / (1 + a) = 1, где а= 999;
• в начале инфекции каждый больной заражает 2 других людей, поэтому скорость роста b = 2;
• мы будем проверять развитие эпидемии от 0 до 10.

Сначала подставляем значения a и b в формулу, чтобы получить формулу для нашей конкретной эпидемии:

В Python это выглядит следующим образом:

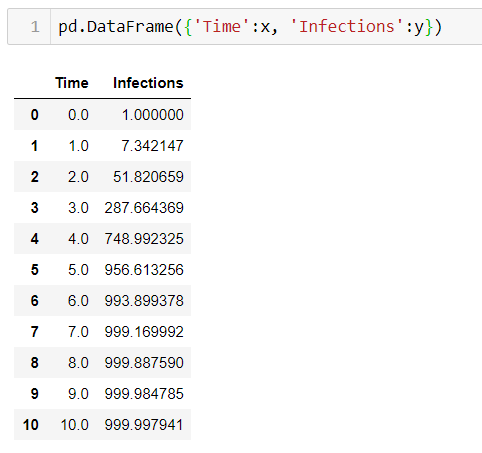
Далее мы используем эту формулу, чтобы вычислить значение y для каждого значения t от 0 до 10. В результате, мы получим число зараженных людей в каждый промежуток времени, как видно из таблицы ниже. Это показывает, что в начале наблюдается быстрый рост числа инфекций, но затем его темпы замедляются и рост заканчивается на максимальной емкости .

В графическом представлении мы получаем кривую, очень напоминающую реальные визуализации вспышки коронавируса:

От данных о коронавирусе к формуле логистического роста

Чтобы найти реальную кривую роста эпидемии коронавируса, рассмотрим данные о распространении вируса. Воспользуемся данными из Китая: поскольку рост там уже сильно снизился, это дает нам возможность получить подходящую логистическую кривую.

Нелинейная оценка наименьших квадратов для логистического роста коронавируса в Китае

Эти данные предоставляют информацию исключительно о количестве случаев в день. Чтобы успешно применить формулу логистического роста, нам необходимо получить правильные значения параметров a, b и c.

К сожалению, невозможно представить логистическую функцию в форме линейной регрессии, как это было в случае модели экспоненциального роста. Поэтому нам понадобится более сложный метод: нелинейная оценка наименьших квадратов.

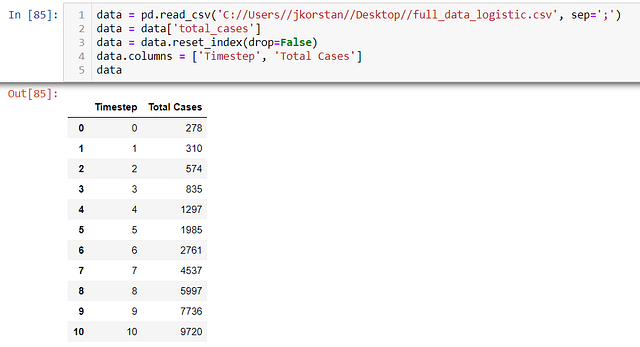
ШАГ 1 — “Читаем” данные:

ШАГ 2 — Определяем соответствующую логистическую функцию:

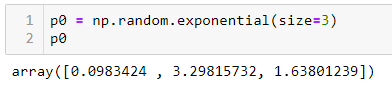
ШАГ 3 — Произвольно инициализируем a, b и c:

Мы инициализировали np.random.exponential, но вы можете использовать все что угодно. Внимание: ваш выбор может повлиять на результат шага 5.

ШАГ 4 — Устанавливаем верхнюю и нижнюю границы для a, b и c:

Нижние границы для всех параметров равны 0. Я установил верхнюю границу для b на 3, потому что с первой попытки я задал её произвольно, и она стала слишком высокой. Верхние границы a и c не оказали отрицательного влияния на подгонку кривой, поэтому я установил сравнительно высокие границы для этих переменных.

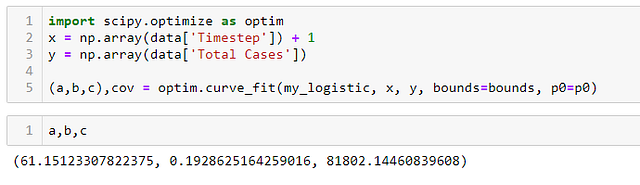
ШАГ 5 — Используем Scipy Curve Fit для нелинейной оценки наименьших квадратов:

На этом этапе Scipy выполняет оптимизацию нелинейных наименьших квадратов и дает нам значения для a, b и c, которые минимизируют ошибку наименьших квадратов нашей модели.

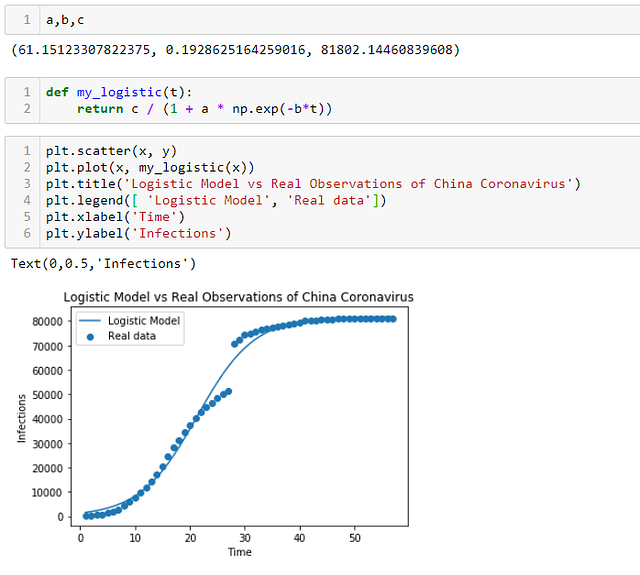
ШАГ 6 — Сравниваем на графике кривые полученной функции и реальных данных:

Как вы можете видеть на графике ниже, логистическая модель действительно не так уж далека от реальных данных распространения коронавируса в Китае.

ШАГ 7 — Заключение:

Мы определили, что логистическая функция по форме действительно очень близка к наблюдаемым данным распространения коронавируса в Китае. Чтобы применять эту информацию в реальной жизни, необходимо выполнить много проверок моделей, сравнить точность и другие показатели производительности различных моделей, а также внимательно следить за тем, будут ли будущие тенденции распространения вируса следовать сценарию выбранной модели.

Это выходит за рамки этой статьи, которая просто пытается показать, как определить кривую логистического роста. Тем не менее, теоретически, мы можем сформулировать некоторые наблюдения:

• Согласно этой модели, c составляет 81 802, предсказывая максимальный предел для числа инфекций в Китае, который составит 81 802 случаев.

Согласно этой модели, также можно вычислить момент, когда скорость роста достигла максимального значения:

• это был момент времени: t = ln (a) / b = ln (61,5) / 0,1929 = 21-й день;
• число инфекций в этот момент составило: у = с / 2 = 40 500.

В случае если эта модель будет тщательно проверена и верифицирована, она может быть использована законодателями для оценки принятых и определения правильных мер.

Надеемся, что наш пример прояснил вам процесс определения логистической модели и ее применение для различных ситуаций. Благодарим за чтение!

Видео:Логист | Профессия логист | Логистика | Что нужно знать начинающему логистуСкачать

Модели роста популяций: модель Ферхюльста (логистический рост), модель с наименьшей критической численностью.

1 СЕМИНАР Модели роста популяций: модель Ферхюльста (логистический рост), модель с наименьшей критической численностью. ЛОГИСТИЧЕСКИЙ РОСТ (УРАВНЕНИЕ ФЕРХЮЛЬСТА) Частым явлением в природе является ограниченность ресурсов (пищевых, территориальных) и, как следствие, внутривидовая конкуренция. Как правило, если численность популяции очень мала, то конкуренция не влияет на удельную скорость роста популяции r. Когда же численность возрастает и приближается к некоторому предельному значению, удельная скорость роста падает до нуля. Предельное значение называется емкостью экологической ниши популяции. Величина К соответствует такой численности популяции, при которой фактическая скорость воспроизводства в результате конкуренции настолько снижена, что популяция в целом может только восстанавливать в каждом поколении свою численность. В этот момент количество родившихся особей уравновешивается количеством погибших. Предположим, что зависимость удельной скорости роста популяции от ее численности линейна (рис. ). Получим уравнение dx() r = r x() (.) d x или dx() r = x() r x(). (. * ) d

2 Семинар. Модели роста популяций Рис. Простейшая линейная зависимость, иллюстрирующая снижение удельной скорости роста в связи с увеличением плотности популяции. Уравнение (. * ) получило название «уравнение логистического роста» или «уравнение Ферхюльста». Слагаемые в правой части уравнения (. * ) можно интерпретировать следующим образом. Удельная (средняя) скорость рождаемости есть некоторая положительная постоянная, не зависящая от времени и размера популяции x() (положительное слагаемое r). А удельная (средняя) смертность пропорциональна размеру популяции (отрицательное слагаемое x() r ). Увеличение смертности с ростом популяции может происходить благодаря эффектам скученности или усиливающейся конкуренции за доступные пищевые ресурсы. dx r Раскроем скобки в уравнении (. * ): = x r x. d Первое слагаемое будет нам давать информацию о неограниченном росте популяции. Второе о влиянии внутривидовой конкуренции (отрицательном влиянии взаи-

3 Учебное пособие «Математические модели в биологии» r модействия двух особей одного вида: x ) на скорость роста популяции. Исследуем уравнение логистического роста (уравнение Ферхюльста,. * ). Сначала находим стационарные значения численности популяции: r r x r x = x = или r x =. Получаем два стационарных значения x = и, x =. Будут ли эти стационарные состояния устойчивыми? Воспользуемся аналитическим методом Ляпунова. Согласно ему для определения устойчивости необходимо определить знак производной функции f ( x ), стоящей в правой части дифференциального уравнения, в точках x (подробный вывод см. в разделе Семинар ). Производная функция равна: r = = r f ( x) x r x r x Подставляем стационарные значения: r f ( x ) = r x = r. Показатель удельной скорости x= x = роста r есть положительная константа ( r > ), что означает неустойчивость стационарного состояния x =. Производная функции в точке x :. r f ( x) = r x = r. x= x = Величина r отрицательная, т.е. стационарное состояние x = является устойчивым.

4 Семинар. Модели роста популяций По какому закону будет изменяться во времени численность популяции x()? Для ответа на этот вопрос решим дифференциальное уравнение (.) методом разделения переменных. dx rd x ( x ) = (для сокращения записи вместо x() будем писать x, подразумевая, что численность x есть функция от времени); + dx = r d ; x ( x) ( ln ln( )) x x = r+ C (численность x есть положительная величина, поэтому при интегрировании знак модуля в выражении ln( x ) опускаем, C произвольная ‘ константа); x ln = r + C ; x x x x x = Ce r = Ce, C = e r. C ; Пусть в начальный момент времени численность равнялась x() = x. Определим величину константы C: x x = C. Получим окончательную формулу зависимости численности популяции от времени: x () x = x() x e r или r xe x () =. (.) r x + x e 3

5 Учебное пособие «Математические модели в биологии» Знак модуля можно опустить, поскольку величины x и x() всегда одного знака (см. дальнейшее исследование). Построим график полученной зависимости (.) в области положительных значений времени. В начальный момент времени имеем x() = x. При + численность популяции стремится к величине емкости экологической ниши: x e x x = = = = r lim x( ) lim lim + + r x x + xe + + x x r e x (так как lim = ). + r e На графике существование этого предела отражается в наличии горизонтальной асимптоты x() =. r Знаменатель функции x() равен x + xe. Если r начальное значение x , знаменатель в ноль не обращается. При x > знаменатель обращается в ноль, когда as = ln. Аргумент лога- x r x рифма x x данном случае меньше, поэтому значение as меньше нуля. Таким образом, в случае x > в области отрицательных значений будет иметь место вертикальная асимптота as = ln x r x. 4

6 Семинар. Модели роста популяций Теперь исследуем первую и вторую производную функции (.), чтобы определить, есть ли у кривой, задаваемой этой функцией, экстремумы или перегибы: x () ( ) r ( x + xe ) ( ) r ( ) rxe x + xe xe rxe r r r r r xe = r = = x + x e x + x e rx e x = r. Производная x () > в случае x производная x () функция x() монотонно убывает и асимптотически стремится к величине. r rxe ( x ) x () = = r ( x+ xe ) ( ) ( ) ( ) ( ) ( ) r r r r r xe x x + xe rxe x x + xe = = r ( x + x e ) r ( )( + ) r 4 ( ) r ( x + x e ) r r x e x x x e r = x + xe xe = ( ) = r rxe x 3 r ( x + xe ) r ( x xe ). 4 5

7 Учебное пособие «Математические модели в биологии» В случае x > вторая производная в ноль не обращается, функция x() перегибов не имеет. Рассмотрим случай x , т.е. x , то p 8 Семинар. Модели роста популяций растать, пока численность не достигнет значения, а затем начнет снижаться, стремясь к нулю. Если начальная численность популяции составляет более половины емкости экологической ниши, то размер популяции будет увеличиваться, стремясь к значению, а скорость ее роста будет неуклонно снижаться. Изменение характера развития популяции (переход от возрастания скорости роста к снижению в точке x () = ) про- изошло до того, как исследователь начал за ней наблюдать (т.е. до момента времени = ). Если же размер популяции в начальный момент времени больше предельно возможного значения, то численность популяции будет снижаться (рис..). x() x x x p p Рис. График решения логистического уравнения. 7

9 Учебное пособие «Математические модели в биологии» МОДЕЛЬ ПОПУЛЯЦИИ С НАИМЕНЬШЕЙ КРИТИЧЕСКОЙ ЧИСЛЕННОСТЬЮ В рассмотренной модели прирост численности популяции представлен линейным членом rx(). Строго говоря, это применимо лишь к тем видам, размножение которых происходит путем деления или самооплодотворения. Если же размножение предполагает скрещивание разнополых особей, то прирост будет тем выше, чем больше количество встреч между особями. Тогда для разнополой популяции прирост численности должен выражаться квадратичным членом rx (). При большой численности в популяции лимитирующим фактором становится количество половозрелых самок в популяции. Кроме того, важно учесть время, в течение которого может состояться оплодотворение. Если это время больше времени, в течение которого особь способна к размножению, то популяция вымирает. Уравнение, учитывающее фактор разнополости и количество самок, готовых к оплодотворению, имеет вид dx() β[ x()] = α. Учитывая смертность, пропорциональd β + τ x() cp Пусть Т среднее время между двумя последующими оплодотворениями, τ среднее время вынашивания плода, постоянное для каждого вида, cp среднее время, в течение которого может состояться оплодотворение: cp = T τ. Вероятность встречи, ведущей к оплодотворению, тем больше, чем больше соотношение cp T. Тогда коэффициент размножения для разнополых популяций r, можно представить в виде: cp cp r = α = α T + τ, где α коэффициент пропорциональности; cp величина, уменьшающаяся при возрастании плотности популяции: β = cons. Тогда, dx() cp x() x β β = α = α x = α x d + τ β x() + τ β + τx() cp cp β =, x() [ ( )] [ ( )] [ ( )]. 8

10 Семинар. Модели роста популяций ную численности популяции с коэффициентом γ, получаем уравнение: dx() [ x()] x() d = β α γ β + τx(). (.3) Уравнение (.3) имеет два стационарных значения: x = и x = γβ L αβ γτ = (значения параметров модели задаются такими, чтобы величина L была положительной). Исследуем устойчивость стационарных состояний графическим методом. Для этого необходимо определить знак β x x функции f( x) = α γx= (( αβ γτ) x γβ). Знаменатель функции положителен при положительных значе- β + τx β + τx ниях x, меняет знак при прохождении через значение β x =. Числитель меняет знак при прохождении через τ стационарные точки x,. В результате имеем f( x ) > при dx x > x = L, в области 11 Учебное пособие «Математические модели в биологии» численность (плотность). Она индивидуальна для каждого вида. График зависимости численности популяции, описываемой моделью (.3) от времени представлен на рис..3 б. fx ( )= dx d а x() б L x = x =L x Рис..3. Модель популяции с наименьшей критической численностью. Зависимость скорости роста популяции от ее размера (а) и динамика численности популяции (б). Учтем в модели (.3) важный фактор внутривидовой конкуренции. В этом случае получим общий закон, описывающий динамику разнополой популяции в условии ограничения ресурсов: dx() [ x()] x x d = β α γ δ β + τx() () [ ()]. Уравнение имеет три стационарных значения: (.4) βx x = α γx δx = ( αβx γ( β+ τx) δx( β+ τx) ) = β+ τx β+ τx x = ( δτ x + x( αβ γτ βδ ) γβ ). β+ τx Это нулевое решение x =, а также два значения, обращающих в ноль квадратный трехчлен: x ˆ = L и x ˆ 3 =. Значения численности ˆL и ˆ являются критическими: 3

12 Семинар. Модели роста популяций x ˆ = L минимально возможная численность, x ˆ 3 = максимально возможная (параметры модели α, β, τ, γ, δ выбирают такими, чтобы величины ˆL и ˆ были положительными). Устойчивость стационарных состояний проверим, аналогично предыдущему случаю, графическим dx x методом. Функция f ( x) = ( x Lˆ)( x ˆ) d = β + τx модели (.4) в положительной области значений переменной x меняет знак с «плюса» на «минус» при переходе через x = (это стационарное значение устойчиво), затем с «минуса» на «плюс» в точке x ˆ = L (неустойчивое стационарное значение) и, наконец, опять с «плюса» на «минус» в точке x ˆ 3 = (устойчивое стационарное значение) (рис..4 а). График зависимости численности популяции, описываемой моделью (.4) от времени представлен на рис..4 б. fx ( )= dx d а ˆ x() б ˆ L ˆ x = x =L x 3 = x ˆ Рис..4. Модель популяции с нижней и верхней критическими границами численности. Зависимость скорости роста популяции от ее размера (а) и динамика численности популяции (б). 3

13 Учебное пособие «Математические модели в биологии» ЗАДАЧИ К СЕМИНАРУ.. График функции, задающей скорость изменения численности микробной популяции, имеет вид: а б ) Какое выражение будет описывать динамику роста культуры, если в начальный момент времени ее размер равен 5. ) Какова будет численность культуры через час, если ее размер в начальный момент времени равна 7. Рост популяции описывается уравнением Ферхюльста. Емкость экологической ниши для нее равна. Постройте график динамики численности популяции, если известно, что начальная численность равна: а) ; б) 7; в). Скорость роста r равна.5. Укажите координаты точки перегиба и асимптоты..3. Рост популяции описывается уравнением, учитывающим нижнюю границу численности и внутривидовую dx x конкуренцию: = dx px. Определите величины d + x верхней и нижней границы численности, если известно, что коэффициент смертности равен., а внутривидовой конкуренции равен.4. Постройте графики динамики численности популяций для начальных значений меньших нижней критической границы, лежащих в пределах между нижней и верхней границей, и превышающих верхнюю границу. 3

14 СЕМИНАР 3 Дискретные модели популяций с неперекрывающимися поколениями. Дискретное логистическое уравнение. Лестница Ламерея. Модели, основанные на аппарате дифференциальных уравнений, применимы для описания динамики достаточно многочисленных популяций (например, микробных), у которых процессы рождения и гибели особей можно считать непрерывными, или у которых нет ярко выраженной сезонности периодов размножения. Если же мы имеем дело с организмами, для которых сезонность важная характеристика их жизненного цикла, то для описания динамики популяций таких видов более адекватным является аппарат конечно-разностных уравнений. Пусть численность некоторого вида в начальный момент времени равна N, по окончании одного периода времени N, по окончании двух N и.т.д. Развитие популяции во времени тогда описывается последовательностью чисел N, N, N, N, N +,. Разностным уравнением называется уравнение, которое связывает между собой значения N при различных значениях индекса. В общем виде численность популяции в определенный период времени зависит от численности на определенном предшествующем отрезке времени. В этом случае разностное уравнение имеет вид (. ) N = F N N N. (3.) n 33

15 Учебное пособие «Математические модели в биологии» + Параметры функции F в общем случае могут зависеть от конкретного периода времени. В простейшем случае, параметры среды обитания остаются неизменными, и мы приходим к уравнению с постоянными коэффициентами в правой части уравнения. Рассмотрим простую модель роста популяции, когда скорость роста в любой период времени пропорциональна размеру популяции в начале этого периода. Пусть N размер популяции в конце -го периода времени. Тогда величина N+ N выражает прирост популяции за следующий период времени, т.е. скорость роста, или рост в единицу времени, на ( + ) -м интервале времени. Эта величина должна быть пропорциональна численности N. Пусть коэффициент пропорциональности есть некоторая константа r, тогда получим разностное уравнение: N N = + rn или N+ = N( r+ ). Заметим, что это уравнение можно получить, исходя из исследованного ранее дифференциального уравнения модели экспоненциального роста (см. Семинар ) dn = rn. Скорость dn есть отношение приращения численности к приращению времени (только в отличие от не- d d прерывного случая приращение не является бесконечно Δ N N+ N N+ N малой величиной): = =. Приходим к Δ ( + ) дискретному аналогу уравнения экспоненциального роста: N + N = rn или N = ( r+ ) N, где r коэффициент вос- производства популяции. В рассмотренном примере численность популяции в конце каждого периода времени зависит лишь от ее величины по окончании предыдущего периода и не зависит от более ранних значений. В общем виде, подобный вид взаимосвязи (каждое значение в последовательности за- 34

16 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея висит только от значения на предыдущем шаге) можно описать формулой (сравните с формулой (3.)): N = или N F( N ) F( N ) =. (3.). + С помощью уравнения вида (3.) можно описывать популяции с неперекрывающимися поколениями. Например, для многих видов насекомых характерна непродолжительная жизнь взрослых особей. Взрослые особи откладывают яйца и погибают. К моменту выхода нового поколения, предыдущее поколение прекращает свое существование. К разностным уравнениям применимы понятия, используемые в теории дифференциальных уравнений. Решением (траекторией) дискретного уравнения называется любая последовательность значений ( =. ), удовлетворяющая данному дискретному уравнению при каждом значении времени, на котором уравнение определено. Различным начальным условиям соответствуют разные решения. Устойчивость решений определяется аналогично устойчивости решения дифференциального уравнения. * Равновесием называют решение вида N = cons = N, удовлетворяющее соотношению N = F( N ). (3.3) * * Устойчивость точки равновесия так же можно определить по методу Ляпунова: если при достаточно малом начальном отклонении от положения равновесия система никогда не уходит от положения равновесия, то такое положение равновесия называют устойчивым, оно соответствует устойчивому стационарному режиму функционирования системы. 35

17 Учебное пособие «Математические модели в биологии» Как и в случае с дифференциальным уравнением, для исследования устойчивости решения дискретного уравнения применим линейный анализ. * Положим N = N + x, где x отклонение от положения равновесия. Линеаризуем уравнение (3.), разлагая правую часть дискретного уравнения в ряд по степеням x в окрестности положения равновесия: df N = N + x = F N + x + o( x ). ( ) * * + + dn * N = N Учитывая определение равновесия (3.3) и отбрасывая члены порядка x и выше, получаем закон, по которому будет развиваться заданное отклонение: x + df = x. (3.4) dn * N = N Соотношение (3.4) между величинами отклонения от точки равновесия x и x + представляет собой геометрическую df прогрессию, где знаменатель прогрессии. Из dn * N = N условий сходимости геометрической прогрессии следует, что x при, если df dn * N = N , то заданное отклонение бу- 36

18 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея дет неограниченно расти: x при, и в этом случае положение равновесия будет неустойчивым. Случаи df dn * N = N = или требуют дополнительных исследований. df dn * N = N = Зная величину знаменателя геометрической прогрессии (3.4), можно сделать выводы о характере поведения траектории дискретного уравнения вблизи положения равновесия. Так, при положительных значениях знаменателя, все члены последовательности будут иметь оди- df наковый знак. Если монотонное удаление от него. При отрицательных значениях знаменателя, члены геометрической прогрессии становятся знакочередующимися. Если df 19 Учебное пособие «Математические модели в биологии» dn d ДИСКРЕТНОЕ ЛОГИСТИЧЕСКОЕ УРАВНЕНИЕ Формальная замена бесконечно малых приращений в дифференциальном уравнении логистического роста Δ N N N N N = = Δ ( + ) + + на Δ N N N rn N + = = Δ или дает следующий результат: N N+ = N + r. (3.5) N ( + r) Однако множитель + r при N > r становится отрицательным, уравнение (3.5) приводит к отрицательным значениям численности, что является с биологической точки зрения некорректным. Заметим, что в дифференциальном уравнении такого рода проблема отсутствует: множитель правой части N становится отрицательным при N >, но это дает отрицательную скорость размножения популяции (снижение размера популяции), а не отрицательную численность. Таким образом, необходимо модифицировать множитель правой части уравнения (3.5), сохранив следующие свойства: при малых значениях численности популяция растет и скорость роста не зависит от размера популяции; с течением времени численность популяции увеличивается, стремясь * к равновесному значению N =, а скорость роста стремится к нулю, оставаясь положительной. Таким свойст- r вом обладает выражение. Итак, получаем дискретный аналог логистического уравнения: e N 38

20 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея N r N N e + =. (3.6) Проведем исследование уравнения (3.6). Найдем положение равновесия: * * * N N e r N * * * * N = F( N ), т.е. =. Тогда N =, N Исследуем их устойчивость. В соответствии с аналитическим методом определения устойчивости необходимо определить знак и сравнить с величину производной правой части уравнения в точках равновесия. Производная функции равна: df dn N r = N e = N N r r r = e N e + = Nr N r = e. Подставляем значение df dn N = * N = : r r r = e = e >. =. Таким образом, при r >, состояние равновесия * N = неустойчиво, поведение траекторий в его окрестности монотонно. Подставляем значение df dn N = * N = : r r = e = r. 39

21 Учебное пособие «Математические модели в биологии» Условие df dn * N = N решение уравнения (3.6) неустойчиво. При этом, если r >, то решение немонотонно. Исследование модели логистического роста показало, что, в отличие от решения дифференциального уравнения, траектории, задаваемые его дискретным аналогом, при определенных значениях скорости прироста r обладают цикличностью, а также могут описывать различные хаотические режимы (так называемые вспышки численности). За ходом решения дискретного логистического уравнения можно проследить с помощью диаграммы (или лестницы) Ламерея. 4

22 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея ЛЕСТНИЦА ЛАМЕРЕЯ На рис. 3.. представлена зависимость численности популяции N + от численности на предыдущем шаге N, задаваемая логистическим уравнением (3.6): N r e ( ) N = N = + F N. Рис. 3.. График функции, задающей дискретное уравнение логистического роста (3.6). Пояснения в тексте. 4

23 Учебное пособие «Математические модели в биологии» N + Пунктирной линией представлена биссектриса = N. В точках пересечения графика функции F( N ) с биссектрисой выполняется равенство: N = N = + F( N), т.е. выполняется определение точки равновесия. Таким образом, точки пересечения графиков N (с координата- * ми (,)) и N (с координатами (К,К)) являются точками равновесия (см. предыдущий подраздел). * ШАГ. Пусть известна некоторая начальная численность популяции N. Какую последовательность следующих значений численностей задает логистическое уравнение? Значение N определяется равенством N = F( N), т.е. пара значений ( N, N ) является координатами соответствующей точки на графике функции F( N ) (рис. 3. а). Отложим на координатной плоскости ( N, ) точки (, N ) и (, N ) (рис. 3. б). ШАГ. Следующее значение численности N определяется из соотношения N = F( N) (рис. 3. в). На графике, величина N из значения функции должна стать значением аргумента: проводим перпендикуляр от точки (, N ) до пересечения с биссектрисой, затем опускаем перпендикуляр до оси абсцисс N. ШАГ 3. Повторяем шаг. Теперь наша начальная точка точка N, значение численности N есть ордината точки на графике функции F( N ): ( N, F( N ) ) (рис а, б). 4

24 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея ШАГ 4. Повторяем шаг. Значение N переносим на ось абсцисс с помощью отражения от биссектрисы (рис. 3.3 в). ШАГ 5. Повторяем шаг. Следующее значение численности N 3 определяем как ординату точки на графике функции F: (, ( )) N F N (рис. 3.4 а, б). Продолжая повторять шаги построения лестницы Ламерея, получим последовательность значений численности популяции в разные моменты времени. В рассмотренном примере мы получили, что со временем численность в виде затухающих колебаний сходится к равновесному значению (рис , 3.7 в). Характер последовательности значений численности популяции, полученной при помощи лестницы Ламерея, может быть монотонным, циклическим, колебательным и хаотическим. Каким он будет, в каждом конкретном случае определяется формой кривой F( N ). В свою очередь, форму кривой определяют значения параметров функции F( N ) (скорость прироста r и емкость экологической ниши ). 43

25 Учебное пособие «Математические модели в биологии» а а б б в в Рис. 3.. Построение лестницы Ламерея. Рис Построение лестницы Ламерея. Продолжение. 44

26 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея а а б б в в Рис Построение лестницы Ламерея. Продолжение. Рис Построение лестницы Ламерея. Продолжение. 45

27 Учебное пособие «Математические модели в биологии» а а б б в в Рис Построение лестницы Ламерея. Продолжение. Рис Построение лестницы Ламерея. Окончание. 46

28 Семинар 3. Дискретные модели роста популяций. Лестница Ламерея ЗАДАЧИ К СЕМИНАРУ С помощью диаграммы Ламерея построить график динамики численности популяции, если зависимость N+ = f( N) имеет вид: а б в г 47

Видео:Стратегия бизнеса - ключевые понятия и этапыСкачать

К- и r-экологические стратегии

Численность естественных популяций не остается постоянной, даже если популяция вышла на уровень асимптоты (К) в логистической кривой. Чаще всего наблюдаются закономерные чередующиеся подъемы и спады численности волнообразного характера. В 40-х годах прошлого века русским ученым С.А. Северцовым проанализированы возможные типы динамики для млекопитающих, учитывающие продолжительность жизни, сроки полового созревания, плодовитость, подверженность эпизоотиям и истребление хищниками. Были выделены 7 разнообразных типов динамики, которые позднее Н.П. Наумов (по: Шилов, 2001) обобщил и свел в три фундаментальных типа динамики населения (рис. 5.11).

Рис. 5.11. Типы динамики по С.А. Ссверцову: I — стабильный;

II — лабильный; III — эфемерный

Стабильный тип характеризуется малыми амплитудами и длительными периодами колебаний численности (10-20 лет). Такой тип характерен для крупных животных с большой продолжительностью жизни, поздним наступлением половозрелости и низкой плодовитостью (копытные млекопитающие, китообразные, гоминиды, крупные орлы, некоторые рептилии).

Лабильный тип динамики отличается периодичностью хорошо выраженных амплитуд (численность меняется в десятки раз) с порядком 5-11 лет. Весьма характерны сезонные изменения, связанные с периодичностью размножения. Такой тип характерен для разных животных, но, как правило, для некрупных и с более коротким сроком жизни (до 10-15 лет), более ранним созреванием и более высокой плодовитостью. К этому типу относятся крупные грызуны, зайцеобразные, некоторые хищники, птицы, рыбы, насекомые с длинным циклом развития и др.

Эфемерный тип характеризуется резко неустойчивой численностью (смена массовых вспышек численности глубокими депрессиями). Численности популяций максимумов и минимумов различаются в согни раз, причем такие перепады могут совершаться очень быстро (иногда в течение сезона). Длина цикла составляет до 4-5 лет. Этот тип характерен для корогкоживущих (до 3 лет) с несовершенными механизмами адаптации и высокой смертностью, что компенсируется очень высокой плодовитостью (мелкие грызуны, многие насекомые с коротким жизненным циклом).

Все эти типы динамики численности отражают интегральный эффект всех форм взаимодействия вида с абиотическими и биотическими факторами среды и по своей сути — разные жизненные стратегии (Шилов, 2001).

Именно эта мысль легла в основу концепции экологических стратегий, разработанной Р. Мак-Артуром и Э. Уилсоном в 1967 году и получившей широкое признание в мире (по: Гиляров, 1990).

Суть концепции сводится к двум положениям:

• 1 — успешное выживание и размножение возможно при совершенствовании адаптированное™ и конкурентоспособности;
• 2 — интенсификация размножения (высокая плодовитость и сокращение сроков между пометами, быс трая смена особей) компенсирует высокую смертность особей и в критических ситуациях позволяет восстанавливать численность.

Эти два крайних типа среди множества разнообразных экологических стратегиях выживания популяций и были названы К-стратегией и г-страте- гией. Собственно константы К (экологическая емкость среды) и г (скорость удельного роста популяции) из уже хорошо известного нам логистического уравнения роста популяций дали основание Р. Мак-Артуру и Э. Уилсону выделить два типа естественного отбора, соответствующие двум экологическим стратегиям.

Одна из них — /’-стратегия — определяется отбором, направленным, прежде всего, на повышение скорости роста популяции в начальный период увеличения ее численности. Именно для начального периода характерна низкая плотность популяции и слабо выраженная конкуренция, что создает при отсутствии лимитирующих факторов условия ее быстрого роста.

Другая — /С-стратегия — характеризуется естественным отбором, направленным на повышение выживаемости и значения емкости среды в условиях уже стабилизировавшейся численности при возросшей сильной внутривидовой и межвидовой конкуренции.

По своему содержанию /^-стратегия — это «отбор на качество», а /—стратегия — «отбор на количество».

Виды, развивающиеся по этим двум экологическим стратегиям, называют К-стратегами и г-стратегами. Они характеризуются стабильным (и частично лабильным) и эфемерным (и частично лабильным) типами динамики соответственно.

Виды с /—стратегией очень легко осваивают территории с нестабильными условиями и отличаются высоким уровнем энергозатрат на размножение. Это виды с высоким биотическим потенциалом, но слабой конкурентоспособностью. Популяции таких видов, как правило, обладают низкой стабильностью (устойчивостью), быстрее и легче осваивают новые территории. Скорость размножения таких видов не зависит от плотности популяции.

Виды с ЛГ-страгегией лучше себя чувствуют в местообитаниях с насыщенной плотностью и относительно стабильными условиями, а большую часть энергии они тратят на повышение уровня выживаемости и конкурентоспособности. Как правило, эти относительно стабильные популяции, адаптированные к зрелым биоценозам (привязаны к своим территориям), неохотно и медленнее осваивают новые территории. Обладают высокой конкурентоспособностью. Скорость размножения таких видов зависит от плотности популяции.

Ю. Одум (1986) приводит два примера, иллюстрирующие действие двух указанных отборов. Сравниваются два вида растений по их продукции семян и максимальному репродуктивному усилию — амброзия <Ambrosia artemisifolia), принадлежащая к однолетним травянистым растениям и произрастающая на пустырях и недавно нарушенных местообитаниях, и зубянка (Dentaria laciniata) — травянистый многолетник, обитающий в относительно стабильном нижнем ярусе леса. Амброзия продуцирует примерно в 50 раз больше семян, чем зубянка, но при этом тратит большую часть энергии на размножение. Следовательно, амброзия — это /—стратег, а зубянка — ЛГ-стратег. Выживание амброзии в местах с нарушенной средой обеспечивается высоким биотическим потенциалом, позволяющим быстро восстанавливать потерю численности. Зубянка, наоборот, адаптирована к более стабильным условиям и характеризуется равновесной, без особых колебаний численностью в условиях острой конкуренции. Большую часть энергии это растение тратит на повышение уровня адаптации и конкурентоспособности.

Типы экологических стратегий как крайние варианты типов динамики населения С.А. Северцова, гем не менее, отнюдь не дискретны. Существует полный ряд переходов от r-стратегии к ^-стратегии, и каждый вид в своей адаптации к условиям существования и своему месту в биоценозе комбинирует принципы разных стратегий в различных сочетаниях (Шилов, 2001).

Американский ученый О. Солбриг (1971) описал случай встречаемости этих двух принципиально полярных стратегий у одного и того же вида одуванчика <Taraxacum officinale) (по: Одум, 1986). Это травянистое однолетнее растение имеет несколько линий с различными генотипами, контролирующими распределение энергии. Растения одной линии первыми занимают нарушенные местообитания и продуцируют много мелких рано созревающих семян, тратя на это значительную часть энергии (г-стратег). Растения другой линии встречаются в менее нарушенных местообитаниях и тратят большую часть энергии на рост листьев и стеблей, продуцируя значительно меньше поздносозревающих семян (А^-стратег). Если обе линии произрастают на хорошей почве, то более плодовитая линия затеняется более адаптированной (/^-стратегом).

Рассматривая г- и /С-стратегии, А.М. Гиляров (1990) замечает, что каждый вид испытывает некую комбинацию г- и /С-отбора, т.е. оставляемые отбором особи должны обладать как достаточно высокой плодовитостью, так и достаточно развитой способностью выжить при наличии конкуренции и пресса хищников. Но в природе за каждое приобретение приходится расплачиваться. Жесткие ограничения, накладываемые на каждый организм его морфофизиологическими особенностями, не позволят организму преуспеть одновременно сразу по двум типам стратегий. Между количеством и качеством потомков приходится выбирать.

Как было показано выше, экологические стратегии присущи и растительным организмам. Особенность выбирать тот или иной путь стратегии была подмечена русским геоботаником Л.Г. Раменским в 1938 году. Будучи автором фундаментального экологического закона об экологической индивидуальности видов и теории экологического континуума, он также выделил три основных типа эколого-ценогических стратегий:

Виоленты — так называемые силовики. Эго конкурентоспособные виды, во многом определяющие облик фитоценозов. У них мощная корневая система и хорошо развитая надземная часть. Растения этой группы характеризуются высокой жизненностью и способностью быстро осваивать пространство. В эту группу включены многие деревья (например дуб, ель, береза) и доминирующие в тех или иных сообществах травянистые растения (мох сфагнум, тростник). Тростник может образовывать обширные заросли на мелководьях озер.

Патиенты — это выносливые растения, способные выживать в самых разных неблагоприятных условиях, где другие растения просто не могут существовать. К этой группе относят различные экологические группы — сухолюбивых, тенелюбивых (сциофитов), солелюбивых (многие кактусы, верблюжья колючка, баобаб, лебеда белая).

Эксплеренты — это виды «выполняющие» или захватчики. Они быстро размножаются и очень быстро расселяются даже в места с нарушенной средой. Л.Г. Раменский назвал их «шакалами растительного мира». Такие растения можно видеть на вырубках и гарях (иван-чай, осина, многие сорняки). При сук- цессионных процессах эксплеренты вытесняются виоленгами.

Концепция Л.Г. Раменского была развита известным английским ботаником Д. Граймом в 1979 году (по: Шилов, 2001), который сблизил ее с позициями г- и /^-стратегий.

По Грайму выделены следующие стратегии: конкурентная (= виоленты), стресс-толерантная (= патиенты), рудеральная (близка к экегшерентам).

Как и в случае со стратегиями для животного мира, растительные стратегии строго не детерминированы. Тип эколого-ценотических стратегий отражает не только аутэкологические характеристики вида, но и его положение в сообществе. Поэтому один и тот же вид, входя в разные сообщества, может относиться к разным типам стратегий. Например, сосна (Pinus silvestris) является типичным виолентом в сосновом бору, но в болотистых местообитаниях она становится патиентом (Гиляров, 1990).

📹 Видео

Стратегическое планирование и маркетинговая стратегияСкачать

Основы бизнес-стратегии для предпринимателейСкачать

Организация ВЭД на предприятии. Основные риски, экспортная стратегия и потенциал. СеминарСкачать

Офисный рынок 2022: от уравнения со множеством неизвестных к четкой стратегииСкачать

Понятие стратегииСкачать

Стратегический маркетингСкачать

Урок 1 - Обзор процесса стратегического планированияСкачать

Как подготовить рекламные кампании к новому году при помощи конверсионных стратегийСкачать

Выигрышная стратегия в теории игр | 8/50 урок Информатики | Задания 19-21 ЕГЭСкачать

Стратегия компании. Базовые принципы разработки. Примеры проектов | Арсений Кутовой | DotorgСкачать

Простой прогноз продаж в Excel с учетом сезонностиСкачать

Дизрапт/Disrupt: от случайного к серийному - Антон Еликов | CPO КонтурСкачать

ОТКЛОНЕНИЕ ДИАПАЗОНА - Лучший Вход и ВыходСкачать

Стратегии ценообразования в 2023 году: обзор стратегий и факторов влияния. Павел Смирнов, ПолиджиСкачать

Конверсионные стратегии для специалистов: как их настроить и эффективно использоватьСкачать

Когда тренер - твой друг😏Скачать

Шалимов и Панов: как может продавать креативСкачать