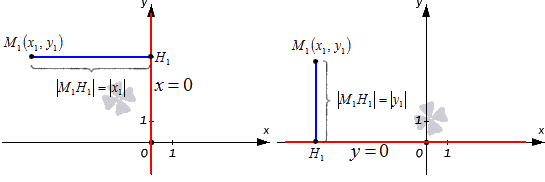С помощю этого онлайн калькулятора можно найти расстояние от точки до прямой. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до прямой, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».
- Предупреждение
- Расстояние от точки до прямой − теория, примеры и решения
- 1. Расстояние от точки до прямой на плоскости
- 2. Расстояние от точки до прямой в пространстве
- Расстояние от точки до прямой на плоскости и в пространстве: определение и примеры нахождения
- Расстояние от точки до прямой – определение
- Расстояние от точки до прямой на плоскости – теория, примеры, решения
- Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости
- Расстояние от точки до прямой в пространстве – теория, примеры, решения
- Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве
- Расстояние от точки до прямой на плоскости.
- Формула для вычисления расстояния от точки до прямой на плоскости
- Примеры задач на вычисление расстояния от точки до прямой на плоскости
- Решение задач по математике онлайн
- Калькулятор онлайн. Вычисление расстояния от точки до прямой
- 💡 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:18. Расстояние от точки до прямой в пространствеСкачать

Расстояние от точки до прямой − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
1. Расстояние от точки до прямой на плоскости
Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
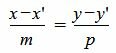 , , | (1) |
где q=(m,p) направляющий вектор прямой L.
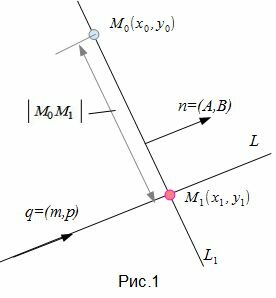
Найдем расстояние от точки M0 до прямой (1)(Рис.1).
 |
Алгоритм нахождения расстояния от точки M0 до прямой L содержит следующие шаги:
- построить прямую L1, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение прямых L и L1(точка M1)
- найти найти расстояние между точками M0 и M1.
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
| A(x−x0)+B(y−y0)=0 | (2) |
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
| m(x−x0)+p(y−y0)=0 | (3) |
| mx+py−mx0−py0=0 | (4) |
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
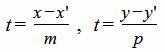 |
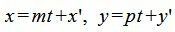 | (5) |
Подставим значения x и y в (4):
| m(mt+x’)+p(pt+y’)−mx0−py0=0 |
| m 2 t+mx’+p 2 t+py’−mx0−py0=0 |
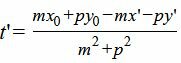 | (6) |
Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M0 на прямую L:
Далее находим расстояние между точками M0 и M1 используя формулу:
 . . | (7) |
Пример 1. Найти расстояние от точки M0(−6, 2) до прямой
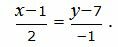 | (8) |
Направляющий вектор прямой (8) имеет вид:
Т.е. m=2, p=−1. Из уравнения прямой (8) видно, что она проходит через точку M’ (x’, y’)=(1, 7)(в этом легко убедится − подставляя эти значения в (8) получим тождество 0=0), т.е. x’=1, y’=7. Подставим значения m, p, x0, y0, x’, y’ в (6):
 |
 |
 , , |
Подставляя значение t в (5), получим:
 |
Вычислим расстояние между точками M0(-6, 2) и M1
 |
Упростим и решим:
  |
Расстояние от точки M0(-6, 2) до прямой (8) :
 |
2. Расстояние от точки до прямой в пространстве
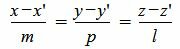 , , | (9) |
где q=(m, p, l) направляющий вектор прямой L.
Найдем расстояние от точки M0 до прямой (9)(Рис.2).
 |
Алгоритм нахождения расстояния от точки до прямой L содержит следующие шаги:
- построить плоскость α, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение плоскости α и прямой L(точка M1)
- найти расстояние между точками M0 и M1.
| A(x−x0)+B(y−y0)+C(z−z0)=0 | (10) |
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (10) можно записать так:
| m(x−x0)+p(y−y0)+l(z−z0)=0 |
| mx+py+lz−mx0−py0−lz0=0 | (11) |
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (9):
 |
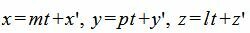 | (12) |
Подставим значения x и y в (11):
| m(mt+x’)+p(pt+y’)+l(lt+z’)−mx0−py0−lz0=0 |
| m 2 t+mx’+p 2 t+py’+l 2 t+ly’−mx0−py0−lz0=0 |
 | (13) |
Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (11). Следовательно, подставляя значение t’ в (12) получим координаты проекции точки M0 на прямую L:
| M1(x1, y1, , z1), |
Далее вычисляем расстояние между точками M0 и M1 используя формулу
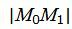 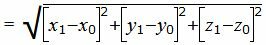 , , | (14) |
которое является расстоянием между точкой M0 и прямой (9).
Пример 2. Найти расстояние от точки M0(1, 2, 1) до прямой
 | (15) |
Направляющий вектор прямой (15) имеет вид:
Т.е. m=2, p=4, l=−6. Из уравнения прямой (15) видно, что она проходит через точку M’ (x’, y’, z’)=(4, 3, 1)(в этом легко убедится − подставляя эти значения в (15) получим тождество 0=0=0), т.е. x’=4, y’=3, z’=1. Подставим значения m, p, l x0, y0, z0 x’, y’, z’ в (13):
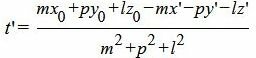 |
 |
 |
Подставляя значение t=t’ в (12), получим координаты точки M1:
 , , |
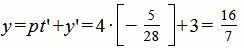 , , |
 . . |
Далее, используя формулу (14) вычисляем расстояние от точки M0 до прямой (15):
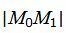 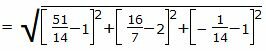 . . |
Упростим и решим:
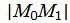   . . |
Расстояние от точки M0(1, 2, 1) до прямой (15) :
Видео:Расстояние от точки до прямой (метод координат)Скачать

Расстояние от точки до прямой на плоскости и в пространстве: определение и примеры нахождения
Данная статья рассказывает о теме «расстояния от точки до прямой», рассматриваются определения расстояния от точки к прямой с иллюстрированными примерами методом координат. Каждый блок теории в конце имеет показанные примеры решения подобных задач.
Видео:Расстояние от точки до прямойСкачать

Расстояние от точки до прямой – определение
Расстояние от точки до прямой находится через определение расстояния от точки до точки. Рассмотрим подробней.
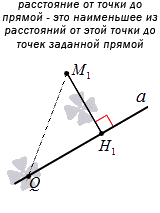
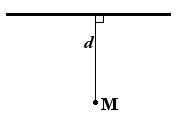
Пусть имеется прямая a и точка М 1 , не принадлежащая заданной прямой. Через нее проведем прямую b , расположенную перпендикулярно относительно прямой a . Точка пересечения прямых возьмем за Н 1 . Получим, что М 1 Н 1 является перпендикуляром, который опустили из точки М 1 к прямой a .
Расстоянием от точки М 1 к прямой a называется расстояние между точками М 1 и Н 1 .
Бывают записи определения с фигурированием длины перпендикуляра.
Расстоянием от точки до прямой называют длину перпендикуляра, проведенного из данной точки к данной прямой.
Определения эквивалентны. Рассмотрим рисунок, приведенный ниже.
Известно, что расстояние от точки до прямой является наименьшим из всех возможных. Рассмотрим это на примере.
Если взять точку Q , лежащую на прямой a , не совпадающую с точкой М 1 , тогда получим, что отрезок М 1 Q называется наклонной, опущенной из М 1 к прямой a . Необходимо обозначить, что перпендикуляр из точки М 1 является меньше, чем любая другая наклонная, проведенная из точки к прямой.
Чтобы доказать это, рассмотрим треугольник М 1 Q 1 Н 1 , где М 1 Q 1 является гипотенузой. Известно, что ее длина всегда больше длины любого из катетов. Значим, имеем, что M 1 H 1 M 1 Q . Рассмотрим рисунок, приведенный ниже.
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Расстояние от точки до прямой на плоскости – теория, примеры, решения
Исходные данные для нахождения от точки до прямой позволяют использовать несколько методов решения: через теорему Пифагора, определения синуса, косинуса, тангенса угла и другими. Большинство заданий такого типа решают в школе на уроках геометрии.
Когда при нахождении расстояния от точки до прямой можно ввести прямоугольную систему координат, то применяют метод координат. В данном пункте рассмотрим основных два метода нахождения искомого расстояния от заданной точки.
Первый способ подразумевает поиск расстояния как перпендикуляра, проведенного из М 1 к прямой a . Во втором способе используется нормальное уравнение прямой а для нахождения искомого расстояния.
Если на плоскости имеется точка с координатами M 1 ( x 1 , y 1 ) , расположенная в прямоугольной системе координат, прямая a , а необходимо найти расстояние M 1 H 1 , можно произвести вычисление двумя способами. Рассмотрим их.
Если имеются координаты точки H 1 , равные x 2 , y 2 , тогда расстояние от точки до прямой вычисляется по координатам из формулы M 1 H 1 = ( x 2 — x 1 ) 2 + ( y 2 — y 1 ) 2 .
Теперь перейдем к нахождению координат точки Н 1 .
Известно, что прямая линия в О х у соответствует уравнению прямой на плоскости. Возьмем способ задания прямой a через написание общего уравнения прямой или уравнения с угловым коэффициентом. Составляем уравнение прямой, которая проходит через точку М 1 перпендикулярно заданной прямой a . Прямую обозначим буковой b . Н 1 является точкой пересечения прямых a и b , значит для определения координат необходимо воспользоваться статьей, в которой идет речь о координатах точек пересечения двух прямых.
Видно, что алгоритм нахождения расстояния от заданной точки M 1 ( x 1 , y 1 ) до прямой a проводится согласно пунктам:
- нахождение общего уравнения прямой a , имеющее вид A 1 x + B 1 y + C 1 = 0 ,или уравнение с угловым коэффициентом, имеющее вид y = k 1 x + b 1 ;
- получение общего уравнения прямой b , имеющее вид A 2 x + B 2 y + C 2 = 0 или уравнение с угловым коэффициентом y = k 2 x + b 2 , если прямая b пересекает точку М 1 и является перпендикулярной к заданной прямой a ;
- определение координат x 2 , y 2 точки Н 1 , являющейся точкой пересечения a и b , для этого производится решение системы линейных уравнений A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 или y = k 1 x + b 1 y = k 2 x + b 2 ;
- вычисление искомого расстояния от точки до прямой, используя формулу M 1 H 1 = ( x 2 — x 1 ) 2 + ( y 2 — y 1 ) 2 .
Теорема способна помочь ответить на вопрос о нахождении расстояния от заданной точки до заданной прямой на плоскости.
Прямоугольная система координат имеет О х у имеет точку M 1 ( x 1 , y 1 ) , из которой проведена прямая а к плоскости, задаваемая нормальным уравнением плоскости, имеющее вид cos α · x + cos β · y — p = 0 , равно по модулю значению, получаемому в левой части нормального уравнения прямой, вычисляемому при x = x 1 , y = y 1 , значит, что M 1 H 1 = cos α · x 1 + cos β · y 1 — p .
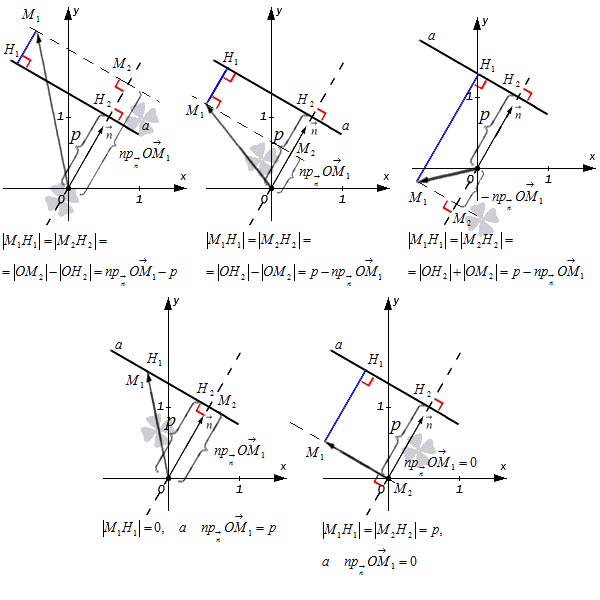
Прямой а соответствует нормальное уравнение плоскости, имеющее вид cos α · x + cos β · y — p = 0 , тогда n → = ( cos α , cos β ) считается нормальным вектором прямой a при расстоянии от начала координат до прямой a с p единицами. Необходимо изобразить все данные на рисунке, добавить точку с координатами M 1 ( x 1 , y 1 ) , где радиус-вектор точки М 1 — O M 1 → = ( x 1 , y 1 ) . Необходимо провести прямую от точки до прямой, которое обозначим M 1 H 1 . Необходимо показать проекции М 2 и Н 2 точек М 1 и Н 2 на прямую, проходящую через точку O с направляющим вектором вида n → = ( cos α , cos β ) , а числовую проекцию вектора обозначим как O M 1 → = ( x 1 , y 1 ) к направлению n → = ( cos α , cos β ) как n p n → O M 1 → .
Вариации зависят от расположения самой точки М 1 . Рассмотрим на рисунке, приведенном ниже.
Результаты фиксируем при помощи формулы M 1 H 1 = n p n → O M → 1 — p . После чего приводим равенство к такому виду M 1 H 1 = cos α · x 1 + cos β · y 1 — p для того, чтобы получить n p n → O M → 1 = cos α · x 1 + cos β · y 1 .
Скалярное произведение векторов в результате дает преобразованную формулу вида n → , O M → 1 = n → · n p n → O M 1 → = 1 · n p n → O M 1 → = n p n → O M 1 → , которая является произведением в координатной форме вида n → , O M 1 → = cos α · x 1 + cos β · y 1 . Значит, получаем, что n p n → O M 1 → = cos α · x 1 + cos β · y 1 . Отсюда следует, что M 1 H 1 = n p n → O M 1 → — p = cos α · x 1 + cos β · y 1 — p . Теорема доказана.
Получаем, что для нахождения расстояния от точки M 1 ( x 1 , y 1 ) к прямой a на плоскости необходимо выполнить несколько действий:
- получение нормального уравнения прямой a cos α · x + cos β · y — p = 0 , при условии, что его нет в задании;
- вычисление выражения cos α · x 1 + cos β · y 1 — p , где полученное значение принимает M 1 H 1 .
Видео:Лекция 48. Как найти расстояние между прямой и началом координат?Скачать

Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости
Применим данные методы на решении задач с нахождением расстояния от точки до плоскости.
Найти расстояние от точки с координатами M 1 ( — 1 , 2 ) к прямой 4 x — 3 y + 35 = 0 .
Применим первый способ для решения.
Для этого необходимо найти общее уравнение прямой b , которая проходит через заданную точку M 1 ( — 1 , 2 ) , перпендикулярно прямой 4 x — 3 y + 35 = 0 . Из условия видно, что прямая b является перпендикулярной прямой a , тогда ее направляющий вектор имеет координаты, равные ( 4 , — 3 ) . Таким образом имеем возможность записать каноническое уравнение прямой b на плоскости, так как имеются координаты точки М 1 , принадлежит прямой b . Определим координаты направляющего вектора прямой b . Получим, что x — ( — 1 ) 4 = y — 2 — 3 ⇔ x + 1 4 = y — 2 — 3 . Полученное каноническое уравнение необходимо преобразовать к общему. Тогда получаем, что
x + 1 4 = y — 2 — 3 ⇔ — 3 · ( x + 1 ) = 4 · ( y — 2 ) ⇔ 3 x + 4 y — 5 = 0
Произведем нахождение координат точек пересечения прямых, которое примем за обозначение Н 1 . Преобразования выглядят таким образом:
4 x — 3 y + 35 = 0 3 x + 4 y — 5 = 0 ⇔ x = 3 4 y — 35 4 3 x + 4 y — 5 = 0 ⇔ x = 3 4 y — 35 4 3 · 3 4 y — 35 4 + 4 y — 5 = 0 ⇔ ⇔ x = 3 4 y — 35 4 y = 5 ⇔ x = 3 4 · 5 — 35 4 y = 5 ⇔ x = — 5 y = 5
Из выше написанного имеем, что координаты точки Н 1 равны ( — 5 ; 5 ) .
Необходимо вычислить расстояние от точки М 1 к прямой a . Имеем, что координаты точек M 1 ( — 1 , 2 ) и H 1 ( — 5 , 5 ) , тогда подставляем в формулу для нахождения расстояния и получаем, что
M 1 H 1 = ( — 5 — ( — 1 ) 2 + ( 5 — 2 ) 2 = 25 = 5
Второй способ решения.
Для того, чтобы решить другим способом, необходимо получить нормальное уравнение прямой. Вычисляем значение нормирующего множителя и умножаем обе части уравнения 4 x — 3 y + 35 = 0 . Отсюда получим, что нормирующий множитель равен — 1 4 2 + ( — 3 ) 2 = — 1 5 , а нормальное уравнение будет вида — 1 5 · 4 x — 3 y + 35 = — 1 5 · 0 ⇔ — 4 5 x + 3 5 y — 7 = 0 .
По алгоритму вычисления необходимо получить нормальное уравнение прямой и вычислить его со значениями x = — 1 , y = 2 . Тогда получаем, что
— 4 5 · — 1 + 3 5 · 2 — 7 = — 5
Отсюда получаем, что расстояние от точки M 1 ( — 1 , 2 ) к заданной прямой 4 x — 3 y + 35 = 0 имеет значение — 5 = 5 .
Видно, что в данном методе важно использование нормального уравнения прямой, так как такой способ является наиболее коротким. Но первый метод удобен тем, что последователен и логичен, хотя имеет больше пунктов вычисления.
На плоскости имеется прямоугольная система координат О х у с точкой M 1 ( 8 , 0 ) и прямой y = 1 2 x + 1 . Найти расстояние от заданной точки до прямой.
Решение первым способом подразумевает приведение заданного уравнения с угловым коэффициентом к уравнению общего вида. Для упрощения можно сделать иначе.
Если произведение угловых коэффициентов перпендикулярных прямых имеют значение — 1 , значит угловой коэффициент прямой перпендикулярной заданной y = 1 2 x + 1 имеет значение 2 . Теперь получим уравнение прямой, проходящее через точку с координатами M 1 ( 8 , 0 ) . Имеем, что y — 0 = — 2 · ( x — 8 ) ⇔ y = — 2 x + 16 .
Переходим к нахождению координат точки Н 1 , то есть точкам пересечения y = — 2 x + 16 и y = 1 2 x + 1 . Составляем систему уравнений и получаем:
y = 1 2 x + 1 y = — 2 x + 16 ⇔ y = 1 2 x + 1 1 2 x + 1 = — 2 x + 16 ⇔ y = 1 2 x + 1 x = 6 ⇔ ⇔ y = 1 2 · 6 + 1 x = 6 = y = 4 x = 6 ⇒ H 1 ( 6 , 4 )
Отсюда следует, что расстояние от точки с координатами M 1 ( 8 , 0 ) к прямой y = 1 2 x + 1 равно расстоянию от точки начала и точки конца с координатами M 1 ( 8 , 0 ) и H 1 ( 6 , 4 ) . Вычислим и получим, что M 1 H 1 = 6 — 8 2 + ( 4 — 0 ) 2 20 = 2 5 .
Решение вторым способом заключается в переходе от уравнения с коэффициентом к нормальному его виду. То есть получим y = 1 2 x + 1 ⇔ 1 2 x — y + 1 = 0 , тогда значение нормирующего множителя будет — 1 1 2 2 + ( — 1 ) 2 = — 2 5 . Отсюда следует, что нормальное уравнение прямой принимает вид — 2 5 · 1 2 x — y + 1 = — 2 5 · 0 ⇔ — 1 5 x + 2 5 y — 2 5 = 0 . Произведем вычисление от точки M 1 8 , 0 к прямой вида — 1 5 x + 2 5 y — 2 5 = 0 . Получаем:
M 1 H 1 = — 1 5 · 8 + 2 5 · 0 — 2 5 = — 10 5 = 2 5
Необходимо вычислить расстояние от точки с координатами M 1 ( — 2 , 4 ) к прямым 2 x — 3 = 0 и y + 1 = 0 .
Получаем уравнение нормального вида прямой 2 x — 3 = 0 :
2 x — 3 = 0 ⇔ 1 2 · 2 x — 3 = 1 2 · 0 ⇔ x — 3 2 = 0
После чего переходим к вычислению расстояния от точки M 1 — 2 , 4 к прямой x — 3 2 = 0 . Получаем:
M 1 H 1 = — 2 — 3 2 = 3 1 2
Уравнение прямой y + 1 = 0 имеет нормирующий множитель со значением равным -1. Это означает, что уравнение примет вид — y — 1 = 0 . Переходим к вычислению расстояния от точки M 1 ( — 2 , 4 ) к прямой — y — 1 = 0 . Получим, что оно равняется — 4 — 1 = 5 .
Ответ: 3 1 2 и 5 .
Подробно рассмотрим нахождение расстояния от заданной точки плоскости к координатным осям О х и О у .
В прямоугольной системе координат у оси О у имеется уравнение прямой, которое является неполным имеет вида х = 0 , а О х — y = 0 . Уравнения являются нормальными для осей координат, тогда необходимо найти расстояние от точки с координатами M 1 x 1 , y 1 до прямых. Это производится, исходя из формул M 1 H 1 = x 1 и M 1 H 1 = y 1 . Рассмотрим на рисунке, приведенном ниже.
Найти расстояние от точки M 1 ( 6 , — 7 ) до координатных прямых, расположенных в плоскости О х у .
Так как уравнение у = 0 относится к прямой О х , можно найти расстояние от M 1 с заданными координатами, до этой прямой, используя формулу. Получаем, что 6 = 6 .
Так как уравнение х = 0 относится к прямой О у , то можно найти расстояние от М 1 к этой прямой по формуле. Тогда получим, что — 7 = 7 .
Ответ: расстояние от М 1 к О х имеет значение 6 , а от М 1 к О у имеет значение 7 .
Видео:Расстояние от точки до плоскости / Вывод формулыСкачать

Расстояние от точки до прямой в пространстве – теория, примеры, решения
Когда в трехмерном пространстве имеем точку с координатами M 1 ( x 1 , y 1 , z 1 ) , необходимо найти расстояние от точки A до прямой a .
Рассмотрим два способа, которые позволяют производить вычисление расстояние от точки до прямой a , расположенной в пространстве. Первый случай рассматривает расстояние от точки М 1 к прямой, где точка на прямой называется Н 1 и является основанием перпендикуляра, проведенного из точки М 1 на прямую a . Второй случай говорит о том, что точки этой плоскости необходимо искать в качестве высоты параллелограмма.
Из определения имеем, что расстояние от точки М 1 , расположенной на прямой а, является длиной перпендикуляра М 1 Н 1 , тогда получим, что при найденных координатах точки Н 1 , тогда найдем расстояние между M 1 ( x 1 , y 1 , z 1 ) и H 1 ( x 1 , y 1 , z 1 ) , исходя из формулы M 1 H 1 = x 2 — x 1 2 + y 2 — y 1 2 + z 2 — z 1 2 .
Получаем, что все решение идет к тому, чтобы найти координаты основания перпендикуляра, проведенного из М 1 на прямую a . Это производится следующим образом: Н 1 является точкой, где пересекаются прямая a с плоскостью, которая проходит через заданную точку.
Значит, алгоритм определения расстояния от точки M 1 ( x 1 , y 1 , z 1 ) к прямой a пространства подразумевает несколько пунктов:
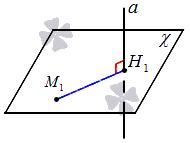
- составление уравнение плоскости χ в качестве уравнения плоскости, проходящего через заданную точку, находящуюся перпендикулярно прямой;
- определение координат ( x 2 , y 2 , z 2 ) , принадлежавших точке Н 1 , которая является точкой пересечения прямой a и плоскости χ ;
- вычисление расстояния от точки до прямой при помощи формулы M 1 H 1 = x 2 — x 1 2 + y 2 — y 1 2 + z 2 — z 1 2 .
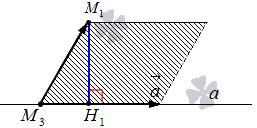
Из условия имеем прямую a , тогда можем определить направляющий вектор a → = a x , a y , a z с координатами x 3 , y 3 , z 3 и определенной точки М 3 ,принадлежащей прямой a . При наличии координат точек M 1 ( x 1 , y 1 ) и M 3 x 3 , y 3 , z 3 можно произвести вычисление M 3 M 1 → :
M 3 M 1 → = ( x 1 — x 3 , y 1 — y 3 , z 1 — z 3 )
Следует отложить векторы a → = a x , a y , a z и M 3 M 1 → = x 1 — x 3 , y 1 — y 3 , z 1 — z 3 из точки М 3 , соединим и получим фигуру параллелограмма. М 1 Н 1 является высотой параллелограмма.
Рассмотрим на рисунке, приведенном ниже.
Имеем, что высота М 1 Н 1 является искомым расстоянием, тогда необходимо найти его по формуле. То есть ищем M 1 H 1 .
Обозначим площадь параллелограмма за букву S , находится по формуле, используя вектор a → = ( a x , a y , a z ) и M 3 M 1 → = x 1 — x 3 . y 1 — y 3 , z 1 — z 3 . Формула площади имеет вид S = a → × M 3 M 1 → . Также площадь фигуры равняется произведению длин его сторон на высоту, получим, что S = a → · M 1 H 1 с a → = a x 2 + a y 2 + a z 2 , являющимся длиной вектора a → = ( a x , a y , a z ) , являющейся равной стороне параллелограмма. Значит, M 1 H 1 является расстоянием от точки до прямой. Ее нахождение производится по формуле M 1 H 1 = a → × M 3 M 1 → a → .
Для нахождения расстояния от точки с координатами M 1 ( x 1 , y 1 , z 1 ) до прямой a в пространстве, необходимо выполнить несколько пунктов алгоритма:
- определение направляющего вектора прямой a — a → = ( a x , a y , a z ) ;
- вычисление длины направляющего вектора a → = a x 2 + a y 2 + a z 2 ;
- получение координат x 3 , y 3 , z 3 , принадлежавших точке М3, находящейся на прямой а;
- вычисление координат вектора M 3 M 1 → ;
- нахождение векторного произведения векторов a → ( a x , a y , a z ) и M 3 M 1 → = x 1 — x 3 , y 1 — y 3 , z 1 — z 3 в качестве a → × M 3 M 1 → = i → j → k → a x a y a z x 1 — x 3 y 1 — y 3 z 1 — z 3 для получения длины по формуле a → × M 3 M 1 → ;
- вычисление расстояния от точки до прямой M 1 H 1 = a → × M 3 M 1 → a → .
Видео:Видеоурок "Расстояние от точки до прямой"Скачать

Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве
Найти расстояние от точки с координатами M 1 2 , — 4 , — 1 к прямой x + 1 2 = y — 1 = z + 5 5 .
Первый способ начинается с записи уравнения плоскости χ , проходящей через М 1 и перпендикулярно заданной точке. Получаем выражение вида:
2 · ( x — 2 ) — 1 · ( y — ( — 4 ) ) + 5 · ( z — ( — 1 ) ) = 0 ⇔ 2 x — y + 5 z — 3 = 0
Нужно найти координаты точки H 1 , являющейся точкой пересечения с плоскостью χ к заданной по условию прямой. Следует переходить от канонического вида к пересекающемуся. Тогда получаем систему уравнений вида:
x + 1 2 = y — 1 = z + 5 5 ⇔ — 1 · ( x + 1 ) = 2 · y 5 · ( x + 1 ) = 2 · ( z + 5 ) 5 · y = — 1 · ( z + 5 ) ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0
Необходимо вычислить систему x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 2 x — y + 5 z — 3 = 0 ⇔ x + 2 y = — 1 5 x — 2 z = 5 2 x — y + 5 z = 3 по методу Крамера, тогда получаем, что:
∆ = 1 2 0 5 0 — 2 2 — 1 5 = — 60 ∆ x = — 1 2 0 5 0 — 2 3 — 1 5 = — 60 ⇔ x = ∆ x ∆ = — 60 — 60 = 1 ∆ y = 1 — 1 0 5 5 2 2 3 5 = 60 ⇒ y = ∆ y ∆ = 60 — 60 = — 1 ∆ z = 1 2 — 1 5 0 5 2 — 1 3 = 0 ⇒ z = ∆ z ∆ = 0 — 60 = 0
Отсюда имеем, что H 1 ( 1 , — 1 , 0 ) .
Необходимо рассчитать расстояние между точками с координатами M 1 ( 2 , — 4 , — 1 ) и H 1 ( 1 , — 1 , 0 ) по формуле:
M 1 H 1 = 1 — 2 2 + — 1 — — 4 2 + 0 — — 1 2 = 11
Второй способ необходимо начать с поиска координат в каноническом уравнении. Для этого необходимо обратит внимание на знаменатели дроби. Тогда a → = 2 , — 1 , 5 является направляющим вектором прямой x + 1 2 = y — 1 = z + 5 5 . Необходимо вычислить длину по формуле a → = 2 2 + ( — 1 ) 2 + 5 2 = 30 .
Понятно, что прямая x + 1 2 = y — 1 = z + 5 5 пересекает точку M 3 ( — 1 , 0 , — 5 ) , отсюда имеем, что вектор с началом координат M 3 ( — 1 , 0 , — 5 ) и его концом в точке M 1 2 , — 4 , — 1 является M 3 M 1 → = 3 , — 4 , 4 . Находим векторное произведение a → = ( 2 , — 1 , 5 ) и M 3 M 1 → = ( 3 , — 4 , 4 ) .
Мы получаем выражение вида a → × M 3 M 1 → = i → j → k → 2 — 1 5 3 — 4 4 = — 4 · i → + 15 · j → — 8 · k → + 20 · i → — 8 · j → = 16 · i → + 7 · j → — 5 · k →
получаем, что длина векторного произведения равняется a → × M 3 M 1 → = 16 2 + 7 2 + — 5 2 = 330 .
Имеются все данные для использования формулы вычисления расстояния от точки для прямлой, поэтому применим ее и получим:
M 1 H 1 = a → × M 3 M 1 → a → = 330 30 = 11
Видео:7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Расстояние от точки до прямой на плоскости.
Видео:Определить расстояние от точки С до прямой АВ. Метод прямоугольного треугольника.Скачать

Формула для вычисления расстояния от точки до прямой на плоскости
Если задано уравнение прямой A x + B y + C = 0, то расстояние от точки M(M x , M y ) до прямой можно найти, используя следующую формулу
| d = | |A·M x + B·M y + C| |
| √ A 2 + B 2 |
Видео:Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать

Примеры задач на вычисление расстояния от точки до прямой на плоскости
Решение. Подставим в формулу коэффициенты прямой и координаты точки
| d = | |3·(-1) + 4·3 — 6| | = | |-3 + 12 — 6| | = | |3| | = 0.6 |
| √ 3 2 + 4 2 | √ 9 + 16 | 5 |
Ответ: расстояние от точки до прямой равно 0.6.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Видеоурок "Нормальное уравнение прямой"Скачать

Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:Лекция 24. Расстояние от точки до прямой на плоскости.Скачать

Калькулятор онлайн.
Вычисление расстояния от точки до прямой
Этот калькулятор онлайн вычисляет расстояние от точки до прямой заданной в каноническом виде (для трехмерного случая):
Онлайн калькулятор для вычисления расстояния от точки до прямой не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac )
💡 Видео
§15 Расстояние от точки до прямойСкачать

7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Расстояние от точки до прямой | Вывод формулы через Подобие и ПифагораСкачать

Расстояние от точки до прямой на координатной плоскости как найти, примерСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Видеоурок "Расстояние от точки до прямой"Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Метод координат . Урок № 7. Нахождение расстояния от точки до прямой.Скачать