Теорема 6. Пусть на [a,b] задана дважды дифференцируемая функция f(x), причем выполнены след. условия
а) f(a)f(b) 0
можно вычислить модифицированным методом Ньютона единственный корень ξ с любой степенью точности.
Доказательство: Пусть f’(x)>0, f’’(x0)>0 (см.рис.3) Тогда в качестве x0 берем точку x0=b, так как f(b)f’’(b)>0. Из (3.23) следует, что xn+1 x1>…>xn>a (3.24)
Покажем теперь, что эта последовательность имеет предел ξ. Пусть xn-1> ξ. Докажем, что xn> ξ. Для этого запишем n-ое приближение, полученное по формуле Ньютона (см. формулу (3.17)) и по модифицированной формуле Ньютона (3.23)
и найдем разность . (3.25)
Из теории выпуклых функций известно, что если f’’(x) и сохраняет знак на [a,b], то f(x)является выпуклой. Для выпуклой функции f(x) производная f’(x) является неубывающей, то есть для . Поэтому . (3.26)
С учетом (3.26) из (11) следует . Из теоремы 5 сходимости метода Ньютона мы получали , поэтому . Отсюда
ξ≤xn. (3.27)
Таким образом, из (3.24) и (3.27) получили убывающую сходящуюся последовательность
x0>x1>…>xn≥ξ.
Следовательно, для любого сколь угодно малого ε>0 можно указать такое n, что
|xn-ξ|
Видео:МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать
Модификации метода ньютона для систем нелинейных уравнений
нПДЙЖЙЛБГЙЙ НЕФПДБ оШАФПОБ.
нЕФПД УЕЛХЭЙИ ДМС ОЕМЙОЕКОПЗП ХТБЧОЕОЙС.
НЕФПДБ оШАФПОБ ФТЕВХЕФУС ЧЩЮЙУМСФШ РТПЙЪЧПДОХА ЖХОЛГЙЙ f(x), ЮФП ОЕ ЧУЕЗДБ ХДПВОП, Б ЙОПЗДБ РТБЛФЙЮЕУЛЙ ОЕЧПЪНПЦОП. ч НЕФПДЕ УЕЛХЭЙИ РТПЙЪЧПДОБС f ‘(x (k) ) ЪБНЕОСЕФУС ОБ ДТПВШ (ФБЛ ОБЪЩЧБЕНХА ТБЪДЕМЕООХА ТБЪОПУФШ) (f(x (k) ) — f(x (k-1) )) / (x (k) — x (k-1) ).
ч ТЕЪХМШФБФЕ ЖПТНХМБ НЕФПДБ РТЙОЙНБЕФ ЧЙД:
| x (k+1) = x (k) — f(x (k) )(x (k) — x (k-1) ) / (f(x (k) ) — f(x (k-1) )), k = 1, 2, . | (2.19) |
|---|
ЗДЕ x (0) ,x (1) — ОЕЛПФПТЩЕ ОБЮБМШОЩЕ РТЙВМЙЦЕОЙС Л ЛПТОА.
зЕПНЕФТЙЮЕУЛЙК УНЩУМ НЕФПДБ УЕЛХЭЙИ ЪБЛМАЮБЕФУС Ч ЪБНЕОЕ ОБ ЙФЕТБГЙЙ У ОПНЕТПН k ЗТБЖЙЛБ ЖХОЛГЙЙ y=f(И) ОБ УЕЛХЭХА, РТПИПДСЭХА ЮЕТЕЪ ФПЮЛЙ (x (k) ,f(x (k) )) Й (x (k-1) ,f(x (k-1) )) Й, УМЕДПЧБФЕМШОП, ЪБДБЧБЕНХА ХТБЧОЕОЙЕН
дБМЕЕ ОБИПДЙН ФПЮЛХ ЕЕ РЕТЕУЕЮЕОЙС У ПУША OX, ЮФП УППФЧЕФУФЧХЕФ ТЕЫЕОЙА МЙОЕКОПЗП ХТБЧОЕОЙС:
1) ч ПВЭЕН УМХЮБЕ УИПДЙНПУФШ РП НЕФПДХ оШАФПОБ РТПЙУИПДЙФ ВЩУФТЕЕ, ЮЕН РП НЕФПДХ УЕЛХЭЙИ, Й ЛТПНЕ ФПЗП ОЕ ФТЕВХЕФУС ОБИПЦДЕОЙС УТБЪХ ДЧХИ ОБЮБМШОЩИ РТЙВМЙЦЕОЙК Л ЙУЛПНПНХ ЛПТОА. оП РТЙ ЙУРПМШЪПЧБОЙЙ НЕФПДБ УЕЛХЭЙИ ОЕ ФТЕВХЕФУС ЧЩЮЙУМЕОЙС РТПЙЪЧПДОПК.
2) хУМПЧЙЕ ПЛПОЮБОЙС ЙФЕТБГЙК Ч НЕФПДЕ УЕЛХЭЙИ ПУФБЕФУС ФЕН ЦЕ, ЮФП Й Ч ЛМБУУЙЮЕУЛПН НЕФПДЕ оШАФПОБ: | x (k+1) — x (k) | ≤ ε.
нЕФПД ИПТД ДМС ОЕМЙОЕКОПЗП ХТБЧОЕОЙС.
ч НЕФПДЕ ИПТД РТПЙЪЧПДОБС f ‘(x (k) ) НЕФПДБ оШАФПОБ ЪБНЕОСЕФУС ОБ ЕЭЕ ВПМЕЕ РТПУФХА (РП УТБЧОЕОЙА У НЕФПДПН УЕЛХЭЙИ) ТБЪДЕМЕООХА ТБЪОПУФШ (f(x (k) ) — f(x (0) )) / (x (k) — x (0) )
ч ТЕЪХМШФБФЕ ЖПТНХМБ НЕФПДБ ИПТД РТЙОЙНБЕФ ЧЙД:
| x (k+1) = x (k) — f(x (k) )(x (k) — x (0) ) / (f(x (k) ) — f(x (0) )), k = 1, 2, . | (2.20) |
|---|
РТЙЮЕН x (0) , x (1) — ОЕЛПФПТЩЕ ОБЮБМШОЩЕ РТЙВМЙЦЕОЙС Л ЛПТОА. зЕПНЕФТЙЮЕУЛЙ ТБУУНБФТЙЧБЕНЩК НЕФПД ПЪОБЮБЕФ ЪБНЕОХ ОБ ЛБЦДПК ЙФЕТБГЙЙ ЗТБЖЙЛБ ЖХОЛГЙЙ y=f(И) ОБ ИПТДХ, ФП ЕУФШ ЮЕТЕЪ ФПЮЛЙ (x (0) ,f(x (0) )) Й (x (k) ,f(x (k) )) РТПЧПДЙН ИПТДХ
Й ОБИПДЙН ФПЮЛХ ЕЕ РЕТЕУЕЮЕОЙС У ПУША OX, ЮФП УППФЧЕФУФЧХЕФ ТЕЫЕОЙА МЙОЕКОПЗП ХТБЧОЕОЙС:
чЩТБЦБС ПФУАДБ x, РПМХЮБЕН:
ъбнеюбойе 2.6 лТЙФЕТЙК ПЛПОЮБОЙС ЙФЕТБГЙК Ч НЕФПДЕ ИПТД ЙНЕЕФ ЧЙД:
хРТПЭЕООЩК НЕФПД оШАФПОБ.
ьФПФ НЕФПД ЙНЕЕФ ЧЙД
| x (k+1) = x (k) — f(x (k) )/f ‘(x (0) ) , k = 0, 1, 2, . | (2.21) |
|---|
ЗДЕ x (0) — ОЕЛПФПТПЕ ОБЮБМШОПЕ РТЙВМЙЦЕОЙЕ Л ЛПТОА.
лТЙФЕТЙК ПЛПОЮБОЙС ДБООПЗП ЙФЕТБГЙПООПЗП РТПГЕУУБ ЙНЕЕФ ЧЙД:
л ДПУФПЙОУФЧБН ЬФПЗП НЕФПДБ УМЕДХЕФ ПФОЕУФЙ РТПУФПФХ ЕЗП ТЕБМЙЪБГЙЙ Й ЧПЪНПЦОПУФШ ПВПВЭЕОЙС ОБ УЙУФЕНЩ ХТБЧОЕОЙК (УН. УМЕДХАЭЙК РБТБЗТБЖ), Б Л ОЕДПУФБФЛБН — ВПМЕЕ НЕДМЕООХА РП УТБЧОЕОЙА У НЕФПДПН оШАФПОБ УИПДЙНПУФШ.
нПДЙЖЙЛБГЙС НЕФПДБ оШАФПОБ ДМС УЙУФЕНЩ ДЧХИ ХТБЧОЕОЙК.
дМС ТЕЫЕОЙС УЙУФЕНЩ ЙЪ ДЧХИ ХТБЧОЕОЙК
ЙУРПМШЪХЕФУС УМЕДХАЭБС НПДЙЖЙЛБГЙС НЕФПДБ оШАФПОБ:
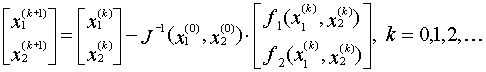 | (2.22) |
|---|
ъбнеюбойе 2.7 1) ч ДБООПН НЕФПДЕ Ч ПФМЙЮЙЕ ПФ ЛМБУУЙЮЕУЛПЗП НЕФПДБ оШАФПОБ ПВТБФОХА НБФТЙГХ ФТЕВХЕФУС РПДУЮЙФЩЧБФШ ФПМШЛП ПДЙО ТБЪ.
2) хУМПЧЙЕ ПЛПОЮБОЙС ЙФЕТБГЙПООПЗП РТПГЕУУБ ЙНЕЕФ ЧЙД: || x (k+1) — x (k) || ≤ ε
Видео:Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать
Нелинейные системы и уравнения
В более общем случае мы имеем не одно уравнение (1), а систему нелинейных уравнений $$ begin tag f_i(x_1, x_2, ldots, x_n) = 0, quad i = 1, 2, ldots n. end $$ Обозначим через ( mathbf = (x_1, x_2, ldots, x_n) ) вектор неизвестных и определим вектор-функцию ( mathbf(mathbf) = (f_1(mathbf), f_2(mathbf), ldots, f_n(mathbf)) ). Тогда система (2) записывается в виде $$ begin tag mathbf(mathbf) = 0. end $$ Частным случаем (3) является уравнение (1) (( n = 1 )). Второй пример (3) — система линейных алгебраических уравнений, когда ( mathbf (mathbf) = A mathbf — mathbf ).
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать
Метод Ньютона
Видео:Методы решения систем нелинейных уравнений. Метод Ньютона. Численные методы. Лекция 14Скачать
Решение нелинейных уравнений
При итерационном решении уравнений (1), (3) задается некоторое начальное приближение, достаточно близкое к искомому решению ( x^* ). В одношаговых итерационных методах новое приближение ( x_ ) определяется по предыдущему приближению ( x_k ). Говорят, что итерационный метод сходится с линейной скоростью, если ( x_ — x^* = O(x_k — x^*) ) и итерационный метод имеет квадратичную сходимость, если ( x_ — x^* = O(x_k — x^*)^2 ).
В итерационном методе Ньютона (методе касательных) для нового приближения имеем $$ begin tag x_ = x_k + frac, quad k = 0, 1, ldots, end $$
Вычисления по (4) проводятся до тех пор, пока ( f(x_k) ) не станет близким к нулю. Более точно, до тех пор, пока ( |f_(x_k)| > varepsilon ), где ( varepsilon ) — малая величина.
Простейшая реализация метода Ньютона может выглядеть следующим образом:
Чтобы найти корень уравнения ( x^2 = 9 ) необходимо реализовать функции
Данная функция хорошо работает для приведенного примера. Однако, в общем случае могут возникать некоторые ошибки, которые нужно отлавливать. Например: пусть нужно решить уравнение ( tanh(x) = 0 ), точное решение которого ( x = 0 ). Если ( |x_0| leq 1.08 ), то метод сходится за шесть итераций.
Теперь зададим ( x_0 ) близким к ( 1.09 ). Возникнет переполнение
Возникнет деление на ноль, так как для ( x_7 = -126055892892.66042 ) значение ( tanh(x_7) ) при машинном округлении равно ( 1.0 ) и поэтому ( f^prime(x_7) = 1 — tanh(x_7)^2 ) становится равной нулю в знаменателе.
Проблема заключается в том, что при таком начальном приближении метод Ньютона расходится.
Еще один недостаток функции naive_Newton заключается в том, что функция f(x) вызывается в два раза больше, чем необходимо.
Учитывая выше сказанное реализуем функцию с учетом следующего:
- обрабатывать деление на ноль
- задавать максимальное число итераций в случае расходимости метода
- убрать лишний вызов функции f(x)
Метод Ньютона сходится быстро, если начальное приближение близко к решению. Выбор начального приближение влияет не только на скорость сходимости, но и на сходимость вообще. Т.е. при неправильном выборе начального приближения метод Ньютона может расходиться. Неплохой стратегией в случае, когда начальное приближение далеко от точного решения, может быть использование нескольких итераций по методу бисекций, а затем использовать метод Ньютона.
При реализации метода Ньютона нужно знать аналитическое выражение для производной ( f^prime(x) ). Python содержит пакет SymPy, который можно использовать для создания функции dfdx . Для нашей задачи это можно реализовать следующим образом:
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать
Решение нелинейных систем
Идея метода Ньютона для приближенного решения системы (2) заключается в следующем: имея некоторое приближение ( pmb^ ), мы находим следующее приближение ( pmb^ ), аппроксимируя ( pmb(pmb^) ) линейным оператором и решая систему линейных алгебраических уравнений. Аппроксимируем нелинейную задачу ( pmb(pmb^) = 0 ) линейной $$ begin tag pmb(pmb^) + pmb(pmb^)(pmb^ — pmb^) = 0, end $$ где ( pmb(pmb^) ) — матрица Якоби (якобиан): $$ pmb(pmb^) = begin frac<partial f_1(pmb^)> & frac<partial f_1(pmb^)> & ldots & frac<partial f_1(pmb^)> \ frac<partial f_2(pmb^)> & frac<partial f_2(pmb^)> & ldots & frac<partial f_2(pmb^)> \ vdots & vdots & ldots & vdots \ frac<partial f_n(pmb^)> & frac<partial f_n(pmb^)> & ldots & frac<partial f_n(pmb^)> \ end $$ Уравнение (5) является линейной системой с матрицей коэффициентов ( pmb ) и вектором правой части ( -pmb(pmb^) ). Систему можно переписать в виде $$ pmb(pmb^)pmb = — pmb(pmb^), $$ где ( pmb = pmb^ — pmb^ ).
Таким образом, ( k )-я итерация метода Ньютона состоит из двух стадий:
1. Решается система линейных уравнений (СЛАУ) ( pmb(pmb^)pmb = -pmb(pmb^) ) относительно ( pmb ).
2. Находится значение вектора на следующей итерации ( pmb^ = pmb^ + pmb ).
Для решения СЛАУ можно использовать приближенные методы. Можно также использовать метод Гаусса. Пакет numpy содержит модуль linalg , основанный на известной библиотеке LAPACK, в которой реализованы методы линейной алгебры. Инструкция x = numpy.linalg.solve(A, b) решает систему ( Ax = b ) методом Гаусса, реализованным в библиотеке LAPACK.
Когда система нелинейных уравнений возникает при решении задач для нелинейных уравнений в частных производных, матрица Якоби часто бывает разреженной. В этом случае целесообразно использовать специальные методы для разреженных матриц или итерационные методы.
Можно также воспользоваться методами, реализованными для систем линейных уравнений.
🔍 Видео
Способы решения систем нелинейных уравнений. 9 класс.Скачать
Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать
4.2 Решение систем нелинейных уравнений. МетодыСкачать
15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать
10 Численные методы решения нелинейных уравненийСкачать
После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать
Метод касательных (метод Ньютона)Скачать
Вычислительная математика. Лекция 4. Решение нелинейных уравнений и систем уравненийСкачать
Метод Зейделя Пример РешенияСкачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Метод Ньютона для решения нелинйеных уравнений в MS ExcelСкачать
10 Метод Ньютона (Метод касательных) C++ Численные методы решения нелинейного уравненияСкачать
Решение системы нелинейных уравнений графическим способом средствами ExcelСкачать
Решение нелинейного уравнения методом Ньютона (касательных) (программа)Скачать
