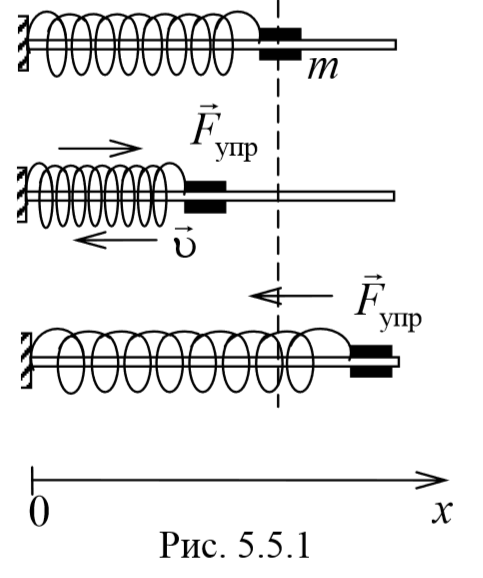
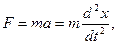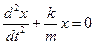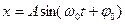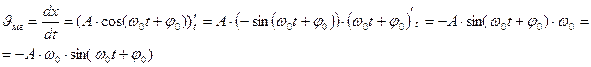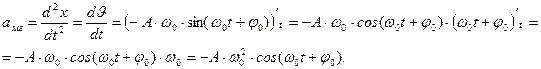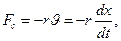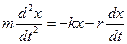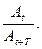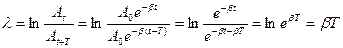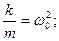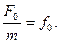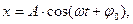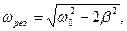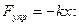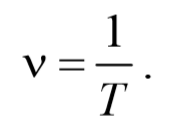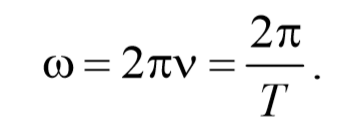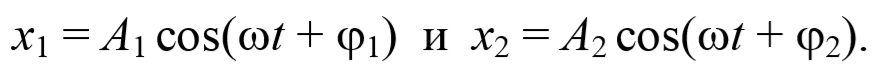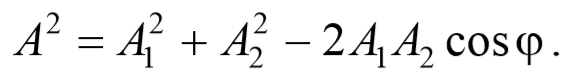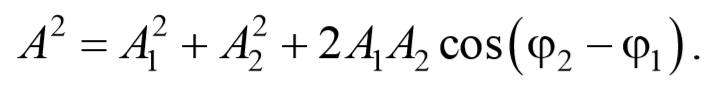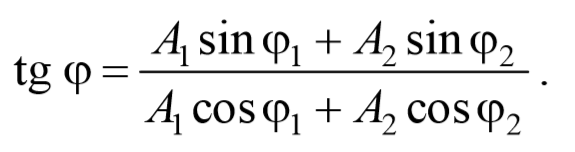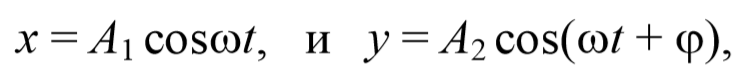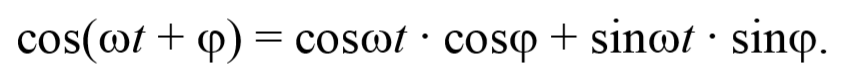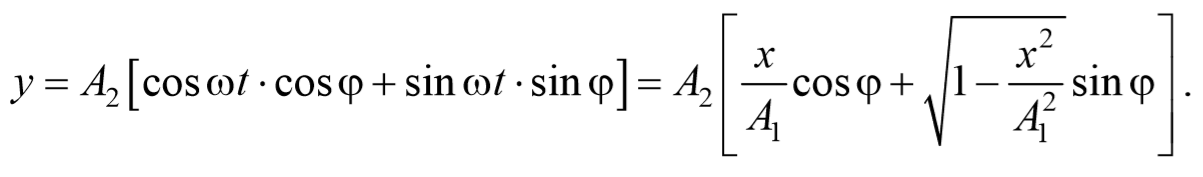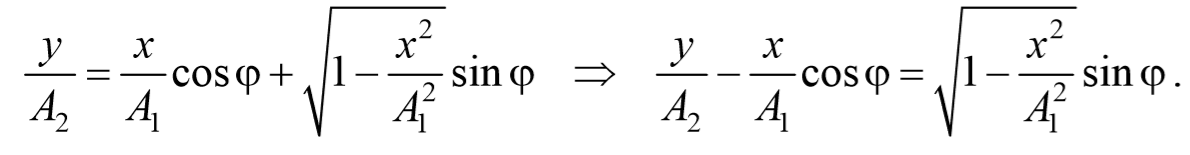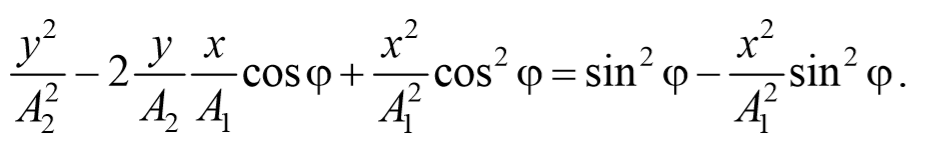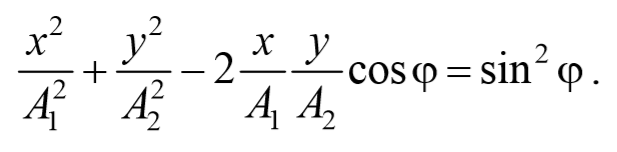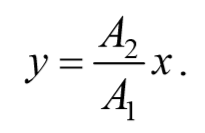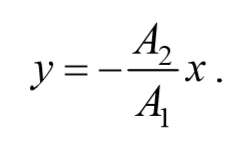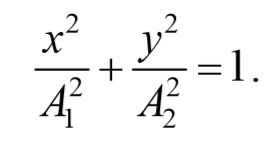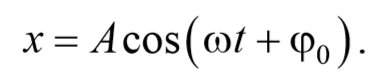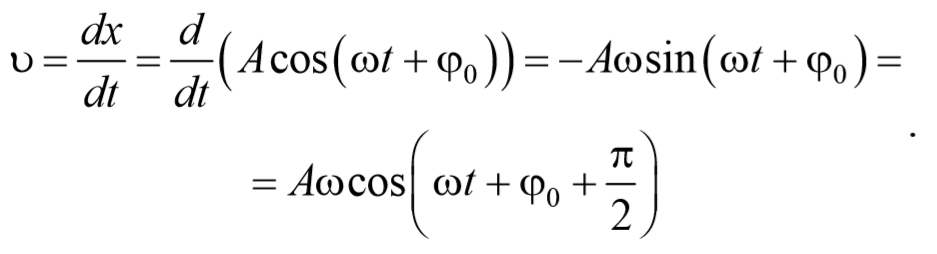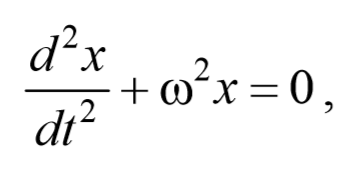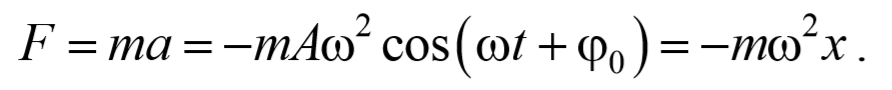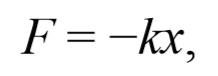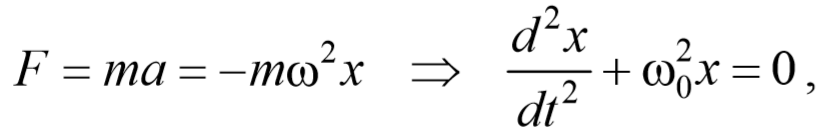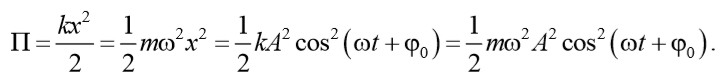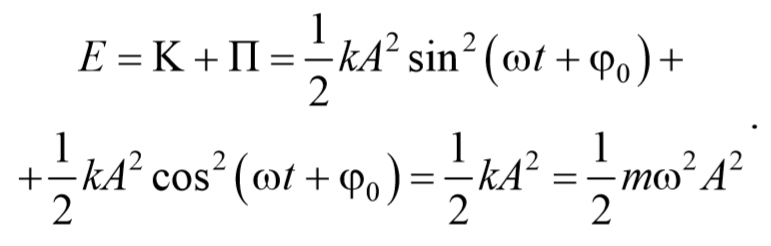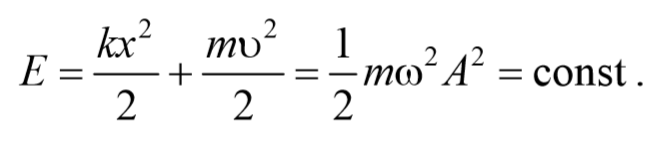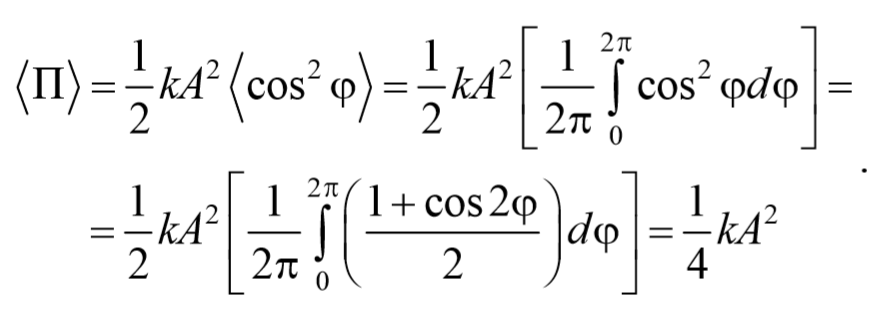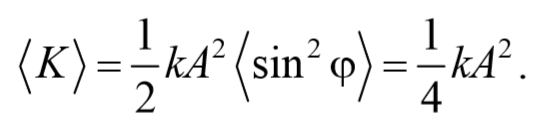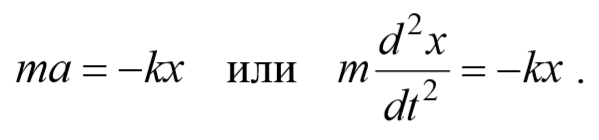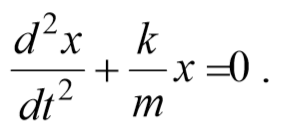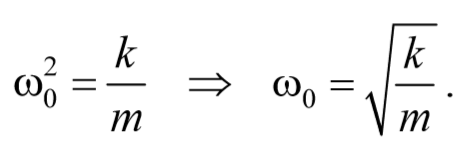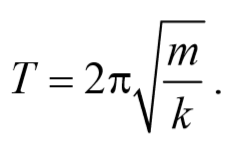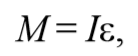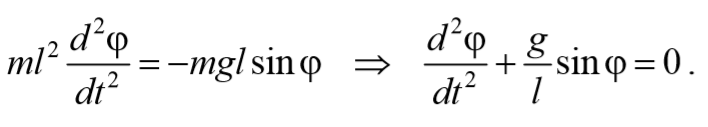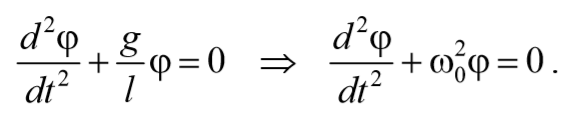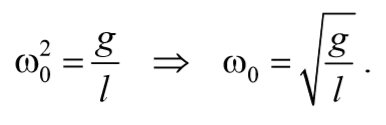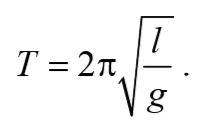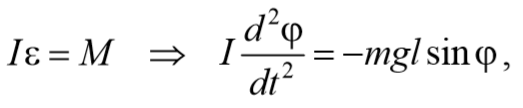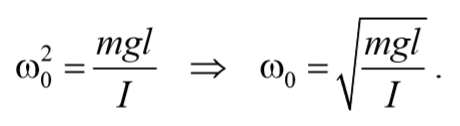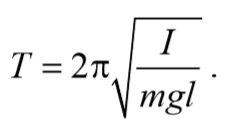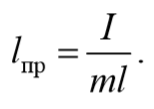Вывод дифференциального уравнения гармонических колебаний в колебательном контуре и его решение (6 видео)

Вывод дифференциального уравнения свободного колебания

На тело, совершающее свободные колебания, действуют две силы:

1. Сила, определяемая по второму закону Ньютона:

где m – масса тела;

а – ускорение;

х – смещение;

t – время.

2. Сила упругости, выраженная по закону Гука:

где k – коэффициент упругости. Знак минус показывает, что сила упругости F_упр всегда направлена в сторону положения равновесия.

На основании второго закона Ньютона (произведение массы тела на его ускорение равно сумме всех действующих сил) получаем:

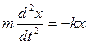
Перенесем –kx в левую часть равенства, получим:

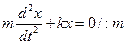
Введем замену: ,

где ω₀ – круговая (циклическая) частота колебаний (ω₀=2πν)

Получили дифференциальное уравнение второго порядка относительно смещения х.

Решением этого уравнения будет:

или (см. рис.1 и рис. 2).

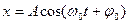
где А – амплитуда колебания;

φ₀ – начальная фаза;

ω₀t+φ₀ – фаза колебания в момент времени t;

ω₀t= ∆φ – изменение фазы колебания за время t.

Выведем уравнения мгновенной скорости и мгновенного ускорения, если колебания совершаются по закону косинуса.

Затухающие колебания.

Все реальные гармонические колебания происходят при воздействии сил сопротивления, на преодоление которых тело затрачивает часть своей энергии, в результате амплитуда колебания уменьшается со временем, т.е. колебания носят затухающий характер.

Представим график затухающего колебания:

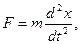
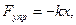
Вывод дифференциального уравнения затухающего колебания.На тело, кроме силы силы упругости действует сила сопротивления:

где r – коэффициент сопротивления.

Согласно второму закону Ньютона можно записать:

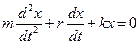
Разделим на массу m, получим:

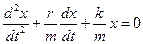
Введем обозначения: ,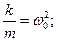

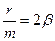
где β – коэффициент затухания.

Получили дифференциальное уравнение затухающего колебания:

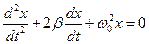
Решение уравнения существенно зависит от знака разности ,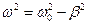

где ω— круговая частота затухающих колебаний, ω₀ — круговая частота собственных колебаний системы (без затухания).

При ω>0 решение дифференциального уравнения будет следующим:

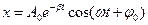
Амплитуда затухающего колебания в любой момент времени t определяется равенством:

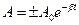
где А₀ – начальная амплитуда, указанная на графике (см. рис 3).

Период Т затухающих колебаний определяется по формуле:

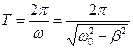
Скорость затухания (быстрота уменьшения амплитуды) определяется величиной коэффициента затухания β: чем больше β, тем быстрее уменьшается амплитуда.

Для характеристики скорости затухания ввели понятие декремента затухания.

Декрементом затухания называется отношение двух соседних амплитуд, разделенных периодом:

На практике степень затухания характеризуется логарифмическим декрементомзатухания λ, равным:

Выведем формулу, связывающую логарифмический декремент затухания λ с коэффициентом затухания β и периодом колебания Т.

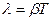
Выведем размерность коэффициента затухания

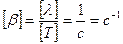
Вынужденные колебания. Вынужденными колебанияминазываются колебания, возникающие в системе при воздействии на неё внешней силы, изменяющейся по периодическому закону.

Пусть на систему действует сила:

где F₀ – максимальное значение,

ω — круговая частота колебаний внешней силы.

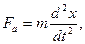
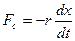
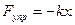
На систему действуют сила сила сопротивления и сила упругости .

С учетом всех четырех сил на основании второго закона Ньютона запишем:

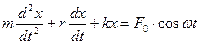
Разделим обе части равенства на m, получим:

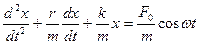
Получили дифференциальное уравнение вынужденного колебания:

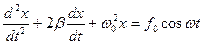
Представим график вынужденных колебаний:

Вывод дифференциального уравнения гармонических колебаний в колебательном контуре и его решение

В начале амплитуда колебаний возрастает, а затем становится постоянной А.

Для установившихся вынужденных колебаний:

(см. рис. 4)

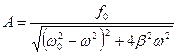
Резонанс.Если ω₀ и β для системы заданы, то амплитуда А вынужденных колебаний имеет максимальное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Достижение максимальной амплитуды вынужденных колебаний для заданных ω₀ и β называется резонансом.

Резонансная круговая частота определяется формулой:

а резонансная амплитуда:

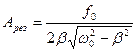
Если отсутствует сопротивление (β=0), то амплитуда неограниченно возрастает.

Представим на графиках зависимость амплитуды вынужденных колебаний от круговой частоты вынуждающей силы ω при различных значениях коэффициента затухания:

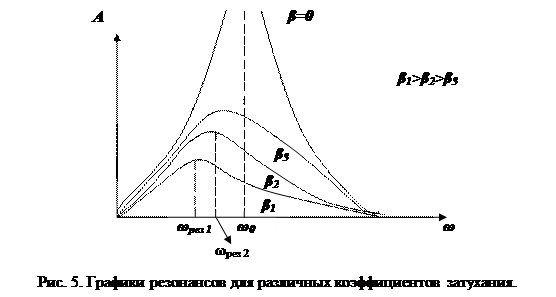По виду резонансной кривой резонанс может быть острым при β→0, тупым – при β→1. (см. рис. 5).

По механизму возбуждения резонанс классифицируется на:

— механический; акустический; электромагнитный; парамагнитный; ядерномагнитный.

Возникновение резонансных явлений в организме может быть как полезным, так и вредным. Например, на акустическом резонансе основано восприятия звука, инфразвук может вызвать разрыв тканей внутренних органов.

Автоколебания.При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды. Если восполнять эту потерю энергии, то колебания станут незатухающими. Пополнять эту потерянную системой энергию можно за счет источника энергии извне, а можно сделать так, чтобы колеблющаяся система сама бы управляла внешним воздействием.

Незатухающие колебания, возникающие в системе за счет источника энергии, не обладающего колебательными свойствами, называются автоколебаниями, а сами системы – автоколебательными.

Классическим примером автоколебаний являются часы: заведенная пружина; поднятая гиря – источник энергии; анкер – регулятор поступления энергии от источника; маятник или баланс – колебательная система.

Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы.

Автоколебания осуществляется по следующей схеме:

Через канал обратной связи регулятор, получив информацию о состоянии колебательной системы, осуществляет регулирующую подачи энергии от источника к системе.

К автоколебательным системам относятся сердце, легкие и т.д.

Автоколебательная система сердца может быть представлена в следующем виде:

Порядок выполнения работы:

Включить кимограф, записать положение равновесия.
Отклонив маятник в сторону, отпустить его, одновременно включив секундомер.
После записи последнего n-го колебания отключить секундомер.
После последнего колебания зарегистрировать положение равновесия и отключить кимограф.
Записать графики 3-го – 5-го колебательных процессов.
С помощью линейки для каждого графика определить величину начальной амплитуды (А₀) и последней амплитуды (А_n).
Подсчитать число полных колебаний на графике (n).
Определить период колебания T:

где t – время по секундомеру.

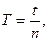
Определить величину коэффициента затухания по формуле:

Определить величину логарифмического декремента затухания: .
Полученные данные занести в таблицу.

п/п

А₀ (см)

А_n (см)

t(c)

T(c)

β(c -1 )

Контрольные вопросы

Определения и единицы измерения основных характеристик колебательного движения.
Гармонические колебания. Вывод дифференциального уравнения гармонического колебания и его решение.
Затухающие колебания. Вывод дифференциального уравнения затухающего колебания и его решение.
Декремент затухания, логарифмический декремент затухания. Вывод формулы, связывающей логарифмический декремент с периодом колебания и коэффициентом затухания.
Вынужденные колебания. Дифференциальное уравнение вынужденного колебания и его решение.
Резонанс и его значение в медицине.
Автоколебания.

Тестовые задания

Циклической (круговой) частотой называется число полных колебаний за:

а) 1 с; б) 1 мин; в) 1 ч; г) 2π с.

Укажите формулу, связывающую циклическую частоту ω с частотой ν:

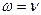
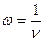
а) ; в) ;

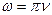
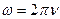
б) ; г) .

Укажите формулу, по которой определяется амплитуда затухающего колебания в любой момент времени t:

а) 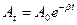; в) ;

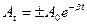
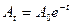
б) . г) .

Декрементом затухания называется отношение:

а) двух соседних амплитуд;

б) двух соседних амплитуд, разделенных периодом;

в) первой и последней амплитуд;

г) двух амплитуд, разделенных полупериодом.

Укажите единицу измерения коэффициента затухания β:

б) безразмерная величина; г) .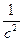

6. Укажите решение дифференциального уравнения свободного гармонического колебания:

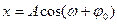
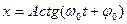
а) ; в) ;

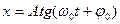
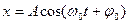
б) ; г) .

7. Укажите, сколько сил действует на систему, если она совершает свободные гармонические колебания:

8. Укажите дифференциальное уравнение свободного гармонического колебания:

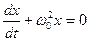
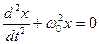
а) ; в) ;

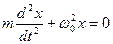
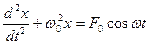
б) ; г) .

9. Укажите решение дифференциального уравнения затухающего колебания:

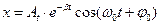
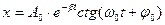
а) ; в) ;

б) 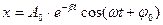; г) .

10. Сколько полных колебаний тело должно совершить в одну минуту, чтобы частота его колебаний равнялась 1 Гц:

11. Укажите подстановку в уравнение смещения затухающего колебания:

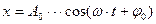
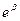
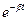
а) ; в) ;

б) ; г) ;

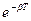
12. Укажите, сколько сил действует на систему, если она совершает вынужденные колебания:

13. Укажите дифференциальное уравнение вынужденного колебания:

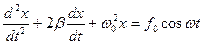
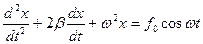
а) ; в) ;

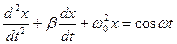
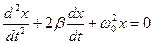
б) ; г) .

14. Укажите блок – схему, по которой осуществляются автоколебания:

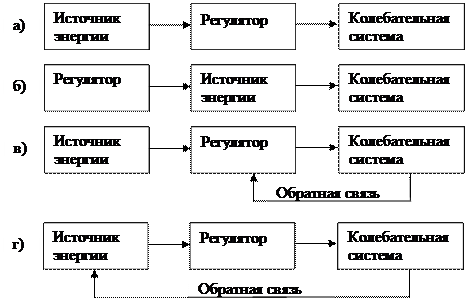15. Укажите формулу, связывающую логарифмический декремент затухания λ с периодом колебания Т и коэффициентом затухания β:

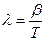
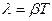
а) ; в) ;

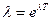
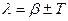
б) ; г) .

16. Укажите дифференциальное уравнение затухающего колебания:

а) ; в) ;

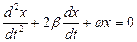
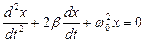
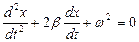
б) ; г) .

17. Укажите, по какой формуле определяется период колебания Т, если за время t тело совершило n полных колебаний:

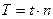
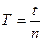
а) ; в) ;

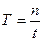
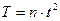
б) ; г) .

18. Укажите единицу измерения логарифмического декремента затухания:

б) с 2 ; г) безразмерная величина.

19. Укажите, какой параметр в уравнении смещения указывает на то, что процесс носит затухающий характер:

20. Укажите, какая сила вызывает уменьшение амплитуды при затухающих колебаниях:

а) ускоряющая сила;

б) сила упругости;

в) сила сопротивления;

г) сила давления.

21. Укажите, при каком значении декремента затухания процесс затухания будет проходить наиболее медленно:

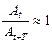
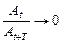
а) ; в) ;

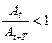
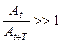
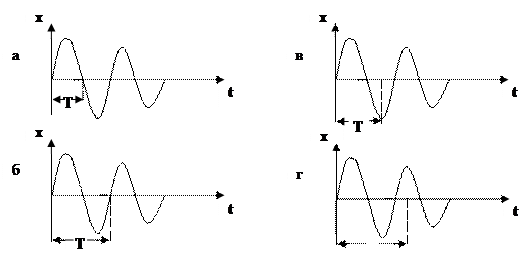
б) ; г) .

22. Укажите, на каком из графиков показан период колебания Т:

23. Укажите график вынужденного колебания:

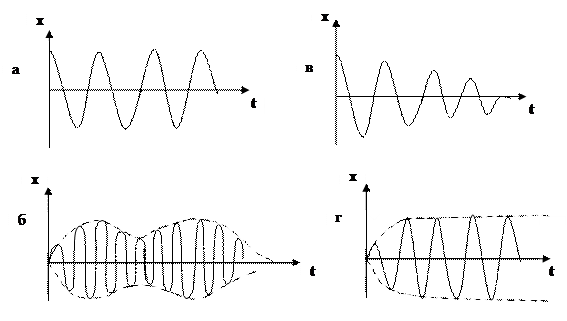24. Укажите, каков физический смысл знака «-» в формуле закона Гука

а) физический смысл отсутствует;

б) показывает, что направления силы упругости F_упр и смещения х совпадают;

в) показывает, что направления силы упругости F_упр и смещения х противоположны;

г) показывает, что направления силы упругости F_упр и смещения х взаимно перпендикулярны.

25. Частотой колебания ν называется величина, показывающая число полных колебаний:

а) за минуту; в) за час;

б) за секунду; г) за сутки.

26. Укажите, в каких единицах измеряется циклическая частота ω:

а) в секундах; в) в минутах;

б) в Гц ; г) в часах.

27. Укажите условие резонанса при β=0:

Содержание

Дифференциальное уравнение электромагнитных колебаний в электрическом колебательном контуре
Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
5.1. Свободные гармонические колебания и их характеристики.
5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.
5.3. Дифференциальное уравнение гармонических колебаний и его решение.
5.4. Энергия гармонических колебаний.
5.5. Пружинный, математический и физический маятники.
🎬 Видео

Видео:Урок 327. Гармонические колебанияСкачать

Дифференциальное уравнение электромагнитных колебаний в электрическом колебательном контуре

Свободные (собственные) колебания электрического заряда q на обкладках конденсатора и силы J электрического тока в электрическом колебательном контуре возникают, когда предварительно заряженный конденсатор замыкают на катушку с индуктивностью L (рис. 175).

Силу J электрического тока можно считать одинаковой во всех частях контура в каждый момент времени t, если выполняется условие, что электромагнитное поле распространяется в пространстве со скоростью, равной скорости света с в вакууме

где I — линейные размеры контура, с — скорость света в вакууме, v — частота колебаний.

Переменный электрический ток, для которого выполняется данное условие, называют квазистационарным. Колебательный контур можно рассматривать, как разомкнутую электрическую цепь, концами её являются обкладки конденсатора.

Пусть в некоторый момент времени t электрический заряд на обкладках конденсатора равен q (t), а разность потенциалов (

Для участка электрической цепи 1 — L — 2 (рис. 175) запишем закон Ома, согласно которому произведение силы J электрического

тока на электрическое сопротивление R участка цепи равно сумме разности потенциалов (рр/ — 1 — циклическая частота свободных колебаний в контуре.

Согласно уравнению (19.35) сила / электрического тока опережает электрический заряд q по фазе на Д. В момент времени t,

когда сила J электрического тока в контуре максимальна (J = J _мах), электрический заряд q на обкладках конденсатора равен нулю (q = 0) и наоборот.

Напряжение U на конденсаторе со временем t изменяется по гармоническому закону, совпадая по фазе с электрическим зарядом q

где U _мах = ^ >»‘ амплитуда колебаний напряжения U (разности

Электродвижущая сила самоиндукции ? _с, а так же и энергии электрического Wи магнитного IV „_а,,„ поля изменяются со временем, совершая гармонические колебания, описываемые формулами

где ? с.мах = Ц мах ю₀ 2 — L- амплитуда колебаний ЭДС самоиндукции.

Полная энергия W _полн, сосредоточенная в колебательном контуре, описывается в любой момент времени t уравнением

Здесь учли, что со₀ = 1 и sin (со₀-Г + 1 с учётом, что J 2 _х = col ? q 2 ,

получим

Максимальные значения энергии электрического поля в конденсаторе достигаются в моменты времени, когда энергия магнитного поля катушки индуктивности равна нулю.

Согласно закону сохранения полной энергии, в колебательном контуре выполняется равенство

или

Итак, колебательный процесс в контуре характеризуется периодическим переходом энергии электрического поля конденсатора в энергию магнитного поля катушки. Полная энергия колебательного контура в моменты времен t = 0, t = Т, t = 2Т и т. д. сосредоточена в

электрическом поле конденсатора, а в моменты времени t = Z. t = 1 Г,

t = 5 т и т. д .в магнитном поле катушки индуктивности. В

колебательном контуре дважды за период Т колебаний происходит перекачка энергии из электрического поля конденсатора в магнитное поле катушки индуктивности и обратно.

В начальный момент времени (t =0) на обкладках заряженного конденсатора размещается максимальный электрический заряд q (q = q _лшх) и энергия электрического поля имеет максимальную величину

Сила J электрического тока равна нулю (У = 0).

Сравним параметры свободных механических колебаний пружинного маятника и свободных электромагнитных колебаний в электрическом колебательном контуре (табл.4).

Тело массой m пружинного маятника в начальный момент времени (t =0) максимально удалено от положения равновесия Поэтому потенциальная энергия W упруго деформированной пружины имеет максимальное значение

Энергия электрического поля конденсатора является аналогом потенциальной энергии деформированной пружины пружинного маятника. Сила У электрического тока в колебательном контуре в момент времени t = >_Т достигает максимального значения (У = J _мах), 4

энергия магнитного поля в катушке с индуктивностью L максимальна (W = W_{маг мах}), а электрический заряд q на обкладках

конденсатора равен нулю (q = 0). Электрический ток не прекращается в контуре за счёт наличия катушки индуктивности и при отсутствии электрического заряда на обкладках.

Тело массой m пружинного маятника, движущееся под действием силы упругости к положению равновесия, в момент времени t = ф Т

проходит его по инерции с максимальной скоростью, имея максимальную кинетическую энергию W _мах, равную

Отсюда следует, что энергия магнитного поля катушки индуктивности является аналогом кинетической энергии пружинного маятника, а индуктивность L катушки аналогична массе т тела пружинного маятника.

Величина (J_), обратная ёмкости С конденсатора, аналогична

коэффициенту жёсткости к пружины.

Параметры свободных механических колебаний пружинного маятника и свободных электромагнитных колебаний в электрическом колебательном контуре

Электрический заряд конденсатора q

Скорость движения тела г = ^ х

Сила электрического тока _J=dq dt

Скорость изменения силы

Потенциальная энергия упруго деформированной пружины

Энергия электрического поля

Кинетическая энергия движущего тела массы

Энергия магнитного поля катушки индуктивности

Индуктивность катушки L

Коэффициент жёсткости пружины к

Величина, обратная ёмкости конденсатора — 1

Частота собственных колебаний

Частота собственных электромагнитных колебаний

Видео:5.4 Уравнение гармонических колебанийСкачать

Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.1. Свободные гармонические колебания и их характеристики.

Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.

Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид

1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.

2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.

3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [T] = 1 с .

За период система совершает одно полное колебание.

4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ν]= 1 Гц . Частота определяется по формуле

5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2π циклов колебаний, [ω]= с -1 . Циклическая частота связана с периодом и частотой колебаний соотношением

6) Фаза колебаний ωt + φ₀ − фаза указывает местоположение колеблющейся точки в данный момент времени.

7) Начальная фаза φ₀ − указывает местоположение колеблющейся точки в момент времени t = 0 .

5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.

Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.

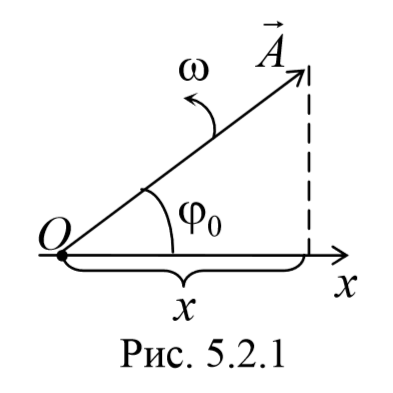
Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды А . Для этого из произвольной точки O , выбранной на оси Ox , под углом φ₀ , равным начальной фазе колебания, откладывается вектор амплитуды А . Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ox и принимать значения от -A до +A , а колеблющаяся величина изменяться со временем по закону x = Acos(ωt + φ₀)

1. Сложение одинаково направленных гармонических колебаний.

Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x₁ и x₂ , которые запишутся следующим образом:

Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор А . Проекция этого вектора на ось Ox равна сумме проекций слагаемых векторов x=x₂+x₂ , следовательно, вектор А представляет собой результирующее колебание. Определим результирующий вектор амплитуды А потеореме косинусов

Так как угол между векторами А ₁ и А ₂ равен φ=π-(φ₂-φ₁) , то cos[π-(φ₂-φ₁)]=-cos(φ₂-φ₁) , следовательно, результирующая амплитуда колебания будет равна

Определим начальную фазу результирующего колебания.

Из рисунка видно, что начальная фаза результирующего колебания

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.

2. Сложение взаимно перпендикулярных гармонических колебаний.

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X , так и вдоль оси Y . Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид

где φ − разность фаз обоих колебаний.

Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: cosωt= $$xover A_1$$ , а sinωt= $$sqrt=sqrt$$ Разложим косинус во втором из уравнений (5.2.6)

Перепишем это уравнение в следующем виде

После преобразования, получим

Используя тригонометрическое тождество cos 2 φ+sin 2 φ=1 , окончательно получим

Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.

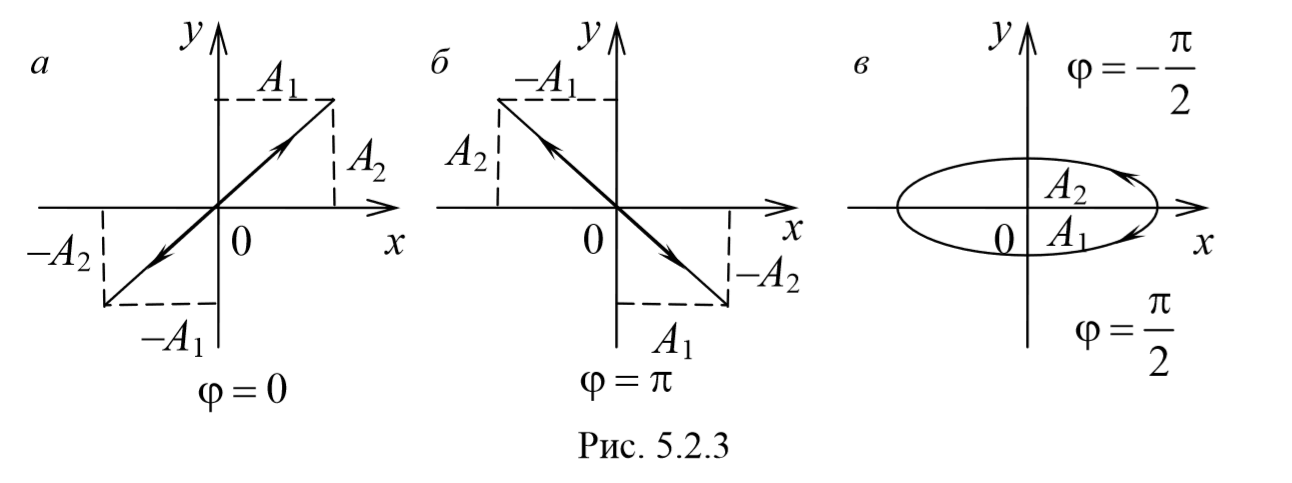
Рассмотрим несколько частных случаев и определим форму траектории для них:

a) разность фаз равна нулю [φ=0]

В этом случае $$( — )^2=0$$ , откуда получается уравнение прямой

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$A= sqrt<A_1+A_2>$$ .

2) разность фаз равна ±π[φ=±π] .

В этом случае $$( — )^2=0$$ , откуда получается уравнение прямой

3) Разность фаз равна ± $$πover 2$$ [φ=± $$π over2$$ ] . Тогда

Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи φ=+ $$πover 2$$ и φ=- $$πover 2$$ отличаются направлением движения. Если φ=+ $$πover 2$$ , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=-A₂sinωt и движение совершается по часовой стрелке. Если φ=- $$πover 2$$ , , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=A₂sinωt и движение совершается против часовой стрелке.

Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис

4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу . Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.

На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.

По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.

5.3. Дифференциальное уравнение гармонических колебаний и его решение.

Продифференцируем по времени уравнение гармонических колебаний

и получим выражение для скорости

Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2 . Амплитуда скорости равна Аω .

Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения

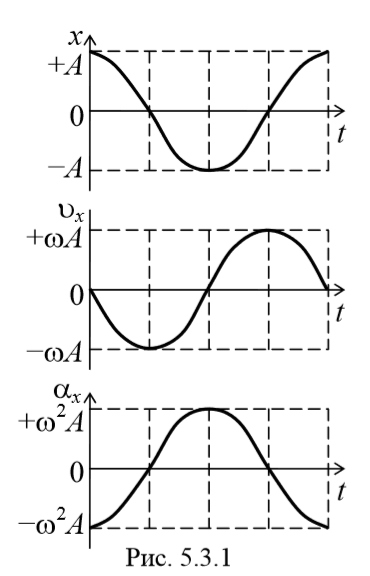
Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).

Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний

Результирующая сила, действующая на материальную точку массой m , определяется с помощью второго закона Ньютона. Проекция этой силы

Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой . Таким образом, гармонические колебания происходят под действием силы F , пропорциональной смещению x и направленной к положению равновесия,

где k=mω 2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами .

Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором . Ее динамическое поведение описывается дифференциальным уравнением

ω₀ − собственная частота осциллятора.

Решение этого уравнения дает закон движения линейного осциллятора x=Acos(ωt+φ₀) .

5.4. Энергия гармонических колебаний.

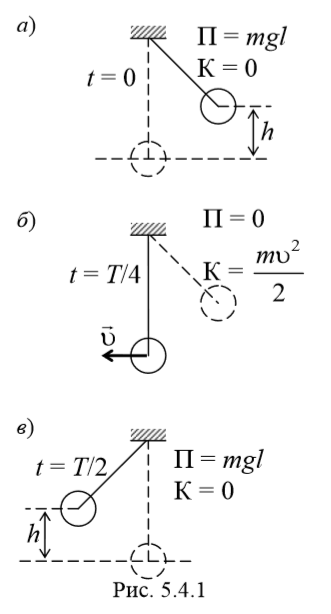
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.

Потенциальная энергия тела, совершающего гармонические колебания равна

Кинетическая энергия тела, совершающего гармонические колебания равна

Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом

Следовательно, полная энергия гармонического колебания

оказывается постоянной в случае гармонических колебаний.

Найдем среднее значение потенциальной энергии за период колебания

Аналогично получается для среднего значение кинетической энергии

Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2

5.5. Пружинный, математический и физический маятники.

Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.

1) Пружинный маятник − это материальная точка массой m , подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m , прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Ox F_упр=ma . Упругая сила F_упр=-kx . Приравнивая последние два уравнения и, используя определение ускорения тела, получим

Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой

Так как период колебаний определяется по формуле T= $$2πover ω_0$$ , то период колебаний пружинного маятника

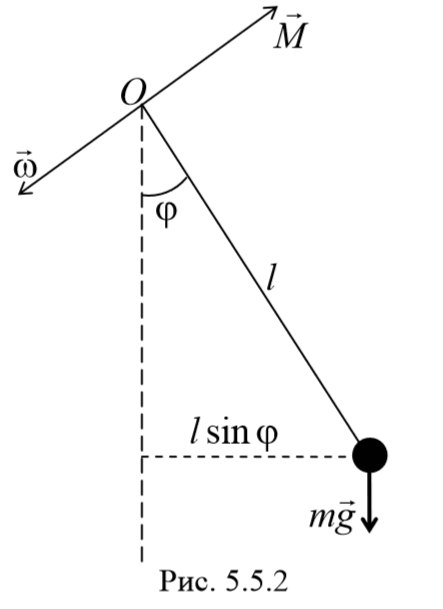
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m . Отклонение маятника от положения равновесия будем характеризовать углом φ , образованным нитью с вертикалью.

При отклонении маятника от положения равновесия возникает вращательный момент M , равный по величине mqlsinφ .Он имее акое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=-mqlsinφ . Применим основно ательного движения

где L=ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение ε= $$d^2φover dt^2$$ , получим

Если рассматривать малые колебания, то sinφ≈φ . Получим

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

Период колебаний математического маятника

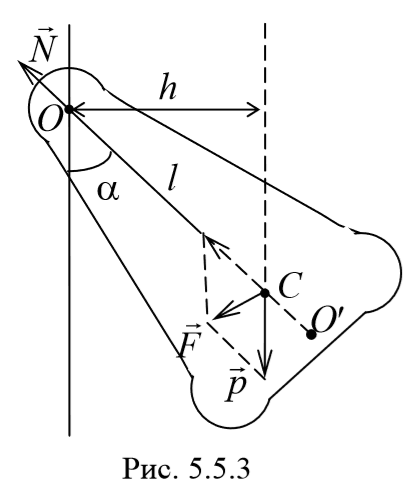
3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M=-mglsinφ .

Согласно основному уравнению динамики вращательного движения получаем

где I − момент инерции маятника относительно оси, проходящей через точку подвеса.

Если рассматривать малые колебания, то sinφ≈φ . Получим

Период колебаний математического маятника

Из сопоставления формул периодов колебаний математического и физического маятников T=2π $$sqrt$$ и T=2π $$sqrt$$ получается, что математический маятник с длиной

будет иметь такой же период колебаний, что и данный физический маятник.

Величина l_пр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.