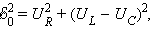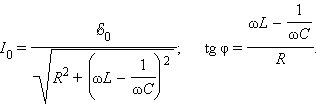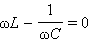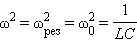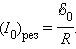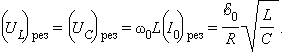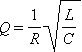В реальной колебательной системе можно получить незатухающие колебания, если колебания совершаются системой под действием вынуждающей силы, изменяющейся по гармоническому закону с частотой со:
где F0 — амплитуда внешней силы.
Тогда уравнение второго закона Ньютона (3.3), учитывая силу трения или сопротивления среды FTf) — —rx и возмущающую силу (7.29), имеет вид
Введем обозначения — = со0, -— = (3 и получим дифференциальное m 2m
уравнение вынужденных колебаний
где (3 — коэффициент затухания; со0 — собственная частота колебаний системы.
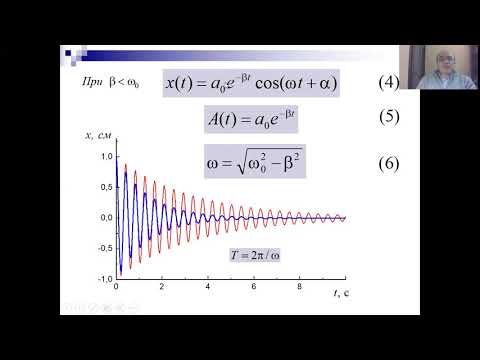
На рис. 7.9 изображен простейший случай установления вынужденных колебаний.
Рис. 7.9. Процесс установления вынужденных колебаний
Дифференциальное уравнение (7.31) является линейным неоднородным уравнением. Из теории линейных дифференциальных уравнений с постоянными коэффициентами известно, что его решение равно сумме общего решения соответствующего однородного (с нулевой правой частью) уравнения (типа (7.21)) и частного решения неоднородного уравнения.
Общее решение однородного уравнения (7.21) нам известно:
где со’ = л/соо — (З 2 — собственная частота затухающих колебаний.
Можно показать, что частное решение имеет вид
где А — амплитуда вынужденных колебаний; ср — отставание по фазе вынужденных колебаний от колебаний вынуждающей силы.
Таким образом, осциллятор одновременно совершает два типа колебаний (7.32) и (7.33) и общее решение уравнения (7.31) есть сумма решений:
Слагаемое (7.32) играет заметную роль только в начальной стадии процесса при установлении колебаний (рис. 7.9). Со временем затухающие колебания быстро затухают вследствие сопротивления среды: из-за экспоненциального множителя е
Р’ роль решения а:, уменьшается и им можно пренебречь по истечении некоторого времени. В решении уравнения вынужденных колебаний (7.31) при установившихся колебаниях остается только слагаемое (7.33), т.е. колебания происходят с постоянной амплитудой и, следовательно, не затухают. При этом время установления стационарного режима вынужденных колебаний после начала действия вынуждающей силы равно т.
Определим постоянные А и ф. Для этого продифференцируем уравнение (7.33) дважды по времени:
Видео:Вынужденные колебания и дифференциальное уравнениеСкачать
Вынужденные колебания
Видео:71. Вынужденные колебанияСкачать
Определение вынужденных колебаний
Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.
Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.
Видео:Урок 343. Затухающие колебания (часть 1)Скачать
Дифференциальное уравнение вынужденных колебаний
Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:
Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:
где $x$ — координата; $delta $ — коэффициент затухания; $_0$ — циклическая частота свободных незатухающих колебаний (если $delta $=0, то $_$называют собственной частотой колебаний).
Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:
где $q$ — заряд; $delta =frac$ — коэффициент затухания; $_0=frac<sqrt>$; $U=U_m$ — внешнее переменное напряжение.
Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:
где $s$ — колеблющийся параметр; $x_0=frac$ если колебания механические ($x_0=frac— в случае электрических колебаний$).
Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:
Его общее решение:
где $A_0$ — начальная амплитуда колебаний.
Частное решение уравнения (4) в представлено выражением:
Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).
Установившись, вынужденные колебания происходят с частотой $omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $omega $.
Видео:Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать
Резонанс вынужденных колебаний
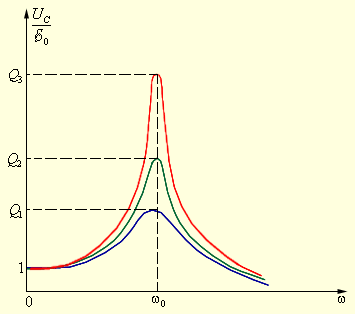
Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.
Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(omega )$. Взяв производную $frac$ и приравняв ее к нулю получим:
Равенство (10) справедливо при:
Получается, что резонансная частота ($_r$) равна:
При $^2ll ^2_0$ резонансная частота совпадает с собственной частотой колебаний $_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:
При небольшом затухании колебаний (если $^2ll ^2_0$) амплитуда при резонансе равна:
где $Q=frac<_0>$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать
Примеры задач с решением
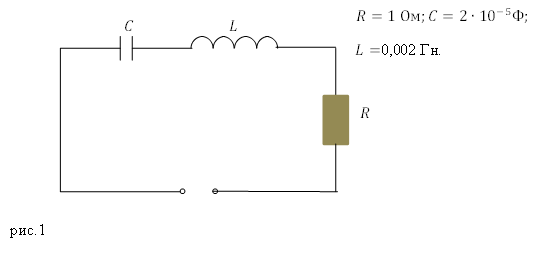
Задание. Какова добротность колебательного контура, представленного на рис.1?
Решение. Добротность электрического колебательного контура найдем как:
При этом собственная частота колебаний в таком контуре равна:
коэффициент затухания находим как:
Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:
Ответ. $Q=10$
Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?
Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:
где коэффициент затухания равен $delta =frac$. Из функции, которая задает вынуждающую силу:
мы видим, что амплитуда силы равна единице:
Собственная частота колебаний груза на пружине:
Амплитуда при резонансе таких колебаний равна:
Видео:Честный вывод уравнения колебанийСкачать
12 вынужденные колебания дифференциальное уравнение его решение график векторная диаграмма
Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями .
Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими . Внешний источник периодического воздействия обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.
Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω0.
Если частота ω0 свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте ω внешнего источника .
Для установления вынужденных стационарных колебаний после включения в цепь внешнего источника необходимо некоторое время Δ. Это время по порядку величины равно времени τ затухания свободных колебаний в цепи.
Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического источника тока, называются цепями переменного тока .
Рассмотрим последовательный колебательный контур, то есть -цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рис. 2.3.1):
 , |
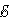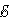
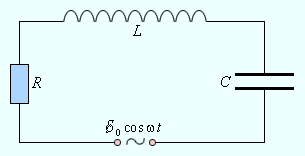где 0 – амплитуда, ω – круговая частота.
 | |||||||||||||||||||||||||||||
| Рисунок 2.3.1. Предполагается, что для электрической цепи, изображенной на рис. 2.3.1, выполнено условие квазистационарности. Поэтому для мгновенных значений токов и напряжений можно записать закон Ома:
Величина Уравнение вынужденных колебаний можно записать в виде
где , и – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами , и . При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока. Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм . На векторной диаграмме колебания определенной заданной частоты ω изображаются с помощью векторов (рис. 2.3.2).
|
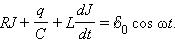
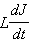– это ЭДС самоиндукции катушки, перенесенная с изменением знака из правой части уравнения в левую. Эту величину принято называть напряжением на катушке индуктивности .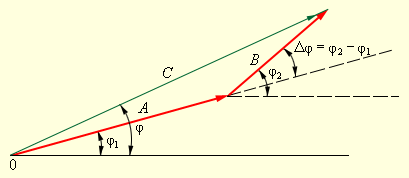
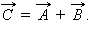
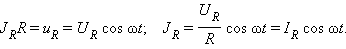
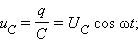
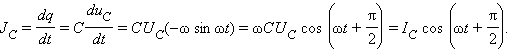
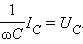
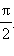
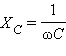называется емкостным сопротивлением конденсатора .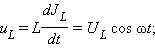
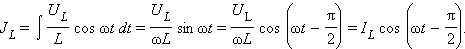
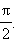
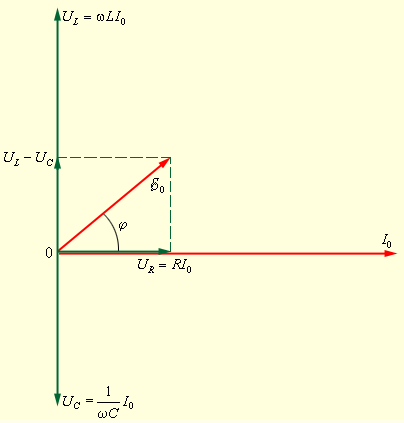
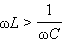или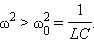 
В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.
