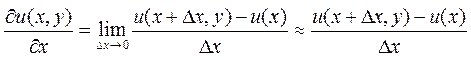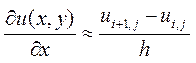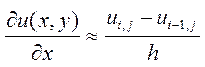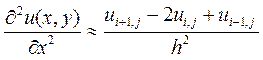Читайте также:
|
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
7.1 Метод сеток для решения смешанной задачи для уравнения параболического типа (уравнения теплопроводности)
Смешанная задача означает, что следует найти искомую функцию, удовлетворяющую заданному уравнению в частных производных, краевым, а так же начальным условиям.
Рассмотрим смешанную задачу для однородного уравнения теплопроводности

Задано начальное условие
и заданы краевые условия первого рода
Требуется найти функцию u (x,t) , удовлетворяющую в области D (0 x 

Рисунок 10 – Неявная схема
При проведении замены 

Приближенное значение искомой функции в точке 





j =0,1. m ; 
Заменим производные разностными отношениями


В результате получим неявную двухслойную схему с погрешностью O ( +h 2 )

Используя подстановку 

где: u 0, j = 1 ( t j ) ; u n , j = 2 ( t j ) .
Получаем разностную схему, которой аппроксимируем уравнение (7.4). Эта схема (7.7) неявная, и выглядит так, как показано на рисунке 10. При построении схемы (7.7) получается система линейных уравнений с трехдиагональной матрицой. Решив ее любым способом (в частности, методом прогонки), получаем значения функции на определенных временных слоях. Так, на нулевом временном слое используем начальное условие U i,0 =f ( x i ), т.к. j =0. Эта неявная схема более устойчива для любых значений параметра >0.
Есть и явная схема (рисунок 11), но она устойчива только при 

Рисунок 11 — Явная схема
7.2 Решение задачи Дирихле для уравнения Лапласа методом сеток
Рассмотрим уравнение Лапласа

Уравнение (7.8) описывает распространение электромагнитных волн(полей). Будем рассматривать уравнение Лапласа в прямоугольной области 




где 
Введем обозначения u ij = u ( x i , y j ). Накладываем на прямоугольную область сетку 



Частные производные аппроксимируем по формулам
и заменим уравнение Лапласа конечно-разностным уравнением
Рисунок 12 – Схема “крест”

где: i =1,…, n -1, j =1. m -1 (т.е. для внутренних узлов).
Погрешность замены дифференциального уравнения разностным составляет величину О(
Получаем систему (7.10) линейных алгебраических уравнений, которые можно решить любым итерационным методом (Зейделя, простых итераций и т.д.). При этом построении системы использовалась схема типа “крест”(рисунок 12). Строим последовательность итераций по методу Гаусса-Зейделя

где s -текущая итерация.
Условие окончания итерационного процесса

Условие (7.11) ненадежно и на практике используют другой критерий
где 
Схема “крест “- явная устойчивая схема ( малое изменение входных данных ведет к малому изменению выходных данных).
7.3 Решение смешанной задачи для уравнения гиперболического типа методом сеток
Рассмотрим уравнение колебания однородной и ограниченной струны.
Задача состоит в отыскании функции u ( x , t ) при t >0, удовлетворяющей уравнению гиперболического типа

где: 0 x a ; 0 t
 |
По определению частная производная равна
Если рассматривать функцию только в узлах сетки, то частную производную можно записать в форме
где узел 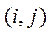
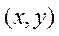
Полученное выражение называется правой конечной разностью. Название связано с тем, что для вычисления производной в точке используются значение функции в этой точке и точке, лежащей правее. Очевидно, что сходное выражение можно было бы получить, используя точку, лежащую слева.
Такое выражение называется левой конечной разностью. Можно получить центральную конечную разность, найдя среднее этих выражений.
Теперь получим выражения для вторых производных.
В данном случае для нахождения производной мы использовали симметричные точки. Однако, очевидно, можно было бы использовать точки с несимметричным расположением.
Заменяя производные, входящие в уравнение (*) разностными отношениями, получим конечно-разностные уравнения
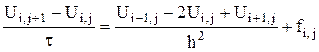
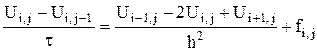
Эти уравнения аппроксимируют исходное дифференциальное уравнение в узле сетки (хi, уi) с погрешностью порядка О(h 2 +t).
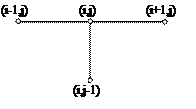
 |
Начальные и граничные условия определяют значения сеточной функции в граничных узлах:
Тогда во внутренних точках сетки решение можно искать в явном виде по схеме (из уравнения (**)
🎦 Видео
Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Решение задачи теплопроводности методом конечных разностейСкачать
Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

Решение задач теплопроводности (короткая версия)Скачать

Решение задач теплопроводности (часть 2)Скачать

Метод сеткиСкачать

Тихонов Н. А. - Основы математического моделирования - Метод конечных разностей (Лекция 7)Скачать

Уравнение теплопроводности на полупрямой (решение задачи)Скачать

6-1. Уравнение теплопроводностиСкачать

8.1 Решение уравнения теплопроводности на отрезкеСкачать

Решение задачи теплопроводности (Явная разностная схема)Скачать

Численные методы математической физики - Решение смешанной задачи для уравнения теплопроводностиСкачать

Численное решение уравнения теплопроводностиСкачать
Уравнение в частных производных Уравнение теплопроводностиСкачать

Метод конечных элементов (Часть 1) | Пример реализации для уравнения теплопроводностиСкачать

Метод Фурье для неоднородного уравнения теплопроводностиСкачать

 со следующими начальными и граничными условиями:
со следующими начальными и граничными условиями:  ,
,  ,
,  ,
,  ,
,  .
. , j = 1, . , n , ( 10 )
, j = 1, . , n , ( 10 ) , n — число узлов cетки по x. ( 11 )
, n — число узлов cетки по x. ( 11 )















 сетку
сетку  ; i = 0,1,…, n ;
; i = 0,1,…, n ;  ;
;  ; j =0,1,…, m ; m = T .
; j =0,1,…, m ; m = T . .
. ,
, ,
,  для всех j .
для всех j . решения u ( x , t ) в узлах
решения u ( x , t ) в узлах  при i =1,…, n ; j = 1,…, m . Алгоритм решения основан на том, что решение на каждом следующем слое ( j = 2,3. n ) можно получить пересчетом решений с двух предыдущих слоев ( j = 0,1. n — 1) по формуле (7.16). При j =0 решение известно из начального условия
при i =1,…, n ; j = 1,…, m . Алгоритм решения основан на том, что решение на каждом следующем слое ( j = 2,3. n ) можно получить пересчетом решений с двух предыдущих слоев ( j = 0,1. n — 1) по формуле (7.16). При j =0 решение известно из начального условия  . Для вычисления решения на первом слое ( j = 1) положим
. Для вычисления решения на первом слое ( j = 1) положим ,
, , i = 1,2,…, n . Теперь для вычисления решений на следующих слоях можно использовать формулу (7.16).
, i = 1,2,…, n . Теперь для вычисления решений на следующих слоях можно использовать формулу (7.16). .
.




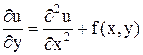 , (*)
, (*)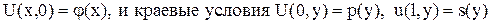 ,
,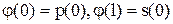 .
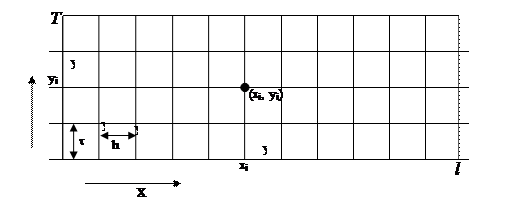
.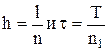 . Через точки деления проведём прямые , параллельные соответствующим осям. В результате область D разобьётся на прямоугольники с вершинами (хi, yi), где xi=(i-1)h, i=1,n+1, уi=(j-1)×t, i=1,n1+1.
. Через точки деления проведём прямые , параллельные соответствующим осям. В результате область D разобьётся на прямоугольники с вершинами (хi, yi), где xi=(i-1)h, i=1,n+1, уi=(j-1)×t, i=1,n1+1.