Метод гармоник исследования устойчивости разностных схем для уравнения переноса

Для уравнения (4.22) рассмотрим пять разностных схем, шаблоны которых показаны на рис. 4.13: явный уголок вперед (рис. 4.13, а), явный уголок назад (рис. 4.13, б), явная схема второго порядка точности (рис. 4.13, в), явная схема Лакса (рис. 4.13, г) и неявный уголок назад (рис. 4.13, д). Светлыми точками выделены узлы, в которых решение известно, темными — узлы, в которых требуется определить решение.

Выпишем некоторые вспомогательные формулы:

По формуле (4.23) разностная схема для явного уголка вперед имеет вид

Преобразуем схему (4.23) с учетом соотношений (4.30) к виду

и с использованием формул (4.29) — к виду Для квадрата модуля X имеем соотношение

из которого следует, что |Л| > 1 при любых т и Л, т. е. разностная схема (4.23) — явный уголок вперед — абсолютно неустойчива. Этот же результат был получен ранее из других соображений.

JIAKC ПЕТЕР Д. (Lax Peter D.; 1926) — американский математик, чьи основные труды относятся к теории дифференциальных уравнений с частными производными, функциональному анализу и прикладной математике. В вычислительной математике известен метод Лакса — Вендорфа для численного решения задачи одномерного нестационарного истечения идеального газа.

Выкладки, аналогичные проведенным для явного уголка вперед, дают

Из этого соотношения следует, что разностная схема (4.25) — явный уголок назад, как это было показано и ранее, условно устойчива при т/Л [1] .

Рассмотрим явную схему второго порядка точности, про- иллюстированную рис. 4.13, в, в которой производная по х аппроксимируется со вторым порядком точности, т. е. отброшены члены малости 0(т, Л 2 ). Разностная схема имеет вид

а для квадрата модуля X может быть получено соотношение

Для явного уголка назад (рис. 4.13,6) разностная схема по формуле (4.25) имеет вид

Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Устойчивость. Исследование устойчивости методом гармонического анализа.

конечно-разностная схема устойчива, если для малых возмущений входных данных (начально-краевых условий и правых частей) конечно-разносная схема обеспечивает малые возмущения сеточной функции u_h т.е. решение с помощью конечно-разностной схемы находится под контролем входных данных.

Если во входные данные f_n входят только начальные условия или только краевые условия, или только правые части, то говорят об устойчивости соответственно по начальным условиям, по краевым условиям или по правым частям.

Из математической физики известно, что решение начально-краевых задач представляется в виде следующего ряда:

, (16)

где λ_n – собственные значения

– собственные значения функции, получаемые из решения соответствующей задачи Штурма-Лиувиля, т.е. решение может быть представлено в виде суперпозиции отдельных гармоник , каждая из которых есть произведение функции времени и функции пространственной переменной, причем последняя по модулю ограничена сверху единицей при любых значениях переменной x.

В то же время функция времени , называемая амплитудной частью гармоники, никак не ограничена, и, по всей вероятности, именно амплитудная часть гармоник является источником неконтролируемого входными данными роста функции и, следовательно, источником неустойчивости.

Таким образом, если конечно-разностная схема устойчива, то отношение амплитудной части гармоники на верхнем временном слое к амплитудной части на нижнем временном слое по модулю должно быть меньше единицы.

Если разложить значение сеточной функции в ряд Фурье по собственным функциям:

(17)

где амплитудная часть может быть представлена в виде произведения

(18)

где – размерный и постоянный сомножитель амплитудной части,

k – показатель степени (соответствующий номеру временного слоя) сомножителя, зависящего от времени.

Тогда подставив (17) в конечно-разностную схему, можно по модулю оценить отношение амплитудных частей на соседних временных слоях.

Однако поскольку операция суммирования линейна и собственные функции ортогональны для различных индексов суммирования, то в конечно-разностную схему вместо сеточных значений достаточно подставить одну гармонику разложения (17) (при этом у амплитудной части убрать индекс n), т.е.

(19)

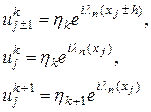
Таким образом, если конечно-разностная схема устойчива по начальным данным, то

, (20)

т. е. условие (20) является необходимым условием устойчивости.

Схема Кранка-Николсона

Явная конечно разностная схема, записанная в форме

(21)

обладает тем достоинством, что решение на верхнем временном слое t_k+l полу-

чается сразу (без решения СЛАУ) по значениям сеточной функции на нижнем временном слое t k , где решение известно (при k = 0 значения сеточной функции формируются из начального условия). Но эта же схема обладает существенным недостатком, поскольку она является условно устойчивой.

С другой стороны, неявная конечно-разностная схема, записанная форме

(22)

приводит к необходимости решать СЛАУ, но зато эта схема абсолютно устойчива.

Проанализируем схемы (21) и (22). Пусть точное решение, которое неизвестно, возрастает по времени, т.е. . Тогда, в соответствии с явной схемой (21), разностное решение будет заниженным по сравнению с точным, так как определяется по меньшим значениям сеточной функции на предыдущем временном слое, поскольку решение является возрастающим по времени.

Для неявной схемы (22) на возрастающем решении, наоборот, решение завышено по сравнению с точным, поскольку оно определяется по значениям сеточной функции на верхнем временном слое.

На убывающем решении картина изменяется противоположным образом: явная конечно-разностная схема завышает решения, а неявная — занижает (Рисунок 4).

На основе этого анализа возникла идея о построении более точной неявно-явной конечно-разностной схемы с весами при пространственных конечно-разностных операторах, причем при измельчении шагов тик точное (неизвестное) решение может быть взято в «вилку» сколь угодно узкую, так как если явная и неявная схемы аппроксимируют дифференциальную задачу и эти схемы устойчивы, то при стремлении сеточных характеристик τ и h к нулю решения по явной и неявной схемам стремятся к точному решению с разных сторон.

Рисунок 4 – Двусторонний метод аппроксимации

Проведенный анализ дал блестящий пример так называемых двусторонних методов, исследованных В. К. Саульевым

Рассмотрим неявно-явную схему с весами для простейшего уравнения теплопроводности:

(23)

где θ – вес неявной части конечно-разностной схемы,

θ-1 – вес для явной части

Причем . При θ=1 имеем полностью неявную схему, при θ=0 – полностью явную схему, а при θ=1/2 – схему Кранка-Николсона.

В соответствии с гармоническим анализом для схемы (23) получаем неравенство

,

(24)

причем правое неравенство выполнено всегда.

Левое неравенство имеет место для любых значений σ, если . Если же вес θ лежит в пределах , то между σ и θ из левого неравенства устанавливается связь

(25)

являющаяся условием устойчивости неявно-явной схемы с весами (23), когда вес находится в пределах .

Таким образом, неявно-явная схема с весами абсолютно устойчива при и условно устойчива с условием (25) при .

Рассмотрим порядок аппроксимации неявно-явной схемы с весами, для чего разложим в ряд Тейлора в окрестности узла (x j ,t_k) на точном решении значения сеточных функций по переменной t, , по переменной х и полученные разложения подставим в (23):

В этом выражении дифференциальный оператор от квадратной скобки в соответствии с дифференциальным уравнением равен дифференциальному оператору , в соответствии с чем вышеприведенное равенство приобретает вид

После упрощения получаем

,

откуда видно, что для схемы Кранка-Николсона (θ = 1/2) порядок аппроксимации схемы (23) составляет 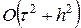, т.е. на один порядок по времени выше, чем для обычных явных или неявных схем. Таким образом, схема Кранка-Николсона при θ = 1/2 абсолютно устойчива и имеет второй порядок аппроксимации по времени и пространственной переменной х.

Используем в уравнение (23) подстановку r=a 2 k /h 2 . Но в то же время его нужно решить для трех «еще не вычисленных» значений , , и . Это возможно, если все значения перенести в левую часть уравнения. Затем упорядочим члены уравнения (23) и в результате получим неявную разностную формулу

(26)

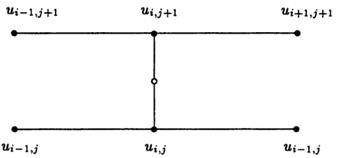
для i=2,3,…,n-1. Члены в правой части формулы (26) известны. Таким образом, формула (26) имеет вид линейной трехдиагональной системы АХ=В. Шесть точек, используемых в формуле Кранка-Николсона (26), вместе с промежуточной точкой решетки, на которой основаны численные приближения, показаны на рисунке 5.

Рисунок 5 – Шаблон (схема) метода Кранка-Николсона

Иногда в формуле (26) используется значение r=1. В этом случае приращение по оси t равно , формула (26) упрощается и принимает вид

, (27)

для i=2,3,…,n-1. Граничные условия используются в первом и последнем уравнениях (т. е. в и соответственно).

Уравнения (27) особенно привлекательны при записи в форме трехдиагональной матрицы АХ = В.

Если метод Кранка-Николсона реализуется на компьютере, то линейную систему АХ = В можно решить либо прямым методом, либо итерационным.

2 Практическая часть

Постановка задачи

Используем метод Кранка-Николсона, чтобы решить уравнение

,

с начальным условием

,

и граничными условиями

Решение в ППП MatLab

Решение будем искать в ППП MatLab 7. Создадим четыре выполняемых m-фала: crnich.m – файл-функция с реализацией метода Кранка-Николсона; trisys.m – файл-функция метода прогонки; f.m – файл-функция задающая начальное условие задачи; fе.m – файл-функция задающая функцию определяющую точное решение задачи(найдена аналитическим путем). Листинги программ представлены в приложении А.

Для простоты возьмем шаг Δх = h = 0,1 и Δt = к = 0,01. Таким образом, соотношение r =1. Пусть решетка имеет n=11 столбцов в ширину и m=11 рядов в высоту.

Анализ результатов

Решения для данных параметров отразим в таблице 1. Трехмерное изображение данных из таблицы покажем на рисунке 5.

Таблица 1 – Значения u(х_i, t_i), полученные методом Кранка-Николсона

Величины, полученные методом Кранка-Николсона, достаточно близки к

аналитическому решению u(x,t) = sin(πx)e -π2 t + sin(3πx)e -9π2 t , истинные значения для последнего представлены в таблице 2

Максимальная погрешность для данных параметров равна 0,005

Таблица 2 – точные значения u(х_i, t_i), при t=0.1

Рисунок 5 –Решение u=u(х_i, t_i), для метода Кранка-Николсона

В зависимости от формы области, краевых условий, коэффициентов исходного уравнения метод конечных разностей имеет погрешности аппроксимации от первого до четвертого порядка относительно шага. В силу этого они успешно используются для разработки программных комплексов автоматизированного проектирования технических объектов.

В МКР строятся, как правило, регулярные сетки, особенности геометрии области учитываются только в около граничных узлах. В связи с этим МКР чаще применяется для анализа задач с прямолинейными границами областей определения функций.

Проблемой методов конечных разностей является высокая размерность результирующей системы алгебраических уравнений (несколько десятков тысяч в реальных задачах. Поэтому реализация методов конечных разностей в составе САПР требует разработки специальных способов хранения матрицы коэффициентов системы и методов решения последней.

1 Березин И.С., Жидков Н.П. Методы вычислений. Т.2. – М.: Физматгиз, 1962.

2 Мэтьюз, Джон, Г., Финк, Куртис, Д. Численные методы. Использование MATLAB, 3-е издание.— М. : Вильяме, 2001. — 720 с

3 Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1972.

4 Формалев В.Ф., Ревизников Д.Л. Численные методы. – М.: ФИЗМАТЛИТ, 2004. — 400 с.

5 Пирумов У.Г. Численные методы. – М.: Издательство МАИ, 1998.

6 Калиткин Н.Н. Численные методы. – М.: Наука, 1976.

Листинг программы для расчета по методу Кранка-Николсона

Видео:Вычислительная математика 19 Устойчивость разностных схемСкачать

Спектральный признак устойчивости Неймана для разностной

ЛЕКЦИЯ 5. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА

МЕТОДОМ КРАНКА – НИКОЛСОН.

Общая постановка разностной задачи уравнений математической

Физики.

Использование разностных схем позволяет свести решение задачи для дифференциального уравнения к решению системы линейных алгебраических уравнений . При этом правые части уравнений, краевые и начальные данные (будем в дальнейшем называть их одним общим термином – входные данные), задаются с определённой погрешностью. В процессе самого численного решения системы также неизбежны ошибки, связанные с округлением. Естественно потребовать от разностной схемы, чтобы малые ошибки, допущенные во входных данных, не нарастали в процессе вычислений и не приводили к искажению решения.

Схемы, которые в процессе счёта усиливают начальные погрешности, называются неустойчивыми и не могут быть использованы на практике.

Пусть имеется непрерывная дифференциальная задача для функции :

, (5.1.1)

где L – дифференциальный оператор, f – правые части (входные данные).

Общая формулировка такой задачи заключается в следующем. Требуется найти функцию u, удовлетворяющую уравнению (5.1.1) во внутренних точках области G, а на участках Г_i границы необходимым граничным условиям, обеспечивающим корректность поставленной задачи.

Применительно к задачам математической физики принято говорить, что задача поставлена корректно, если выполнены два условия:

1) задача однозначно разрешима при любых входных данных из некоторого класса;

2) решение задачи непрерывно зависит от входных данных.

Это требование называют устойчивостью схемы по входным данным или просто устойчивостью.

Для применения разностного метода решения уравнений в частных производных на первом шаге заменяют область непрерывного изменения аргументов (независимых переменных) дискретной областью , где ω_n – внутренняя часть сеточной области, γ_n – её граница. В простейшем случае сеточная область может быть образована совокупностью точек пересечения линий сетки, параллельных осям координат, удалённых друг от друга на расстояния . Они называются шагами сетки по соответствующим направлениям и представляют собой малые параметры. Узлы, лежащие внутри ω_n, образуют совокупность внутренних узлов. Точки пересечений линий сетки с границей Г образуют γ_n – совокупность граничных узлов сеточной области. Разумеется, существует множество других способов построения сеточной области. В общем случае сетка может быть неравномерной, когда шаги h_i по направлениям меняются (h_i ≠ const). В случае криволинейной сетки за шаги сетки принимаются расстояния между соседними узлами, лежащими на одной линии.

При стремлении шагов сетки к нулю сетка сгущается, узлы равномерно покрывают расчётную область G и границу Г. Приближённые решение задачи (5.1.1) отыскиваются в узлах сетки. Совокупность значений приближённого решения в узлах сетки образует сеточную функцию y_n, которая будет отличаться от значений точного решения u_n в одних и тех же узлах.

Разностная задача отличается от исходной задачи (5.1.1) и записывается в виде:

, (5.1.2)

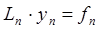
где L_n – конечно-разностный оператор, аппроксимирующий оператор L; y_n – приближённое сеточное решение; f _n – проекция правой части на сеточную область.

Чаще всего задача (5.1.2) – это задача решения достаточно большой системы линейных алгебраических уравнений с разреженными матрицами. Ошибка приближённого решения определяется как разность 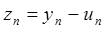, а величина ошибки вычисляется по той или иной норме пространства сеточных функций:

, (5.1.3)

где за норму, например, можно принять максимальное по модулю значение y_n в узлах разностной сетки :

(5.1.4)

Абстрактные формулировки (5.1.1) и (5.1.2) позволяют определить общие, не зависящие от конкретной задачи требования к разностной схеме (5.1.2) , выполнение которых гарантирует малость ошибки приближённого решения.

Главная теорема теории разностных схем даёт ответ на вопрос о близости приближённого и точного решения.

Теорема. Если разностная схема (5.1.2) аппроксимирует (приближает) задачу (5.1.1), т.е. , и решение задачи (5.1.2) устойчиво (непрерывно зависит от входных данных, , где C=const, не зависящая от h), то разностное решение y_n сходится к точному u_n, т.е. . В этих определениях запись h→0 предполагает, что все шаги сетки h_i→0.

Таким образом, мы видим, что если разностная схема устойчива и аппроксимирует исходную задачу, то она сходится (из аппроксимации и устойчивости следует сходимость). Порядок точности и скорость сходимости схемы определяется её порядком аппроксимации.

Спектральный признак устойчивости Неймана для разностной

Задачи Коши.

Пусть дана непрерывная задача (5.1.1) и пусть на сетке её аппроксимирует задача (5.1.2). Будем рассматривать только линейные уравнения в частных производных и аппроксимирующие их линейные разностные схемы. В таком случае определение устойчивости может быть сформулировано следующим образом:

Определение. Разностная схема (5.1.2) устойчива, если для любой функции f_n разностная задача (5.1.2) имеет единственное решение y_n такое что:

(5.2.1)

с константой с, не зависящей от параметра h.

Неравенство (5.2.1) означает, что норма приближённого решения отличается от нормы входных данных на некоторую постоянную величину. Напомним, что в простейшем случае она может быть выражена соотношением (5.1.4).

Рассмотрим один из методов исследования устойчивости разностных схем, который называют методом гармоник или спектральным признаком устойчивости Неймана. Этот метод широко используется в исследовании разностных схем, аппроксимирующих эволюционные уравнения (5.1.4).

Будем рассматривать только задачу Коши и однородные уравнения. Кроме того, коэффициенты уравнений будем считать постоянными, “замораживая” их, даже если они фактически не постоянны в исходной задаче (5.1.1). При таких предположениях разностные уравнения имеют частные решения в виде гармоник произвольной частоты ω:

, (5.2.2)

где c=const; i – мнимая единица; α = ωh; ω – произвольные натуральные числа; λ=λ(α,τ,h) подлежит определению для каждой конкретной системы; (τ – шаг по t; h – шаг по х – в одномерной эволюционной задаче для функции u(x,t)).

После таких предположений входными данными для разностной задачи будут являться только начальные условия.

Условие устойчивости по начальным данным для решений (5.2.2) на основании определения (5.1.1) сводится к требованию ограниченности амплитуды λ этих гармоник:

(5.2.3)

Требуя выполнения неравенства (5.2.3) при произвольном α (т.е. для произвольных гармоник), мы можем найти необходимое условие устойчивости разностной схемы (5.1.2), которое может наложить некоторые ограничения на шаги сетки τ и h. Проверку условия (5.2.3) можно свести к более простому условию:

, (5.2.4)

где А – некоторая константа. Доказательство этого утверждения приведено в [4]. Неравенство (5.2.4) называется спектральным признаком Неймана устойчивости разностных схем.

Изложим широко применяемый на практике способ Неймана исследования разностных задач с начальными данными. Ограничимся случаем разностной задачи Коши с постоянными коэффициентами. Будем исследовать устойчивость по начальным данным. Не умоляя общности рассуждений, исследование проведём на простейшем примере разностной задачи Коши:

(5.2.5)

запишем задачу (5.2.5) в виде:

(5.2.6)

Определим нормы и в линейных нормированных пространствах и равенствами:

(5.2.7)

Тогда условие устойчивости задачи (5.2.6):

(5.2.8)

в терминах (5.2.7) примет вид:

, (5.2.9)

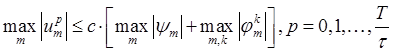
где c=const не зависит от h (и от τ=rh, r=const). Условие (5.2.9) должно выполнятся при произвольных и .

В частности, для устойчивости необходимо, чтобы оно выполнялось при произвольных и , т.е. чтобы решение задачи

(5.2.10)

(5.2.11)

при произвольной ограниченной функции .

Свойство (5.2.11), необходимое для устойчивости (5.2.9) задачи (5.2.5), называется устойчивостью задачи (5.2.5) относительно возмущения начальных данных. Оно означает, что возмущение , внесённое в начальные данные задачи (5.2.5), вызовет возмущение решения задачи (5.2.5), которое в силу (5.2.10) не более чем в “с” раз превосходит возмущение начальных данных, причём “с” не зависит от h.

Для условия устойчивости задачи Коши (5.2.5) по начальным данным необходимо, чтобы условие (5.2.11) выполнялось, в частности, если есть какая-нибудь гармоника

(5.2.12)

где α – вещественный параметр, а — мнимая единица. Но решение задачи (5.2.10) при начальном условии (5.2.12) имеет вид:

(5.2.13)

где определяется путём подстановки выражения (5.2.13) в однородное разностное уравнение задачи (5.2.10):

(5.2.14)

Для решения (5.2.13) справедливо равенство:

Тогда для выполнения условия (5.2.11) необходимо, чтобы при всех вещественных α выполнялось неравенство:

(5.2.15)

(5.2.16)

где c₁ – некоторая постоянная, не зависящая от α и τ. Условия (5.2.15) и (5.2.16) — необходимое спектральное условие Неймана для рассматриваемого нами примера. Спектральным оно называется по следующей причине.

Существование решения вида (5.2.13) показывает, что гармоника является собственной функцией оператора перехода

, (5.2.17)

который в силу разностного уравнения (5.2.10) ставит в соответствие сеточной функции , определённой на слое t=t_p, сеточную функцию , определённую на слое t=t_p+1. Число является соответствующим этой гармонике собственным числом оператора перехода. Линия, которую пробегает точка на комплексной плоскости, когда α пробегает вещественную ось, вся состоит из собственных значений и является спектром оператора перехода.

Таким образом, необходимое условие устойчивости (5.2.16) можно сформулировать так: спектр оператора перехода, соответствующего разностному уравнению задачи (5.2.10), должен лежать в круге радиуса на комплексной плоскости. В нашем примере спектр (5.2.14) не зависит от шага τ. Поэтому условие (5.2.16) равносильно требованию, чтобы спектр лежал в единичном круге:

(5.2.18)

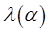
Воспользуемся сформулированным признаком для анализа устойчивости задачи (5.2.5). Спектр (5.2.14) представляет собой окружность с центром в точке и радиусом к на комплексной плоскости.

В случае эта окружность лежит внутри единичного круга (касаясь его в точке λ=1), при r=1 совпадает с единичной окружностью, а при лежит вне единичного круга .

Соответственно необходимое условие устойчивости (5.2.18) выполнено при и не выполнено .

В общем случае задачи Коши для разностных уравнений и систем разностных уравнений необходимый спектральный признак устойчивости Неймана состоит в том, что спектр разностной задачи при всех достаточно малых h должен лежать в круге

(5.2.19)

на комплексной плоскости, как бы мало ни было заранее выбранное положительное число ε .

Заметим, что если для разностной задачи спектр окажется не зависящим от h (и от τ), то условие (5.2.19) равносильно требованию, чтобы спектр лежал в единичном круге (3.19).

Под спектром разностной задачи в условии (5.2.19) понимается совокупность всех , при которых соответствующее однородное разностное уравнение (или система уравнений) имеет решение вида

, (5.2.20)

где u 0 – число (единица), если речь идёт о скалярном разностном уравнении, и числовой вектор, если речь идёт о векторном разностном уравнении, т.е. о системе скалярных разностных уравнений.

Если необходимое условие Неймана (5.2.19) не выполнено, то ни при каком разумном выборе норм нельзя ожидать устойчивости, а в случае его выполнения можно надеяться, что при некотором разумном выборе норм устойчивость имеет место.

Рассмотренный выше необходимый признак устойчивости Неймана для исследования разностной задачи Коши с постоянными коэффициентами, можно применять и в случае разностной задачи Коши с непрерывными, но не постоянными коэффициентами, а также для задач в ограниченных областях, когда граничные условия задаются не только при t=0, но и на боковых границах. Также этим признаком можно пользоваться и для исследования нелинейных задач.

🔥 Видео

Разностные схемы для решения уравнения переноса. Numerical Schemes for Linear Advection Equation.Скачать

27. Уравнения переносаСкачать

Методы математической физики. Сеточный метод. Неявная схема. Устойчивость и сходимость. Фролова Е.В.Скачать

Пример построения схем для уравнения переноса в пространстве неопределенных коэффициентов.Скачать

Кобельков Г. М. - Численные методы. Часть 2. Семинары - Лекция 4Скачать

Вычислительная математика 17 Теория разностных схемСкачать

Кобельков Г. М. - Численные методы. Часть 2 - Решение уравнений в частных производныхСкачать

Лукьяненко Д. В. - Численные методы - Лекция 18Скачать

Кобельков Г. М. - Численные методы. Часть 2. Семинары - Лекция 3Скачать

Кобельков Г. М. - Численные методы. Часть 2. Семинары - Лекция 2Скачать

Кобельков Г. М. - Численные методы. Часть 2. Семинары - Лекция 6Скачать

Математика в неожиданных местах: Разностная схема для уравнения теплопроводностиСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Лекция №1.4 Схема с весами, схема Кранка НикольсонСкачать

Решение задачи теплопроводности (Явная разностная схема)Скачать

6-2. Метод сетокСкачать

Схемы в пространстве неопределенных коэффициентов. Schemes in the Space of Indefinite Coefficients.Скачать

Методы вычислений, 17131, Семинар 23.04, Черный С.Г.Скачать