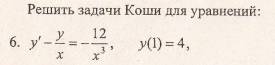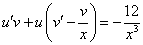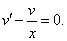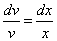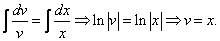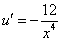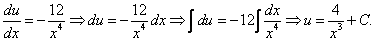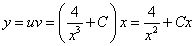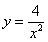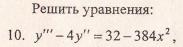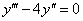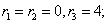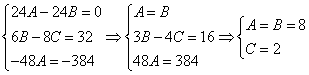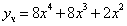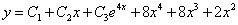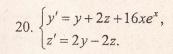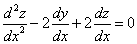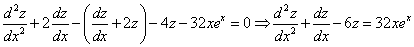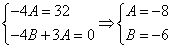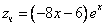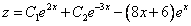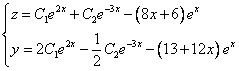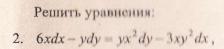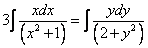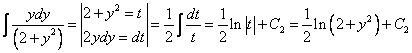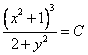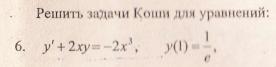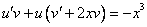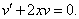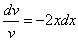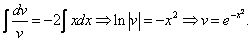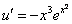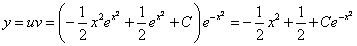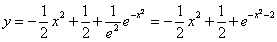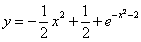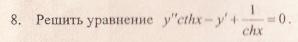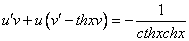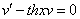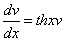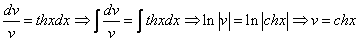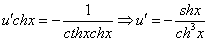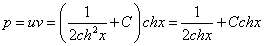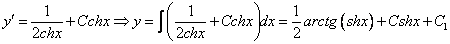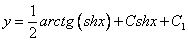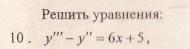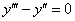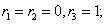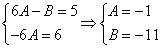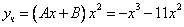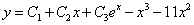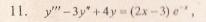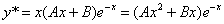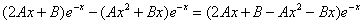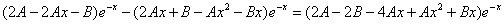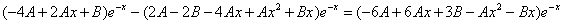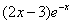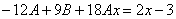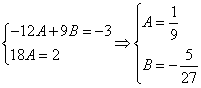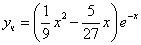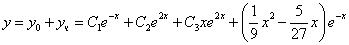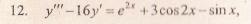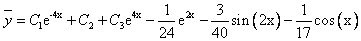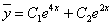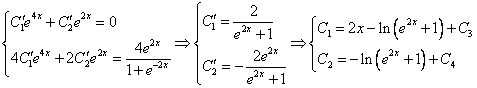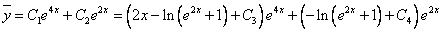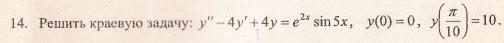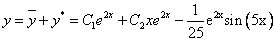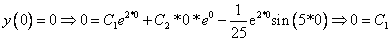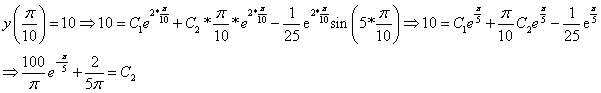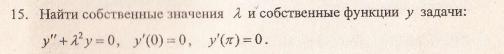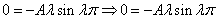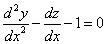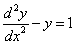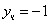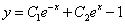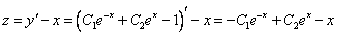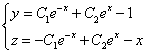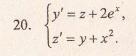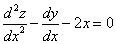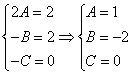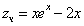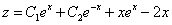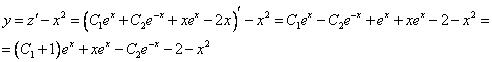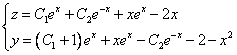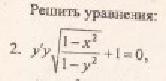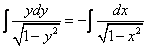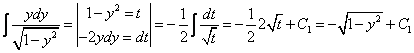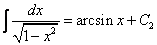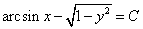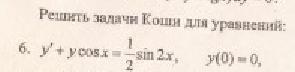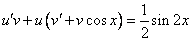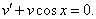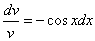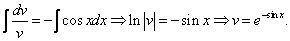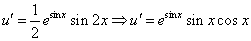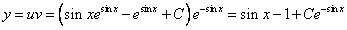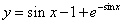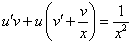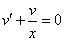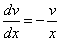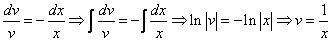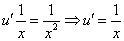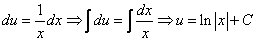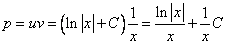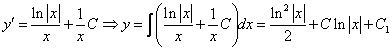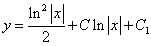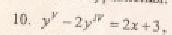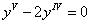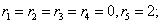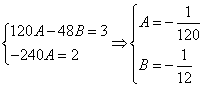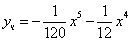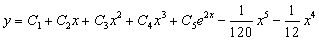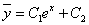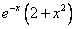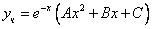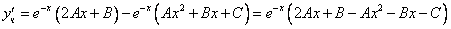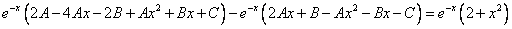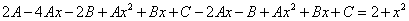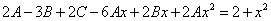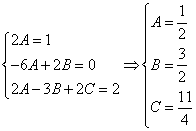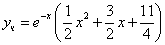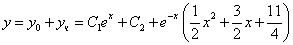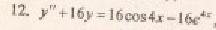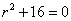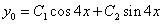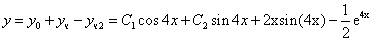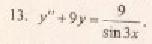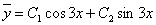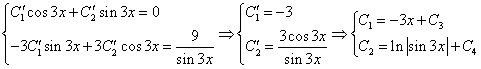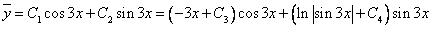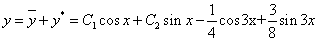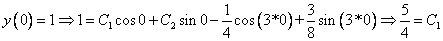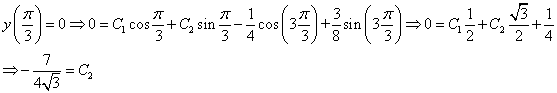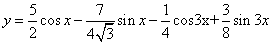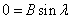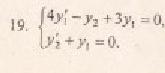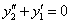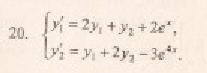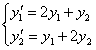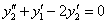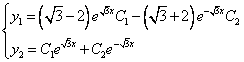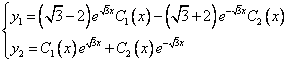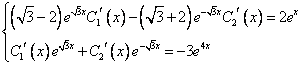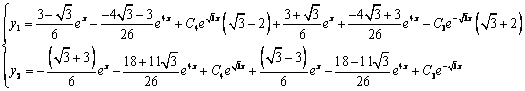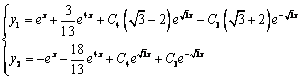материал для подготовки к егэ (гиа) на тему
Видео:Контрольная работа Дифференциальные уравнения Задача1Скачать

Скачать:
| Вложение | Размер |
|---|---|
| Контрольная работа «Решение дифференциальных уравнений» | 49 КБ |
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Предварительный просмотр:
Контрольная работа №1 «Решение дифференциальных уравнений»
Пример 1. Решить дифференциальное уравнение и найти частное решение, удовлетворяющее начальному условию у (0) = 1.
Интегрируем обе части последнего равенства
В результате получим
Таким образом, получаем общий интеграл
Находим частное решение уравнения. Подставляем начальное условие
Отсюда получаем частный интеграл
1. Являются ли данные функции решениями данных дифференциальных уравнений.
1 .
2. Найти общее и частное решение дифференциального уравнения, удовлетворяющее начальным условием при
1.Являются ли данные функции решениями данных дифференциальных уравнений
2. Найти общее и частное решение дифференциального уравнения, удовлетворяющее начальным условием при
Контрольная работа №1 «Решение дифференциальных уравнений»
Пример 1. Решить дифференциальное уравнение и найти частное решение, удовлетворяющее начальному условию у (0) = 1.
Интегрируем обе части последнего равенства
В результате получим
Таким образом, получаем общий интеграл
Находим частное решение уравнения. Подставляем начальное условие
Отсюда получаем частный интеграл
1. Являются ли данные функции решениями данных дифференциальных уравнений.
1 .
2. Найти общее и частное решение дифференциального уравнения, удовлетворяющее начальным условием при
1.Являются ли данные функции решениями данных дифференциальных уравнений
2. Найти общее и частное решение дифференциального уравнения, удовлетворяющее начальным условием при
Видео:Контрольная по диффурам за 20 минут!Скачать

По теме: методические разработки, презентации и конспекты
Методическая разработка занятия по предмету Элементы высшей математики по теме: «Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными».
Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными.Тип занятия: комбинированный, с элементами игры.Формы занятия: индивидуальная, группо.
Решение дифференциальных уравнений с разделяющимися переменными
Решение дифференциальных уравнений с разделяющимися переменными.
Решение дифференциальных уравнений с разделяющимися переменными. Методическая разработка.
Решение дифференциальных уравнений с разделяющимися переменными. Методическая разработка.
Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка.
Презентация к занятию по дисциплине ЕН.02 Математика по теме «Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка».
Контрольная работа Решение показательных и логарифмических уравнений
Контроль умений учащихся решать уравнения и неравенства.
Контрольная работа по теме: «Уравнения и неравенства с двумя переменными» 9 класс
Контрольная работа по теме: «Уравнения и неравенства с двумя переменными»1. Решить систему уравнений способом сложения.2. Решить систему уравнений способом подстановки.3. Найти периме.
Контрольная работа по теме: «Уравнения и неравенства с двумя переменными» 9 класс
Контрольная работа №4 по теме: «Уравнения и неравенства с двумя переменными»Вариант 1Контрольная работа №4 по теме: «Уравнения и неравенства с двумя переменными» .
Видео:2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Контрольная работа по теме «Дифференциальные уравнения»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Контрольная работа по теме «Дифференциальные уравнения»
1. Найти частные решения дифференциальных уравнений с разделяющимися переменными:
а) 





2. Найти частные решения однородных дифференциальных уравнений второго порядка:
а) 





в) 


3. Найти частное решение неоднородного дифференциального уравнения второго порядка:
а) 





1. Найти частные решения дифференциальных уравнений с разделяющимися переменными:
а) 





2. Найти частные решения однородных дифференциальных уравнений второго порядка:
а) 





в) 


3. Найти частные решения неоднородных дифференциальных уравнений второго порядка:
а) 





Видео:Контрольная работа. Уравнения с МОДУЛЕМСкачать

Дифференциальные уравнения (варианты)
Это уравнение вида 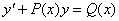


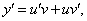
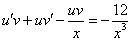
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 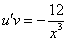
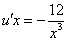
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Используем условие 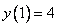

Ответ:
Решим соответствующее однородное уравнение
Составим характеристическое уравнение 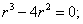
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид 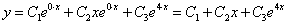
Частное решение неоднородного уравнения будем искать в виде 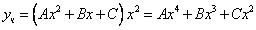
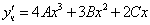
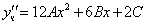
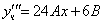
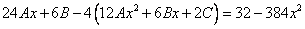
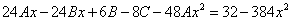
Тогда частное решение
Общее решение неоднородного примет вид:
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 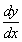
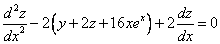
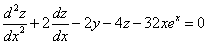
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение 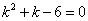
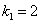
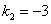
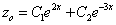
Частное решение неоднородного уравнения будем искать в виде 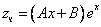

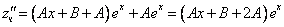
Подставим в исходное 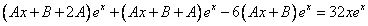
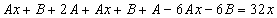
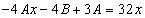
Тогда частное решение
Общее решение неоднородного примет вид:
Из второго уравнения
Ответ:
Видео:Математика это не ИсламСкачать

Вариант 2
Данное уравнение – уравнение с разделяющимися переменными. Разделим переменные: 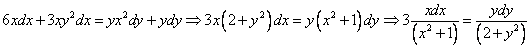
Посчитаем интегралы отдельно:
Тогда: 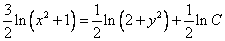
Ответ:
Это уравнение вида 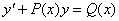


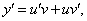
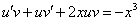
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 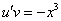
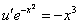
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
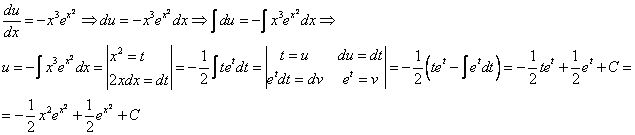
Используем условие 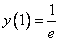
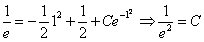
Ответ:
Данное уравнение не содержит у, следовательно понизить его порядок можно с помощью подстановки 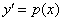
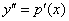
Отсюда 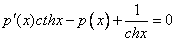
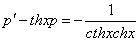
Замена 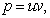
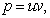
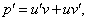
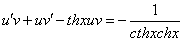
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 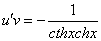
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Ответ:
Решим соответствующее однородное уравнение
Составим характеристическое уравнение 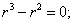
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид 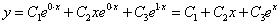
Частное решение неоднородного уравнения будем искать в виде 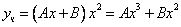

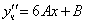
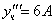
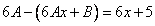
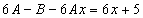
Тогда частное решение
Общее решение неоднородного примет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r3-3r2+4= 0
Корни характеристического уравнения:
R1 = -1 и корень характеристического уравнения r2 = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции: y1 = e-x, y2 = e2x, y3 = xe2x
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = (2•x-3)•e-x
Уравнение имеет частное решение вида:
Y’ =
Y» =
Y»’ =
которые подставляем в исходное дифференциальное уравнение:
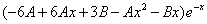
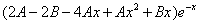
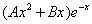
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Частное решение имеет вид:
Таким образом, общее решение дифференциального уравнения имеет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r3 — 16r = 0
Корни характеристического уравнения:r1 = -4, r2 = 0, r3 = 4
Следовательно, фундаментальную систему решений составляют функции:
Y1 = e-4x, y2 = e0x, y3 = e4x
Общее решение однородного уравнения имеет вид:
Правая часть F(x) = e2•x+3cos2x-sinx
Будем искать отдельно частные решения для F1(x) = e2•x, F2(x) = 3cos2x, F3(x) = — sinx
Рассмотрим правую часть: F1(x) = e2•x
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 1, Q(x) = 0, α = 2, β = 0.
Следовательно, число α + βi = 2 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (8•A•e2x) -16(2•A•e2x) = e2•x или -24•A•e2x = e2•x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = -1/24;
Частное решение имеет вид: y* = -1/24e2x
Рассмотрим правую часть: F2(x) = 3•cos(2•x)
Поиск частного решения.
Уравнение имеет частное решение вида:y* = Acos(2x) + Bsin(2x)
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (8•A•sin(2x)-8•B•cos(2x)) -16(2•B•cos(2x)-2•A•sin(2x)) = 3•cos(2•x)
или 40•A•sin(2x)-40•B•cos(2x) = 3•cos(2•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 0;B =-3/40;
Частное решение имеет вид:
Поиск частного решения.
Уравнение имеет частное решение вида: y* = Acos(x) + Bsin(x)
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (A•sin(x)-B•cos(x)) -16(B•cos(x)-A•sin(x)) = — sin(x)
или 17•A•sin(x)-17•B•cos(x) = — sin(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = -1/17;B = 0;
Частное решение имеет вид: y* = -1/17cos(x) + 0sin(x) или y* = -1/17cos(x)
Окончательно, общее решение данного уравнения
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 -6 r + 8 = 0
Корни характеристического уравнения: r1 = 2, r2 = 4
Следовательно, фундаментальную систему решений составляют функции: y1 = e4x, y2 = e2x
Общее решение однородного уравнения имеет вид:
Для поиска частного решения воспользуемся методом вариации произвольных постоянных. Для этого решим систему:
Тогда окончательно
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 -4 r + 4 = 0
Корни характеристического уравнения:
Корень характеристического уравнения r1 = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции: y1 = e2x, y2 = xe2x
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = e2•x•sin(5•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 1, Q(x) = 0, α = 2, β = 5.
Следовательно, число α + βi = 2 + 5i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y* = e2x(Acos(5x) + Bsin(5x))
Которые подставляем в исходное дифференциальное уравнение:
Y» -4y’ + 4y = (-e2x((20•A+21•B)•sin(5x)+(21•A-20•B)•cos(5x))) -4(e2x((2•B-5•A)•sin(5x)+(2•A+5•B)•cos(5x))) + 4(e2x(Acos(5x) + Bsin(5x))) = e2•x•sin(5•x)
или -25•A•e2x•cos(5x)-25•B•e2x•sin(5x) = e2•x•sin(5•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 0;B = -1/25;
Частное решение имеет вид: y* = e2x(0cos(5x) -1/25sin(5x)) илиy* =-1/25 e2x sin(5x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Используем начальные условия
Тогда окончательно,
Характеристическое уравнение исходного дифференциального уравнения 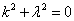
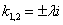
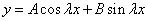
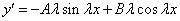
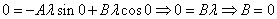
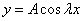
Подставляем во второе граничное условие
При А=0 и В=0 – тривиальное решение у=0
Поэтому 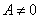
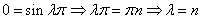
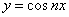
Метод исключения неизвестных.
Продифференцируем по х первое уравнение
Исключая с помощью второго уравнения 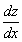
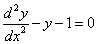
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение 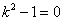
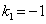
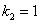
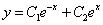
Частное решение неоднородного уравнения будем искать в виде 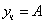
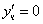
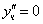
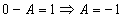
Тогда частное решение
Общее решение неоднородного примет вид:
Из первого уравнения
Ответ:
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 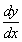
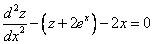
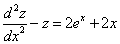
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение 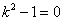
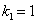
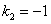
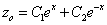
Частное решение неоднородного уравнения будем искать в виде 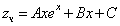
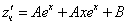
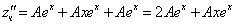
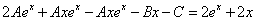
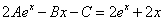
Тогда частное решение
Общее решение неоднородного примет вид:
Из второго уравнения
Ответ:
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Вариант 5
Данное уравнение – уравнение с разделяющимися переменными. Разделим переменные: 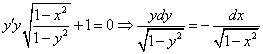
Посчитаем интегралы отдельно:
Тогда: 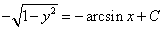
Ответ:
Это уравнение вида 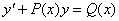


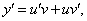
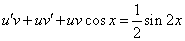
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Интегрируя, находим
Подставим найденную функцию v во второе уравнение 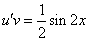
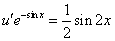
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Используем условие 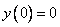
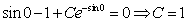
Ответ:
Данное уравнение не содержит у, следовательно понизить его порядок можно с помощью подстановки 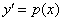
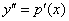
Отсюда 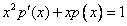
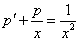
Замена 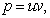
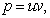
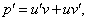
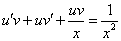
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 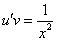
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Ответ:
Решим соответствующее однородное уравнение
Составим характеристическое уравнение 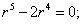
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид
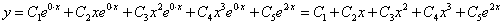
Частное решение неоднородного уравнения будем искать в виде 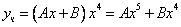
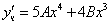
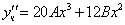
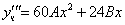
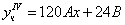
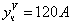
Подставим в исходное 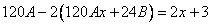
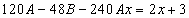
Тогда частное решение
Общее решение неоднородного примет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 — r= 0
Вынесем r за скобку. Получим: r(r-1) = 0
Корни характеристического уравнения:r1 = 0, r2 = 1
Следовательно, фундаментальную систему решений составляют функции: y1 = e0x, y2 = ex.
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) =
Уравнение имеет частное решение вида:
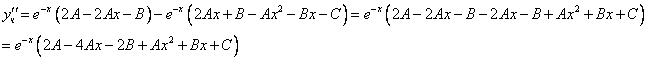
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Частное решение имеет вид:
Таким образом, общее решение дифференциального уравнения имеет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
Корни характеристического уравнения:(комплексные корни): r1 = 4i, 
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = 16•cos(4•x)-16•e4x, будем искать отдельно частные решения для f1(x)= 16•cos(4•x) и для f2(x)= 16•e4x
Для f1(x) = 16•cos(4•x) имеем
Уравнение имеет частное решение вида: y ч1* = x (Acos(4x) + Bsin(4x))
Которые подставляем в исходное дифференциальное уравнение:
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 0;B = 2;
Частное решение имеет вид: yч1* = x (0cos(4x) + 2sin(4x)) или y ч1* = 2xsin(4x)
Частное решение ищем в виде y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 16, Q(x) = 0, α = 4, β = 0.
Следовательно, число α + βi = 4 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
Которые подставляем в исходное дифференциальное уравнение:
Y» + 16y = (16•A•e4x) + 16(Ae4x) = 16•e4•x или 32•A•e4x = 16•e4•x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 1/2;
Частное решение имеет вид: y*ч2 = 1/2e4x
Таким образом, общее решение дифференциального уравнения имеет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 + 9 = 0
Корни характеристического уравнения: r1 = -3i, r2 = 3i
Общее решение однородного уравнения имеет вид:
Для поиска частного решения воспользуемся методом вариации произвольных постоянных. Для этого решим систему:
Тогда окончательно
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 + 1 = 0
Корни характеристического уравнения:(комплексные корни): r1 = i,
Следовательно, фундаментальную систему решений составляют функции:
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = 2•cos(3•x)-3•sin(3•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 2, Q(x) = -3, α = 0, β = 3.
Следовательно, число α + βi = 0 + 3i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y* = Acos(3x) + Bsin(3x)
Которые подставляем в исходное дифференциальное уравнение:
Y» + y = (-9(A•cos(3x)+B•sin(3x))) + (Acos(3x) + Bsin(3x)) = 2•cos(3•x)-3•sin(3•x)
или -8•A•cos(3x)-8•B•sin(3x) = 2•cos(3•x)-3•sin(3•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = -1/4;B = 3/8;
Частное решение имеет вид: y* = -1/4cos(3x) + 3/8sin(3x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Используем начальные условия
Тогда окончательно,
Характеристическое уравнение исходного дифференциального уравнения 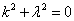
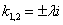
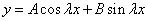
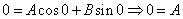
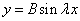
Подставляем во второе граничное условие
При А=0 и В=0 – тривиальное решение у=0
Поэтому 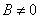
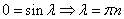
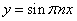
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 
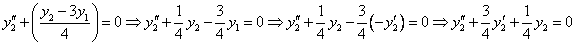
Таким образом, задача свелась к линейному однородному уравнению с постоянными коэффициентами второго порядка. Характеристическое уравнение 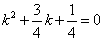
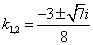
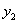
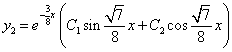
Из второго уравнения
Ответ:
Найдём сначала общее решение соответствующей однородной системы
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 
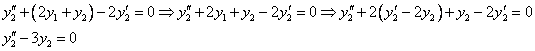
Таким образом, задача свелась к линейному однородному уравнению с постоянными коэффициентами второго порядка. Характеристическое уравнение 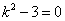
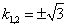
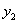
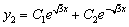
Из второго уравнения 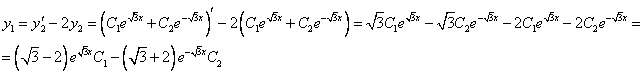
Принимаем частное решение первоначальной системы в виде:
Решаем данную систему по формулам Крамера, получим два дифференциальных уравнения первого порядка:
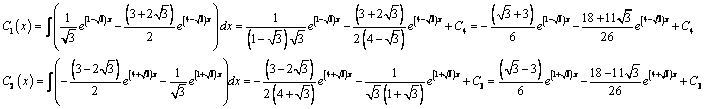
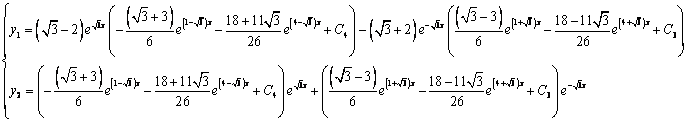
Ответ:
🎥 Видео
1. Что такое дифференциальное уравнение?Скачать

Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать
1. Дифференциальные уравнения высших порядков. Демонстрационный вариант контроля по модулюСкачать

Дифференциальные уравнения. 11 класс.Скачать

Математика Высшая Решение задач Контрольных работ Помощь на экзаменах онлайн ЕГЭ ГИА РепетиторСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

11. Уравнения в полных дифференциалахСкачать

Лабораторная работа 1. Решение систем обыкновенных дифференциальных уравненийСкачать