Каноническое уравнение поверхности онлайн калькулятор

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Нахождение уравнений прямой, заданной пересечением двух плоскостей

Этот онлайн калькулятор находит уравнения прямой, заданной пересечением двух плоскостей в пространстве.

Этот онлайн калькулятор предназначен для проверки решений задач, которые можно сформулировать следующим образом:

Записать канонические уравнения прямой, заданной уравнениями двух плоскостей

Вы задаете коэффициенты уравнений плоскостей, калькулятор выдает уравнения прямой в канонической форме. Немного теории, как обычно, можно почерпнуть под калькулятором

Нахождение уравнений прямой, заданной пересечением двух плоскостей

Канонические уравнения прямой, заданной пересечением двух плоскостей

Если плоскости пересекаются, то система уравнений, приведенная в начале статьи, задает прямую в пространстве. Для записи уравнений этой прямой в каноническом виде, надо найти какую либо точку, принадлежащую этой прямой, и направляющий вектор.

Точка, принадлежащая прямой, также принадлежит и каждой из плоскостей, то есть является одним из решений системы уравнений выше. Для нахождения точки, принадлежащей прямой, переходят от системы из двух уравнений с тремя неизвестными к системе из двух уравнений с двумя неизвестными, произвольно принимая какую-либо координату точки за ноль. Как правило, при решении задач, выбирают ту координату, при занулении которой решение системы из двух уравнений с двумя неизвестными дает в ответе целые числа. Калькулятор учитывает этот факт и также пытается найти целочисленное решение, зануляя все координаты по очереди.

Направляющий вектор прямой ортогонален нормальным векторам плоскостей, которые задаются коэффициентами A, B и С в общем уравнении плоскости . Таким образом его можно найти как результат векторного произведения нормальных векторов плоскостей .

Точка и вектор дают нам канонические уравнения прямой:

Существуют частные случаи, когда одна или две координаты направляющего вектора равны нулю.

В случае, если нулю равны две координаты, направляющий вектор коллинеарен одной из координатных осей. Соответственно, точки прямой могут принимать любое значение по этой оси, при этом значения по двум другим осям будут постоянны. Например, если двумя нулевыми координатами будут y и z, канонические уравнения прямой будут выглядеть так:

В случае. если нулю равна одна координата, направляющий вектор лежит в одной из координатных плоскостей (плоскостей, образованных парами координатных осей), значение координаты по третьей оси, ортогональной этой плоскости (как раз той, для которой координата направляющего вектора равна нулю), опять будет постоянным. Например, если нулевой координатой будет x, то канонические уравнения прямой будут выглядеть так:

Эти случаи также учитываются калькулятором.

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Приведение кривой второго порядка к каноническому виду

Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.

Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.

Видео:Каноническое уравнение прямой в пространстве. 11 класс.Скачать

Алгоритм перехода кривой второго порядка к каноническому виду

Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0

Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 — 4x) = 2(y+3/2) 2
-(x 2 — 4x + 4) = (y+3/2) 2
-(x — 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x — 2) 2 = 0

Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0

Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Видео:Видеоурок "Гипербола"Скачать

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Ввод данных в калькулятор для составления уравнения плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления уравнения плоскости

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Уравнение плоскости.

Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки

В зависимости от условий задачи уравнение плоскости можно составить следующими способами:

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле

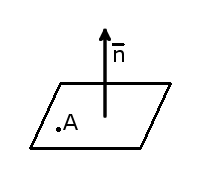
Если заданы координаты точки A( x ₁, y ₁, z ₁) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

🔍 Видео

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Каноническое уравнение окружностиСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Поверхности второго порядкаСкачать

53. Приведение общего уравнения кривой к каноническому видуСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Олегу Тинькову запрещён вход на Мехмат МГУСкачать

2. Приведение уравнений второго порядка к каноническому видуСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

Приводим уравнение кривой 2 порядка к каноническому видуСкачать

§21 Каноническое уравнение гиперболыСкачать