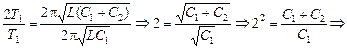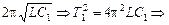| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
3)
4) Знак 
17. [Уд1] (ВО1) Направления индукционного тока в контуре и магнитного поля (к нам) указывают, что для величины магнитной индукции справедливо соотношение
1)
2)
3)
4) Знак 
18. [Уд1] (О) При движении рамок в однородном магнитном поле в направлениях, указанных стрелками, ЭДС индукции возникает в случае под номером
19. [Уд1] (О) По параллельным металлическим проводникам, расположенным в однородном магнитном поле, с постоянной скоростью перемещается перемычка. Зависимость Ei — ЭДС индукции, возникающей в цепи, правильно представлена на рисунке под номером
Тема: 250 Электромагнитные колебания и волны
V251П Электромагнитные колебания.
S251 П электромагнитные колебания – 23 задания
1. [Уд] (ВО1) В колебательном контуре зависимость заряда на пластинах конденсатора от времени описывается дифференциальным уравнением вида 
2. [Уд] (ВО1) В колебательном контуре зависимость заряда на пластинах конденсатора от времени описывается дифференциальным уравнением вида 
3. [Уд] (ВО1) В колебательном контуре зависимость заряда на пластинах конденсатора от времени описывается дифференциальным уравнением вида 
4. [Уд] (ВО1). Если частота колебаний в контуре возросла в 3 раза, а заряд конденсатора и индуктивность катушки не менялись, то энергия магнитного поля в катушке … раз(а).
1) уменьшилась в 3
2) увеличилась в 3
3) уменьшилась в 9
4) увеличилась в 9
5. [Уд] (ВО1) Максимальная энергия электрического колебательного контура 4,5 Дж. При циклической частоте свободных колебаний в контуре, равной 1·104с-1, и емкости конденсатора 4 мкФ максимальный ток через катушку индуктивности равен
6. [Уд] (ВО1) В колебательном контуре в начальный момент времени напряжение на конденсаторе максимально. Напряжение на конденсаторе станет равным нулю через долю периода 
1)
2)
3)
7. [Уд] (ВО1) В колебательном контуре в начальный момент времени напряжение на конденсаторе максимально. Сила тока станет равной нулю через долю периода 
1)
2)
3)
8. [Уд] (ВО1) Сила тока в колебательном контуре изменяется по закону 
9. [Уд] (ВО1) Если в колебательном контуре увеличить емкость конденсатора в 2 раза и заряд на нем увеличить в 2 раза, то амплитуда колебаний тока в контуре … раз(а).
1) увеличится в 2
2) увеличится в
3) уменьшится в
4) уменьшится в 2
10. [Уд] (ВО1) Если в колебательном контуре уменьшить емкость конденсатора в 2 раза, то, при одинаковом заряде конденсатора, максимальная энергия магнитного поля в катушке индуктивности … раза.
1) увеличится в 2
2) увеличится в
3) уменьшится в
4) уменьшится в 2
11. [Уд] (ВО1) Если частота колебаний в контуре возросла в 2 раза, а заряд конденсатора и индуктивность катушки не менялись, то энергия магнитного поля в катушке … раза.
1) уменьшилась в 2
2) увеличилась в 2
3) уменьшилась в 4
4) увеличилась в 4
12. [Уд] (ВО1) Время релаксации затухающих электромагнитных колебаний наибольшее в случае
1) 
2) 
3) 
4) 
13. [Уд] (ВО1) Ниже приведены уравнения затухающих электромагнитных колебаний. Логарифмический декремент затухания наибольший в случае
1) 
2)
3) 
4) 
14. [Уд] (ВО1) Уменьшение амплитуды колебаний в системе с затуханием характеризуется временем релаксации. Если при неизменном омическом сопротивлении в колебательном контуре увеличить в 2 раза индуктивность катушки, то время релаксации … раза.
1) уменьшится в 4
2) увеличится в 2
3) увеличится в 4
4) уменьшится в 2
15. [Уд] (ВО1) Уменьшение амплитуды колебаний в системе с затуханием характеризуется временем релаксации. Если при неизменной индуктивности в колебательном контуре увеличить омическое сопротивление в 2 раза катушки, то время релаксации … раза.
1) уменьшится в 4
2) увеличится в 2
3) увеличится в 4
4) уменьшится в 2
16. [Уд] (ВО1) Ниже приведены уравнения собственных незатухающих электромагнитных колебаний в четырех контурах с одинаковой емкостью. Индуктивность L контура наименьшая в случае
1) q = 10-6cos(4πt +
3) q = 10-8cos(πt +
17. [Уд] (ВО1) Ниже приведены уравнения собственных незатухающих электромагнитных колебаний в четырех контурах с одинаковой индуктивностью. Емкость C контура наибольшая в случае
1) q = 10-6cos(4πt +
3) q = 10-8cos(πt +
18. [Уд] (ВО1) Уравнение изменения тока со временем в колебательном контуре имеет вид 
19. [Уд] (ВО1) Уравнение изменения тока со временем в колебательном контуре имеет вид 
20. [Уд] (ВО1) Уравнение изменения тока со временем в колебательном контуре имеет вид 

Видео:Графические зависимости заряда и силы тока от времени в идеальном колебательном контуре. 11 класс.Скачать

Уравнение колебаний
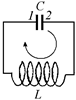 Рис. 15.4 Рис. 15.4 |
Попробуем выяснить, как зависят от времени заряд на обкладке конденсатора и сила тока в колебательном контуре (рис. 15.4). Но прежде, чем мы приступим к вычислениям, отметим следующее:
1) ток в процессе колебаний течет то в одном, то в другом направлении. Чтобы величина силы тока в данный момент времени была определена однозначно, необходимо задать направление обхода контура. Тогда ток, текущий вдоль направления обхода, считаем положительным, а против – отрицательным;
2) заряды на пластинах конденсатора всегда равны по величине и противоположны по знаку, поэтому надо договориться, заряд какой пластины (1 или 2) в данный момент мы рассматриваем;
3) напряжение между пластинами конденсатора – это разность между потенциалами пластин. Эта величина, как и сила тока, меняет знак в процессе колебаний. Чтобы величина была однозначно определена в данный момент времени, договоримся, что мы считаем напряжением U = j1 – j2 или U = j2 – j1, где j1 и j2 – потенциалы пластин 1 и 2 соответственно.
С учетом данных замечаний приступим к установлению зависимости от времени заряда q(t), тока i(t) и напряжения и(t):
1) зададим направление обхода контура по часовой стрелке (см. рис. 15.4);
2) назовем «первой» ту пластинку конденсатора, которая встретилась первой после катушки при следовании по направлению обхода контура, а «второй» – смежную с ней пластину. Зарядом конденсатора будем называть заряд первой пластины;
3) под напряжением будем понимать величину U = j1 – j2. Если q1 > 0, а q2 = –q1 0. Но величина Dq может быть и отрицательной, если ток в данный момент времени t течет против направления обхода, тогда i(t)

СТОП! Решите самостоятельно: В1–В3, С1–С2.
Задача 15.1. В каких пределах должна изменяться индуктивность катушки колебательного контура, чтобы в контуре происходили колебания с частотой от f1 = 400 Гц до f2 = 500 Гц. Емкость конденсатора С = 10 мкФ.
| f1 = 400 Гц f2 = 500 Гц С = 10 мкФ | Решение. Воспользуемся формулой (15.9): 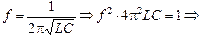 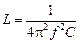 , отсюда , отсюда 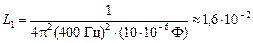 Гн; Гн; |
| L1 = ? L2 = ? |
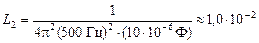
Ответ: индуктивность должна изменяться от 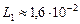
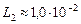
СТОП! Решите самостоятельно: А1–А4.
Задача 15.2. Период электрических колебаний в контуре 1,0×10 –5 с. При подключении параллельно конденсатору контура дополнительного конденсатора электроемкостью 3,0×10 –8 Ф период колебаний увеличился в два раза. Определите индуктивность катушки и начальную электроемкость конденсатора колебательного контура.
| Т1 = 1,0×10 –5 с С2 = 3,0×10 –8 Ф Т2/Т1 = 2 | Решение. Вспомним, что при параллельном соединении емкости конденсаторов складываются, и применим формулу Томсона для обоих случаев: Т1 =  , (1) 2Т1 = , (1) 2Т1 = 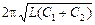 , (2) , (2) |
| L = ? C1 = ? |
Разделим (2) на (1) и получим
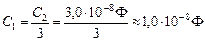
Выразим индуктивность L из (1):
Т1 =
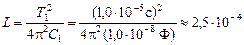
Ответ: 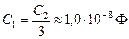
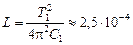
СТОП! Решите самостоятельно: В4–В6, С3–С5.
Задача 15.3. Колебательный контур состоит из катушки индуктивностью L = 0,20 Гн и конденсатора емкостью С = 1,0×10 –5 Ф. Конденсатор зарядили до напряжения U = 2,0 В, и он начал разряжаться. Каким будет ток в момент, когда энергия контура окажется поровну распределенной между электрическим и магнитным полем?
| L = 0,20 Гн С = 1,0×10 –5 Ф U = 2,0 В Wм = Wэ | Решение. Энергия контура равна 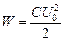 . В тот момент, когда энергии электрического и магнитного полей равны, на долю энергии магнитного поля приходится ровно половина полной энергии контура, поэтому . В тот момент, когда энергии электрического и магнитного полей равны, на долю энергии магнитного поля приходится ровно половина полной энергии контура, поэтому |
| i = ? |
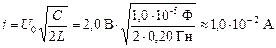
Ответ: 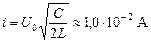
СТОП! Решите самостоятельно: А5–А7, В7–В9.
Задача 15.4.Заряд q на пластинах конденсатора колебательного контура изменяется с течением времени t по закону q = =10 -6 cosl0 4 pt. Записать закон зависимости силы тока от времени i(t). Найти период и частоту колебаний в контуре, амплитуду колебаний заряда и амплитуду колебаний силы тока. Все величины считать точными и заданными в единицах СИ.
| q = 10 -6 cosl0 4 pt | Решение. Воспользуемся формулой (15.3) i(t) = = q¢(t): i(t) = (10 -6 cosl0 4 pt)¢ = 10 -6 (–sinl0 4 pt)×10 4 p = = –10 –2 psin10 4 pt. |
| i(t) = ? T = ? f = ? qm = ? im = ? |
Учитывая, что q = qmcoswt, а i = –imsinwt, легко находим значения заряда и тока:
Находим амплитуду колебаний заряда и амплитуду колебаний силы тока:
w = 10 4 p Þ 
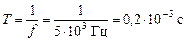
im = 10 –2 p А; w = 5×10 3 Гц; 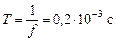
Видео:Урок 8. Перезарядка конденсатора. Плотность тока смещения. Ток смещения. Физика 11 классСкачать

Зависимость заряда на пластинах конденсатора от времени представлена уравнением вида
Идеальный колебательный контур состоит из конденсатора и катушки индуктивностью 4 мГн. Заряд на пластинах конденсатора изменяется во времени в соответствии с формулой (все величины выражены в СИ).
Установите соответствие между физическими величинами и формулами, выражающими их зависимость от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
А) сила тока i(t) в колебательном контуре
Б) энергия WL(t) магнитного поля катушки
1)
2)
3)
4)
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Сила тока в колебательном контуре равна (A — 1)
Энергия магнитного поля катушки равна (Б — 3)
📺 Видео
Урок 353. Колебательный контурСкачать

Заряд разряд конденсатораСкачать

Физика 11 класс (Урок№7 - Свободные и вынужденные электромагнитные колебания. Колебательный контур.)Скачать

Колебательный контур | ЕГЭ Физика | Николай НьютонСкачать

Свободные электромагнитные колебания. 11 класс.Скачать

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

19 Колебательный контур.Скачать

Урок 237. Электрическая емкость. КонденсаторыСкачать

11 класс урок №10 Решение задач Электромагнитные колебанияСкачать

Физика 9 класс (Урок№24 - Электромагнитные колебания. Электромагнитные волны.)Скачать

Конденсаторы в электронике. Самое понятное объяснение!Скачать

Урок 354. Математическое описание процессов в колебательном контуреСкачать

Свободные электромагнитные колебания. Практическая часть - решение задачи. 11 класс.Скачать

Физика 11 класс. Плоский конденсатор. Напряженность поля. Энергия.Скачать

Урок 226. Плоский конденсаторСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Тема 9. Решение задач по теме «Свободные электромагнитные колебания в контуре. Формула Томсона.Скачать

Свободные электромагнитные колебания. 1 часть. 9 класс.Скачать