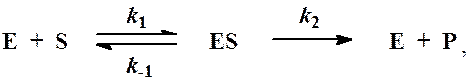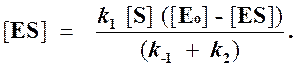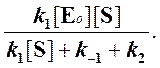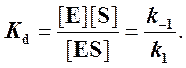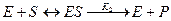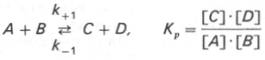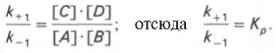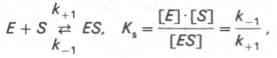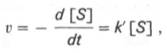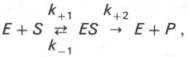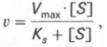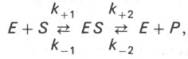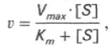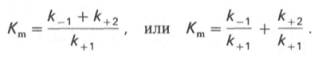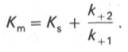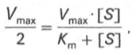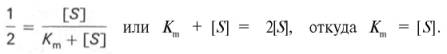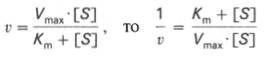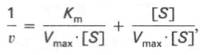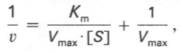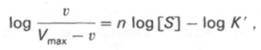Зависимость скорости ферментативной реакции от концентрации субстрата уравнение михаэлиса ментен (2 видео)

Уравнение Михаэлиса-Ментен. Ингибирование ферментов

Содержание

Страницы работы
Содержание работы
Зависимость скорости ферментативной реакции от концентрации субстрата. Уравнение Михаэлиса-Ментен.
Кинетика ферментативных реакций
💡 Видео

Страницы работы

Содержание работы

УРАВНЕНИЕ МИХАЭЛИСА —МЕНТЕН

Простейшей моделью для построения и обсуждения теорий ферментативной кинетики является кинетика односубстратных реакций. Хотя чаще всего в реакциях участвует не один, а большее число субстратов, реакцию можно рассматривать как односубстратную, если второй субстрат присутствует в очень большой концентрации. Большинство получаемых выводов можно использовать непосредственно при рассмотрении более сложных ферментативных реакций.

Как уже упоминалось, концентрация субстрата является одним из наиболее важных факторов, определяющих скорость ферментативной реакции.

В начале XX столетия Л. Михаэлисом и М. Ментен было предложено простейшее кинетическое выражение для скорости ферментативной односубстратной реакции.

Схема ферментативного процесса записывается следующим образом:

где Е — фермент; S — субстрат, подвергающийся ферментативной реакции; Р — образующийся в результате продукт;

Уравнение скорости ферментативной реакции, выведенное Михаэлисом и Ментен, предположивших, что превращение субстрата происходит только в переходном фермент-субстратном комплексе, основывается на двух предпосылках.

1. Реакция между ферментом и субстратом находится в равновесии. Это условие выполняется, если скорость распада комплекса на свободный фермент и субстрат значительно больше скорости распада его до свободного фермента и продукта (k_-1 >> k₂).

2. Концентрация свободного субстрата остается практически постоянной в течение начального периода реакции, тогда концентрация субстрата [S] может быть принята равной полной концентрации субстрата [S_o]. Это условие выполняется, если полная концентрация субстрата значительно больше полной концентрации фермента, как это обычно имеет место при кинетических исследованиях.

При высокой каталитической активности фермента реальное значение концентрации фермент-субстратного комплекса отличается от его значения в условиях равновесия. Для анализа кинетики реакции с учетом этого обстоятельства Бриггс и Холдейн предложили дополнить теорию Михаэлиса — Ментен условием стационарного состояния.

Согласно этому условию в любой момент реакции скорости образования и распада комплекса ES практически равны, так что концентрация комплекса [ES] может считаться постоянной (квазистационарной) в течение короткого периода времени, необходимого для измерения скорости. В течение более продолжительного периода времени концентрация комплекса [ES] будет изменяться по ходу реакции в связи с падением концентрации субстрата, но скорость изменения ее всегда будет существенно меньше, чем скорость ферментативной реакции.

Для стационарного состояния, при котором

k₁[E][S] – (k_-1 + k₂)·[ES] = 0

(1)

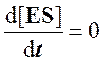
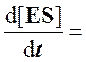
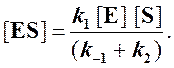
Из уравнения материального баланса для фермента

где [E_o] ─ его начальная концентрация, а [E] ─ текущая концентрация свободного, не связанного в фермент-субстратный комплекс белка, можно записать

и подставить в выражение (1):

Отсюда концентрация ES равна

[ES] =

Тогда начальная скорость ферментативной реакции, измеряемая по скорости образования продукта Р, равна

(2)

(константа Михаэлиса),

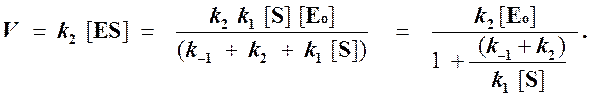
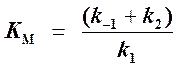
то выражение (2) можно записать в следующем виде:

(3)

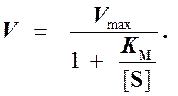
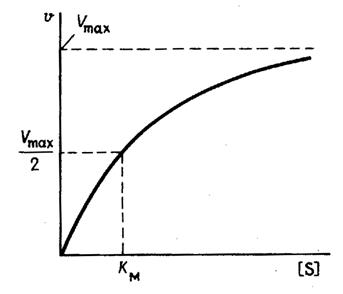
Выражение (3) называется уравнением Михаэлиса —Ментен и описывает зависимость скорости односубстратной ферментативной реакции от концентрации субстрата. Из этого уравнения видно, что при увеличении концентрации субстрата (при неизменной концентрации фермента) скорость реакции стремится к предельному значению, равному V_max.

При выводе уравнения Михаэлиса — Ментен, кроме вышеперечисленных, принимается во внимание еще несколько не совсем реальных допущений, таких как:

1) отсутствие образования значимого количества комплекса ЕР и других форм фермента;

2) необратимость второй стадии реакции, т. е. образования продукта Р. Это связано с тем, что мы рассматриваем только начальную скорость процесса, когда обратной реакцией из-за фактического отсутствия продукта еще можно пренебречь;

3) связывание с активным центром на каждой субъединице фермента только одной молекулы субстрата;

4) использование для всех реагирующих веществ вместо активностей их концентраций.

Если k₂ значительно меньше k_-1, то этим членом в выражении константы Михаэлиса можно пренебречь, и К_M становится равной отношению 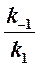, а это есть К_d (константа диссоциации фермент-субстратного комплекса):

Таким образом, являясь аналогом константы диссоциации фермент-субстратного комплекса ES, константа Михаэлиса характеризует сродство фермента к субстрату. Чем ниже К_M, тем выше сродство.

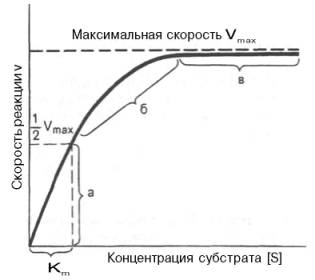
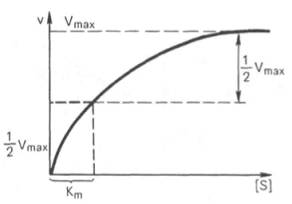
На рис. 1 приведено графическое изображение уравнения Михаэлиса — Ментен.

Рис. 1.Зависимость скорости ферментативной реакции от концентрации субстрата

Видео:Биохимия | Кинетика ферментативных реакций: константа Михаэлиса и график Лайнуивера-БеркаСкачать

Зависимость скорости ферментативной реакции от концентрации субстрата. Уравнение Михаэлиса-Ментен.

Ферменты

Ферменты — это биокатализаторы, образующиеся в клетке, и представляющие собой простые или сложные белки. Слово фермент происходит от латинского — fermentum -закваска; другое название ферментов — энзимы — происходит от греческого- enzyme — в дрожжах. В 30-х годах XX века некоторые ферменты были выделены в высокоочищенном кристаллическом состоянии. По химической природе кристаллы оказались белковыми.

История изучения ферментов тесно переплетается с историей катализа. Катализом называют ускорение химической реакции, вызванное добавлением малых нестехиометрических количеств катализатора. Катализатор ускоряет реакцию не просто своим присутствием, а взаимодействием с веществом, подвергающимся превращению, но при этом регенерируется в ходе реакции. Ферменты — биокатализаторы — не являются исключением.

Ферменты — это белки, и подобно всем белкам, они могут избирательно присоединять определенные вещества — лиганды. Лиганд, подвергающийся химическому превращению под действием фермента, называют субстратом (S), продукты (P) реакции освобождаются в раствор. Ферменты являются наиболее изученным классом белков. Это объясняется той важной ролью, которую играют ферменты: любое химическое превращение в организме происходит с их участием. К тому же, ферменты, в отличие от других белков, сравнительно легко обнаруживать и измерять их количество по катализируемой реакции.

Особенности ферментов как биокатализаторов

Ферменты как катализаторы имеют ряд особенностей:

Высокоэффективные катализаторы — ускоряют реакцию в 10 10 раз:

1 моль каталазы при 0 0 С обеспечивает разложение за 1 мин 5 млн. H₂O₂, в то время как 1 моль Pt катализирует только 250- 2000 молекул H₂O_2.

Высокоспецифичны — катализируют, как правило, реакцию одного типа или воздействуют на один субстрат. Это наиболее важное свойство ферментов.

Эффективно работают в мягких условиях.

Синтез аммиака по реакции: N₂ + 3H₂ = 2NH₃ проводят при t = 500-550 0 C, p = 10 7 -10 8 Па, ферменты, содержащиеся в бобовых культурах обеспечивают протекание подобного процесса при обычных условиях.

Ферменты — это катализаторы, работу которых можно регулировать.

Классификация ферментов по типу катализируемой реакции и номенклатура ферментов

В номенклатуре ферментов, введенной Международным биохимическим союзом (IUB) используется принцип классификации ферментов по типу катализируемой реакции и ее механизму. Основные принципы номенклатуры следующие:

Выделяют 6 классов ферментов, катализирующих 6 типов реакций:

Оксидоредуктазы.

Трансферазы.

Гидролазы.

Лиазы

Изомеразы.

Лигазы.

В каждом из 6 классов имеется несколько подклассов (от 4 до 13). Систематическое название фермента состоит из 2-х частей: названия субстрата, типа катализируемой реакции и части слова -аза.

Активный центр ферментов

Ферменты (с точки зрения строения) – это глобулярные белки, которые имеют в глобуле полость или щель определенных размеров – активный центр фермента.

Общие черты активного центра фермента:

а.ц.ф. – небольшая часть белковой молекулы;

а.ц.ф. – имеет строго определенную трехмерную структуру и размеры;

а.ц.ф. – формируется из аминокислотных остатков, удаленных в первичной структуре, но сближенных в третичной структуре;

а.ц.ф. – состоит из связывающего и каталитического участков.

Если белок сложный, то простетическая группа входит в состав а.ц. фермента.

Вся белковая молекула укладывается определенным образом в пространстве, образуя единственно возможный (термодинамически устойчивый) вариант третичной структуры данного белка, а следовательно и уникальный активный центр данного фермента.

Причины высокой каталитической активности.

Фермент поддерживает микроокружение субстрата в активном центре в состоянии отличном от его состояния в водной среде.

Располагает реагирующие атомы в правильной ориентации и на необходимом расстоянии друг от друга, чтобы обеспечить оптимальное протекание реакции.

За счет кооперативного взаимодействия субстрата и нескольких остатков аминокислот в активном центре фермент снижает энергию активации данной реакции.

Субстратная специфичность

Структура активного центра фермента комплементарна структуре субстрата, т.е. соответствует ему по 1) форме, 2) размерам и 3) способности взаимодействовать. Это является причинами высокой специфичности ферментов.

Первоначально модель активного центра, предложенная Э.Фишером, трактовала взаимодействие субстрата и фермента по аналогии с системой «ключ-замок» – модель «жесткой матрицы». Однако эта модель объясняла лишь абсолютную субстратную специфичность.

Кошланд предложил модель индуцированного соответствия. Главная черта этой модели – гибкость каталитического центра. В модели Фишера каталитический центр считается заранее подготовленным под форму молекулы-субстрата. В модели Кошланда субстрат индуцирует конформационные изменения фермента, и лишь в результате этих аминокислотные остатки и другие группы фермента принимают пространственную ориентацию, необходимую для связи с субстратом и катализа. Эта модель позволяет объяснить относительную специфичность фермента.

Каждый фермент катализирует не любые из всех возможных путей превращения субстрата, а какое-либо одно. Это свойство называется специфичностью пути превращения.

Кинетика ферментативных реакций

Зависимость скорости ферментативной реакции от концентрации субстрата. Уравнение Михаэлиса-Ментен.

Любую ферментативную реакцию схематично можно описать следующим образом:

Поведение многих ферментов при изменении концентрации субстрата описывает уравнение Михаэлиса-Ментен:

, где

— скорость ферментативной реакции,

— максимальная скорость ферментативной реакции при полном насыщении фермента субстратом,

– константа Михаэлиса,

– концентрация субстрата.

— константа образования фермент-субстратного комплекса ES,

— константа диссоциации фермент-субстратного комплекса ES.

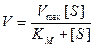
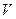
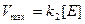
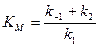
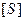
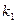
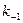
Влияние концентрации субстрата на скорость ферментативной реакции, описываемое этим уравнением, можно изобразить графически:

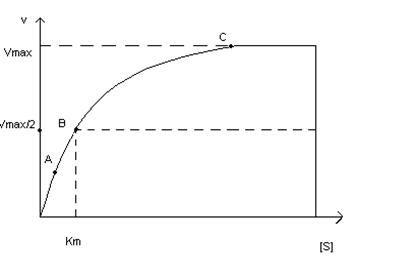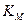
Зависимость скорости ферментативной реакции от концентрации субстрата уравнение михаэлиса ментен

равна концентрации субстрата при скорости ферментативной реакции, равной половине максимальной скорости и характеризует сродство данного фермента к тому или иному субстрату.

Некоторые ферменты требуют высокой концентрации субстрата для достижения скорости, равной максимальной, другие (например, гексокиназа) достигают 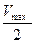при очень низкой концентрации субстрата.

Таблица.Значения констант Михаэлиса для некоторых ферментов.

Фермент	Субстрат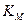
каталаза	H₂O₂
гексокиназа (мозг)	D-глюкоза	0,05
D-фруктоза	1,5
АТФ	0,4
карбоангидраза	HCO₃ —
химотрипсин	Gly-Tyr-Gly
N-бензоилтирозинамид	2,5

— скорость реакции при 25 0 С, оптимальном значении рН, полном насыщении фермента субстратом.

— число оборотов фермента, т.е. число молекул субстрата, которое превращает одна молекула фермента за 1 минуту.

Видео:Кинетика. О чем говорят графики. БиохимияСкачать

Кинетика ферментативных реакций

Одним из характерных проявлений жизни является удивительная способность живых организмов кинетически регулировать химические реакции, подавляя стремление к достижению термодинамического равновесия. Ферментативная кинетика занимается исследованием закономерностей влияния химической природы реагирующих веществ (ферментов, субстратов) и условий их взаимодействия (концентрация, рН среды, температуры, присутствие активаторов или ингибиторов) на скорость ферментативной реакции. Главной целью изучения кинетики ферментативных реакций является получение информации, которая может способствовать выяснению молекулярного механизма действия фермента.

Общие принципы кинетики химических реакций применимы и к ферментативным реакциям. Известно, что любая химическая реакция характеризуется константой термодинамического равновесия. Она выражает состояние химического равновесия, достигаемого системой, и обозначается К_р. Так, для реакции:

Рис. 4.12. Теоретический график зависимости скорости ферментативной реакции от концентрации субстрата при постоянной концентрации фермента.

а — реакция первого порядка (при [ S ]

Таким образом, константа равновесия равна отношению констант скоростей прямой и обратной реакций. Величину, обратную константе равновесия, принято называть субстратной константой, или, в случае ферментативной реакции, константой диссоциации фермент–субстратного комплекса, и обозначать символом K_S. Так, в реакции

т.е. K_Sравна отношению произведения концентрации фермента и субстрата к концентрации фермент-субстратного комплекса или отношению констант скоростей обратной и прямой реакций. Следует отметить, что константа K_Sзависит от химической природы субстрата и фермента и определяет степень их сродства. Чем ниже значение K_S, тем выше сродство фермента к субстрату.

При изучении кинетики ферментативных реакций следует учитывать одну важную особенность этих реакций (не свойственную обычным химическим реакциям), связанную с явлением насыщения фермента субстратом. При низкой концентрации субстрата зависимость скорости реакции от концентрации субстрата (рис. 4.12) является почти линейной и подчиняется кинетике первого порядка. Это означает, что скорость реакции S —> Р прямо пропорциональна концентрации субстрата S и в любой момент времени t определяется следующим кинетическим уравнением:

где [S] – молярная концентрация субстрата S; –d[S]/dt – скорость убыли субстрата; k’ – константа скорости реакции, которая в данном случае имеет размерность, обратную единице времени (мин –1 или с –1 ).

При высокой концентрации субстрата скорость реакции максимальна, становится постоянной и не зависящей от концентрации субстрата [ S ] . В этом случае реакция подчиняется кинетике нулевого порядка v = k» (при полном насыщении фермента субстратом) и целиком определяется концентрацией фермента. Различают, кроме того, реакции второго порядка, скорость которых пропорциональна произведению концентраций двух реагирующих веществ. В определенных условиях при нарушении пропорциональности говорят иногда о реакциях смешанного порядка (см. рис. 4.12).

Изучая явление насыщения, Л. Михаэлис и М. Ментен разработали общую теорию ферментативной кинетики. Они исходили из предположения, что ферментативный процесс протекает в виде следующей химической реакции:

т.е. фермент Е вступает во взаимодействие с субстратом S с образованием промежуточного комплекса ES, который далее распадается на свободный фермент и продукт реакции Р. Математическая обработка на основе закона действующих масс дала возможность вывести уравнение, названное в честь авторов уравнением Михаэлиса–Ментен, выражающее количественное соотношение между концентрацией субстрата и скоростью ферментативной реакции:

Из уравнения Михаэлиса–Ментен следует, что при высокой концентрации субстрата и низком значении K_Sскорость реакции является максимальной, т.е. v = V_max(реакция нулевого порядка, см. рис. 4.12). При низкой концентрации субстрата, напротив, скорость реакции оказывается пропорциональной концентрации субстрата в каждый данный момент (реакция первого порядка).

Следует указать, что уравнение Михаэлиса–Ментен в его классическом виде не учитывает влияние на скорость ферментативного процесса продуктов реакции, например в реакции

и носит несколько ограниченный характер. Поэтому были предприняты попытки усовершенствовать его. Так, было предложено уравнение Бриггса-Холдейна:

где К_m представляет собой константу Михаэлиса, являющуюся экспериментально определяемой величиной. Она может быть представлена следующим уравнением:

Рис. 4.13. Кривая уравнения Михаэли-са-Ментен: гиперболическая зависимость начальных скоростей катализируемой ферментом реакции от концентрации субстрата.

В числителе представлены константы скоростей распада комплекса ES в двух направлениях (в сторону исходных Е и S и в сторону конечных продуктов реакции Е и Р). Отношение k_–1/ k₊₁представляет собой константу диссоциации ферментсубстратного комплекса K_S, тогда:

Отсюда вытекает важное следствие: константа Михаэлиса всегда больше константы диссоциации фермент-субстратного комплекса K_Sна величину

Для определения численного значения К_m обычно находят ту концентрацию субстрата, при которой скорость ферментативной реакции v составляет половину от максимальной V_max, т.е. если v = 1 /₂ V_maх. Подставляя значение v в уравнение Бриггса–Холдейна, получаем:

разделив обе части уравнения на V_mах, получим

Таким образом, константа Михаэлиса численно равна концентрации субстрата (моль/л), при которой скорость данной ферментативной реакции составляет половину от максимальной.

Определение величины К_m имеет важное значение при выяснении механизма действия эффекторов на активность ферментов и т.д. Константу Михаэлиса можно вычислить по графику (рис. 4.13). Отрезок на абсциссе, соответствующий скорости, равной половине максимальной, будет представлять собой К_m.

Пользоваться графиком, построенным в прямых координатах зависимости начальной скорости реакции v₀ от начальной концентрации субстрата [S₀], неудобно, поскольку максимальная скорость V_maxявляется в данном случае асимптотической величиной и определяется недостаточно точно.

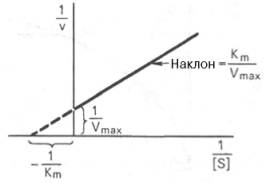
Рис. 4.14. График Лайнуивера-Бэрка.

Для более удобного графического представления экспериментальных данных Г. Лайнуивер и Д. Бэрк преобразовали уравнение Бриггса–Хол-дейна по методу двойных обратных величин исходя из того принципа, что если существует равенство между двумя какими-либо величинами, то и обратные величины также будут равны. В частности, если

то после преобразования получаем уравнение:

которое получило название уравнения Лайнуивера–Бэрка. Это уравнение прямой линии: у = ах + b. Если теперь в соответствии с этим уравнением построить график в координатах 1/v (y) от l/[S] (x), то получим прямую линию (рис. 4.14), тангенс угла наклона который будет равен величине K_m/V_max; отрезок, отсекаемый прямой от оси ординат, представляет собой l/V_max(обратная величина максимальной скорости). Если продолжить прямую линию за ось ординат, тогда на абсциссе отсекается отрезок, соответствующий обратной величине константы Михаэлиса – 1/К_m (см. рис. 4.14). Таким образом, величину К_m можно вычислить из данных наклона прямой и длины отрезка, отсекаемого от оси ординат, или из длины отрезка, отсекаемого от оси абсцисс в области отрицательных значений.

Следует подчеркнуть, что значения V_max, как и величину К_m, более точно, чем по графику, построенному в прямых координатах, можно определить по графику, построенному по методу двойных обратных величин. Поэтому данный метод нашел широкое применение в современной энзимологии. Предложены также аналогичные графические способы определения К_m и V_maxв координатах зависимости v от v/[S] и [S]/v от [S].

Следует отметить некоторые ограничения применения уравнения Ми-хаэлиса–Ментен, обусловленные множественными формами ферментов и аллостерической природой фермента. В этом случае график зависимости начальной скорости реакции от концентрации субстрата (кинетическая

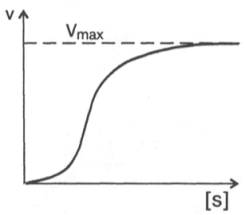
Рис. 4.15. Сигмоидная кинетическая кривая насыщения субстратом.

кривая) имеет не гиперболическую форму, а сигмоидный характер (рис. 4.15) наподобие кривой насыщения гемоглобина кислородом. Это означает, что связывание одной молекулы субстрата в одном каталитическом центре повышает связывание субстрата с другим центром, т.е. имеет место кооперативное взаимодействие, как и в случае присоединения кислорода к 4 субъединицам гемоглобина. Для оценки концентрации субстрата, при которой скорость реакции составляет половину максимальной, в условиях сигмоидного характера кинетической кривой обычно применяют преобразованное уравнение Хилла: