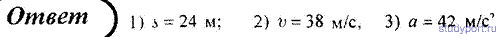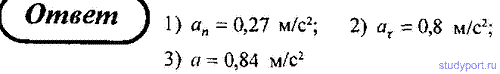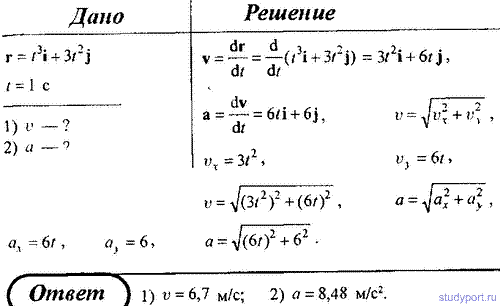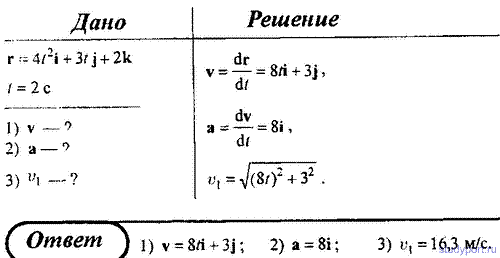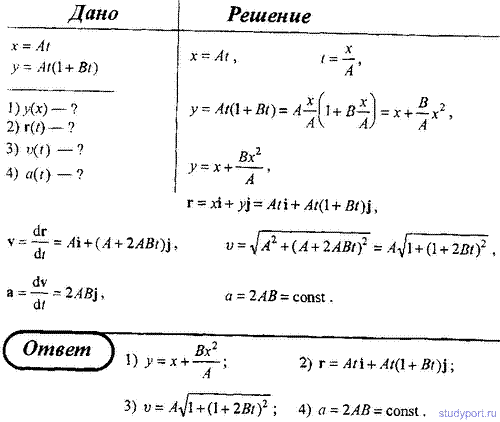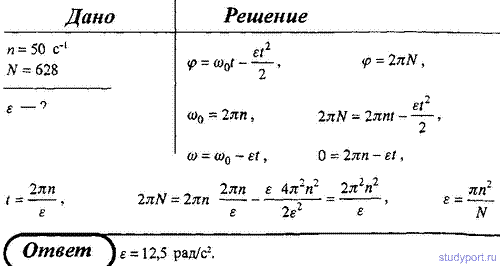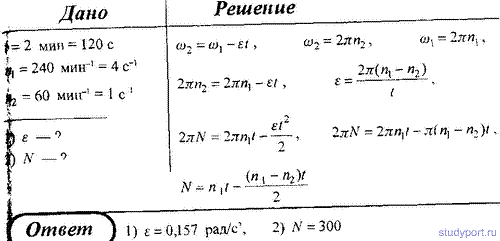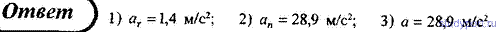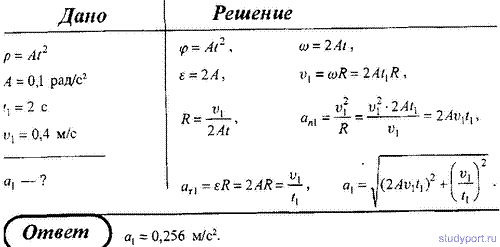Зависимость пути пройденного точкой по окружности радиусом 1 м от времени выражена уравнением (8 видео)

Кинематика

21. Тело движется равноускоренно с начальной скоростью v₀. Определить ускорение тела, если за время t оно прошло путь S и его скорость v.

22. Материальная точка движется вдоль прямой так, что её ускорение линейно растёт и за первые 10 секунд достигает значения 5 м/с 2 . Определить в конце десятой секунды: 1) скорость точки; 2) пройденный точкой путь.

23. Кинетические уравнения движения двух материальных точек имеют вид x₁ = A₁*t + B₁*t 2 + C₁*t 3 и x₂ = A₂*t + B2*t 2 + C₂*t 3 , где B₁ = 4 м/с 2 , C₁ = – 3 м/с 3 , B2 = -2 м/с 2 C2 = 1 м/c 3 . Определите момент времени, для которого ускорения этих точек будут равны.

24. Кинетические уравнения движения двух материальных точек имеют вид x₁ = A₁ + B₁*t + C₁*t 2 и x₂ = A₂ + B₂*t + C₂*t 2 , где B₁ = B₂, C₁ = – 2 м/с 2 , C₂ = 1 м/c 2 . Определить: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорение a₁ и a₂ для этого момента.

25. Нормальное ускорение точки, движущейся по окружности радиусом r = 4 м, задается уравнением a_n = A + B*t + С*t 2 (A = 1 м/c 2 , B = 6 м/с 3 , С = 9 м/с 4 ) Определите: 1) тангенсальное ускорение точки; 2) путь, пройденный точкой за время t = 5 сек. после начала движения; 3) полное ускорение для момента времени t₂ = 1 секунде.

26. Зависимость пройденного телом пути sот времени tвыражается уравнением s= At— Bt 2 + Ct 3 (A= 2 м/с, В = 3 м/с 2 , С = 4 м/с 3 ). Запишите выражения для скорости и ускорения. Определите для момента времени t— 2 с после начала движения 1) пройденный путь; 2) скорость; 3) ускорение.

27. Зависимость пройденного телом пути по окружности радиусом r= 3 м задается уравнением s= At 2 + Bt(А = 0,4 м/с : , B = 0,1 м/с) Определите для момента времени t = 1 с после начала движения ускорение: 1) нормальное, 2) тангенциальное; 3) полное.

28. Точка движется в плоскости ху из положения с координатами х₁ = v₁ = 0 со скоростью v = ai+ bxj(а, b— постоянные, i, j — орты осей x и y). Определите: 1) уравнение траектории точки y(x); 2) форму траектории.

29. Радиус-вектор материальной точки изменяется со временем по закону r = t 3 i+ 3t 2 j, где i, j — орты осей х и у. Определите для момента времени t = 1 с: 1) модуль скорости; 2) модуль ускорения.

30. Радиус-вектор материальной точки изменяется со временем по закону r = 4t 2 i+ 3tj + 2k. Определите: 1) скорость v; 2) ускорение а; 3) модуль скорости в момент времени t= 2 с.

31. Движение материальной точки в плоскости ху описывается законом х = At, у = At (1 + Bt), где A и B— положительные постоянные. Определите: 1) уравнение траектории материальной точки y(х); 2) радиус-вектор r точки в зависимости от времени; 3) скорость vточки в зависимости от времени; 4) ускорение а точки в зависимости от времени.

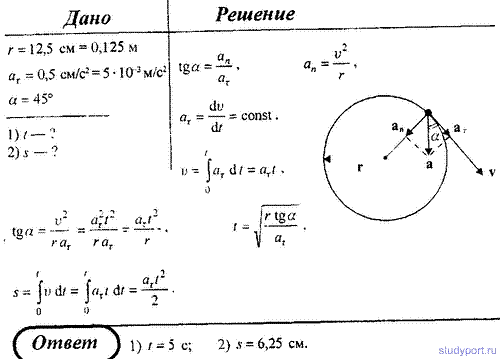
32. Материальная точка начинает двигаться по окружности радуисом r = 12,5 с постоянным тангенсальным ускорением а_τ = 0,5 см/с 2 . Определить: 1) момент времени, при котором вектор ускорения a образует с вектором скорости v угол α = 45; 2) путь, пройденный за это время движущейся точкой.

33. Линейная скорость v₁ точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость v₂точки, находящейся на 6 см ближе к его оси. Определите радиус диска.

34. Колесо вращается с постоянным угловым ускорением ε = 3рад/с. Определить радиус колеса, если через время t = 1 с после начала движения полное ускорение колеса равно а = 7,5 м/с 2 .

35. Якорь электродвигателя, имеющий частоту вращения n = 50, после выключения тока, сделав N = 628 оборотов, остановился. Определить угловое ускорение ε якоря.

36. Колесо автомобиля вращается равнозамедленно. За время t = 2 мин оно изменило частоту вращения от 240 до 60 мин -1 . Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.

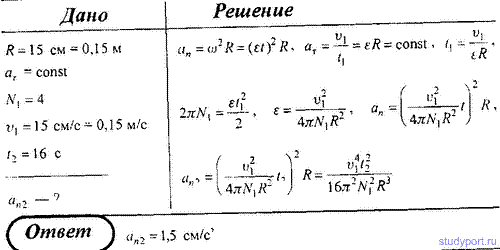
37. Точка движется по окружности радиусом R = 15 см с постоянным тангенсальным ускорением a_τ. К концу четвертого оборота после начала движения линейная скорость точки v₁ = 15 см/с. Определить нормальное ускорение a_n2 точки через t ₂ = 16 c после начала движения.

38. Диск радиусом R = 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота диска от времени задается уравнением φ = A + Bt+ Сt 2 + Dt 3 (B = 1 рад/с, C = 1 рад/с 2 , D = 1 рад/с 3 ). Определите для точек на ободе диска к концу второй секунды после начала движения: 1) тангенциальное ускорение а_τ; 2) нормальное ускорение а_n; 3) полное ускорение а.

39. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = Аt 2 (A = 0,5 рад/с 2 ). Определить к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное a_τ, нормальное a_n и полное ускорение а.

40. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = Аt 2 (A = 0,1 рад/с 2 ). Определить полное ускорение a точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки v = 0,4 м/с.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Содержание

Зависимость пути пройденного точкой по окружности радиусом 1 м от времени выражена уравнением
Материальная точка движется по окружности, радиус которой 20 м. Зависимость пути, пройденного точкой, от времени выражается уравнением S = t3 + 4t2 – t + 8.
Описание и исходные данные задания, 50% решения + фотография:
📺 Видео

Видео:Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Зависимость пути пройденного точкой по окружности радиусом 1 м от времени выражена уравнением

зависимость пройденного телом пути

Зависимость пройденного телом пути от времени задается уравнением s = A–Bt+Ct 2 +Dt 3 (A = 6 м, В = 3 м/с; С = 2 м/с 2 . D = 1 м/с 3 ). Определите для тела в интервале времени от t₁ = 1 с до t₂ = 4 с 1) среднюю скорость, 2) среднее ускорение.

Зависимость пройденного телом пути s от времени t выражается уравнением s = At–Вt 2 +Ct 3 (А = 2 м/с, В = 3 м/с 2 , С = 4 м/с 3 ). Запишите выражения для скорости и ускорения. Определите для момента времени t = 2 с после начала движения 1) пройденный путь; 2) скорость; 3) ускорение.

Зависимость пройденного телом пути по окружности радиусом r = 3 м задается уравнением s = At 2 + Bt (A = 0,4 м/с, В = 0,1 м/с). Определите для момента времени t = 1 с после начала движения ускорение: 1) нормальное, 2) тангенциальное; 3) полное.

Зависимость пройденного телом пути от времени выражается уравнением х = А – Вt 2 + Сt 3 , где А = 2 м, В = 3 м/с 2 , С = 4 м/с 3 . Определить для момента времени t = 2 с после начала движения тела: 1) пройденный путь l; 2) ускорение а; 3) среднее значение ускорения за интервал времени от t₁ = 0 с до t₂ = 2 с.

Зависимость пройденного телом пути от времени задаётся уравнением s = A + Bt + Ct 2 + Dt 3 , где B = 2 м/с 2 , C = 0,14 м/с 2 , D = 0,01 м/с 3 . В какой момент времени ускорение тела будет равно 1 м/с 2 , и чему равно среднее ускорение тела за этот промежуток времени?

Тело массой 1 кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени выражается уравнением s = t 2 + 2t + 2. Определить работу силы за 5 с после начала воздействия.

Видео:Физика - движение по окружностиСкачать

Материальная точка движется по окружности, радиус которой 20 м. Зависимость пути, пройденного точкой, от времени выражается уравнением S = t3 + 4t2 – t + 8.

Готовое решение: Заказ №8342

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 18.08.2020

Цена: 227 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

№1 1.8. Материальная точка движется по окружности, радиус которой 20 м. Зависимость пути, пройденного точкой, от времени выражается уравнением S = t3 + 4t2 – t + 8. Определить пройденный путь, угловую скорость и угловое ускорение точки через 3 с от начала её движения.

Найдём закон изменения скорости точки: . Следовательно, угловая скорость точки меняется по закону: , где – радиус окружности. Найдём закон изменения ускорения точки:

Если вам нужно решить физику, тогда нажмите ➔ заказать физику.

Похожие готовые решения:

Миномёт установлен под углом a = 60° к горизонту на крыше здания, высота которого h = 40 м. Начальная скорость мины V0 = 50 м/с. Определить время полёта мины, максимальную высоту её подъёма H, горизонтальную дальность полёта S, скорость мины в момент падения на землю.
С башни высотой 20 м брошено тело со скоростью 10 м/с под углом 60° к горизонту. Пренебрегая сопротивлением воздуха, определите время движения тела. С какой скоростью тело упадёт на землю?
Радиус-вектор материальной точки изменяется со временем по закону r = 4t i – (10t2 – 4) j. Найдите уравнение траектории движения точки. Определите перемещение и модуль перемещения материальной точки за промежуток времени от t1 = 2 c до t2 = 5 c.
Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса. Условие 2 1.22. Колесо, вращаясь равноускоренно, достигло угловой скорости w = 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.