Зависимость давления насыщенных паров толуола от температуры выражается уравнением (3 видео)

Определение давления насыщенных паров углеводородов при различных температурах по графику Кокса

График Кокса, представленный на рис. 7.1, построен для индивидуальных парафиновых углеводородов нормального строения. Для соединений одного гомологического ряда или одной химической природы получается ряд прямых, сходящихся в одной точке, — полюсе. Однако этим графиком широко пользуются в технологических расчетах применительно к узким нефтяным фракциям.

По данному графику можно находить давление насыщенных паров фракции при заданной температуре, если известно давление насыщенных паров при какой-либо другой температуре. Можно также найти температуру кипения нефтяной фракции при заданном давлении, если известна температура кипения при каком-либо другом давлении.

Например [5, с. 43], требуется определить температуру кипения нефтяной фракции при атмосферном давлении, если известно, что при остаточном давлении 75 мм рт. ст. фракция кипит при температуре 260 °C. Для этого по графику на рис. 7.1 из точки, соответствующей 75 мм рт. ст. на оси абсцисс, восстанавливаем перпендикуляр до пересечения с горизонталью, исходящей из точки с температурой 260 °C на оси ординат. Из точки пересечения проводим

Давление насыщенных паров, мм рт. ст.

Рис. 7.1. График Кокса для пересчета давления насыщенных паров с одной температуры на другую [5, рис. 4]

юоооот линию вдоль лучей C_|8H_3S и С₂₀Н₄₂ до пересечения с перпендикуляром, восстановленным из точки 760 мм рт. ст. Через полученную точку пересечения А проводим горизонталь и на оси ординат находим температуру кипения данной фракции при атмосферном давлении, составившую 357 °C.

Содержание

Определение давления насыщенных паров некоторых алканов, алкенов, ароматических углеводородов
Бинарные жидкие системы
Зависимость давления насыщенных паров толуола от температуры выражается уравнением
💥 Видео

Видео:Урок 188. Температурная зависимость давления пара. Точка росыСкачать

Определение давления насыщенных паров некоторых алканов, алкенов, ароматических углеводородов

некоторых алканов, алкенов, ароматических углеводородов

Давление насыщенных паров некоторых алканов и алкенов можно определить по графическим зависимостям, представленным на рис. 7.2, а ряда ароматических углеводородов — по графикам на рис. 7.3.

Рис. 7.2. Определение давления насыщенных паров некоторых алканов, алкенов и нефтепродуктов [2, рис. 2.17]:

I — этилен; 2 — этан; 3 — пропен; 4 — пропан; 5 — 1-бутен; 6 — бутан; 7 — пентан; 8 — гексан; 9 — гептан; 10 — октан;

II — нонан; 12 — декан; 13 — ундекан; 14 — додекан; 15 — тетрадекан; 16 — гексадекан; 17 — октадекан; 18 — эйкозан;

19 — тетракозан; 20 — триаконтан

Рис. 7.3. Определение давления насыщенных паров ароматических углеводородов [2, рис. 2.18]:

1 — бензол; 2 — толуол; 3 — этилбензол; 4 — о-ксилол; 5 — пронилбензол; 6 — изопропилбензол; 7 — фенол; 8 — нафталин; 9 — дифенил; 10 — флуорен; 11 — антрацен

Видео:Насыщенный пар. Зависимость давления пара от температуры | Физика 10 класс #35 | ИнфоурокСкачать

Бинарные жидкие системы

Жидкое состояние является промежуточным между газообразным и твердым. С газами жидкости сближает прежде всего их изотропность (одинаковость физических свойств по всем направлениям) и текучесть (способность легко изменять внешнюю форму под воздействием малых нагрузок). Однако высокая плотность и малая сжимаемость жидкостей приближает их к твердым телам. Способность жидкостей легко изменять свою форму говорит об отсутствии в них жестких сил межмолекулярного взаимодействия. В то же время низкая сжимаемость жидкостей, обусловливающая способность сохранять постоянный при данной температуре объем, указывает на присутствие хотя и не жестких, но все же значительных сил взаимодействия между частицами.

Для каждого агрегатного состояния характерно свое соотношение между потенциальной и кинетической энергиями частиц вещества. У твердых тел средняя потенциальная энергия частиц больше их средней кинетической энергии. Поэтому в твердых телах частицы занимают определенные положения друг относительно друга и лишь колеблются около этих положений. Для газов соотношение энергий обратное, вследствие чего молекулы газа всегда находятся в состоянии хаотического движения, и силы сцепления между молекулами практически отсутствуют, так что газ всегда занимает весь предоставленный ему объем. В случае жидкостей кинетическая и потенциальная энергия частиц приблизительно одинаковые, т.е. частицы связаны друг с другом, но не жестко. Поэтому жидкости текучи, но имеют постоянный при данной температуре объем.

В большинстве жидкостей наблюдается ближний порядок – число ближайших соседей у каждой молекулы и их взаимное расположение приблизительно одинаковы во всем объеме данной жидкости. У жидкостей сильно выражена самодиффузия, т.е. непрерывные переходы молекул с места на место. Физико-химические свойства жидкости зависят от природы образующих ее частиц и от интенсивности их взаимодействия между собой.

Внутренне строение жидкостей выяснено только в самых общих чертах, и до настоящего времени не создано общей теории жидкого состояния. Объясняется это тем, что внутреннее строение жидкостей значительно сложнее внутреннего строения газов и кристаллов. По сравнению с газами жидкости обладают прежде всего во много раз большей плотностью. Расстояния между молекулами в жидкости настолько малы, что свойства жидкости в значительной степени определяются собственным объемом молекул и взаимным притяжением между ними, в то время как в газах в обычных условиях влияние этих факторов незначительно. При малых расстояниях между молекулами имеют значение также их геометрическая форма и полярные свойства. Свойства полярных жидкостей зависят не только от взаимодействия молекулы с молекулой, но и от взаимодействия между отдельными частями разных молекул.

Когда молекулы жидкости обладают полярностью, то, кроме взаимного притяжения между ними, свойственного и неполярным молекулам, проявляется и взаимодействие между разными частями молекул, несущими электрический заряд. Это делает неравноценным различные положения молекул. Так, положение, отвечающее взаимному отталкиванию обоих концов молекул (рис. 8.1. а), будет неустойчивым. Точнее, при сколько-нибудь значительной полярности молекул это положение не сможет возникнуть вследствие взаимного отталкивания молекул уже при сближении их в таком положении. Наоборот, положение, которое отвечает усилению взаимного притяжения между молекулами (рис. 8.1. б), является преимущественным и будет сохраняться более продолжительное время.

Оно соответствует большей взаимной связанности

<img src="http://ic3.static.km.ru/img/65151

002.jpg» /> <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

002.jpg» /> молекул, и образование его

<img src="http://ic3.static.km.ru/img/65151

002.jpg» /> <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

004.jpg» /> сопровождается выделением

а б Подобный комплекс из

полярных молекул может

содержать не только две

Рис. 8.1 Взаимное положение молекулы, но и большее чис-

полярных молекул в жидкости: ло их. Явление образования

а) – неустойчивое (отталкивание); таких комплексов получило

б) – устойчивое (притяжение). название ассоциации (объеди-

нение). К ассоциированным жидкостям относятся вода, спирты, ацетон, сжиженный аммиак и др. Степень ассоциации бывает различной. Сильно ассоциированные жидкости заметно отличаются от нормальных по многим свойствам. Ассоциация вызывает увеличение теплоты испарения, уменьшает летучесть жидкости и соответственно изменяет другие свойства.

Впрочем, при обычных температурах одного дипольного взаимодействия недостаточно, чтобы вызвать такую высокую степень ассоциации, которая наблюдается, например, между молекулами воды, аммиака и других сильно полярных жидкостей. Основной причиной ассоциации в этих условиях служит образование между молекулами водородной связи.

Испарение – это процесс перехода молекул вещества со свободной поверхности жидкости в газовую фазу при температуре ниже точки кипения.

По мере нагревания жидкости достигается такая температура, при которой во всем объеме жидкости возникают пузырьки пара. Процесс парообразования при этом резко ускоряется. Его интенсивность определяется количеством тепла, подводимого к жидкости. Этот процесс называется кипением, а температура – соответственно, температурой кипения.

Чем выше температура кипения жидкости, тем при нормальных условиях меньше пара над ней образуется в единицу времени.

При испарении жидкости со свободной поверхности затраты энергии восполняются подводом тепла из окружающей среды, если ее температура выше, чем у жидкости. Если же исходные температуры жидкости и окружающего воздуха одинаковы, то испарение будет сопровождаться понижением внутренней энергии жидкости, что приводит к постепенному понижению ее температуры. Данное понижение тем больше, чем выше удельная теплота ее испарения и чем интенсивнее процесс парообразования. Так например, в комнатных условиях при испарении горючих жидкостей таких как СН3ОН (метанол), СН3СОСН3 (ацетон) и С2Н5ОС2Н5 (диэтиловый эфир) их температура понижается на 7-10 оС относительно окружающего воздуха. Эта закономерность сохраняется и при горении перечисленных выше веществ, поскольку затраты тепла на испарение не компенсируются тепловым потоком от факела пламени.

Если испарение протекает в закрытом сосуде, то через некоторое время наступает равновесие между числом молекул, покинувших и вернувшихся обратно в жидкость. Наступает динамическое равновесие. Пар, находящийся в динамическом равновесии с жидкостью, называется насыщенным паром.

Давление насыщенного пара жидкостей и его зависимость от температуры

Жидкости испаряются при любой температуре при наличии свободного объема. Испарение происходит с поверхности, причем тех молекул, которые имеют повышенную в 5-10 раз энергию по сравнению со средней.

Если испарение протекает в закрытом сосуде, то образующийся пар производит давление на стенки сосуда и жидкость, т.е. пар обладает давлением <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

006.gif» />. Давление насыщенного пара является характерной величиной для жидкости при данной температуре и приводится в справочной литературе.

Давление насыщенного пара жидкости с повышением температуры увеличивается (рис. 8.2), и как только оно станет равным атмосферному, жидкость закипает. Из рис. 8.2 видно, что давление насыщенного пара закономерно повышается с увеличением температуры. При одинаковом внешнем давлении жидкости закипают при различной температуре, так как имеют неодинаковое давление насыщенного пара.

<img src="http://ic3.static.km.ru/img/65151

007.gif» /><img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

008.gif» /><img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

007.gif» /> ацетон этанол вода

Температура, оС

<img src="http://ic3.static.km.ru/img/65151

010.gif» />

Рис. 8.2 Зависимость давления насыщенного пара (Р×10-5 Па.) жидкости от температуры (ацетон, этиловый спирт, вода – соответственно).

Если изменить внешнее давление, то температура кипения жидкости будет изменяться. С повышением внешнего давления температура кипения увеличивается, а с понижением (вакуум) – уменьшается. При определенной величине внешнего давления жидкость может кипеть при комнатной температуре.

Зависимость давления насыщенного пара от температуры выражается уравнением Клаузиуса – Клапейрона

<img src="http://ic3.static.km.ru/img/65151

где <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

014.gif» /> — мольная энтальпия испарения, <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

016.gif» />; <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

018.gif» /> — мольное изменение объема в процессе испарения, равное <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

При испарении жидкости резко изменяется объем паровой фазы по сравнению с жидкой. Так, при испарении 1<img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

022.gif» /> воды при 25 оС и давлении 760 мм рт. ст. образуется 1244 <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

022.gif» />пара, т.е. объем увеличился в 1244 раза. Поэтому в уравнении объемом жидкости можно пренебречь: <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

024.gif» />, <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

<img src="http://ic3.static.km.ru/img/65151

С учетом уравнения Менделеева–Клапейрона <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

030.gif» /> и тогда

<img src="http://ic3.static.km.ru/img/65151

032.gif» /><img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

Интегрирование уравнения (8.3) приводит к формуле

<img src="http://ic3.static.km.ru/img/65151

Эта формула носит имя двух ученых – Клаузиуса и Клапейрона, которые вывели ее из различных исходных положений.

Формула Клаузиуса–Клапейрона применима ко всем фазовым переходам, включая плавление, испарение и растворение вещества.

Теплота испарения жидкости <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

037.gif» /><img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

039.gif» /> — это количество теплоты, поглощаемое жидкостью при изотермическом испарении. Различают мольную теплоту испарения и удельную теплоту испарения (относящуюся к 1 г жидкости). Чем выше теплота испарения, тем жидкость при прочих равных условиях испаряется медленнее, так как молекулам приходится преодолевать большие силы межмолекулярного взаимодействия.

Сопоставление теплот испарения может быть более простым, если их рассматривать при постоянной температуре.

Для определения <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

039.gif» /> широко используется правило Трутона: мольная теплота испарения при атмосферном давлении (Р = const) различных жидкостей прямо пропорциональна их температуре кипения Ткип

<img src="http://ic3.static.km.ru/img/65151

042.gif» /> или <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

Коэффициент пропорциональности называется коэффициентом Трутона и для большинства нормальных (неассоциированных) жидкостей равен 88,2 — 92,4 <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

Теплота испарения данной жидкости зависит от температуры. С повышением температуры она понижается и при критической температуре становится равной нулю.

В инженерных расчетах используется эмпирическое уравнение Антуана

<img src="http://ic3.static.km.ru/img/65151

где А, В, <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

050.gif» /> — константы, характеризующие вещество.

Найденные зависимости давления насыщенного пара от температуры используются в пожарно–технических расчетах для вычисления концентра- ции пара (<img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

052.gif» />; %), температурных пределов распространения пламени

<img src="http://ic3.static.km.ru/img/65151

В условиях пожара жидкости испаряются в окружающее пространство. Скорость испарения жидкости при этом определяет скорость ее выгорания. В этом случае на скорость испарения решающее влияние оказывает количество тепла, поступающее из зоны горения.

Скорость выгорания жидкостей непостоянна. Она зависит от начальной температуры жидкости, диаметра резервуара, уровня жидкости в нем, скорости ветра и т.д.

Давление насыщенного пара над растворами неограниченно смешивающихся жидкостей

В практике широко используются многочисленные растворы, состоящие из двух и более хорошо растворимых друг в друге жидкостей. Наиболее простыми являются смеси (растворы), состоящие из двух жидкостей – бинарные смеси. Закономерности, найденные для таких смесей, можно использовать и для более сложных. К таким бинарным смесям можно отнести: бензол-толуол, спирт-эфир, ацетон-вода, спирт-вода и т.д. В этом случае в паровой фазе содержатся оба компонента. Давление насыщенного пара смеси будет слагаться из парциальных давлений компонентов. Так как переход растворителя из смеси в парообразное состояние, выражаемое его парциальным давлением, тем значительнее, чем больше содержание его молекул в растворе, Рауль нашел, что «парциальное давление насыщенного пара растворителя над раствором равно произведению давления насыщенного пара над чистым растворителем при той же температуре на его мольную долю в растворе»:

<img src="http://ic3.static.km.ru/img/65151

где <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

058.gif» /> — давление насыщенного пара растворителя над смесью; <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

060.gif» />- давление насыщенного пара над чистым растворителем; N – мольная доля растворителя в смеси.

Уравнение (8.6) является математическим выражением закона Рауля. Для описания поведения летучего растворенного вещества (второго компонента бинарной системы) применяется это же выражение:

<img src="http://ic3.static.km.ru/img/65151

Общее давление насыщенного пара над раствором будет равно (закон Дальтона):

<img src="http://ic3.static.km.ru/img/65151

Зависимость парциального и общего давления паров смеси от ее состава показана на рис. 8.3, где на оси ординат отложено давление насыщенных паров, а на оси абсцисс – состав раствора в мольных долях. При этом по оси абсцисс содержание одного вещества (А) убывает слева направо от 1,0 до 0 мольных долей, а содержание второго компонента (В) одновременно в том же направлении увеличивается от 0 до 1,0. При каждом определенном составе общее давление насыщенного пара равняется сумме парциальных давлений. Общее давление смеси изменяется от давления насыщенного пара одной индивидуальной жидкости <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

066.gif» /> до давления насыщенного пара второй чистой жидкости<img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

Законы Рауля и Дальтона часто используются для оценки пожарной опасности смесей жидкостей.

<img src="http://ic3.static.km.ru/img/65151

Состав смеси, мольные доли

Рис. 8.3 Диаграмма состав раствора – давление насыщенного пара

Обычно состав паровой фазы не совпадает с составом жидкой фазы и паровая фаза обогащена более летучим компонентом. Это различие можно изобразить и графически (график имеет вид аналогичный графику на рис. 8.4, только на оси ординат взята не температура а давление).

В диаграммах, представляющих зависимость температур кипения от состава (диаграмма состав-температура кипения рис. 8.4), обычно принято строить две кривые, одна из которых связывает эти температуры с составом жидкой фазы, а другая с составом пара. Нижняя кривая относится к составам жидкости (кривая жидкости), а верхняя – к составам пара (кривая пара).

Поле, заключенное между двумя кривыми, соответствует двухфазной системе. Любая точка, находящаяся в этом поле, отвечает равновесию двух фаз – раствора и насыщенного пара. Состав равновесных фаз определяется координатами точек, лежащих на пересечении изотермы, проходящей через кривые, и данную точку.

При температуре t1 (при данном давлении) будет кипеть жидкий раствор состава х1 (точка а1 на кривой жидкости), пар, равновесный с этим раствором, обладает составом х2 (точка b1 на кривой пара).

Т.е. жидкости состава x1 будет соответствовать пар состава х2.

Исходя из выражений: <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

072.gif» />, <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

074.gif» />, <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

076.gif» />, <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

взаимосвязь между составом жидкой и паровой фаз может быть выражена соотношением:

<img src="http://ic3.static.km.ru/img/65151

Рис. 8.4. Диаграмма состав-температура кипения двойных смесей.

Реальное давление насыщенного пара индивидуальной жидкости при данной температуре есть характерная величина. Практически нет жидкостей, которые бы обладали одинаковыми значениями давления насыщенного пара при одной и той же температуре. Поэтому <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

084.gif» /> всегда больше или меньше <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

086.gif» />. Если <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

084.gif» />><img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

086.gif» />, то <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

090.gif» />><img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/65151

092.gif» />, т.е. состав паровой фазы обогащен компонентом А. Изучая растворы, Д.П. Коновалов (1881г.) сделал обобщение, получившее название первого закона Коновалова.

В двойной системе пар, по сравнению с находящейся с ним в равновесии жидкостью, относительно богаче тем из компонентов, прибавление которого к системе повышает общее давление пара, т.е. понижает температуру кипения смеси при данном давлении.

Первый закон Коновалова является теоретической основой для разделения жидких растворов на исходные компоненты путем фракционной перегонки. Например, система, характеризуемая точкой К, состоит из двух равновесных фаз, состав которых определяется точками a и b: точка а характеризует состав насыщенного пара, точка b — состав раствора.

По графику можно провести сопоставления составов паровых и жидких фаз для любой точки, заключенной в плоскости между кривыми.

Реальные растворы. Закон Рауля не выполняется для реальных растворов. Отклонение от закона Рауля существует двух типов:

парциальное давление растворов больше давлений или летучести паров идеальных растворов. Общее давление пара больше аддитивной величины. Такие отклонения называются положительными, например, для смесей (рис. 8.5 а, б) CH3COCH3-C2H5OH, CH3COCH3-CS2, C6H6- CH3COCH3, H2O-CH3OH, C2H5OH-CH3OCH3, CCl4-C6H6 и др.;

<img src="http://ic3.static.km.ru/img/65151

Рис. 8.5. Зависимость общего и парциальных давлений пара от состава:

а – для смесей с положительным отклонением от закона Рауля;

б – для смесей с отрицательным отклонением от закона Рауля.

парциальное давление растворов меньше давлений паров идеальных растворов. Общее давление пара меньше аддитивной величины. Такие отклонения называются отрицательными. Например, для смеси: H2O-HNO3; H2O-HCl; CHCl3-(CH3)2CO; CHCl3-C6H6 и т.д.

Положительные отклонения наблюдаются в растворах, у которых разнородные молекулы взаимодействуют с меньшей силой, чем однородные.

Это облегчает переход молекул из раствора в паровую фазу. Растворы с положительным отклонением образуются с поглощением теплоты, т.е. теплота смешения чистых компонентов будет положительной, происходит увеличение объема, уменьшение ассоциации.

Отрицательные отклонения от закона Рауля возникают в растворах, у которых происходит усиление взаимодействия разнородных молекул, сольватация, образование водородных связей, образование химических соединений. Это затрудняет переход молекул из раствора в газовую фазу.

Сущность разделения (разгонки) бинарных жидких растворов

Как можно разделить бинарную смесь на составляющие компоненты? Предложим, что смесь состоит из воды и ацетона в соотношении 1:1.

Для разделения смеси необходимо (рис. 8.6):

1. нагреть смесь до кипения с целью увеличения скорости испарения жидкости.

2. образовавшуюся паровую фазу сконденсировать.

Как меняется состав разделяющейся смеси и как изменяется состав конденсата в ходе кипячения?

<img src="http://ic3.static.km.ru/img/65151

099.gif» />

Рис. 8.6 Перегонный аппарат: 1 – термометр; 2 – колба для перегонки;

3 – холодильник; 4 – приемник; 5 – дистиллят.

По мере кипения состав бинарной смеси во времени изменяется. Это связано с тем, что летучий компонент (ацетон), имея большее парциальное давление, в большей мере поступает в паровую фазу, а поэтому его содержание в жидкой фазе уменьшается.

Состав конденсата во времени также изменяется (рис. 8.7). В начальный период конденсат в своем составе содержит главным образом летучий компонент, затем его концентрация во времени постепенно понижается, одновременно растет концентрация высококипящего компонента.

Если всю смесь превратить в пар и собрать в виде конденсата, то состав ее не изменится.

Чтобы разделить смесь, необходимо произвести отбор конденсата в определенный период, разделяя его по времени на несколько частей. Первая часть будет состоять, в основном, из летучего компонента, вторая – обогащенная летучим компонентом, последующие части будут содержать высококипящий компонент в большем количестве. Каждую часть вновь нагреть до кипения и конденсат собрать в различные отрезки времени. Проделав так несколько раз, можно получить отдельные компоненты исходной смеси.

Изменение состава жидкой и паровой фаз при различных температурах кипения можно показать на диаграмме температура кипения – состав жидкой и паровой фаз.

Рассмотрим диаграмму состояния для жидкого раствора в координатах температура кипения – состав (C6H6+C6H5CH3). Проследим за фракционной перегонкой раствора бензол – толуол (рис. 8.9).

<img src="http://ic3.static.km.ru/img/65151

Рис. 8.7 Изменение состава жидкой фазы в перегонной колбе во времени.

Кривая в координатах температура кипения – состав дает возможность найти температуру кипения раствора при любой концентрации жидкой фазы. Например, температура кипения раствора, содержащего 32% (мольных) бензола, будет соответствовать 98 °С. Получившийся при этом пар будет состоять также из бензола и толуола, но их концентрации будут иными, чем в жидкой фазе.

<img src="http://ic3.static.km.ru/img/65151

Рис. 8.8 Изменение состава дистиллята во времени.

Для определения состава паровой фазы по графику при любой температуре кипения смеси проводят изотерму. В точках пересечения кривых жидкости и пара опускают перпендикуляры и определяют состав паровой и жидкой фаз.

<img src="http://ic3.static.km.ru/img/65151

Рис. 8.9 Фракционная перегонка раствора бензол – толуол.

При температуре 98 °С концентрация бензола в парах будет равна 53%. Таким образом видно, что при кипении паровая фаза обогащается легкой фракцией (с 32% в жидкости до 53% в паре).

Если получившийся пар сконденсировать и снова нагреть до температуры кипения, то в паровой фазе бензола станет уже 80%. Таким образом, чередуя процессы испарения с конденсацией, можно разделить компоненты раствора. Этот принцип лежит в основе ректификации.

Ректификация – процесс одновременного испарения раствора и частичной конденсации паров, осуществляемый в одном аппарате – ректификационной колонне.

Разгонка жидкостей происходит самопроизвольно в процессе горения бензинов, нефти, представляющих собой сложные смеси углеводородов. Причем процесс разгонки идет только в верхнем слое горящей жидкости. При этом в большей степени выделяются в зону горения летучие фракции, состав жидкой фазы обогащается высококипящими компонентами. Процесс разделения может идти до образования коксовых остатков.

Азеотропные смеси. Второй закон Коновалова

Однако не все смеси можно разделить обычной ректификацией. Есть смеси, которые не разделяются при разгонке, например, не разделяются смеси состава: бензол (60%) – метанол (40%); спирт этиловый (96%) – вода (4%) и т.д.

Температуры кипения некоторых азеотропных смесей приведены в табл. 8.1. Эти смеси имеют постоянную точку кипения, которая может быть выше или ниже температуры кипения высококипящего и низкокипящего компонентов раствора.

Коновалов Д.П. установил, что причиной невозможности разделения азеотропных смесей является совпадение состава жидкой и паровой фаз.

Если взять смесь состава «С», имеющего азеотроп с минимумом температуры кипения (рис. 8.10), и начать нагревать, то в паровую фазу будет в основном переходить азеотроп, а жидкая фаза будет обогащаться компонентом А.

Если взять эту же смесь состава «К», то при нагревании вновь в паровую фазу будет в основном переходить азеотроп, жидкая фаза будет обогащаться компонентом В.

Видео:ЕГЭ по физике. Теория #28. Влажность воздуха. Насыщенный парСкачать

Зависимость давления насыщенных паров толуола от температуры выражается уравнением

6. Фазовое равновесие в однокомпонентных системах

Условием равновесия между двумя фазами является равенство давления, температуры и химических потенциалов (мольных энергий Гиббса) в обеих фазах. Если температура изменяется при постоянном давлении или давление изменяется при постоянной температуре, то равновесие нарушается и одна из фаз исчезает. Изменение химических потенциалов фаз при этом можно рассчитать по уравнениям:

, (6.1)

, (6.2)

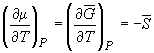
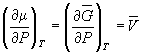
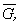
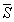
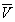
где и – мольные энергия Гиббса, энтропия и объем.

Условие сосуществования двух фаз при одновременном изменении давления P и температуры T описывается уравнением Клапейрона:

, (6.3)

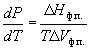
где H_ф.п. – мольная энтальпия равновесного фазового перехода (плавление, испарение, возгонка, переход между модификациями), V_ф.п. – разность мольных объемов фаз, находящихся в равновесии.

В случаях испарения и возгонки уравнение (6.3) можно упростить, считая, что мольным объемом конденсированной фазы (жидкости или твердого тела) V_к.ф. по сравнению с мольным объемом пара V_пар можно пренебречь и что пар подчиняется уравнению состояния идеального газа. Подставляя (V_пар – V_к.ф.) V_пар и V_пар = RT/P, получаем уравнение Клаузиуса-Клапейрона:

(6.4)

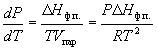
или после преобразования

. (6.5)

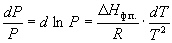
Интегрирование в предположении, что H_ф.п. не зависит от температуры (что справедливо в узких интервалах температур), дает

(6.6)

(6.7)

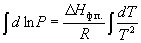
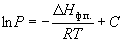
где C – константа интегрирования. Следовательно, зависимость lnP от 1/Т должна быть линейной, а наклон прямой равен – H_ф.п./R.

(6.8)

(6.9)

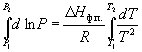
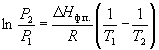
По этому уравнению можно рассчитать энтальпию испарения или возгонки, исходя из значений давления пара при двух разных температурах.

Мольные энтальпии возгонки, плавления и испарения при данной температуре связаны соотношением

_возгH = _плH + _испH (6.10)

Энтальпию испарения жидкости можно приближенно оценить по правилу Трутона, согласно которому мольная энтропия испарения в нормальной точке кипения (при 1 атм) приблизительно постоянна:

_испS = 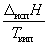88 Дж . моль –1 . К –1 (6.11)

Правило хорошо выполняется для неполярных жидкостей.

Зависимость энтальпии фазового перехода от температуры можно рассчитать по закону Кирхгофа:

(6.12)

(6.13)

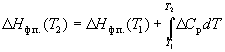
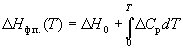
где C_p – разность теплоемкостей фаз, находящихся в равновесии, H₀ – константа интегрирования, определяемая из известных значений H_ф.п. и C_p. Для небольших интервалов температуры можно считать, что C_p = const. В этом случае из уравнения (6.13) получаем:

H_ф.п. (T) = H₀ + T C_p. (6.14)

Подставляя уравнение (6.14) в уравнение (6.7), получаем:

, (6.15)

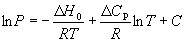
в котором С определяют из известных значений P, H₀ и C_p.

Пример 6-1. Рассчитать изменение давления, необходимое для изменения температуры плавления льда на 1 o C. При 0 o C энтальпия плавления льда равна 333.5 Дж . г –1 , удельные объемы жидкой воды и льда равны V_ж. = 1.0002 см 3 . г –1 и V_тв. = 1.0908 см 3 . г –1 .

Решение. Изменение объема при плавлении льда равно

V_ж. – V_тв. = 1.0002 – 1.0908 = –0.0906 см 3 . г –1 = –9.06 10 –8 м 3 . г –1 .

= –1.348 10 7 (Па . К –1 ) = –133 атм . К –1 .

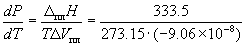
Таким образом, при повышении давления на 133 атм температура плавления льда понижается на 1 градус. Знак «минус» показывает, что при повышении давления температура плавления понижается.

Ответ. P = 133 атм.

Пример 6-2. Рассчитать давление пара жидкого брома при 25 o C. _fG o газообразного брома равна 3.110 кДж . моль –1 .

Решение. _испG o брома равно _fG o [Br₂ (г)] = 3110 Дж . моль –1 .

_испG o = 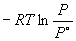, откуда P = 0.2852 атм.

Ответ. P = 0.2852 атм.

Пример 6-3. Рассчитать давление, при котором графит и алмаз находятся в равновесии при 25 o C. _fG o алмаза равна 2.900 кДж . моль –1 . Считать плотности графита и алмаза равными 2.25 и 3.51 г . см –3 соответственно и не зависящими от давления.

Решение. Изменение объема при переходе от графита к алмазу равно

V = 12 . 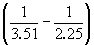10 –6 = –1.91 10 –6 м 3 . моль –1

При начальном давлении P₁ разность мольных энергий Гиббса G₁ = 2900 Дж . моль –1 , а при конечном давлении P₂ разность G₂ =0.

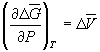
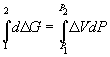
Поскольку , то = G₂ – G₁ = V(P₂ – P₁).

Отсюда P₂ = 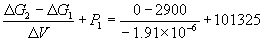= 1.52 10 9 Па = 1.5 10 4 атм.

Ответ. P = 1.5 10 4 атм.

Пример 6-4. Температура кипения бензола при давлении 1 атм равна 80.1 o C. Оценить давление пара бензола при 25 o C.

Решение. Давление пара бензола при T₁ = 353.3 K равно P₁ = 1 атм. По правилу Трутона _испH = 88 . 353.3 = 31.1 кДж . моль –1 . Подставим эти данные в уравнение (6.9). Получим:

, откуда P₂ = 0.141 атм.

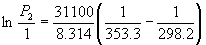
ЗАДАЧИ

Рассчитать давление, при котором две формы CaCO₃ – кальцит и арагонит – находятся в равновесии при 25 o C. _fG o кальцита и арагонита при 25 o C равны –1128.79 и –1127.75 кДж . моль –1 соответственно. Считать, что плотности кальцита и арагонита равны 2.71 и 2.93 г . см –3 соответственно и не зависят от давления.
Рассчитать температуру, при которой две формы CaCO₃ – кальцит и арагонит – находятся в равновесии при давлении 1 атм. При 25 o C _fG o кальцита и арагонита равны –1128.79 и –1127.75 кДж . моль –1 соответственно, _fH o равны–1206.92 и –1207.13 кДж . моль –1 соответственно. Считать, что C_P = 0.
_fG o жидкой и газообразной воды при 25 o C равны –237.129 и –228.572 кДж . моль –1 соответственно. Рассчитать давление пара воды при 25 o C.
Плотности жидкого и твердого олова при температуре плавления (231.9 o C) равны 6.980 г . см –3 и 7.184 г . см –3 соответственно. Энтальпия плавления олова равна 1.690 ккал . моль –1 . Определить температуру плавления олова под давлением 500 атм. Молярная масса олова равна 118.7 г . моль –1 .
При замерзании бензола (5.5 o C) его плотность изменяется от 0.879 г . см –3 до 0.891 г . см –3 . Энтальпия плавления равна 10.59 кДж . моль –1 . Определить температуру плавления бензола при давлении 1000 атм.
Плотности жидкой и твердой ртути при температуре плавления
(–38.87 o C) равны 13.690 и 14.193 г . см –3 соответственно. Энтальпия плавления ртути равна 2.33 кал . г –1 . Определить температуру плавления ртути при давлении 3000 атм.
Температура кипения жидкого метанола равна 34.7 o C при давлении 200 мм рт. ст. и 49.9 o C при давлении 400 мм рт. ст. Найти температуру кипения метанола при нормальном давлении.
Давление пара диэтилового эфира при 10 o C равно 286.8 мм рт. ст., а при 20 o C – 432.8 мм рт. ст. Определить мольную энтальпию испарения и нормальную температуру кипения эфира.
Давление пара дихлорметана при 24.1 o C равно 400 Торр, а его энтальпия испарения равна 28.7 кДж . моль –1 . Рассчитать температуру, при которой давление пара будет равно 500 Торр.
Давление пара твердого CO₂ равно 133 Па при –134.3 o C и 2660 Па при –114.4 o C. Рассчитать энтальпию возгонки.
Давление пара (Торр) жидкости в интервале температур 200 – 260 K описывается уравнением:

ln p = 16.255 – 2501.8 / T.

Рассчитать энтальпию испарения и нормальную точку кипения жидкости.

Давление пара (Торр) жидкого бензола C₆H₆ между 10 o C и 80 o C описывается уравнением:

lg p = 7.960 – 1780 / T.
Рассчитать энтальпию испарения и нормальную точку кипения бензола.

Давление пара жидкого нафталина C₁₀H₈ равно 10 Торр при 85.8 o C и 40 Торр при 119.3 o C. Определить энтальпию испарения, нормальную точку кипения и энтропию испарения в нормальной точке кипения.

Нормальная точка кипения гексана равна 69.0єC. Оценить а) мольную энтальпию испарения и б) давление пара гексана при 25єC и 60єC.

При 0 o C энтальпии испарения и плавления воды равны 595 и 79.7 кал . г –1 соответственно. Давление пара воды при 0 o C равно 4.58 мм рт. ст. Рассчитать давление пара льда при –15 o C, считая, что изменение энтальпии не зависит от температуры.

Рассчитать температуру кипения воды на вершине Эвереста (высота 8850 м). Энтальпию испарения воды считать равной 40.67 кДж . моль –1 . Для расчета атмосферного давления на вершине воспользоваться барометрической формулой.

Уксусная кислота имеет следующие давления насыщенного пара:

403P, мм. рт. ст.

Определить молярную массу уксусной кислоты в паре, если известно, что «_испH = 24.35 кДж . моль –1 .

Давление пара (в мм рт. ст.) твердого и жидкого SO₂ выражается уравнениями