Заполните таблицу коэффициентов а в с квадратного уравнения ax2 bx c

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Ваш ответ

Видео:СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать

решение вопроса

Видео:Алгебра 8 класс (Урок№28 - Решение квадратных уравнений вида ax2 + bx + c = 0.Формула корней кв.ур.)Скачать

Похожие вопросы

• Все категории
• экономические 43,401
• гуманитарные 33,632
• юридические 17,905
• школьный раздел 607,977
• разное 16,854

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Квадратичная функция. Построение параболы

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Видео:Квадратные уравнения | Формулы для коэффициентов | АлгебраСкачать

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило, в соответствии с которым каждому значению аргумента соответствует единственное значение функции. Вот какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек координатной плоскости, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Видео:Решаем квадратные уравнения, как?.. Чётный второй коэффициент нам в помощь.Скачать

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0.

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 в частном случае при b = 0, c = 0:

Точки, обозначенные фиолетовыми кружками, называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:

x

y

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов. При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x

y

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля (a > 0), то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля (a 2 + bx + c. Чтобы найти точки пересечения с осью Ox, нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1. Если D 0,то график выглядит так:

1. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
2. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

Теперь понятно, что, зная направление ветвей параболы и знак дискриминанта, мы можем схематично представить график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.

D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

Точка пересечения с осью OY находится: (0; -5) относительно оси симметрии.

Нанесем эти точки на координатную плоскость и построим график параболы:

Видео:коэффициенты в квадратном уравненииСкачать

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀

Зная координаты вершины параболы и старший коэффициент, можно записать уравнение квадратичной функции в виде у = a(x − x₀) + y₀, где x₀, y₀ — координаты вершины параболы.

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.

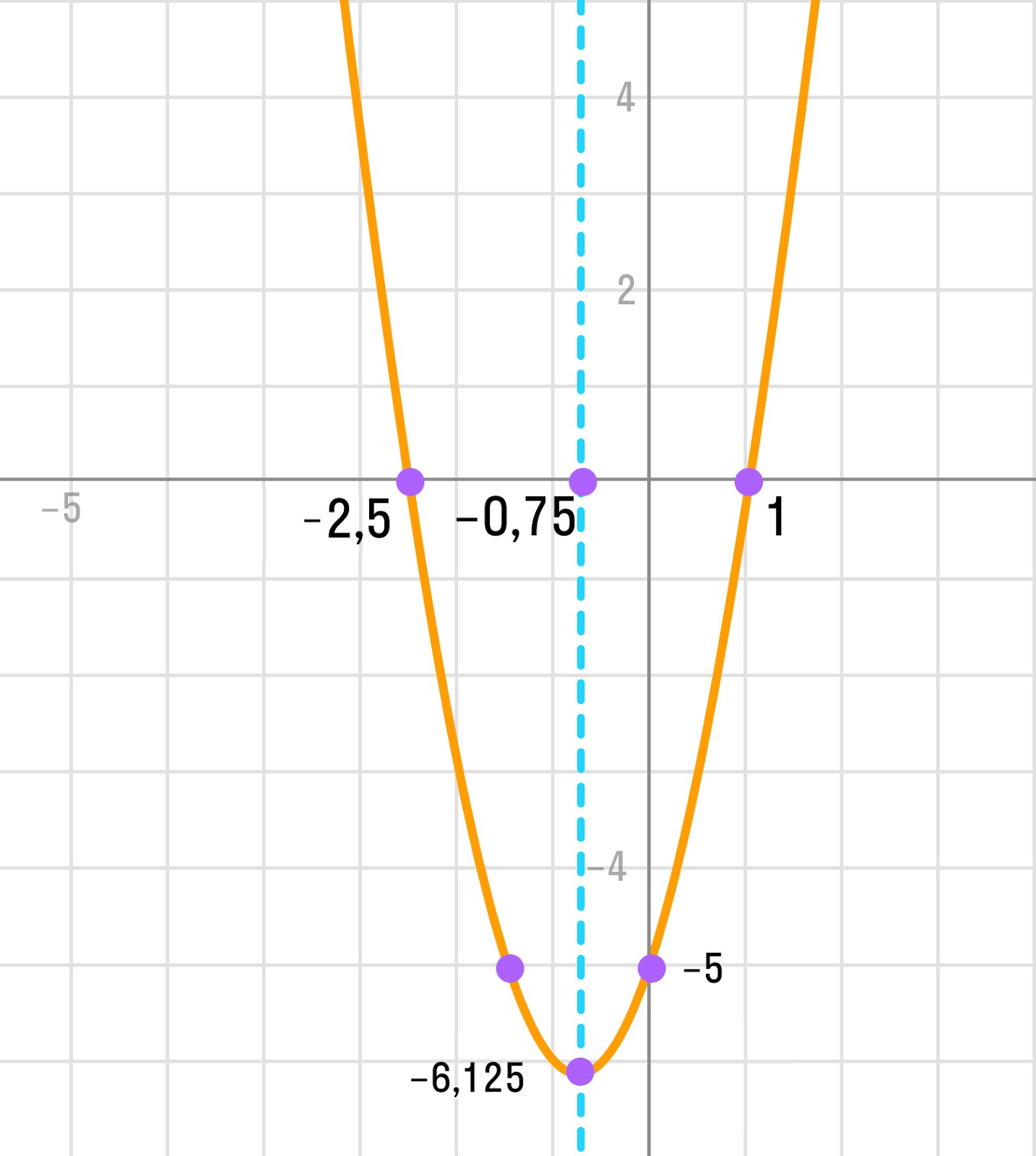
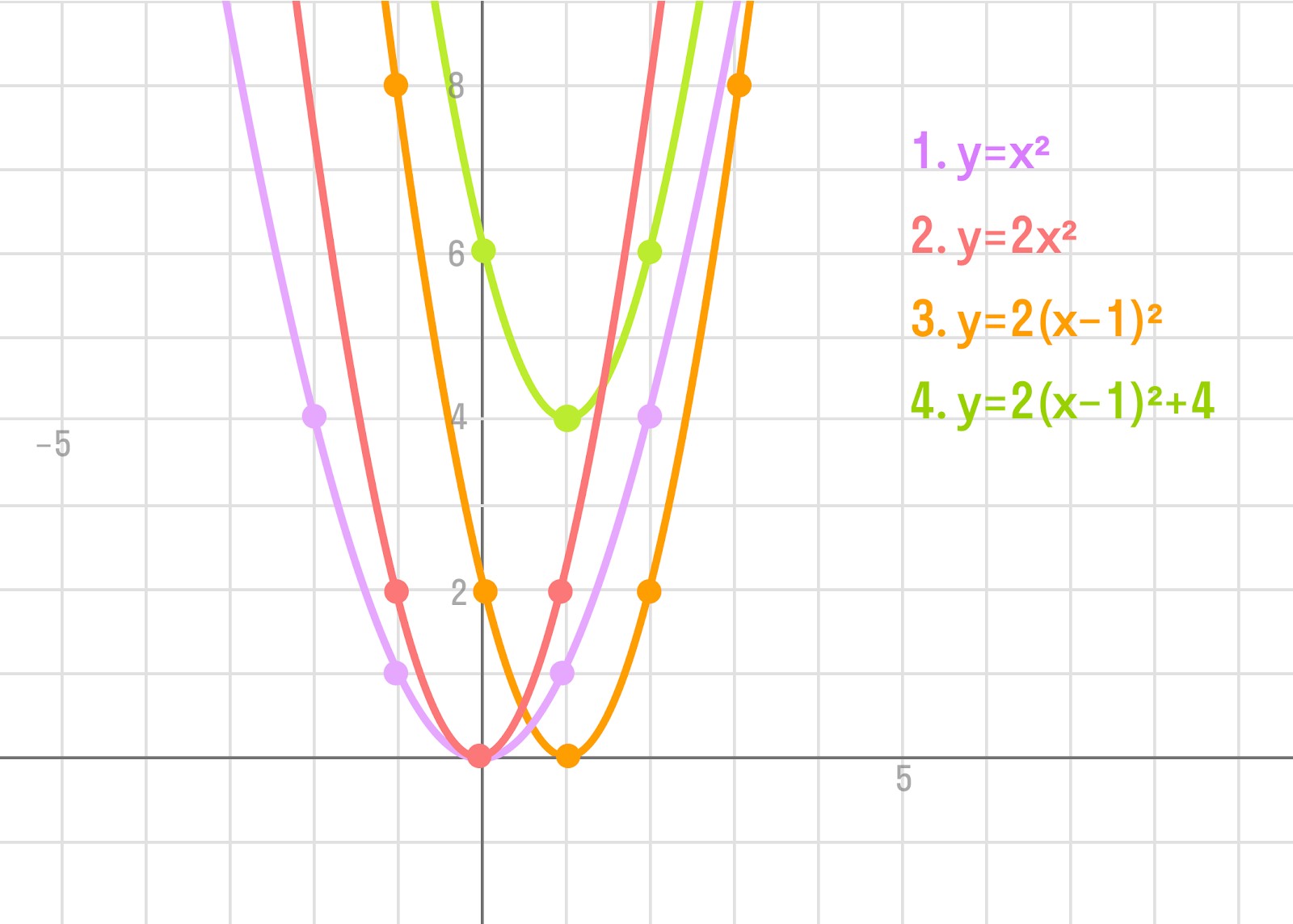
Рассмотрим пример: y = 2 * (x — 1) 2 + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить график функции y = x 2 ,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

Построить график параболы для каждого случая.



Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать



Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид функции позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:



Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная относительно оси симметрии параболы.

Отметим эти точки на координатной плоскости и соединим плавной прямой линией.

Видео:Решение биквадратных уравнений. 8 класс.Скачать



Заполните таблицу коэффициентов а в с квадратного уравнения ax2 bx c

Этот способ решения помогает не только сэкономить время, но и развить внимание.

Дано квадратное уравнение ax 2 + bx + c = 0 . Если a + b + c = 0 (сумма коэффициентов), то



Дано квадратное уравнение ax 2 + bx + c = 0 . Если a — b + c = 0 (сумма коэффициентов), когда b взято с противоположным знаком или a + c = b, то

341x 2 + 290x — 51 = 0

Здесь, a = 341, b = 290, c = -51.

Проверим удовлетворяют ли коэффициенты условию

341 — 51 = 290. Получим а + с = b. Следовательно, мы

можем воспользоваться свойством 2.

Если в квадратном уравнении ax 2 + bx + c = 0 . Коэффициент b представлен в виде 2k, т.е. является четным числом, то формулу корней уравнения можно переписать в более простом виде

📸 Видео

Свойства коэффициентов квадратного уравненияСкачать



Быстрый способ решения квадратного уравненияСкачать



РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ. §19 алгебра 8 классСкачать



Алгебра 8 класс: решение квадратного уравнения с четным коэффициентом b на примере 449.Скачать



Решение квадратных уравнений (урок второй)Скачать



МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?Скачать



СВОЙСТВО КОЭФФИЦИЕНТОВ КВАДРАТНОГО УРАВНЕНИЯСкачать



СВОЙСТВО КОЭФФИЦИЕНТОВ КВАДРАТНОГО УРАВНЕНИЯСкачать



Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать