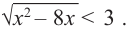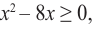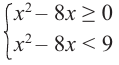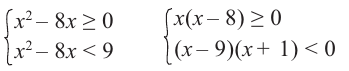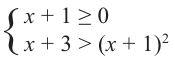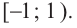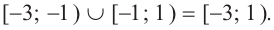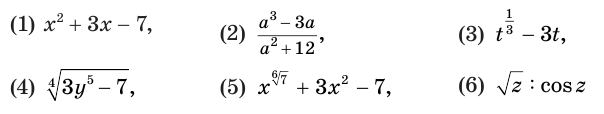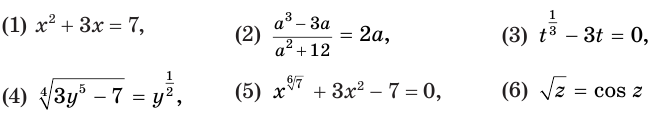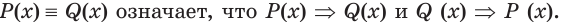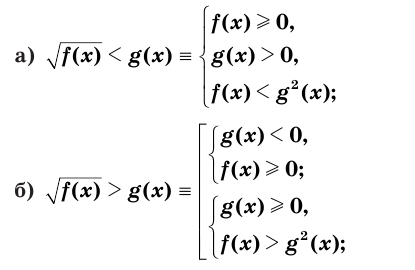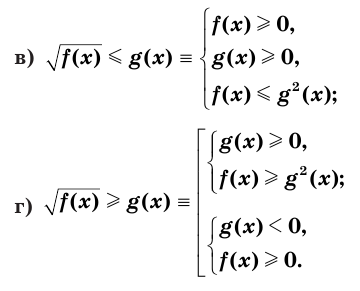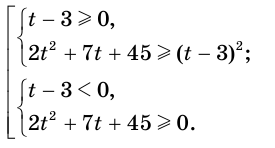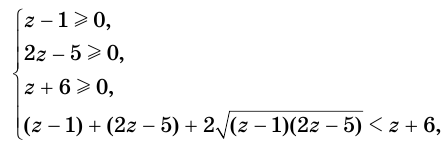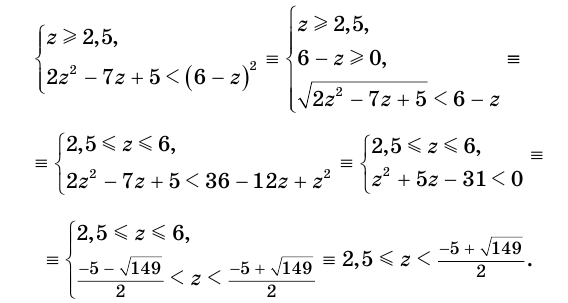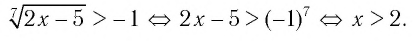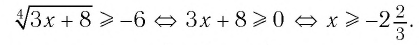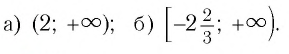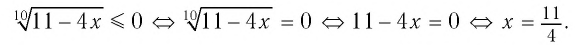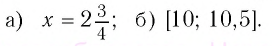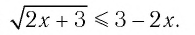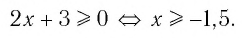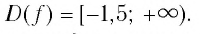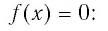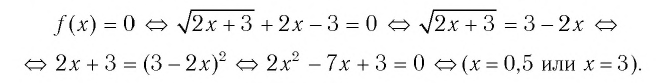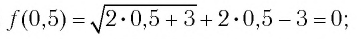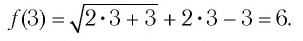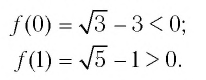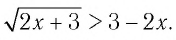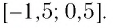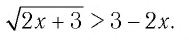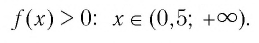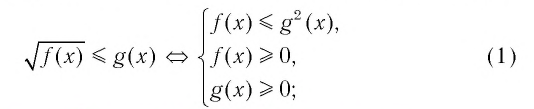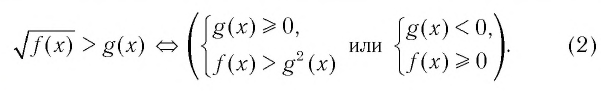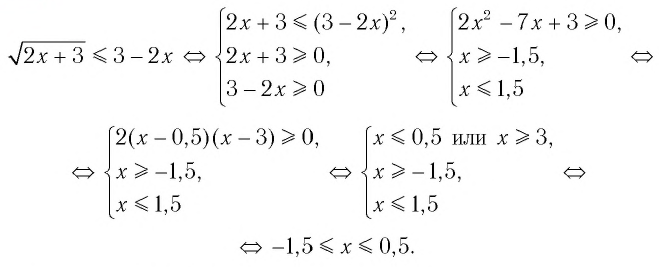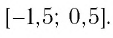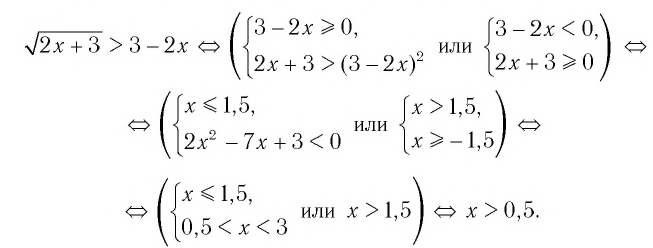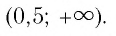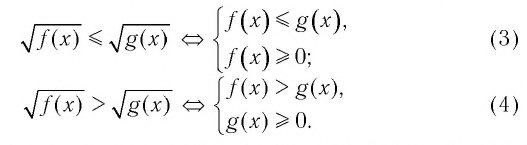Замена неизвестного при решении иррациональных уравнений и неравенств с 14

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Алгебра

Помощь студентам в решении контрольных и курсовых работ

Подготовка к дипломной, повышение уникальности

Помощь студентам в решении контрольных и курсовых работ

Консультация, сбор материала, повышение уникальности

Помощь в подготовке дипломной. Сопровождение до защиты!

План урока:

Видео:ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА неравенства с корнемСкачать

Иррациональные уравнения

Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.

Приведем примеры иррациональных ур-ний:

Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести

Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.

Видео:Замена неизвестного при решении рациональных неравенств.Скачать

Простейшие иррациональные уравнения

Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:

где а – некоторое число (константа), f(x) – рациональное выражение.

Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:

Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии

n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.

Ответ: корней нет.

Пример. Решите ур-ние

Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:

Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).

Пример. Найдите решение ур-ния

Решение. Возведем обе части в пятую степень:

х 2 – 14х – 32 = 0

Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:

D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324

Итак, нашли два корня: (– 2) и 16.

Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.

Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:

х – 2 = х 2 – 8х + 16

D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9

Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):

при х = 3 х – 4 = 3 – 4 = – 1

при х = 6 6 – 4 = 6 – 4 = 2

Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.

Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:

3х 2 + 6х – 25 = (1 – х) 3

3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3

Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:

Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.

Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:

при х = 2 1 – х = 1 – 2 = – 1

Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Видео:Иррациональное неравенство #8Скачать

Уравнения с двумя квадратными корнями

Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.

Пример. Решите ур-ние

Решение. Перенесем вправо один из корней:

Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:

Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:

Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:

(2х – 4) 2 = 13 – 3х

4х 2 – 16х + 16 = 13 – 3х

4х 2 – 13х + 3 = 0

D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121

Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:

Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3

На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.

Видео:Иррациональные неравенства | Математика ЕГЭ | УмскулСкачать

Введение новых переменных

Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние

Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.

Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:

х 1/2 – 10х 1/4 + 9 = 0

Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид

Это квадратное ур-ние. Найдем его корни:

D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64

Получили два значения t. Произведем обратную замену:

х 1/4 = 1 или х 1/4 = 9

Возведем оба ур-ния в четвертую степень:

(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4

х = 1 или х = 6561

Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:

В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.

Пример. Решите ур-ние

х 1/3 + 5х 1/6 – 24 = 0

Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:

Его корни вычислим через дискриминант:

D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121

Далее проводим обратную заменуx 1/6 = t:

х 1/6 = – 8 или х 1/6 = 3

Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.

Видео:Решение уравнения методом замены переменнойСкачать

Замена иррационального уравнения системой

Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.

Пример. Решите ур-ние

Решение. Заменим первый корень буквой u, а второй – буквой v:

Исходное ур-ние примет вид

Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:

Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:

Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:

(х + 6) + (11 – х) = u 3 + v 2

из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:

17 = u 3 + (5 – u) 2

17 = u 3 + u 2 – 10u + 25

u 3 + u 2 – 10u + 8 = 0

Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа

подставим полученные значения в (4):

x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3

x + 6 = 1 или х + 6 = 8 или х + 6 = – 64

х = – 5 или х = 2 или х = – 70

Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим

Корень подошел. Проверяем следующее число, х = 2:

Корень снова оказался верным. Осталась последняя проверка, для х = – 70:

Итак, все три числа прошли проверку.

Видео:Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Уравнения с «вложенными» радикалами

Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:

При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:

Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:

Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:

Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:

Возводим в квадрат и получаем:

х 2 + 40 = (х + 4) 2

х 2 + 40 = х 2 + 8х + 16

И снова нелишней будет проверка полученного корня:

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Иррациональные неравенства

По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:

Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.

Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида

Может быть справедливым только тогда, когда

То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во

при четном n можно заменить системой нер-в

Пример. При каких значениях x справедливо нер-во

Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:

х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)

Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во

чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.

Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.

Пример. Найдите решение нер-ва

Решение. Всё очень просто – надо всего лишь возвести обе части в куб:

x 2 – 7x– 8 2 – 7x– 8 = 0

D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81

Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:

Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.

Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.

Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид

Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.

Пример. Решите нер-во

Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):

И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:

D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9

Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.

стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:

f(x) > 0 (подкоренное выражение не может быть отрицательным);

g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).

Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.

Пример. Решите нер-во

Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим

х 2 – 10х + 21 > 0(1)

Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:

Во-вторых, выражение 4 – х не может быть отрицательным:

Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):

Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:

Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:

Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:

Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:

Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).

Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3

Видео:ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВАСкачать

Решение иррациональных неравенств

Разделы: Математика

1. Общеобразовательная: систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения неравенств.
2. Развивающая: развивать у учащихся умение слушать лекцию, конспективно записывая ее в тетрадь.
3. Воспитательная: формировать познавательную мотивацию к изучению математики.

I. Вводная беседа:

Мы с вами закончили тему “Решение иррациональных уравнений” и сегодня начинаем учиться решать иррациональные неравенства.

Сначала давайте вспомним, какие виды неравенств вы умеете решать и какими методами?

Ответ: Линейные, квадратные, рациональные, тригонометрические. Линейные решаем, исходя из свойств неравенств, тригонометрические сводим к простейшим тригонометрическим, решаемым с помощью тригонометрического круга, а остальные, в основном, методом интервалов.

Вопрос: На каком утверждении основан метод интервалов?

Ответ: На теореме, утверждающей, что непрерывная функция, не обращающаяся в ноль на некотором интервале, сохраняет свой знак на этом интервале.

II. Давайте рассмотрим иррациональное неравенство типа >

Вопрос: Можно ли применить для его решения метод интервалов?

Ответ: Да, так как функция y =– непрерывна на D(y).

Решаем такое неравенство методом интервалов.

Вывод: мы довольно легко решили данное иррациональное неравенство методом интервалов, фактически сведя его к решению иррационального уравнения.

Давайте попробуем решить этим методом другое неравенство.

3) f(x) непрерывна на D(f)

Не будем решать дальше, так как сталкиваемся с вычислительными трудностями:

• Долго искать D(f).
• Трудно вычислять контрольные точки.

Возникает вопрос: “Нет ли других способов решения этого неравенства?”.

Очевидно, есть, и сейчас мы с вами с ними познакомимся.

III. Итак, тема сегодняшнего урока: “Методы решения иррациональных неравенств”.

Урок будет проходить в виде лекции, так как в учебнике нет подробного разбора всех методов. Поэтому наша важная задача: составить подробный конспект этой лекции.

IV. О первом методе решения иррациональных неравенств мы с вами уже поговорили.

Это – метод интервалов, универсальный метод решения всех типов неравенств. Но он не всегда приводит к цели коротким и простым путем.

V. При решении иррациональных неравенств можно использовать те же идеи, что и при решении иррациональных уравнений, но так как простая проверка решений невозможна (ведь решениями неравенств являются чаще всего целые числовые промежутки), то необходимо использовать равносильность.

Приведем схемы решения основных типов иррациональных неравенств методом равносильных переходов от одного неравенства к системе неравенств.

2. Аналогично доказывается, что

Запишем эти схемы на опорной доске. Над доказательствами 3 и 4 типа подумайте дома, на следующем уроке мы их обсудим.

VI. Решим новым способом неравенство.

Исходное неравенство равносильно совокупности систем.

VII. И существует еще третий метод, часто помогающий решать сложные иррациональные неравенства. Мы с вами о нем уже говорили применительно к неравенствам с модулем. Это метод замены функций (замены множителей). Напомню вам, что суть метода замены заключается в том, что разность значений монотонных функций можно заменить разностью значений их аргументов.

Рассмотрим иррациональное неравенство вида b, то неравенства p(a) – p(b) > 0 и a – b > 0 равносильны на D(p), то есть

VIII. Решим методом замены множителей неравенство.

Значит, данное неравенство равносильно системе

Таким образом, мы увидели, что применение метода замены множителей для сведения решения неравенства к методу интервалов существенно сокращает объем работы.

IX. Теперь, когда мы разобрали три основных метода решения уравнений, давайте выполним самостоятельную работу с самопроверкой.

Нужно выполнить следующие номера (по учебнику А. М. Мордковича): 1790(а) – решить _ методом _ равносильныхпереходов, _ 1791(а) – решить методом замены множителей.

Через 10 минут открываем доски с решениями:

X. Подведение итогов:

Вопрос: Какие способы мы рассмотрели для решения иррациональных неравенств?

1. Метод интервалов;
2. равносильные переходы к системе неравенств;
3. метод замены множителей.

XI. Домашнее задание:

1. Оформить конспект лекции в тетради и подумать над доказательствами неравенств 3 и 4 в методе равносильных переходов;
2. Решить методом интервалов неравенство: ;
3. Решить методом равносильных переходов № 1790 (а); № 1792 (в; г);
4. Решить методом замены множителей неравенство: .

На последующих уроках отрабатывается техника решения иррациональных неравенств всеми тремя методами. Учащиеся постепенно сами учатся выбирать наиболее рациональный метод для каждого случая.

Для решения методом равносильных переходов рассматриваются более трудные типы неравенств, например,

Для решения иррациональных неравенств предлагается использовать способы, ранее разобранные при решении иррациональных уравнений:

• замена переменных;
• использование ОДЗ;
• использование свойств монотонности функций.

Завершением изучения темы является контрольная работа.

Анализ контрольной работы показывает:

• типичные ошибки слабых учащихся помимо арифметических и алгебраических – неверные равносильные переходы к системе неравенств;
• метод замены множителей успешно используется только сильными учащимися.

Видео:Иррациональные уравнения — часть 1Скачать

Иррациональные неравенства с примерами решения

Неравенства, содержащие переменную под знаком радикала, называются иррациональными неравенствами.

Содержание:

Решение иррациональных неравенств также ищут на множестве действительных чисел и, используя свойства корня и неравенств, сводится к решению системы рациональных неравенств.

Пример: Решите неравенство

Решение: чтобы найти множество решений данного неравенства на множестве допустимых значений, т. е. при условии

Каждое неравенство системы решим методом интервалов и найдем пересечение полученных решений:

Пример: Решите неравенство

Решение: рассмотрим два случая, в зависимости от знака правой части.

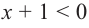
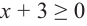
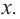
1) при для всех неравенство справедливо для всех Значит, надо решить систему

Ее решением является промежуток

2) при 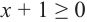обе стороны заданного неравенства можно возвести в квадрат. Тогда получим систему

Ее решением является промежуток

Решением заданного неравенства является

Видео:Решение иррациональных уравнений: метод заменыСкачать

Способы решения иррациональных неравенств

С действием возведения в степень связаны разные виды выражений. Будем рассматривать выражения с переменными, при образовании которых используются действия сложения, вычитания, умножения, деления и возведения в степень, причем возведение в степень хотя бы один раз применено к выражению с переменной.

Если показатель степени целый, то возникает рациональное выражение, если дробный, то — иррациональное выражение, а если иррациональный, то — трансцендентное выражение.

К трансцендентным выражениям приводят и действия нахождения значений синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса, арккотангенса. Рациональные и иррациональные выражения вместе составляют множество алгебраических выражений.

выражения (1) и (2) являются рациональными, выражения (3) и (4) — иррациональными, выражения (5) и (6) — трансцендентными, а выражения (1)—(4) — алгебраическими.

В зависимости от того, из каких выражений составлено уравнение, говорят о рациональных, иррациональных, трансцендентных уравнениях.

уравнения (1) и (2) являются рациональными, уравнения (3) и (4) — иррациональными, а уравнения (5) и (6) — трансцендентными.

Так же говорят о рациональных, иррациональных, трансцендентных неравенствах.

В этом параграфе рассматривается решение иррациональных уравнений и неравенств. При их решении нужно следить за тем, какие преобразования выполняются при этом.

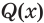
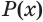
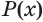
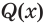
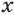
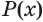
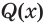
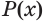
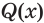
Утверждение равносильно утверждению , если утверждения и истинны при одних и тех же значениях переменной . Равносильность уравнений означает, что они имеют одни и те же корни, а равносильность неравенств — то, что они имеют одни и те же решения. Равносильность утверждений и обозначают = .

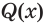
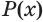
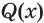
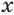
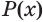
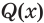
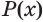
Утверждение следует из утверждения , если утверждение истинно при всех значениях переменной , при которых истинно утверждение . Следование второго уравнения из первого означает, что каждый корень первого уравнения является корнем второго уравнения, но второе уравнение может иметь и дополнительные корни. Так же понимается и следование одного неравенства из другого. Следование утверждения из утверждения обозначают .

Отношения равносильности и следования связаны:

При решении иррациональных неравенств нужно учитывать, что проверка подстановкой найденного множества чисел обычно невозможна из-за его бесконечности. Поэтому при решении неравенств нужно следить за равносильностью проводимых преобразований.

Теорема:

Верны следующие равносильности:

Доказательство проводится по схеме, использованной при доказательстве теоремы 9 с применением соответствующих свойств числовых неравенств.

Пример №1

Решим неравенство 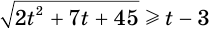. Это неравенство равносильно совокупности неравенств

Первую систему можно заменить равносильной системой 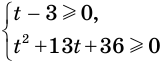, которая равносильна системе , которая, в свою очередь, равносильна неравенству .

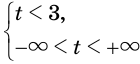
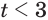
Вторая система совокупности равносильна системе , которая равносильна неравенству .

Решения данного неравенства получим, когда объединим решения и первой и второй систем совокупности, в результате получим множество всех действительных чисел.

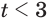
Ответ. .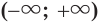

Пример №2

Решим неравенство .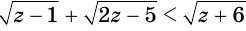

Обратим внимание на то, что на области определения левая и правая части данного неравенства обе неотрицательны, поэтому оно равносильно системе неравенств

решение которой следующее:

Ответ. .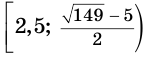

Видео:Иррациональные уравнения и их системы. 11 класс.Скачать

Какие неравенства называются иррациональными

В этой лекции мы будем рассматривать неравенства, содержащие переменную (неизвестное) под знаком корня. Такие неравенства называются иррациональными.

При решении иррациональных неравенств часто используют подход, который мы уже применяли, решая иррациональные уравнения. Он состоит в замене исходного неравенства равносильным ему неравенством (системой или совокупностью неравенств).

Пример №3

Решение:

а) Учитывая свойства корня нечетной степени, получаем:

б) По определению корня четной степени значения выражения

неотрицательны при всех значениях при которых это

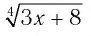
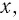
выражение имеет смысл, т. е. когда значения подкоренного выражения неотрицательны. Таким образом, имеем:

Ответ:

Пример №4

Решение:

а) По определению корня четной степени значения выражения 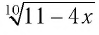отрицательными быть не могут. Поэтому имеем:

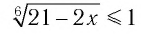
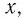
б) Поскольку обе части неравенства неотрицательны при всех значениях при которых его левая часть имеет смысл, то имеем:

Ответ:

При решении иррациональных неравенств часто используется также метод интервалов.

Пример №5

Решить неравенство

Решение:

Обозначим 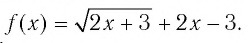Найдем область определения функции

Таким образом,

Найдем нули функции 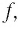т. е. корни уравнения

Проверка:

Значит, 0,5 — единственный нуль функции

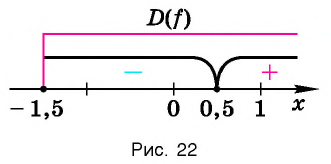
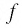
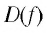
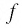
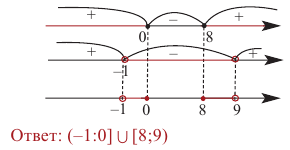
Отметим нуль функции на области определения (рис.22). Определим знаки значений функции на образовавшихся интервалах, для чего вычислим:

Используя рисунок 22, запишем решение неравенства

Ответ:

Пример №6

Решить неравенство

Решение:

Решение этого примера аналогично решению примера 3.

Используя рисунок 22, записываем решение неравенства

Ответ:

▲ При решении иррациональных неравенств часто используются следующие утверждения о равносильности неравенств и систем неравенств:

Решим пример 3, используя равносильность (1):

Ответ:

Решим пример 4, используя равносильность (2):

Ответ:

Для решения заданий такого типа, как, например, в 1.265, можно использовать следующие утверждения о равносильности:

Аналогичные утверждения можно записать и для неравенств

• Производная в математике
• Как найти производную функции
• Асимптоты графика функции
• Касательная к графику функции и производная
• Формулы преобразования суммы и разности синусов (косинусов) в произведение
• Корень n-й степени из числа и его свойства
• Свойства и график функции y=ⁿ√x (n>1, n∈N)
• Иррациональные уравнения

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

📺 Видео

✓ Иррациональное уравнение | ЕГЭ-2018. Задание 12. Математика. Профильный уровень | Борис ТрушинСкачать

8 класс, 38 урок, Иррациональные уравненияСкачать

Это просто! Как решать Показательные Неравенства?Скачать

Иррациональные неравенства. 11 класс.Скачать

Как решать неравенства? Часть 1| МатематикаСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Как решают уравнения в России и СШАСкачать