Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов движений в общем виде.)

1. Вид движения: равнопеременное
2. При сравнении уравнений очевидно, что
- начальный путь, пройденный до начала отсчета – 10 м;
- начальная скорость 20 м/с;
- постоянное касательное ускорение at/2 = 5 м/с ; at= — 10 м/с .
- ускорение отрицательное, следовательно, движение замедленное (равнозамедленное), ускорение направлено в сторону, противоположную направлению скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю:
v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.
Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, график пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).
Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.
Решение
1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).
Нормальное ускорение (ап = v 2 /r) при переходе через точку В увеличивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.
2. На участке ВС:
— касательное ускорение равно нулю: at = 0;
— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение становится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.
3. На участке CD полное ускорение равно нулю.
Пример 3. По заданному графику скорости найти путь, пройденный за время движения (рис. 10.6).
Решение
1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).
Второй участок — равномерное движение: v = 8 м/с; a2 = 0.
Третий участок — торможение до остановки (равнозамедленное движение).
2. Путь, пройденный за время движения, будет равен:
Пример 4. Тело, имевшее начальную скорость 36 км/ч, прошло 50 м до остановки. Считая движение равнозамедленным, определить время торможения.
Решение
1. Записываем уравнение скорости для равнозамедленного движения:
Определяем начальную скорость в м/с: vо = 36*1000/3600 = 10 м/с.
Выразим ускорение (замедление) из уравнения скорости: a = — v0/t
2. Записываем уравнение пути: S = vot/2 + at 2 /2. После подстановки получим: S = vot/2
3. Определяем время до полной остановки (время торможения):
Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t 2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.
Решение
1. Точка движется прямолинейно по уравнению s = 20t – 5t 2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = at = dv/dt = —10 м/с 2 . Значит, движение точки равнопеременное (a = at = —10 м/c 2 = const) с начальной скоростью v0 = 20 м/с.
2. Составим зависимость числовых значений s и v для первых 4 с движения
3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав масштабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Например, если расстояние s = 5 м изображать на графике длиной отрезка ls = 10 мм, то 5м = μs*10мм, где коэффициент пропорциональности μs и есть масштаб по оси Os : μs = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изображать на графике длиной lv =10 мм, то 10 м/c = μv * 10 мм и масштаб по оси Ov μv = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с 2 изображать отрезком la = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μa = 1 м/(с 2 -мм) (1 м/с 2 в 1 мм); и наконец, изображая промежуток времени Δt = 1 с отрезком μt = 10 мм, получим на всех графиках масштаб по осям Ot μt = 0,1 с/мм (0,1 с в 1 мм).
4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сторону).
За 4 с точка прошла путь so_4 = 40 м. Начав движение со скоростью v0 = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.
Если условно принять ускорение свободного падения g = 10 мс 2 и пренебречь сопротивлением воздуха, то можно сказать, что графики описывают движение точки, брошенной вертикально вверх со скоростью а0 = 20 м/с.

Решение
Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, определим из уравнения движения, подставив частные значения расстояния и времени:
Уравнение изменения скорости
Скорость точки в положении 1
Уравнение изменения касательного ускорения
Касательное ускорение точки в положении 1
Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Скорость и ускорение точки в конце этого участка траектории показаны на рис.1.44, б.
Определим скорость и ускорение точки в начале криволинейного участка траектории. Очевидно, что v1 = 11,5 м/с, аt1 = 14,2 м/с 2 .
Нормальное ускорение точки в начале криволинейного участка
Скорость и ускорение в начале криволинейного участка показаны на рис. 1.44, в (векторы at1 и aa1 изображены без соблюдения масштаба).
Положение 2 движущейся точки определяется пройденным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей центральному углу 90°:
Время, необходимое для перемещения точки из положения 0 в положение2,
Скорость точки в положении 2
Касательное ускорение точки в положении 2
Нормальное ускорение точки в положении 2
Ускорение точки в положении 2
Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и аПг изображены без соблюдения масштаба).

Решение
Уравнение изменения скорости
Время t1 определим из уравнения изменения скорости, подставив частные значения скорости и времени:
Определим положение точки на траектории в момент 3 с:
Дуга окружности длиной 135 м соответствует центральному углу
Уравнение изменения касательного ускорения
Касательное ускорение точки в момент tt
Нормальное ускорение точки в момент tt
Ускорение точки в момент tx
Скорость и ускорение точки в момент времени t1 показаны на рис. 1.45, б.
Как видно из рис. 1.45, б
Пример 8. В шахту глубиной H = 3000 м с поверхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверхности земли. Скорость звука 333 м/с.
Решение
Уравнение движения свободно падающего тела
Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравнения движения:
Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука
Время достижения звуком поверхности земли
Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли
Пример 9. По заданным уравнениям движения точки x = 2t 2 , y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и ускорение точки в момент времени t = 2 с.
Решение
Для определения траектории точки нужно из уравнений движения исключить параметр t — время.
Выразим t через х из первого уравнения:
и подставим это значение во второе уравнение:
Траекторией точки является парабола, симметричная относительно оси х.
Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям
Находим скорость точки
При t = 2 с получаем
Находим составляющие ускорения точки
Контрольные вопросы и задания
1. Запишите формулу ускорения при прямолинейном движении.
2. Запишите формулу ускорения (полного) при криволинейном движении.
3. 
4. Параметры движения не меняются.
4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движения точки, ответьте, чему равны начальная скорость и ускорение.
5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.
6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).
7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).
 |
8. Ответьте на вопросы тестового задания.
Темы 1.7, 1.8. Кинематика. Кинематика точки
 |
.
ЛЕКЦИЯ 11
Дата добавления: 2017-09-01 ; просмотров: 10632 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Решение графических задач на равномерное движениеСкачать

Примеры решения задач. Пример 1. По заданному закону движения S =10 + 20t — 5t2 ([S] = м; [t] = с) определить вид движения
Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов движений в общем виде.)

1. Вид движения: равнопеременное
2. При сравнении уравнений очевидно, что
- начальный путь, пройденный до начала отсчета – 10 м;
- начальная скорость 20 м/с;
- постоянное касательное ускорение at/2 = 5 м/с ; at= — 10 м/с .
- ускорение отрицательное, следовательно, движение замедленное (равнозамедленное), ускорение направлено в сторону, противоположную направлению скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю:
v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.
Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, график пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).
Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.
Дата добавления: 2015-09-07 ; просмотров: 2079 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Урок математики по теме «Применение интеграла к решению физических задач»
Презентация к уроку
Цель урока:
- обобщить и закрепить ключевые задачи по теме;
- научиться работать с теоретическими вопросами темы;
- научиться применять интеграл к решению физических задач.
План урока:
1. Схема решения задач на приложения определенного интеграла
2. Нахождение пути, пройденного телом при прямолинейном движении
3. Вычисление работы силы, произведенной при прямолинейном движении тела
4. Вычисление работы, затраченной на растяжение или сжатие пружины
5. Определение силы давления жидкости на вертикально расположенную пластинку
Тип урока: интегрированный.
Воспитательная работа: расширение кругозора и познавательной деятельности учащихся, развитие логического мышления и умения применять свои знания.
Техническое обеспечение: интерактивная доска. Компьютер и диск.
Приложение: «Рапсодия природы».
I. Организационный момент
II. Постановка цели урока
– Урок хотелось бы провести под девизом Готфрида Вильгельма Лейбница – немецкого философа, логика, математика, физика: «Общее искусство знаков представляет чудесное пособие, так как оно разгружает воображение… Следует заботиться о том, чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли».
III. Повторим основные понятия и ответим на вопросы:
– Скажите основное определение интеграла?
– Что вы знаете о интеграле (свойства, теоремы)?
– Знаете ли вы какие-нибудь примеры задач с применением интеграла?
IV. Объяснение нового материала (рассмотрение теории):
1. Схема решения задач на приложения определенного интеграла
С помощью определенного интеграла можно решать различные задачи физики, механики и т. д., которые трудно или невозможно решить методами элементарной математики.
Так, понятие определенного интеграла применяется при решении задач на вычисление работы переменной силы, давления жидкости на вертикальную поверхность, пути, пройденного телом, имеющим переменную скорость, и ряд других.
Несмотря на разнообразие этих задач, они объединяются одной и той же схемой рассуждений при их решении. Искомая величина (путь, работа, давление и т. д.) соответствует некоторому промежутку изменения переменной величины, которая является переменной интегрирования. Эту переменную величину обозначают через Х, а промежуток ее изменения – через [а, b].
Отрезок [a, b] разбивают на n равных частей, в каждой из которых можно пренебречь изменением переменной величины. Этого можно добиться при увеличении числа разбиений отрезка. На каждой такой части задачу решают по формулам для постоянных величин.
Далее составляют сумму (интегральную сумму), выражающую приближенное значение искомой величины. Переходя к пределу при 
I = 
2. Нахождение пути, пройденного телом при прямолинейном движении
Как известно, путь, пройденный телом при равномерном движении за время t, вычисляется по формуле S = vt.
Если тело движется неравномерно в одном направлении и скорость его меняется в зависимости от времени t, т. е. v = f(t), то для нахождения пути, пройденного телом за время от 



Если функция v(t) непрерывна, то
Итак,
3. Вычисление работы силы, произведенной при прямолинейном движении тела
Пусть тело под действием силы F движется по прямой s, а направление силы совпадает с направлением движения. Необходимо найти работу, произведенную силой F при перемещении тела из положения a в положение b.
Если сила F постоянна, то работа находится по формуле 
Пусть на тело, движущееся по прямой Ох, действует сила F, которая изменяется в зависимости от пройденного пути, т. е. 


Составим интегральную сумму, которая приближенно равна значению произведенной работы:
т.е. работа, совершенная этой силой на участке от а до b, приближенно мала сумме:
Итак, работа переменной силы вычисляется по формуле:
4. Вычисление работы, затраченной на растяжение или сжатие пружины
Согласно закону Гука, сила F, необходимая для растяжения или сжатия пружины, пропорциональна величине растяжения или сжатия.
Пусть х – величина растяжения или сжатия пружины. Тогда 
Работа на участке 




Для нахождения истинной величины работы следует перейти к пределу
5. Определение силы давления жидкости на вертикально расположенную пластинку
Из физики известно, что сила Р давления жидкости на горизонтально расположенную площадку S, глубина погружения которой равна h, определяется по формуле:
, где
– плотность жидкости.
Выведем формулу для вычисления силы давления жидкости на вертикально расположенную пластинку произвольной формы, если ее верхний край погружен на глубину a, а нижний – на глубину b.
Так как различные части вертикальной пластинки находятся на разной глубине, то сила давления жидкости на них неодинаковa. Для вывода формулы нужно разделить пластинку на горизонтальных полос одинаковой высоты 
По закону Паскаля сила давления жидкости на такую полосу равна силе движения жидкости на горизонтально расположенную пластинку той же площади, погруженной на ту же глубину.
Тогда согласно формуле (4) сила давления на полосу, находящуюся на расстоянии х от поверхности, составит 

Составим интегральную сумму и найдем ее предел, равный силе давления жидкости на всю пластинку:
Если верхний край пластинки совпадает с поверхностью жидкости, то а=0 и формула (5) примет вид
Ширина каждой полосы зависит от формы пластинки и является функцией глубины х погружения данной полосы.
Для пластинки постоянной ширины формула (5) упрощается, т.к. эту постоянную можно вынести за знак интеграла:
V. Разбор задач по теме
1) Скорость движения материальной точки задается формулой 

2) Скорость движения изменяется по закону 
3) Скорость движения тела задана уравнением 
Скорость движение тела равна нулю в момент начала его движения и остановки. Найдем момент остановки тела, для чего приравняем скорость нулю и решим уравнение относительно t; получим
4) Тело брошено вертикально вверх со скоростью, которая изменяется по закону 
Найдем время, в течении которого тело поднималось вверх: 29,4–9,8t=0 (в момент наибольшего подъема скорость равна нулю); t = 3 с. Поэтому
5) Какую работу совершает сила в 10Н при растяжении пружины на 2 см?
По закону Гука сила F, растягивающая пружину, пропорциональна растяжению пружины , т.е. F = kx. Используя условие, находим 
6) Сила в 60Н растягивает пружину на 2 см. Первоначальная длина пружины равна 14 см. Какую работу нужно совершить, чтобы растянуть ее до 20 см?
Имеем 
7) Определить силу давления воды на стенку шлюза, длина которого 20 м, а высота 5 м (считая шлюз доверху заполненным водой).
Здесь y = f(x) = 20, a = 0, b = 5 м, 

8) В воду опущена прямоугольная пластинка, расположенная вертикально. Ее горизонтальная сторона равна 1 м, вертикальная 2 м. Верхняя сторона находится на глубине 0,5 м. Определить силу давления воды на пластинку.
Здесь y = 1, a = 0,5, b = 2 + 0,5 = 2,5 (м), 

9) Скорость прямолинейного движения точки задана уравнением 
Известно, что скорость прямолинейного движения тела равна производной пути s по времени t, т.е. 
Это искомое уравнение.
10) Скорость тела задана уравнением 


Имеем ds = v dt = (6
Подставив в найденное уравнение начальные условия s = 60 м, t = 3 c, получим

Искомое уравнение примет вид
11) Тело движется со скоростью 
Так как ds = v dt = (
Из условия следует, что если t = 0, то s = 5 см = 0,05 м. подставив эти данные в полученное уравнение, имеем 
Тогда искомое уравнение примет вид
12) Вычислить силу давления воды на плотину, имеющую форму трапеции, у которой верхнее основание, совпадающее с поверхностью воды, имеет длину 10 м, нижнее основание 20 м, а высота 3 м.
13) Цилиндрический стакан наполнен ртутью. Вычислить силу давления ртути на боковую поверхность стакана, если его высота 0,1 м, а радиус основания 0,04 м. Плотность ртути равна 13600 кг/
Вычислим площадь круглой полоски
Элементарная сила давления составляет
VI. Самостоятельное решение задач на доске, коллективный разбор решений задач:
- Скорость движения тела задана уравнением
. Найти уравнение движения, если в начальный момент времени
- Найти уравнение движения точки, если к моменту начала отсчета она прошла путь
, а его скорость задана уравнением
- Скорость движения тела пропорциональна квадрату времени. Найти уравнение движения тела, если известно, что за 3 с оно прошло 18 м.
- Тело движется прямолинейно со скоростью
м/с. Найти путь, пройденный телом за 5 с от начала движения.
- Скорость движения тела изменяется по закону
м/с. Найти путь, пройденный телом за 4 с от начала движения.
- Найти путь пройденный телом за 10-ю секунду, зная, что что скорость его прямолинейного движения выражается формулой
м/с.
- Найти путь, пройденный точкой от начала движения до ее остановки, если скорость ее прямолинейного движения изменяется по закону
м/с.
- Какую работу совершает сила в 8 Н при растяжении пружины на 6 см?
- Сила в 40 Н растягивает пружину на 0,04 м. Какую работу надо совершить, чтобы растянуть пружину на 0,02 м?
- Вычислить силу давления воды на вертикальную прямоугольную пластинку, основание которой 30 м, а высота 10 м, причем верхний конец пластинки совпадает с уровнем воды.
- Вычислить силу давления воды на одну из стенок аквариума, имеющего длину 30 см и высоту 20 см.
VII. Минутка релаксации
VIII. Подведение итогов урока:
– Каким вопросам был посвящен урок?
– Чему научились на уроке?
– Какие теоретические факты обобщались на уроке?
– Какие рассмотренные задачи оказались наиболее сложными? Почему?
Список литературы:
- Журнал «Потенциал»
- «Алгебра и начала анализа» 11 класс С.М. Никольский, М.К. Потапов и др.
- «Алгебра и математический анализ» Н.Я. Виленкин и др.
- «Учебник по математическому анализу» Град О.Г., Змеев О.А.
- «Высшая математика: Учебник для вузов». В 3 томах. Бугров Я.С. Никольский С.М.
- «Математический анализ». Е.Б. Боронина
📹 Видео
Задача из ЕГЭ по физике │Анализ графика #1Скачать

Урок 15. Решение задач на графики движенияСкачать

Способы описания движения. Траектория. Путь. ПеремещениеСкачать

Задачи на движение. Учимся решать задачи на движение. Способы решения задач на движение.Скачать

Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Графики зависимости пути и скорости от времениСкачать

10 класс. Физика. Прямолинейное равномерное движениеСкачать

Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Урок 19 (осн). Задачи на график движенияСкачать
ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Математика 5 класс (Урок№35 - Задачи на движение.)Скачать

Физика - уравнения равноускоренного движенияСкачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Урок 16 (осн) Средняя скорость. Вычисление пути и времени движенияСкачать

Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Кинематика. Закон движения. Урок 3Скачать

Свободное падение тел. 10 класс.Скачать

Способы описания движения Система отсчётаСкачать


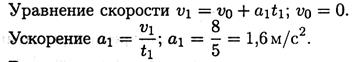
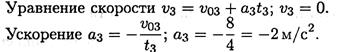
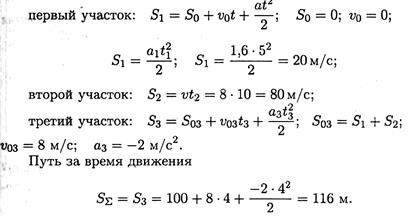

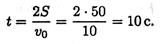

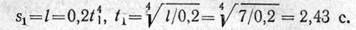
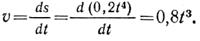
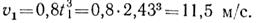
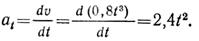
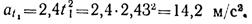
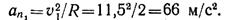
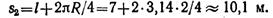
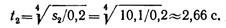
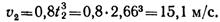
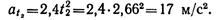
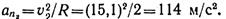
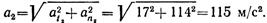
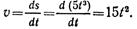
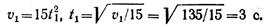
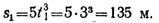
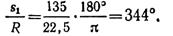
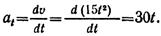
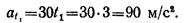
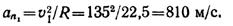
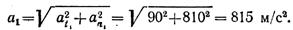
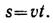
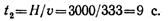
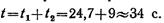
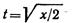
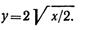
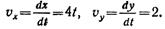
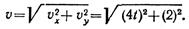
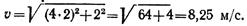
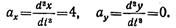
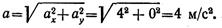










 , где
, где  – плотность жидкости.
– плотность жидкости.






















 . Найти уравнение движения, если в начальный момент времени
. Найти уравнение движения, если в начальный момент времени 
 , а его скорость задана уравнением
, а его скорость задана уравнением 
 м/с. Найти путь, пройденный телом за 5 с от начала движения.
м/с. Найти путь, пройденный телом за 5 с от начала движения. м/с. Найти путь, пройденный телом за 4 с от начала движения.
м/с. Найти путь, пройденный телом за 4 с от начала движения. м/с.
м/с. м/с.
м/с.