- Примеры решения задач «Логические основы работы компьютера»
- Логические схемы и таблицы истинности
- Задача анализа логических схем
- Найти булеву функцию логической схемы самостоятельно, а затем посмотреть решение
- Продолжаем искать булеву функцию логической схемы вместе
- Задача синтеза логических схем в булевом базисе
- Задача синтеза логических схем в базисах «И-НЕ» и «ИЛИ-НЕ»
- Решение задач «Базовые логические элементы»
- Логические схемы. Решение задач.
- Просмотр содержимого документа «Логические схемы. Решение задач.»
- 🎬 Видео
Видео:Логические выражения, таблицы истинности ,структурная логическая схемаСкачать

Примеры решения задач «Логические основы работы компьютера»
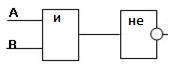
Дана логическая функция: F (А,В) = ¬ (А / В). Постройте соответствующую ей функциональную схему.
Функциональная схема будет содержать 2 входа А и В. Рассмотрим логическое выражение и определим порядок действий в нем:
1) первым выполняется логическое умножение А / В, следовательно, сигналы с входов А и В подаются на конъюнктор;
2) далее выполняется логическое отрицание ¬(А / В), следовательно, сигнал, полученный на выходе из конъюнктора должен быть инвертирован, т.е. подан на инвертор.
Выход инвертора является выходом функциональной схемы.
Изобразим схему, следуя данным действиям:
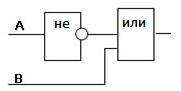
Определите логическую функцию, соответствующую заданной функциональной схеме:
Решение:
Функциональная схема содержит 2 входа А и В. Вход А инвертирован и его выход является входом дизъюнктора. Вход В подает сигнал на дизъюнктор. Выход дизъюнктора является выходом функциональной схемы.
Итак, последовательность действий:
1) ¬A — сигнал входа А инвертирован;
2) ¬A / B — на дизъюнктор подают инвертированный сигнал входа А и нормальный входа В.
Выход дизъюнктора является выходом функциональной схемы. Следовательно, логическая функция F –это функция двух переменных А и В и имеет вид:
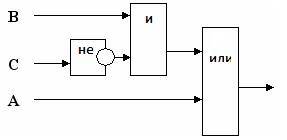
Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F=A/B/ ¬C, если А=1, В=1, С=1.
Значение логического выражения — 1
Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F= ¬(A/B/C),если А=0, В=1, С=1.
Видео:ЕГЭ информатика. Пример решения заданий. Таблицы истинности и логические схемыСкачать

Логические схемы и таблицы истинности
Логические схемы создаются для реализации в цифровых устройствах булевых функций (функций алгебры логики).
В цифровой схемотехнике цифровой сигнал — это сигнал, который может принимать два значения, рассматриваемые как логическая «1» и логический «0».
Логические схемы могут содержать до 100 миллионов входов и такие гигантские схемы существуют. Представьте себе, что булева функция (уравнение) такой схемы была потеряна. Как восстановить её с наименьшими потерями времени и без ошибок? Наиболее продуктивный способ — разбить схему на ярусы. При таком способе записывается выходная функция каждого элемента в предыдущем ярусе и подставляется на соответствующий вход на следующем ярусе. Этот способ анализа логических схем со всеми нюансами мы сегодня и рассмотрим.
Логические схемы реализуются на логических элементах: «НЕ», «И», «ИЛИ», «И-НЕ», «ИЛИ-НЕ», «Исключающее ИЛИ» и «Эквивалентность». Первые три логических элемента позволяют реализовать любую, сколь угодно сложную логическую функцию в булевом базисе. Мы будем решать задачи на логические схемы, реализованные именно в булевом базисе.
Для обозначения логических элементов используется несколько стандартов. Наиболее распространёнными являются американский (ANSI), европейский (DIN), международный (IEC) и российский (ГОСТ). На рисунке ниже приведены обозначения логических элементов в этих стандартах (для увеличения можно нажать на рисунок левой кнопкой мыши).
На этом уроке будем решать задачи на логические схемы, на которых логические элементы обозначены в стандарте ГОСТ.
Задачи на логические схемы бывают двух видов: задача синтеза логических схемы и задачи анализа логических схем. Мы начнём с задачи второго типа, так как в таком порядке удаётся быстрее научиться читать логические схемы.
Чаще всего в связи с построением логических схем рассматриваются функции алгебры логики:
- трёх переменных (будут рассмотрены в задачах анализа и в одной задаче синтеза);
- четырёх переменных (в задачах синтеза, то есть в двух последних параграфах).
Рассмотрим построение (синтез) логических схем
- в булевом базисе «И», «ИЛИ», «НЕ» (в предпоследнем параграфе);
- в также распространённых базисах «И-НЕ» и «ИЛИ-НЕ» (в последнем параграфе).
Логические схемы строятся на основе логических выражений и функций. Бывает, что изначально составленная функция является излишне сложной, из-за чего её схемная или программная реализация оказывается избыточной. Способам и приёмам минимизации логических функций посвящены отдельные материалы сайта — минимизация логических функций: общие сведения, минимизация логических функций: метод непосредственных преобразований и минимизация логических функций: метод Квайна.
Видео:Построение схем по логическим выражениямСкачать

Задача анализа логических схем
Задача анализа заключается в определении функции f , реализуемой заданной логической схемой. При решении такой задачи удобно придерживаться следующей последовательности действий.
- Логическая схема разбивается на ярусы. Ярусам присваиваются последовательные номера.
- Выводы каждого логического элемента обозначаются названием искомой функции, снабжённым цифровым индексом, где первая цифра — номер яруса, а остальные цифры — порядковый номер элемента в ярусе.
- Для каждого элемента записывается аналитическое выражение, связывающее его выходную функцию с входными переменными. Выражение определяется логической функцией, реализуемой данным логическим элементом.
- Производится подстановка одних выходных функций через другие, пока не получится булева функция, выраженная через входные переменные.
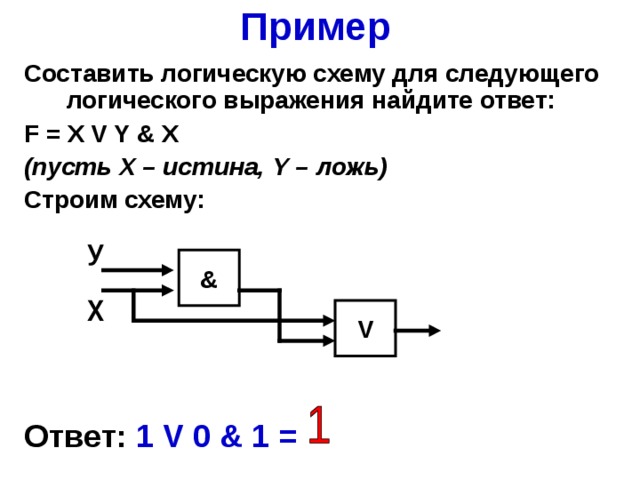
Пример 1. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.
Решение. Разбиваем логическую схему на ярусы, что уже показано на рисунке. Запишем все функции, начиная с 1-го яруса:
Теперь запишем все функции, подставляя входные переменные x, y, z :
В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:
| x | y | z |  |  |  |  | f |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
Видео:Конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание. На примерах из жизни. Логика.Скачать

Найти булеву функцию логической схемы самостоятельно, а затем посмотреть решение
Пример 2. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.
Пример 3. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.
Видео:Построение таблиц истинностиСкачать

Продолжаем искать булеву функцию логической схемы вместе
Пример 4. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.
Решение. Разбиваем логическую схему на ярусы. Запишем все функции, начиная с 1-го яруса:
Теперь запишем все функции, подставляя входные переменные x, y, z :
В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:
| x | y | z |  |  | f |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 |
Пример 5. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.
Решение. Разбиваем логическую схему на ярусы. Структура данной логической схемы, в отличие от предыдущих примеров, имеет 5 ярусов, а не 4. Но одна входная переменная — самая нижняя — пробегает все ярусы и напрямую входит в логический элемент в первом ярусе. Запишем все функции, начиная с 1-го яруса:
Теперь запишем все функции, подставляя входные переменные x, y, z :
В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:
| x | y | z |  |  | f |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 1 |
Видео:Разбор построение логических схемСкачать
Задача синтеза логических схем в булевом базисе
Разработка логической схемы по её аналитическому описанию имеет название задачи синтеза логической схемы.
Каждой дизъюнкции (логической сумме) соответствует элемент «ИЛИ», число входов которого определяется количеством переменных в дизъюнкции. Каждой конъюнкции (логическому произведению) соответствует элемент «И», число входов которого определяется количеством переменных в конъюнкции. Каждому отрицанию (инверсии) соответствует элемент «НЕ».
Часто разработка логической схемы начинается с определения логической функции, которую должна реализовать логическая схемы. В этом случае дана только таблица истинности логической схемы. Мы разберём именно такой пример, то есть, решим задачу, полностью обратную рассмотренной выше задаче анализа логических схем.
Пример 6. Построить логическую схему, реализующую функцию с данной таблицей истинности:
| x | y | f |
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Разбираем таблицу истинности для логической схемы. Определяем функцию, которая получится на выходе схемы и промежуточные функции, которые на входе принимают аргументы x и y . В первой строке результатом реализации выходной функции при том, что значения входных переменных равны единицам, должен быть логический «0», во второй строке — при разных значениях входных переменных на выходе тоже должен быть логический «0». Поэтому нужно, чтобы выходная функция была конъюнкцией (логическим произведением).
Теперь подбираем промежуточные функции. Получаем следующую таблицу для промежуточных функций и выходной функции — конъюнкции промежуточных функций:
 |  |  |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
Для построения логической схемы необходимо элементы, реализующие логические операции, указанные в выходной функции, располагать в порядке, заданной этой функцией. Из выражения видно, что понадобятся 3 схемы «НЕ», две двухвходовых схемы «И» и одна двухвходовая схема «ИЛИ». В соответствии с выходной функцией 
А теперь очередь дошла до функций алгебры логики четырёх переменных. Сначала выполним синтез логической схемы в булевом базисе.
Пример 7. Построить в булевом базисе логическую схему, реализующую функцию алгебры логики
Решение. Для построения логической схемы потребуются 4 схемы «НЕ», одна трёхвходовая схема «И», 2 двухвходовые схемы «И» и одна трёхвходовая схема «ИЛИ». В соответствии с этим получаем следующую логическую схему:
Видео:ЕГЭ по информатике - Задание 2 (Мощнейший метод!)Скачать

Задача синтеза логических схем в базисах «И-НЕ» и «ИЛИ-НЕ»
Часто для сокращения числа микросхем используют элементы «И-НЕ» или/и «ИЛИ-НЕ». Рассмтрим примеры, как построить схему, реализующую ту же функцию, что в предыдущем примере, но, сначала в базисе «И-НЕ», а затем в базисе «ИЛИ-НЕ».
Пример 8. Построить в базисе «И-НЕ» логическую схему, реализующую функцию алгебры логики 
Решение. Логическая функция должна быть приведена к виду, содержащему только операции логического умножения (конъюнкции) и инвертирования (отрицания). Это делается при помощи двойного инвертирования исходного выражения функции и применения закона де Моргана:
Для построения логической схемы потребуются 8 схем «И-НЕ». Получаем следующую логическую схему:
Пример 9. Построить в базисе «ИЛИ-НЕ» логическую схему, реализующую функцию алгебры логики 
Видео:Таблица истинностиСкачать

Решение задач «Базовые логические элементы»
- отработать навыки построения функциональных схем, записи логических функций
- сформировать навыки построения однотактных автоматов,
- научиться синтезировать логические схемы
- воспитание познавательного интереса учащихся, умения слушать, аккуратности в работе, трудолюбия, умения работать в группах.
- формирование интеллектуальной и эмоциональной активности учащихся.
- становление и развитие логического мышления:
- развитие познавательного интереса:
- формирование информационной культуры и потребности приобретения знаний.
- развитие конструкторских умений,
- формирование элементов графической культуры;
- восприятие компьютера, как инструмента, работающего по законам логики
Поминутный план урока: см. Приложение 1 (“План урока.doc”)
Ход всего урока сопровождается показом презентации “Логические основы компьютера.ppt” (см. Приложение 2)
Перед началом урока на компьютерах учащихся должен быть размещен необходимый материал для работы: папки “Задание для работы в группах ,,Алмазы,, и “Дополнительное задание для самостоятельной работы”; файл “Задания для самостоятельной работы.doc” (см. Приложение 3).
I. Организационный момент. Постановка целей урока
– На предыдущем уроке мы с вами познакомились с основами базовых логических элементов, с построением логических схем и даже пытались решать простейшие задания, основанные на построении логических схем по заданной формуле.
Цели нашего сегодняшнего урока:
- закрепить навыки построения функциональных схем и записи логических функций;
- а так же научиться синтезировать логические схемы, т.е. попытаемся научиться применять полученные знания для построения более сложных схем и решения практических задач.
– Но, прежде, чем мы приступим к основной работе, давайте повторим основный теоретические момент, изученные на предыдущем уроке.
II. Проверка домашнего задания
– При ответе на вопросы вам надо будет либо записать на листке пропущенное слово (или несколько слов), либо указать через запятую номера правильных, как вы считаете, ответов. В некоторых вопросах правильный ответ – единственно верный, а в некоторых – их несколько. Время на выполнение ограничено. Подпишите, пожалуйста, листочки … и приступим….
Задания теста на слайдах презентации к уроку. По окончании тестирования, собрать листочки.
III. Разделение на группы и объяснение задачи.
– Вы прекрасно понимаете, что строя электрические цепи можно обмотать весь дом проводами и не добиться нужного эффекта, а можно, используя минимальное число элементов и соединений добиться задуманного. Стоит только задуматься и выбрать правильное решение.
“Всё наше достоинство заключено в мысли
Не пространство, не время, которые мы не можем заполнить,
возвышает нас, а именно она, наша мысль.
Будем же учиться хорошо мыслить.”
Французский математик и философ XVII века Б.Паскаль
Задача заключается в том, чтобы последовательно передавать алмаз с верхней площадки на нижнюю. Подавая ток на вход механизмов в правой части схемы, можно выдвигать площадки на пути алмаза. Если на входе механизма нет тока, площадка убирается.
- Для управления механизмами используют выключатели в левой части поля. Их состояние изменяется щелчком мыши. Если выключатель включен, по цепи идет ток и поступает на логические схемы, включенные в эту цепь (средняя часть поля). Логические схемы различны: инвертор, конъюнктор и т.д.
Алмаз нельзя передавать сразу через несколько «пролетов» – в этом случае он разбивается и приходится начинать уровень заново. Кроме того, у вас есть только 5 алмазов на всю игру, если вы разобьете их все, задание считается невыполненным. Придется начинать с самого начала – с первого уровня.
Игра состоит из 10 уровней. На все отводится 4 минуты. Ваша задача – пройти на более высокий уровень. Я призываю вас не жать на выключатели бездумно, а, действительно, пытаться “хорошо мыслить”. Начинаем.
IV. Работа в группах (алмаз).
Задание: см. Приложение 4 (папка “Задание для работы в группах ,,Алмазы,,).
Выполнение задания на компьютерах (работа в парах). На работу 4 минуты.
– Поднимите руки те команды, которые смогли подняться выше 6-го уровня. (Выставление оценок.)
V. Работа в группах (задания по схемам).
Класс разбивается на группы по 4 человека для работы в группах по схемам.
Цель работы: при выполнении заданий продумать и сформулировать алгоритм для решения задач подобного типа.
– По окончании работы представитель группы будет защищать решение перед классом. На всю работу 6 минут.
Через 5 минут после начала работы зазвучит музыка. Предупредить учащихся, что время для выполнения работы подходит к концу и пора заканчивать. Через 1,5 минуты все учащиеся рассаживаются на места.
VI. Физкультминутка (1 минута (до окончания музыки)).
VII. “Выступление” представителей групп.
Решение заданий для групп: см. Приложение 6 (“Решение заданий для групп.doc”).
1-я группа: объясняет решение задания № 1.
2-я группа: объясняет алгоритм решения задач, подобных заданию № 1.
3-я группа: объясняет решение задания № 2.
4-я группа: объясняет алгоритм решения задач, подобных заданию № 2.
На защиту решений каждой группе дается 1, 5 минуты.
VIII. Решение задачи “Синтез автоматов”.
Объяснение нового материала учителем: совместная работа учащихся и учителя.
Конструирование (синтез) автоматов – одна из основных задач кибернетики.
(Кибернетика – наука о процессах управления в сложных динамических системах, основывающаяся на теоретическом фундаменте математики и логики, а также применении ВТ.)
Автомат – агрегат, представляющий собой систему механизмов и устройств, в которой полностью механизированы, т.е. выполняются без непосредственного участия человека, процессы получения, преобразования, передачи и использования энергии, вещества или информации.
Алгоритм синтеза автоматов 
Рис. 1
Задача 1. Для оповещения зрителей, наблюдающих за ходом состязаний по тяжелой атлетике, изготовлен светящийся транспарант: “Вес взят правильно”. Подсвечивание транспаранта осуществляется по команде, выдаваемой автоматом. Этот автомат обрабатывает сигналы, поступающие от трех судей А, В, С. Судья А – старший. Сигнал на подсвечивание транспаранта автомат выдаст тогда, когда нажмут кнопки все трое судей или двое, один из которых – старший. Сконструировать автомат.
1-й шаг. Описание задачи, которую должен решать автомат принято называть словесной формой задания автомата. Автомат предстает при этом как некий “черный ящик”: еще неизвестно как будет устроен внутри, но уже ясно, что ему предстоит делать, известно как он связан с внешней средой. В данном случае будущий автомат имеет три входа – это линии, по которым поступают сигналы от судей А, В и С и один выход Х (сигнал для подсвечивания транспаранта “вес взят правильно”).

Рис. 2
3-й шаг. Теперь можно составить таблицу работы автомата.

Рис. 3

Рис.4

Рис. 5
IX. Разбор домашнего задания (на следующий урок):
Выучить новые понятия конспекту урока в тетради
№ 1. Постройте схему для логической функции F (a, b, c) = ( ¬ a & ¬ b) & (c v ¬ a) & c.
№ 2. Дана логическая схема:

Рис. 6
Составьте логическую функцию, которая ей соответствует. Найдите значения выходного сигнала.
+ Сформулировать алгоритм построения структурных формул и функциональных схем при решении задач о синтезе однотактных автоматов.
+ № 3. Три цеха – А, В и С – обеспечивает электроэнергией небольшая электростанция, на которой установлены два генератора – Х и Y. Если в энергии нуждается один из трех цехов, то достаточно включить генератор Y. Если же в энергии нуждаются два цеха одновременно – достаточно генератора Х. Снабжение всех трех цехов одновременно обеспечивается совместной работой генераторов X и Y. Необходимо построить такой автомат, который получая заявки от цехов А, В и С на снабжение энергией, может разумно перераспределять нагрузку между генераторами.
X. Самостоятельная работа: решение в тетрадях задачи № 1 и № 2. На решение отводится 7 минут.
Прежде чем решать задачу, подумай, что делать с ее решением!
Д.Пойа
№ 1. Постройте логическую схему выражения f = не (а или b) и (с или b).
Определите значение логического выражения, если а = истина, b = ложь, с = истина.
№ 2. Сконструировать автомат для подсчета голосов при тайном голосовании. Голосуют три человека. Автомат выдаст сигнал “избран”, если число голосов “за” не менее двух.
Дополнительное задание: № 3.

Рис. 7
Дополнительное задание: № 4 (см. Приложение 7 (“Дополнительное задание для самостоятельной работы”)).
XI. Подведение итогов урока:
– Выставление оценок, выборочный сбор тетрадей (“у менее активных учеников”; цель: выяснить, как и они, в том числе, усвоили материал урока.).
1. Оценить работу класса и назовите учащихся, отличившихся на уроке.
2. Выборочный сбор тетрадей (“у менее активных учеников”; цель: выяснить, как и они, в том числе, усвоили материал урока.).
– Нами были рассмотрены различные задачи, основанные на построении логических схем. Приемы для их решения различны. Мы, конечно, рассмотрели далеко не все возможные способы решения подобных задач. Возможно, вы найдете более простой и более интересный по сравнению с рассмотренными. Из этого можно сделать вывод, что, решая, какую-либо задачу не надо останавливаться на каком-то одном приеме, ведь вероятнее всего эту же задачу можно решить и другим методом, который будет и легче и проще для данной задачи. Я еще раз призываю вас “учиться думать красиво”.
– Работая в группах, вы выделили в каждой группе одного самого активного. Я согласна с вашей оценкой их работы и тоже оцениваю их работу сегодня, на «отлично». Но мне хотелось бы убедиться, что и все остальные поняли эту тему не хуже. Поэтому по окончании урока попрошу некоторых из вас сдать тетрадь с самостоятельной работой на проверку.
– Надеюсь, что все, что мы сегодня с вами делали на уроке, было и понятно, и интересно. По крайней мере, мне с вами работать было приятно. Спасибо всем за урок!
Видео:Решить систему логических уравнений. Метод декомпозицииСкачать

Логические схемы. Решение задач.
С помощью данного материала можно закрепить и проверить уровень понимания учащихся по теме Построение логических схем.
Просмотр содержимого документа
«Логические схемы. Решение задач.»
Составить логическую схему для следующего логического выражения найдите ответ:
Постройте логическую схему, соответствующую логическому выражению F = X & Y V ¬(Y V X) . Вычислить значения выражения для X=1 , Y=0 .
Постройте логическую схему по логическому выражению и найдите значение логического выражения
Постройте логическую схему по логическому выражению и найдите значение логического выражения
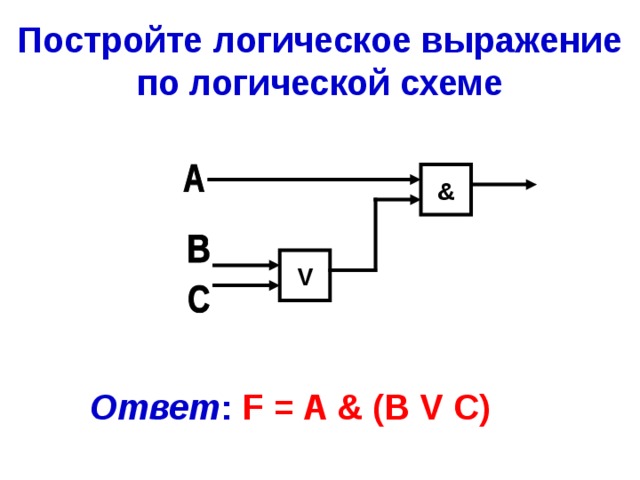
Постройте логическое выражение по логической схеме
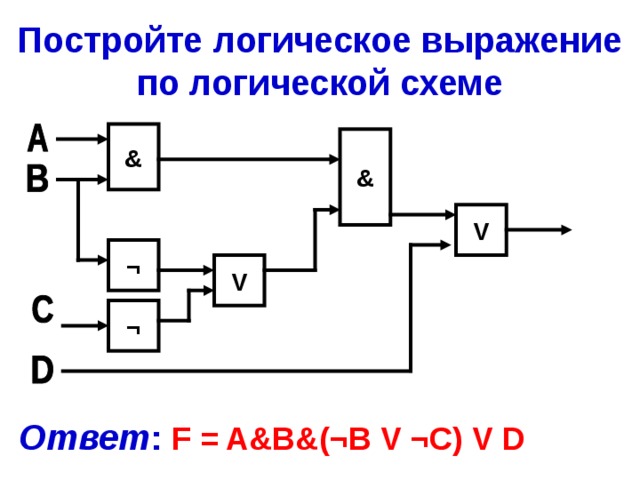
Постройте логическое выражение по логической схеме
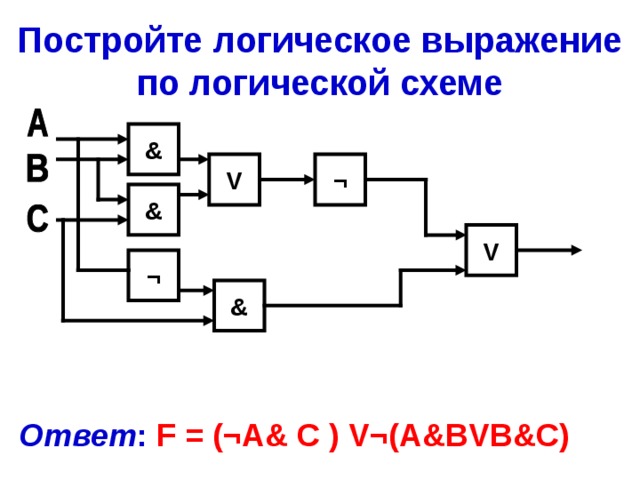
Постройте логическое выражение по логической схеме
Постройте логическое выражение по логической схеме
Составьте логические схемы к логическим выражениям:
🎬 Видео
Преобразование логических выражений / Упрощение выражений (практика) [Алгебра логики] #6Скачать
![Преобразование логических выражений / Упрощение выражений (практика) [Алгебра логики] #6](https://i.ytimg.com/vi/S2bMFkhdA9Y/0.jpg)
Шифраторы, дешифраторы. Назначение, принцип работы, типовые схемы.Скачать

[МИФ] Информатика ЕГЭ. № 2.2. Таблицы истинности логических выражений. Немонотонные функцииСкачать
![[МИФ] Информатика ЕГЭ. № 2.2. Таблицы истинности логических выражений. Немонотонные функции](https://i.ytimg.com/vi/BkTXlasgJu0/0.jpg)
Логическая функция F || 2 задача || ЕГЭ ИнформатикаСкачать

Информатика ЕГЭ. № 2.3.2. Таблицы истинности. Строки с пропущенными значениямиСкачать

Сколько решений имеет логическое уравнение: (A импликация В) ИЛИ (C импликация D). ЕГЭ(информатика)Скачать

ЛОГИЧЕСКИЕ ОПЕРАЦИИ - ЕГЭ информатика - 2 заданиеСкачать

Построение таблиц истинностиСкачать

Информатика 10 класс (Урок№11 - Алгебра логики. Таблицы истинности.)Скачать

Решение логических задач | Информатика 8 класс #15 | ИнфоурокСкачать