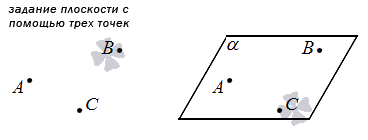Взаимное расположение прямых и плоскостей в пространстве уравнения прямой и плоскости

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Взаимное расположение прямой и плоскости в пространстве.
Признак параллельности прямой и плоскости

Все возможные случаи взаимного расположения прямой и плоскости в пространстве представлены в следующей таблице.

Прямая лежит на плоскости, если все точки прямой принадлежат плоскости.

Замечание . Для того, чтобы прямая лежала на плоскости, необходимо и достаточно, чтобы две любые точки этой прямой принадлежали этой плоскости.

Прямая пересекает плоскость, если прямая и плоскость имеют единственную общую точку.

Прямая параллельна плоскости, если прямая и плоскость не имеют общих точек. (они не пересекаются)

Фигура	Рисунок	Формулировка
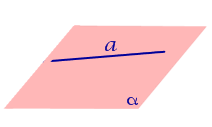
Прямая лежит на плоскости (принадлежит плоскости)
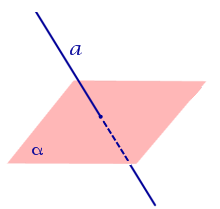
Прямая пересекает плоскость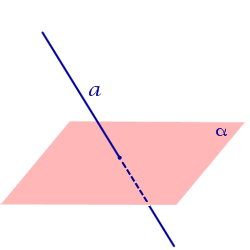
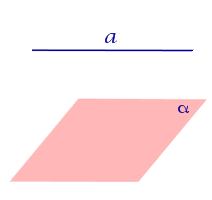
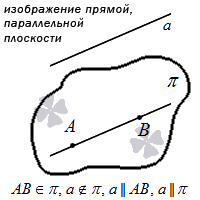
Прямая параллельна плоскости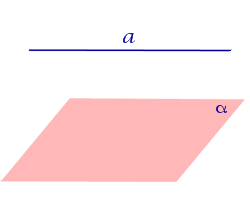

Прямая лежит на плоскости, если все точки прямой принадлежат плоскости.

Замечание . Для того, чтобы прямая лежала на плоскости, необходимо и достаточно, чтобы две любые точки этой прямой принадлежали этой плоскости.

Прямая пересекает плоскость, если прямая и плоскость имеют единственную общую точку.

Прямая параллельна плоскости, если прямая и плоскость не имеют общих точек. (они не пересекаются)

Утверждение 1 . Предположим, что прямая a и плоскость α параллельны, а плоскость β проходит через прямую a . Тогда возможны два случая:

Рис.1Рис.2

Рис.1

Рис.2

Доказательство . Рассмотрим случай 2 и предположим противное. Предположим, что прямые a и b пересекаются в некоторой точке P (рис.3) .

Но тогда точка P оказывается точкой пересечения прямой a и плоскости α , и мы получаем противоречие с тем, что прямая a и плоскость α параллельны. Полученное противоречие и завершает доказательство утверждения 1.

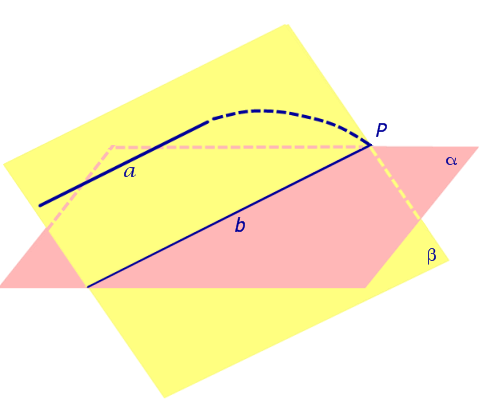
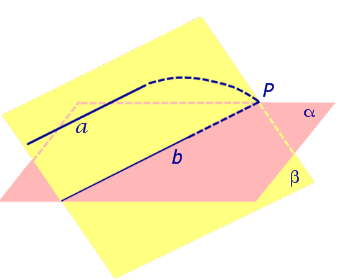
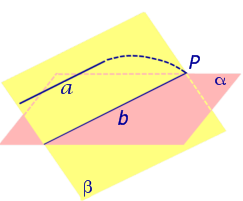
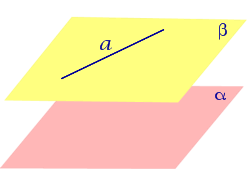
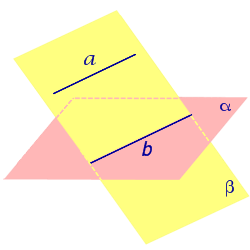
Утверждение 2 (признак параллельности прямой и плоскости) . Если прямая a , не лежащая в плоскости α , параллельна некоторой прямой b , лежащей в плоскости α , то прямая a и плоскость α параллельны.

Доказательство. Докажем признак параллельности прямой и плоскости «от противного». Предположим, что прямая a пересекает плоскость α в некоторой точке P . Проведем плоскость β через параллельные прямые a и b Проведем плоскость β через параллельные прямые a и b (рис. 4).

Точка P лежит на прямой a и принадлежит плоскости β. Но по предположению точка P принадлежит и плоскости α , следовательно точка P лежит на прямой b , по которой пересекаются плоскости α и β . Однако прямые a и b параллельны по условию и не могут иметь общих точек.

Полученное противоречие завершает доказательство признака параллельности прямой и плоскости.

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Плоскость в пространстве – необходимые сведения

Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.

Видео:22. Взаимное расположение прямой и плоскости в пространствеСкачать

Понятие плоскости и ее обозначения

Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.

В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.

Прямые и точки, размещенные в пространстве, мы будем обозначать аналогично размещенным на плоскости – с помощью строчных и прописных латинских букв ( B , A , d , q и др.) Если в условиях задачи у нас есть две точки, которые расположены на прямой, то можно выбрать такие обозначения, которые будут соответствовать друг другу, например, прямая D B и точки D и B .

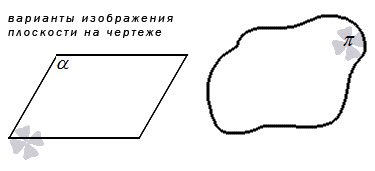
Чтобы обозначить плоскость на письме, традиционно используются маленькие греческие буквы, например, α , γ или π .

Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.

Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.

Видео:Геометрия. 10 класс. Взаимное расположение прямых и плоскостей в пространстве /03.11.2020/Скачать

Как могут располагаться плоскость и точка друг относительно друга

Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:

В любой плоскости есть точки.

Такой вариант расположения также называется прохождением плоскости через точку. Чтобы обозначить это на письме, используется символ ∈ . Так, если нам нужно записать в буквенном виде, что через точку A проходит некая плоскость π , то мы пишем: A ∈ π .

Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.

Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.

Зная это правило, можно ввести новое обозначение плоскости. Вместо маленькой греческой буквы мы можем использовать названия точек, лежащих в ней, например, плоскость А В С .

Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:

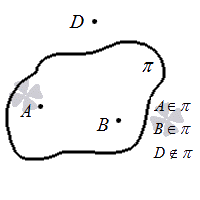
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.

Выше мы уже отмечали, что для обозначения плоскости в пространстве будет достаточно трех точек, а четвертая может находиться как в ней, так и вне ее. Если нужно обозначить отсутствие принадлежности точки к заданной плоскости на письме, то используется знак ∉ . Запись вида A ∉ π правильно читается как «точка A не принадлежит плоскости π »

Графически последнюю аксиому можно представить так:

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Варианты взаимного расположения прямой и плоскости

Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:

Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.

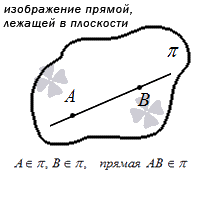
Чтобы записать принадлежность прямой некой плоскости, используем тот же символ, что и для точки. Если мы напишем « a ∈ π », то это будет означать, что у нас есть прямая a , которая расположена в плоскости π . Изобразим это на рисунке:

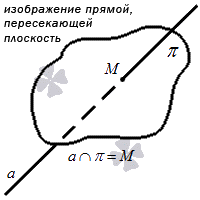
Второй вариант взаимного расположения – это когда прямая пересекает плоскость. В таком случае у них будет всего одна общая точка – точка пересечения. Для записи такого расположения в буквенном виде используем символ ∩ . Например, выражение a ∩ π = M читается как «прямая a пересекает плоскость π в некоторой точке M ». Если у нас есть точка пересечения, значит, у нас есть и угол, под которым прямая пересекает плоскость.

Графически этот вариант расположения выглядит так:

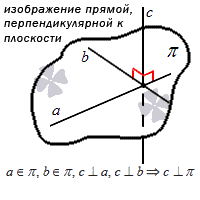
Если у нас есть две прямые, одна из которых лежит в плоскости, а другая ее пересекает, то они являются перпендикулярными друг другу. На письме это обозначается символом ⊥ . Особенности такой позиции мы рассмотрим в отдельной статье. На рисунке это расположение будет выглядеть следующим образом:

Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.

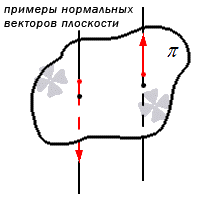
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.

Примеры нормальных векторов плоскости показаны на рисунке:

Третий случай взаимного расположения прямой и плоскости – это их параллельность. В таком случае ни одной общей точки у них нет. Для указания таких отношений на письме используется символ ∥ . Если у нас есть запись вида a ∥ π , то ее следует читать так: «прямая a является параллельной плоскости ∥ ». Подробнее этот случай мы разберем в статье про параллельные плоскости и прямые.

Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.

Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Варианты расположения двух плоскостей друг относительно друга

1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.

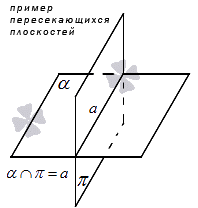
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:

Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.

На графике это будет выглядеть так:

В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.

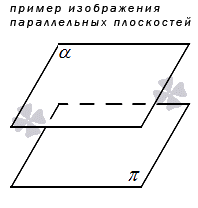
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.

Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.

Видео:15. Взаимное расположение прямых в пространствеСкачать

Как задать плоскость в пространстве

В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.

1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.

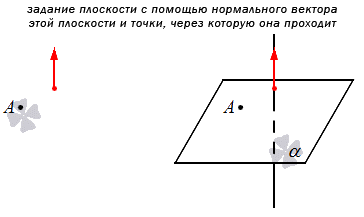
Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:

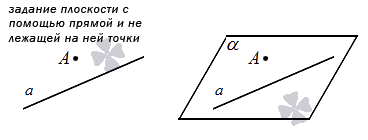
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:

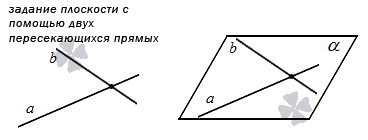
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:

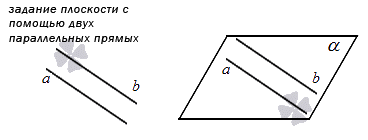
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.

На рисунке этот способ будет выглядеть так:

Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:

Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.

Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).

Вспомним одну теорему, изученную в рамках курса по геометрии:

Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.

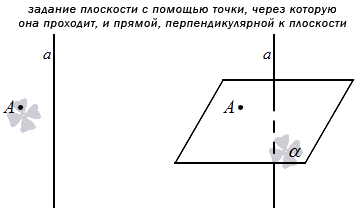
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.

Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.

Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.

Видео:Геометрия 10 класс (Урок№5 - Взаимное расположение прямых в пространстве.)Скачать

Урок «Взаимное расположение прямых и плоскостей в пространстве»

Разделы: Математика

Класс: 10

Учебная дисциплина: «Математика: алгебра и начала математического анализа, геометрия».

Тип занятия: урок изучения и первичного закрепления новых знаний.

Вид занятия: комбинированный урок (исследовательская работа, беседа).

Продолжительность: 90 минут.

Цели занятия: обеспечить оценку и проверку знаний; создать условия для развития у обучающихся умения формулировать проблемы, предлагать пути их решения, для формирования системы знаний, связанных с понятиями взаимного расположения прямых и плоскостей в пространстве, содействовать умению общаться между собой; формировать умения делать обобщения на основе полученных данных в результате исследования, исследовать решение простейших задач стереометрии по данной теме.

По окончанию занятия обучающийся имеет практический опыт:

Знает:

• случаи взаимного расположения прямых в пространстве;
• случаи взаимного расположения плоскостей в пространстве;
• случаи взаимного расположения прямых и плоскостей в пространстве.

Умеет:

• организовывать поиск, сбор и получение информации о взаимном расположении прямых и плоскостей в пространстве и ее применении при решении задач, находить связь стереометрии с окружающим миром, решать простейшие задачи стереометрии.

Владеет: умением анализировать, сравнивать, аргументировать свои ответы.

Дидактические задачи:

• обучающие: рассмотреть возможные случаи взаимного расположения прямых и плоскостей в пространстве; познакомить с его применением в жизни; формировать навык чтения чертежей, пространственных конфигураций к задачам.
• развивающие: развивать пространственное воображение учащихся при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание; вырабатывать самостоятельность в освоении новых знаний.
• воспитательные: воспитывать у учащихся ответственное отношение к учебному труду, формировать эмоциональную культуру и культуру общения, развивать чувство патриотизма, любви к природе.

Методическая цель:

• Использовать приемы, активизирующие внимание и память;
• Продемонстрировать возможность использования на уроке информационных технологий, организацию фронтальной и индивидуальной работы.

Методы обучения: Проблемно-поисковый, деятельностный, метод беседы, методы организации и осуществления учебно-познавательной деятельности, методы контроля и самоконтроля за эффективностью учебно-познавательной деятельности.

Формы организации познавательной деятельности: Фронтальная, работа в парах, индивидуальная работа.

Средства технологической поддержки учебной работы:

• ноутбук,
• проектор,
• презентация по теме «Взаимное расположение прямых и плоскостей в пространстве».
• экран,
• Рабочая тетрадь для записи конспекта
• Рабочая программа, календарно-тематический план, план занятия.

Межпредметные связи:

• Обеспечиваемые – информатика, черчение, ИЗО;
• Обеспечивающие – информатика, геометрия, реальная математика.

Структура и методический инструментарий учебного занятия

Этапы
занятия

Методические приемы и методы обучения

Деятельность преподавателя

Деятельность студентов

1. Организационный момент.
Задача:
Обеспечить благоприятную внешнюю обстановку для работы на занятии, благоприятный микроклимат, психологическую подготовку студентов к восприятию материала.

Методы формирования внимания долга ответственности, стремление познать новое.

Создание в аудитории рабочей обстановки, проверка отсутствующих.
Преподаватель сообщает план работы урока, мотивирует студентов к деятельности.

Обучающиеся настраиваются на урок, бегло повторяют домашнее задание, быстрое включение в деловой ритм, установка внимания всей группы.

2. Проверка изученного ранее

Метод передачи информации с помощью практической деятельности

Предлагает ответить на вопросы самостоятельной работы

Слушают преподавателя;
выполняют работу;

3. Изучение и первичное закрепление новых знаний.
Задача:
Изучить различные виды взаимного расположения прямых и плоскостей в пространстве, сформировать основные понятия по теме, применить полученные знания для решения задач.

Метод словесной передачи информации
и слухового восприятия информации.
Метод наглядности передачи информации и зрительного восприятия информации. Иллюстрация (слайды презентации).

Определяет цели предстоящей работы; знакомит студентов с порядком выполнения работы;
знакомит студентов с основными вопросами темы, предлагает задачи для закрепления, комментирует выполняемую работу.

Слушают преподавателя;
выполняют работу; комментируют выполненную работу, записывают в сопроводительный лист определения, решение задач.

4. Закрепление нового материала
Задача:
Установление правильности и осознанности усвоения нового учебного материала, выявление пробелов и неверных представлений и их коррекция.

Метод передачи информации с помощью практической деятельности, метод консультирования и взаимопомощи.

Предлагает решение задач с последующей самопроверкой.

Самостоятельное выполнение заданий, требующих применения новых знаний: решение задач.

5. Подведение итогов занятия.
Задача:
Дать анализ и оценку успешности достижения цели и наметить перспективу последующей работы.

Метод самооценки и оценки знаний.

Кратко напоминает цель урока. Предлагает подвести итоги, выставить оценки за урок. Объявляет критерии итоговой оценки.

Высказывают свое мнение о достижении поставленной цели.

6. Рефлексия.
Задача:
Мобилизация студентов на рефлексию (мотивация способов деятельности, общения). Усвоение принципов саморегуляции и сотрудничества.

Установление логических связей и развитие аналитико-рефлексивных способностей.

Предлагает ответить на вопросы:
Достиг ли ты своих целей?
Оцени степень усвоения.
Продолжи одно из предложений:
“Мне понятно…
“Я запомнил…
“Мне на уроке…
“Я думаю…

Открытость студентов в осмыслении своих действий и самооценки. Прогнозирование способов саморегуляции и сотрудничества.

7. Информации о домашнем задании, инструктаж по его выполнению.
Задача:
Сообщить студентам о домашнем задании, разъяснить методику, его выполнения и критерии оценки.

Метод контроля и самоконтроля, метод словесной передачи информации и ее слухового восприятия.

Ставит перед обучающимися проблему, разъясняет пути ее решения.

Слушают преподавателя осмысливают, записывают условия выполнения задания.

Ход урока

1. Организационный момент. Постановка цели и задач урока. (3 мин)

Преподаватель проверяет готовность к уроку.

Я рада приветствовать всех Вас сегодня на занятии. Все мы пришли с разным настроением, но я надеюсь, что тема, которую мы сегодня изучим, будет для вас настолько интересна, что в конце нашего занятия у нас у всех будут только положительные эмоции.

2. Проверка изученного ранее

Вам предлагается небольшая самостоятельная работа. (10 мин)

1) Стереометрия – это …

2) Основные (простейшие) фигуры в пространстве — …

3) Изобразите и обозначьте: точку, прямую, плоскость

4) Примеры геометрических тел:…

5) Сформулируйте АКСИОМЫ стереометрии

6) Решите задачу.

Пользуясь данным рисунком, запишите:

а) четыре точки, лежащие в плоскости SAB, в плоскости АВС;

б) плоскость, в которой лежит прямая MN, прямая КМ.

3. Изучение и первичное усвоение новых знаний

Введение новых понятий (40 мин)

В практической деятельности нам часто приходится иметь дело с простейшими понятиями стереометрии- точками, прямыми и плоскостями. Умение анализировать, представлять их взаимное расположение, делать правильные выводы является важным качеством каждого мыслящего человека. Без понятия взаимного расположения прямых и плоскостей в пространстве невозможно решить ни одной стереометрической задачи. Поэтому отнеситесь к данной теме очень серьезно, внимательно слушайте, не отвлекайтесь.

Демонстрация презентации. Студенты заполняют конспект в рабочей тетради.

1. Взаимное расположение прямых в пространстве

1. Параллельные прямые

2. Пересекающиеся прямые

3. Скрещивающиеся прямые

1. Параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются
2. Две прямые называются пересекающимися, если они лежат в одной плоскости и имеют общую точку.
3. Прямые называются скрещивающимися, если они не лежат в одной плоскости.

Признак скрещивающихся прямых: Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то такие прямые являются скрещивающимися.

Составьте схему взаимного расположения двух прямых в пространстве:

№ 1.

а.) Запишите две пары пересекающихся прямых;________________________
б) Запишите две пары параллельных прямых;___________________________
в) Запишите две пары скрещивающихся прямых.________________________

2. Взаимное расположение плоскостей в пространстве

1) Параллельные плоскости

Плоскости, не имеющие общих точек, называются параллельными

2) Пересекающиеся плоскости

Плоскости называются пересекающимися, если они имеют общие точки

№2

а) прямую, по которой пересекаются плоскости B₁CD и AA₁D₁; плоскости ADC₁ и A₁B₁B;

№3.

Пользуясь данным рисунком, запишите:

а) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB.

б) прямую, по которой пересекаются плоскости DEF и SBC; плоскости FDE и SAC;

в) две плоскости, которые пересекает прямая SB; прямая AC.

Составьте схему взаимного расположения двух плоскостей в пространстве

3. Взаимное расположение прямых и плоскостей в пространстве

1) Прямая параллельна плоскости

Прямая и плоскость называются параллельными, если они не пересекаются и не имеют общих точек.

2) Прямая пересекает плоскость

Плоскость и прямая называются пересекающимися, если они имеют общую точку пересечения.

3) Прямая лежит в плоскости

Прямая лежит в плоскости, если все точки прямой принадлежат данной плоскости.

Составьте схему взаимного расположения прямой и плоскости в пространстве.

4. Закрепление нового материала. (20 мин)

А сейчас математический диктант.

1. Определите взаимное расположение прямых. Слайды 18-21.

2. Определите взаимное расположение прямых и плоскостей. Слайды 23-26.

3. Определите взаимное расположение плоскостей. Слайды 28-30.

А сейчас проверьте ваше решение, если у вас правильно, поставьте +, если неверно, то поставьте – и исправьте неверное решение.
Поставьте себе оценку.

А сейчас решаем задачи на закрепление.

№4. Через конец A отрезка AB проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В₁ и С₁. Найдите длину отрезка ВВ₁ если:

1) СС₁ = 15 см, АС : ВС = 2 : 3;

2) СС₁ = 8,1 см, АВ : АС =11 : 9;

3) АВ = 6 см, АС : СС₁ =2 : 5.

№5. Прямые а и b не лежат в одной плоскости. Можно ли провести прямую с, параллельную прямым а и b?

5. Подведение итогов занятия. (5 мин)

Подведем итоги нашего занятия. Обсуждение и выставление оценок за урок: за урок будут выставлены две оценки- одна за самостоятельную работу в начале урока, вторая за диктант и конспект занятия.

6. Рефлексия. (3 мин)

Посмотрите на тему нашего занятия. Раскрыта ли тема занятия?

Оцени степень усвоения: ________________________

Продолжи одно из предложений:

7. Домашнее задание. (2 мин)

Решить задачу (дифференцированные задачи)

Задача на «3» Выучить теоретический материал занятия. Разгадайте кроссворд.

1. Раздел геометрии, в котором изучаются свойства фигур в пространстве.

2. Математическое утверждение, не требующее доказательства.

3. Одна из простейших фигур и планиметрии и стереометрии.

4. Раздел геометрии, в котором изучаются свойства фигур на плоскости.

5. Защитное приспособление воина в виде круга, овала, прямоугольника.

6. Теорема, в которой по заданному свойству нужно определить предмет.

7. Направленный отрезок.

8. Планиметрия — плоскость, стереометрия — :

9. Женская одежда в форме трапеции.

10. Одна точка, принадлежащая обеим прямым.

11. Какую форму имеют гробницы фараонов в Египте?

12. Какую форму имеет кирпич?

13. Одна из основных фигур в стереометрии.

14. Она может быть прямой, кривой, ломаной.

Задача на «4» Выучить теоретический материал занятия.

1. Постройте 4 точки, которые лежат в плоскости α. и 4 точки, которые не лежат в плоскости α.
2. несколько прямых, которые лежат в плоскости α.
3. несколько прямых, которые не лежат в плоскости α.
4. несколько прямых, которые пересекают прямую ВС
5. несколько прямых, которые не пересекают прямую ВС.

Задача на «5» Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А₁, В₁ и М₁. Найдите длину отрезка MM₁, если отрезок АВ не пересекает плоскость и если AA₁ = 5 м, ВВ₁ = 7 м.

Литература

1. Атанасян. Геометрия 10 -11 кл.: учебник – М., 2014.

2. Башмаков М.И. Математика: учебник для студ. учреждений сред. проф. образования / М.И.Башмаков. – 9-е изд., стер. – М. Издательский центр «Академия», 2014. – 256 с.

3. Башмаков М.И. Математика. Задачник : учеб. пособие для студ. учреждений сред. проф. образования / М.И.Башмаков. – 5-е изд., стер. – М. : Издательский центр «Академия», 2014. – 416 с.

4. Математика. 10–11 классы: элективный курс «В мире закономерных случайностей»/ авт.-сост. В.Н.Студенецкая и др.: Волгоград: Учитель, 2007. -126с.

📸 Видео

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Геометрия. 10 класс. Взаимное расположение прямой и плоскости /06.10.2020/Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

11. Прямая в пространстве и ее уравненияСкачать

Взаимное расположение прямых на плоскости. 7 класс.Скачать

Лекция 5. Взаимное расположение двух прямых, прямой и плоскости, двух плоскостейСкачать

Стереометрия 10 класс. Часть 2 | Математика | TutorOnlineСкачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать