Вывод уравнения моментов из законов ньютона

Лекция №6.

Закон сохранения импульса.

Закон сохранения энергии.

3. Пример расчёта динамики бронеавтомобиля.

Закон сохранения импульса.

Выпишем второй закон Ньютона.

, (1)

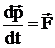
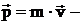
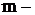
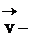
где импульс тела, масса объекта, скорость его движения,

действующая сила.

Физический смысл импульса становится очевидным, если уравнение (1) проинтегрировать на конечном интервале времени :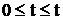

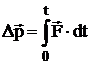
. (2)

Из выражения (2) следует, что изменение импульса служит мерой величины силы, действующей на тело в течение конечного промежутка времени.

Далее, рассмотрим ситуацию в отсутствие внешних сил, то есть, .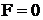

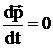
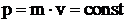
Из уравнения (1) получаем, что , т.е. величина импульса, , остается постоянной во все время движения. Полученный результат представ­ляет собой закон сохранения импульса.

Формулировка.

Для замкнутой системы (без внешних воздействий!) её интегральный импульс есть

Величина постоянная.

, где число объектов в системе (3).

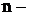
Закон сохранения энергии.

Механическая работа, совершаемая некоторой силой на заданном участке пути – это физическая величина, определяемая как скалярное произведение вектора силы на длину соответствующего участка.

Энергия – это физическая величина, определяющая способность объекта совершать работу (вычисляется как РАБОТА!)

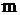
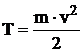
Кинетической энергией объекта массы , движущегося со скоростью , называется величина, равная .

Пусть объект находится в поле сил, действие которых зависит только от его положения в пространстве. Пусть такое поле можно описать с помощью некоторой скалярной функции 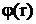, зависящей, только от координат.

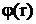
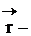
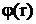
Поле сил называется потенциальным полем, если это поле описывается скалярной функцией , зависящей только от координат ( радиус-вектор). Функция называется потенциалом поля.

Сила действия поля связана с потенциалом в каждой точке соотношением:

, (1)

где постоянная – 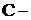определяется свойствами объекта в поле сил.

Величина называется потенциальной энергией объекта в потенциальном поле .

В классической механике утверждается частный случай всеобщего Закона сохранения энергии — Закон сохранения механической энергии!

Формулировка.

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.

Проще говоря, при отсутствии внешних или диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть никуда.

Классическим примером этого утверждения являются пружинный (рис. а) или математический (рис. б) маятники с пренебрежимо малым затуханием.

В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно.

В случае математического маятника аналогично ведёт себя потенциальная энергия груза в поле силы тяжести.

Вывод из уравнений Ньютона.

Закон сохранения механической энергии может быть выведен из второго закона Ньютона, если учесть, что в консервативной системе все силы, действующие на тело, потенциальны.

Тогда, с использованием соотношения (1), записываем, что

, (2)

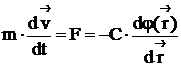
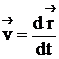
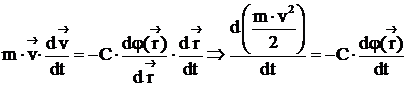
Домножив скалярно, обе части данного уравнения на скорость объекта, и приняв во внимание, что , можно получить, что

,

И далее, путём элементарных операций это выражение может быть приведено к следующему виду:

Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени сохраняется, то есть, сумма кинетической и потенциальной энергий есть постоянная величина ( ).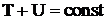

Подчеркнём, что эта сумма и называется полной механической энергией материального объекта. Первый член в сумме отвечает кинетической энергии, второй — потенциальной.

Этот вывод может быть легко обобщён на любую механическую систему.

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Уравнение моментов: моменты силы, импульса и инерции

Если линейное перемещение тел описывают в классической механике с помощью законов Ньютона, то характеристики движения механических систем по круговым траекториям вычисляют с помощью специального выражения, которое называется уравнением моментов. О каких моментах идет речь и в чем заключается смысл этого уравнения? Эти и другие вопросы раскрываются в статье.

Видео:Три Закона Ньютона. Простое ОбъяснениеСкачать

Момент силы

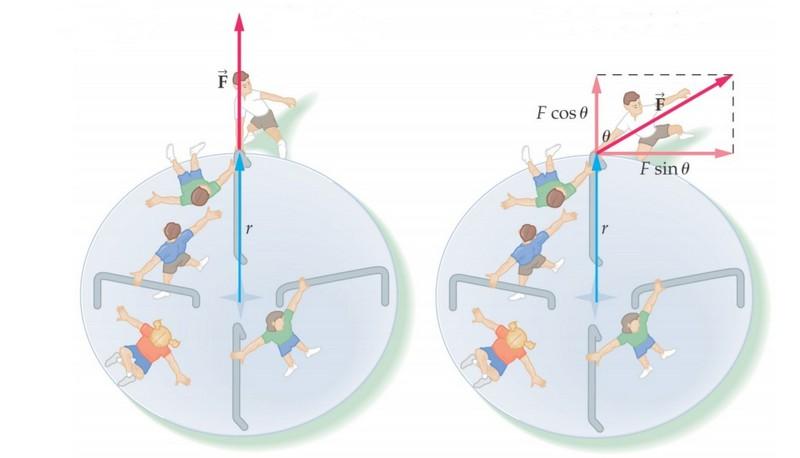
Всем хорошо известна ньютоновская сила, которая, действуя на тело, приводит к сообщению ему ускорения. Когда же такая сила прилагается к объекту, который закреплен на некоторой оси вращения, то эту характеристику принято называть моментом силы. Уравнение момента силы может быть записано в следующем виде:

Рисунок, поясняющий это выражение, приведен ниже.

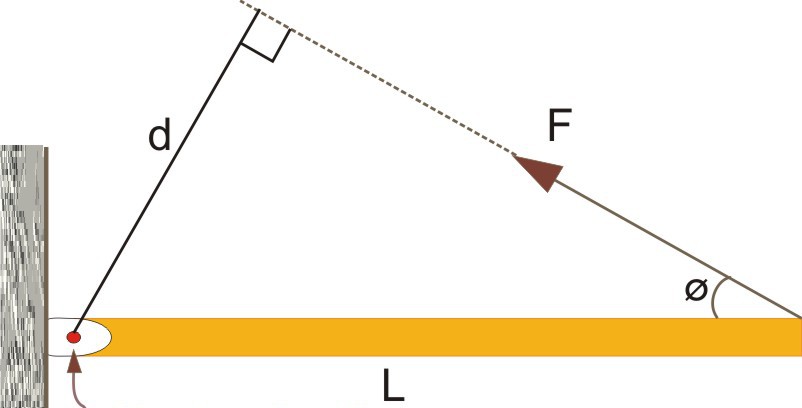
Здесь видно, что сила F¯ направлена к вектору L¯ под углом Φ. Сам же вектор L¯ полагается направленным от оси вращения (указана стрелкой) к точке приложения F¯.

Приведенная выше формула представляет собой произведение двух векторов, поэтому величина M¯ также является направленной. Куда будет повернут момент силы M¯? Это можно определить по правилу правой руки (четыре пальца направлены вдоль траектории от конца вектора L¯ к концу F¯, а отставленный палец большой показывает направление M¯).

На рисунке выше выражение для момента силы в скалярном виде примет форму:

Если внимательно всмотреться в рисунок, то можно увидеть, что L*sin(Φ) = d, тогда имеем формулу:

Величина d является важной характеристикой при вычислении момента силы, поскольку она отражает эффективность приложенной F к системе. Эту величину принято называть рычагом силы.

Физический смысл M заключается в способности силы совершить вращение системы. Эту способность может ощутить на себе каждый, если будет открывать дверь за ручку, толкая ее около петель, или же попробует открутить гайку коротким и длинным ключом.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Равновесие системы

Понятие о моменте силы оказывается очень полезным, когда рассматривают равновесие системы, на которую действуют несколько сил, и которая имеет ось или точку вращения. В таких случаях применяют формулу:

То есть система будет находиться в равновесии, если сумма всех моментов сил, приложенных к ней, нулевая. Заметим, что в этой формуле присутствует знак вектора над моментом, то есть при решении следует не забывать учитывать знак этой величины. Общепринятым правилом считается, что действующая сила, которая вращает систему против часовой стрелки, создает положительный M_i¯.

Ярким примером задач рассматриваемого типа являются проблемы с равновесием рычагов Архимеда.

Видео:Семинар №6 "Момент инерции. Уравнения моментов" (Чивилев В.И.)Скачать

Момент импульса

Это еще одна важная характеристика движения по окружности. В физике ее описывают произведением количества движения на рычаг. Уравнение момента импульса имеет такой вид:

Здесь p¯ — вектор импульса, r¯ — вектор, соединяющий вращающуюся материальную точку с осью.

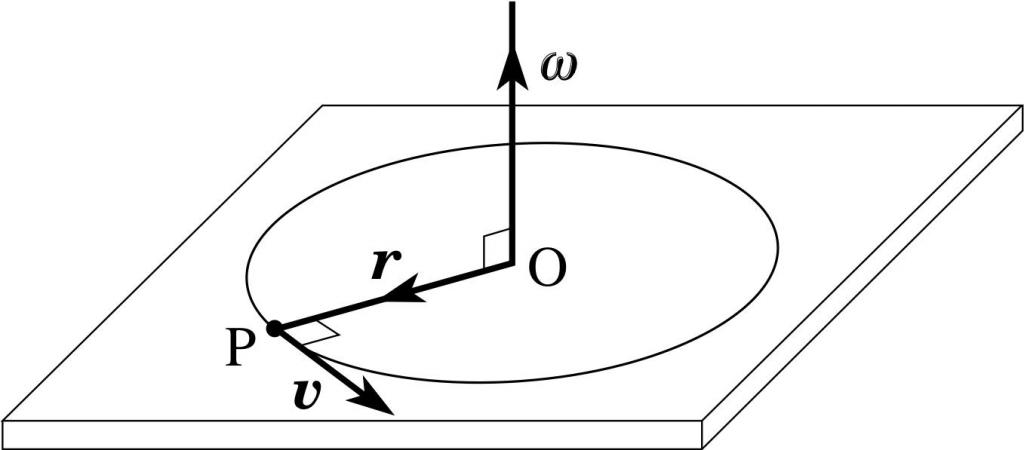
Поясняющий это выражение рисунок приведен ниже.

Здесь ω — угловая скорость, которая дальше появится в уравнении моментов. Заметим, что направление вектора T¯ находится по тому же правилу, что и M¯. На рисунке выше T¯ по направлению будет совпадать с вектором угловой скорости ω¯.

Физический смысл величины T¯ является таким же, как и характеристики p¯ в случае линейного движения, то есть момент импульса описывает количество вращательного движения (запасенную кинетическую энергию).

Видео:Алгоритм решения задач на второй закон Ньютона часть 1| Физика TutorOnlineСкачать

Момент инерции

Третья важная характеристика, без которой невозможно составить уравнение движения вращающегося объекта, — это момент инерции. Появляется он в физике в результате математических преобразований формулы для момента импульса материальной точки. Покажем, как это делается.

Представим величину T¯ в следующем виде:

T¯ = r¯*m*v¯, где p¯ = m*v¯

Пользуясь связью между угловой и линейной скоростями, можно переписать это выражение следующим образом:

T¯ = r¯*m*r¯*ω¯, где v¯ = r¯*ω¯

Последнее выражение запишем в виде:

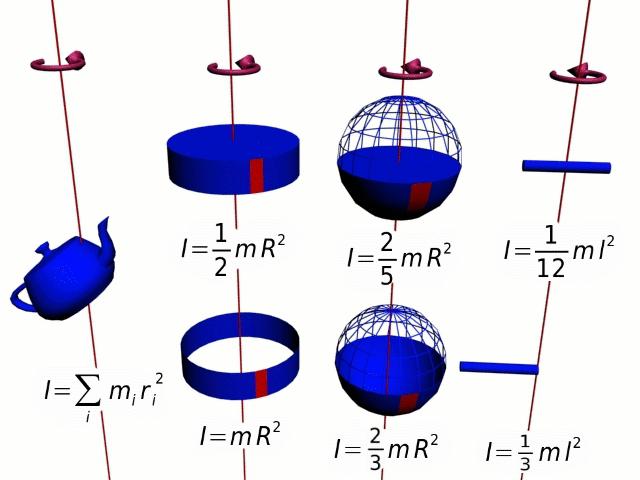
Величина r 2 *m — это момент инерции I для точки массой m, которая совершает круговое движение вокруг оси на расстоянии от нее r. Этот частный случай позволяет ввести общее уравнение момента инерции для тела произвольной формы:

I — это аддитивная величина, смысл которой заключается в инерционности вращающейся системы. Чем больше I, тем труднее раскрутить тело, и необходимо приложить значительные усилия, чтобы его остановить.

Видео:1.4. Законы Ньютона как уравнение движения | Динамика | Александр Чирцов | ЛекториумСкачать

Уравнение моментов

Мы рассмотрели три величины, название которых начинается со слова «момент». Это сделано было намеренно, поскольку все они связаны в одно выражение, получившее название уравнения 3 моментов. Выведем его.

Рассмотрим выражение для момента импульса T¯:

Найдем, как изменяется величина T¯ во времени, имеем:

Учитывая, что производная угловой скорости равна таковой для скорости линейной, деленной на r, а также раскрывая величину I, приходим к выражению:

dT¯/dt = m*r 2 *1/r*dv¯/dt = r*m*a¯, где a¯ = dv¯/dt — линейное ускорение.

Заметим, что произведение массы на ускорение — это не что иное, как действующая внешняя сила F¯. В итоге получаем:

Мы пришли к интересному выводу: изменение момента импульса равно моменту действующей внешней силы. Это выражение принято записывать в несколько иной форме:

M¯ = I*α¯, где α¯ = dω¯/dt — угловое ускорение.

Это равенство называется уравнением моментов. Оно позволяет рассчитать любую характеристику вращающегося тела, зная параметры системы и величину внешнего воздействия на нее.

Видео:Лекция №5 "Уравнение моментов" (Булыгин В.С.)Скачать

Закон сохранения T¯

Полученный в предыдущем пункте вывод свидетельствует о том, что если внешний момент сил будет равен нулю, то момент импульса меняться не будет. В таком случае запишем выражение:

Эта формула носит название закона сохранения величины T¯. То есть любые изменения внутри системы суммарный момент импульса не меняют.

Этот факт используется фигуристами и балеринами во время их выступлений. Также его применяют, если необходимо выполнить поворот вокруг своей оси искусственного спутника, движущегося в космосе.

Видео:Урок 94. Вычисление моментов инерции телСкачать

Вывод второго закона Ньютона для вращательного движения + примеры решения задач

Второй закон Ньютона для вращательного движения – главное тождество динамики, помогающее решить основную задачу механики для вращающегося тела: указать угол поворота тела в любой промежуток времени.

Задача механики поступательного движения считается решенной если в любое мгновение легко указать положение материальной точки относительно других тел, при условии, заданной системы отсчета.

Кроме поступательного существует вращательное движение – это такой вид движения при котором каждая точка движется по окружности, центры окружности лежат на одной прямой (оси вращения).

Характеристики вращательного движения:

• Всякая точка абсолютно твердого тела перемещается по дуге круга;
• «Ядра» окружностей расположены вдоль одной линии – ось вращения
• Разные точки передвигаются по разным траекториям;
• Зависимости перемещения по времени представляют отличные значения, изменяющиеся по направлению;
• Углы поворота точек – одинаковы.

Видео:Урок 76. Задачи на правило моментовСкачать

Аналоги характеристик поступательного и вращательного движения

Параметры вращательного перемещения необходимо рассматривать, проводя сравнение с характеристиками поступательного.

Последовательность нахождения координат тела в любой момент времени для поступательного перемещения:

1. зная силу F находим ускорение a;
2. из ускорения находи координаты x,y,z.

Пойдем от обратного для вращательного движения:

Найти нам необходимо угла поворота – φ в любой момент времени, для этого используем угловое ускорение ε, а вот аналог силы F мы пока не знаем.

Опишем кинематику вращательного движения.

• Аналог линейной скорости во вращательном движении это угловая скорость ω — выражается отношением:

— угол поворота

— незначительный отрезок времени

• Вспомним формулу линейной скорости υ точки находящейся на вращающемся теле, для этого умножим угловую скорость ω и r — расстояние от оси до искомой точки.

Виды вращательного движения:

Поворот предмета за равные промежутки времени на одинаковые углы говорит о равномерности перемещения. Угловое ускорение отсутствует.

Уравнение движения выглядит:

— угол поворота в любой момент времени,

— начальный угол поворота

Угловая скорость постоянна, но линейная скорость постоянно изменяет направление, а это означает, что существует центростремительное ускорение, направленное по радиусу к центру окружности.

1. Неравномерное вращение

При неравномерном перемещении постоянное угловое ускорение принимает вид:

При низменном , закон изменения угловой скорости получается:

Подставляя полученные данные в формулу движения при равномерном вращении получим:

Вспомним как рассчитать угол поворота тела тремя разными способами:

Второй способ (через среднюю скорость).

Сравнение формул вращательного и поступательного перемещения наглядно представлено таблично.

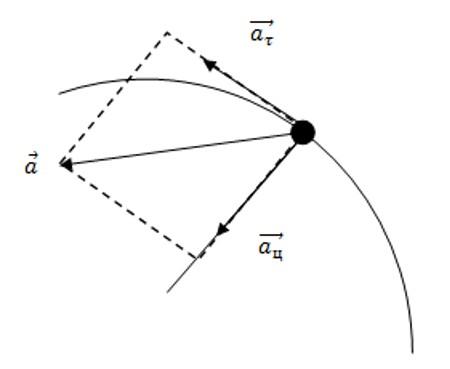
При нахождении точки на теле, неравномерно вращающемся на окружности, ускорение приобретает вид суммы:

— центростремительного и тангенциального

— тангенциального .

Сумма ускорений равна:

Тангенциальное ускорение вычисляется следующим образом

Используя связь υ и ω, получается:

Нужно сформулировать ключевые тождества, включая 2 закон сэра Ньютона для вращательного механического движения, сопутствующие обозначения, необходимые в ходе решения задач.

Видео:Физика . Законы Ньютона. ​Решение задач.Скачать

Вывод второго закона Ньютона для вращательного движения

Пусть тело, характеристиками которого можно пренебречь закреплено на невесомом стержне, 0 – ось вращения, длиной эквивалентной отрезку r.

На материальную точку оказывает воздействие силы , – реакция стержня.

— сила реакции нити;

— сила приводящая тело в движение

По II закону английского физика Исаака Ньютона второй закон динамики в векторной форме выглядит:

Выбор системы координат: Y – направляется по радиусу, Х – перпендикулярно.

Переписывая главное правило динамики в проекциях на эти оси:

Для этого на рисунке отобразим угол и выразим через него все проекции.

OX: ,

OY: ,

Из рисунка видно, что — тангенциальное ускорение, и – модуль центростремительного ускорения

Вспомним, что тангенциальное ускорение равно:

Перепишем уравнение проекции на ось x с учетом этого знания:

Вычислим угловое ускорение из полученной формулы:

Умножая на дробь на :

Далее надо визуально отобразить на рисунке rsinα.

Как видно из полученного рисунка перпендикуляр d – плечо силы F.

Сравнивая с выражением:

I=mr 2 – мера инертности тела, момент инерции.

Выходит: 2 закон Ньютона представлен для вращательного движения:

Словесная формулировка основного тождества динамики вращательного перемещения:

Алгебраическая сумма моментов сил, действующих на тело тождественно произведению момента инерции тела на его угловое ускорение.

Видео:Физика - первый и второй законы НьютонаСкачать

Практическое применение второго закона Ньютона для вращательного движения

Перемещение путем вращения часто находит практическое применение. Яркие примеры:

• Колеса транспортных средств;
• Шестеренки;
• Роторы электродвигателей.

Простые «мозголомки» из школьного курса физики

Задание 1. Велосипедное колесо

Определить меру инертности у велоколеса диаметром 67 см с массой 1,3 кг? Возможно, не учитывать массу ступицы?

Колесо целесообразно разбить на N мельчайших фрагментов размером Δl с массой Δm.

Мера инертности вычисляется из выражения:

кг х м 2

Задача 2. Взаимодействие кинематики и динамики

Материальная точка перемещается по окружности, ее радиальное ускорение изменяется пропорционально четвертой степени времени. Найти n из отношения .

Записывается второй закон Ньютона для вращательного движения:

Выражая угловую скорость:

Учитывая, неизменность расстояния до центра окружности, :

Упражнение 3. Графическое представление

Одно тело вращается по зависимости 1, потом действие момента сил изменяется согласно графику 2. Нужно сравнить угловые скорости в точках A и B.

Основной закон динамики перемещения путем вращения:

Поскольку тело одно, 1/I неизменно.

Геометрический смысл интеграла – площадь криволинейных трапеций.

Случай 1:

График 2:

Результат:

Получается:

Задание 4. Шары

Два точечных шарика, обладающие равными массами скреплены тонкой невесомой спицей l. Записать выражение момента инерции системы, относительно оси, перпендикулярно соотносящейся со спицей и центром масс.

Центр оси расположен между шарами:

Мера инертности системы:

Упражнение 5. Гири

Грузы массами 2 и 1 килограмм связаны ниткой, перекинутой через блок, весящий 1 килограмм. Вычислить ускорение перемещения гирь? Рассчитать натяжение нитей?

Векторный вид поступательного передвижения:

Перемещение диска – вращение:

Первые 2 равенства надо спроектировать на Х, последнее – Y. Записать уравнение кинематической связи. Получается система:

Подставляя 4 тождество в 3:

Вычитая (2) из (1), переписывается (5):

Численное значение из выражения (6) подставляется в (1) и (2):

Практическое применение в жизни

Автомобиль

Ускорится автомобиль, если установить шины большего диаметра?

Нет. Чем больше диаметр шин, тем выше линейное ускорение. Каждый автомобиль обладает максимальным угловым ускорением, соответствующее его мощности. Мощность машины ограничена, увеличение диаметра шин приведет к снижению углового ускорения, линейное не изменится.

«Что-то странная какая-то утка, на курицу похожа…»

Домашние птицы: селезень и курица имеют одинаковую длину шага. Почему курица бегает ровно, а селезень перемещается переваливаясь?

Расстановка лап селезня шире, центр тяжести расположен дальше от опоры, поэтому при ходьбе селезень вынужден делать поворот на больший угол. Момент силы тяжести от опоры увеличивается, соответственно становится больше величины угловых ускорения и скорости.

Гонки

Европейские гонки проходят по улицам города, поэтому гонщики не снижая большой скорости совершают резкие повороты. Двигатель гоночных машин расположен посередине авто. Содержание преимущества?

Двигатель посередине авто, обладает меньшей мерой инертности относительно центра масс, поэтому поворот осуществляется при меньшем моменте сил.

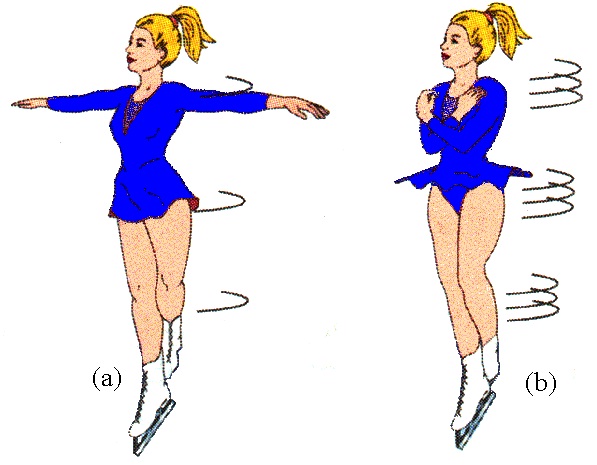
Фигурное катание

Зачем фигурист прижимает руки к телу?

Фигурист, вращаясь вокруг вертикальной оси, прижимает руки к корпусу. Момент инерции уменьшается, момент импульса остается неизменным, угловая скорость увеличивается.

Невесомость

Космонавт находится в невесомости. Как ему совершить поворот на 180˚ вокруг продольной оси?

Распутывание Гордиева узла:

Для поворота космонавт поднимает руку над головой, провоцируя поступательные движения в направлении, противоположенному повороту.

О кошках

Эмиль Кроткий утверждал: «Кошка мечтала о крыльях: ей хотелось попробовать летучих мышей». Люди не раз пытались подкидывать животное вверх ногами, при этом приземление всегда осуществляется на лапы. Момент внешних сил равен нулю, момент импульса сохраняется. Как кошке удается переворачиваться?

Момент импульса кошки, находящейся в свободном падении остается постоянным, моменты внешних сил отсутствуют. Вытягивая или прижимая к телу лапы, кошка изменяет меру инертности передней части тела относительно центральной оси от момента инерции задней части тела. Попеременно подтягивая передние или задние лапы, животное совершает поворот, ускоряющийся вращением хвоста.

Освоение 2 закона Исаака Ньютона с учетом кинематических и динамических характеристик для вращательного механического движения на практических примерах – легкое задание: надо запастись терпением, желанием приобретать знания. Изучать физику лучше вооружившись высказыванием Морихэй Уэсибы: «Двигайся, как луч света, летай, как молния, бей, как гром, вращайся вокруг устойчивого центра!»

🌟 Видео

Уравнение моментов, закон сохранения момента импульса и секториальная скоростьСкачать

Условия равновесия. Уравнения моментовСкачать

Урок 80 (осн). Момент силы. Правило моментовСкачать

Первый, второй, третий закон Ньютона. 10 класс.Скачать

Решение задач по теме Законы НьютонаСкачать

Применение II закона Ньютона. Разбор на примерахСкачать

Урок 55. Задачи на законы НьютонаСкачать

Урок 109. Момент импульса. Закон сохранения момента импульсаСкачать