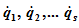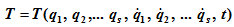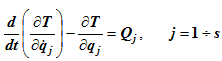Вывод уравнений лагранжа второго рода из принципа даламбера лагранжа (5 видео)

Вывод уравнений лагранжа второго рода из принципа даламбера лагранжа

Вывод уравнений Лагранжа 2-го рода.

Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения движения несвободной механической системы, составленные в обобщенных координатах. Рассмотрим движение системы, состоящей из N материальных точек, относительно ииерциальной системы отсчета. Наложенные на систему связи — голономные, удерживающие, идеальные. Если некоторые связи не идеальные, то соответствующие им реакции следует добавить к действующим на систему активным силам.

Видео:Вывод уравнения Лагранжа 2-го родаСкачать

ОБОБЩЕННЫЕ КООРДИНАТЫ, СКОРОСТИ И СИЛЫ. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА

Определение обобщенных координат дано в предыдущей главе. По существу, не употребляя этого термина, мы уже неоднократно пользовались обобщенными координатами. Например, положение математического маятника определялось углом отклонения его от вертикали (q = ф 0 и 5ф₂ = 0 (рис. 6.2, б). Работу силы Р₁ вычислим по тому же правилу: 8Д,(Р,) = sin ф,5ф|.

Рис. 6.2, б. К примеру 1: вариация перемещения системы по первой обобщенной координате

Перемещения точек Л/, и М₂ одинаковы (так как при неизменном угле ф₂ второй стержень движется поступательно). Поэтому виртуальная работа силы Р₂ получится из предыдущего выражения заменой масс, т.е. ЪЛ_<(Р₂) = -т$1_х sin ф,5ф|. Откуда

Коэффициент при вариации 5ф, равен обобщенной силе Q_] = — (m, + + m₂)gl_] sin ф,.

3-й способ. Активные силы Р₁₂ консервативны. Найдем потенциальную энергию П, вычислив ее как работу активных сил при перемещении изданного положения в горизонтальное:

Из рассмотренных способов наиболее универсален 2-й.

Из самого определения видно, что обобщенные силы зависят не только от структуры системы и приложенных к ней активных сил, но также и от выбора обобщенных координат.

? Общее уравнение динамики и условия равновесия системы в обобщенных силах

Если преобразовать общее уравнение динамики (5.5) — принцип Лагранжа, учитывая зависимость (6.1) радиусов-векторов точек от обобщенных координат, то получим

или, меняя порядок суммирования,

что по определению обобщенных сил (6.6) дает

Уравнение (6.7) и является общим уравнением динамики/прин- ципом д’Аламбера — Лагранжа, выраженным через обобщенные силы.

Поскольку приращения обобщенных координат 8^ в (6.7) произвольны и независимы друг от друга, то коэффициенты Q, + QJ перед приращениями в полученных уравнениях должны равняться нулю. Если система находится в покое, то все ее точки находятся в покое, т.е. все силы инерции системы, в том числе и обобщенные QJ, равны нулю. Следовательно, условия равновесия системы под действием обобщенных сил принимают вид

В частности, для консервативных сил в целях равновесия системы достаточно потребовать выполнения условий:

? Уравнения Лагранжа второго рода

Общее уравнение динамики в виде (5.6) или (6.7) дает возможность составлять дифференциальные уравнения движения, не содержащие реакции идеальных связей. Для простых систем их применение в такой форме не вызывает затруднений. Но в сложных случаях использование этого уравнения приводит к тяжелым преобразованиям. Поэтому значительно удобнее пользоваться вытекающими из них уравнениями Лагранжа второго рода, в которых трудности преобразований преодолены в общем виде.

Выведем уравнения Лагранжа второго рода из общего уравнения динамики:

или, учитывая (6Л),

Умножим это на (—1) и изменим порядок суммирования:

Разобьем сумму на две части:

или по определению обобщенных сил (6.6):

Далее займемся преобразованиями первого члена под знаком суммы в (*):

Используя определение обобщенных скоростей (6.3), составим частную производную по обобщенной координате:

и полную производную по времени от :

или, учитывая, что смешанные частные производные не зависят от порядка дифференцирования:

Подставляя это выражение в (**) и учитывая (6.4), получим

или по правилам дифференцирования или окончательно

Теперь подставим равенство (***) в уравнение (*):

или, разбивая сумму по к на две части и вынося знак производной за знак суммы:

или по определению кинетической энергии системы

Полученное требование ввиду произвольности и независимости друг от друга вариаций 8^ означает, что квадратные скобки во всех уравнениях должны быть равны нулю, т.е.

Полученная система из s обыкновенных ДУ второго порядка и является уравнениями движения системы в обобщенных координатах, или, как их принято называть, уравнениями Лагранжа второго рода. Число уравнений равно числу СтСв системы.

Если силы, действующие на систему потенциальны, то

И если ввести в рассмотрение функцию Лагранжа/кинетический потенциал L-T— Пи учесть, что , то получим уравнения Лагранжа второго рода для потенциальных сил:

? Задачи на составление уравнений Лагранжа второго рода Методика решений таких задач хорошо разработана. Последовательность рекомендуемых действий такова:

1) изобразить на чертеже все активные силы, действующие на систему, реакции идеальных связей изображать не следует; если имеются силы трения, то их надо включить в число активных сил;
2) определить число СтСв системы и ввести обобщенные координаты q_x__s;
3) вычислить кинетическую Т и потенциальную П энергию системы, выразив их через обобщенные координаты и скорости — Т =
•••) Qsi д >Ql’ «•) Qs ) ^ П П( и учтем, что

Тогда Интегрируя это уравнение, найдем общий интеграл Пусть

н. у. движения таковы, что ф(0) = ф₀, ф(0) = 0. Тогда и окончательно имеем:

Это соотношение можно было получить более простым способом из закона сохранения механической энергии.

? Выражение кинетической энергии через обобщенные координаты и скорости

Кинетическая энергия материальной системы выражается как

Возведем скобку в квадрат и сгруппируем отдельно члены второй степени относительно обобщенных скоростей — квадратичную форму Т₂,

члены первой степени — линейную форму Г, и не содержащие их — нулевую форму Т₀:

где а_ц = a_>i называются коэффициентами инерции. Как видно, коэффициенты а, b зависят от обобщенных координат и времени, но не зависят от обобщенных скоростей. В таких обозначениях

При стационарных связях для движения в инерциальных осях время явно не входит в выражения радиуса-вектора г_р поэтому все частные производные по времени будут равны нулю, и, следовательно, Г, = Т₂, т.е. вся кинетическая энергия системы представляет собой квадратичную форму обобщенных скоростей:

Пример 3. Составить ДУ движения двойного математического маятника в обобщенных координатах (см. пример 1, рис. 6.1).

Решение. Двойной математический маятник имеет две СтСв. За обобщенные координаты возьмем углы q_< = ср, и q₂ — ср₂. Система состоит из двух материальных точек, поэтому ее кинетическая энергия равна

Найдем скорости точек, для чего выразим координаты точек из рис. 6.1: х, = /, cos (р,, у, = /, sin (р,, х₂ = /, cos ср, + /₂ cos ср₂, у, = /, sin ср, + +/₂ sin ф₂. Дифференцируя по времени, получим: х, = /, ф, sin 2 = i 2 + у, 2 = /,ф 2 , V 2 = х 2 + у 2 = / 2 ф 2 + 2/,/₂ С05(ф₂ — ф, )ф,ф, + / 2 ф 2

и кинетическая энергия системы примет вид

Обобщенные силы были найдены в примере 1, поэтому можно перейти к составлению уравнений Лагранжа второго рода.

Для первой обобщенной координаты:

Разделим обе части уравнения на /, и приведем подобные члены, в результате окончательно получим

Для второй координаты уравнение получается аналогичным способом. Интегрирование этих ДУ движения двойного математического маятника связано с большими трудностями, однако если считать углы отклонения малыми, то решение упрощается (см. пример 5 в гл. Д. 7).

Видео:Уравнения Лагранжа второго родаСкачать

iSopromat.ru

Уравнения Лагранжа второго рода, которые представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат.

Для такой системы можно записать s уравнений, которые называются уравнениями Лагранжа второго рода или дифференциальными уравнениями движения в обобщенных координатах:

Уравнения Лагранжа второго рода могут быть обобщены на случай связей, осуществляемых с трением, хотя они и не являются идеальными. Для этого следует силу трения перенести из группы сил реакции в группу активных сил, тогда связь с трением можно формально считать идеальной.

Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат q₁, q₂,…q_s.

Дважды интегрируя эти уравнения и определяя по начальным условиям постоянные интегрирования, получим систему уравнений движения в обобщенных координатах:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах