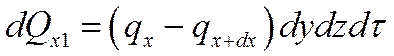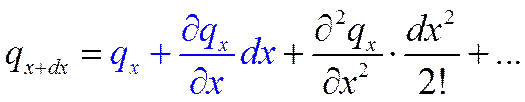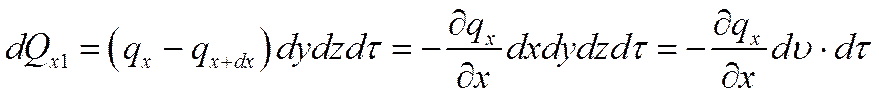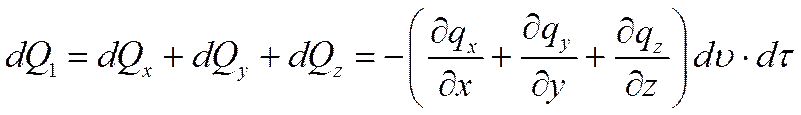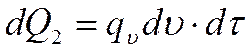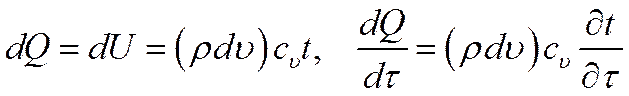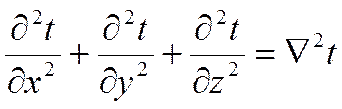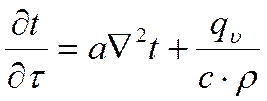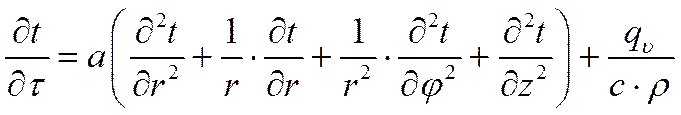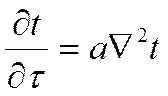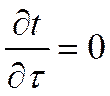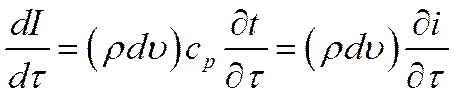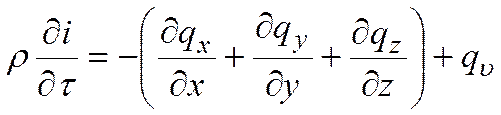Вывод дифференциального уравнения теплопроводности для установившегося и неустановившегося процесса (6 видео)

Дифференциальное уравнение теплопроводности

При решении задач, связанных с нахождением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности.

Температурное поле – совокупность значений температур во всех точках рассматриваемого пространства для каждого момента времени .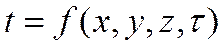

Для упрощения вывода этого дифференциального уравнения сделаны следующие допущения:

– физические параметры постоянны;

– деформация рассматриваемого объема, связанная с изменением температуры, является очень малой величиной по сравнению с самим объемом;

– внутренние источники теплоты в теле 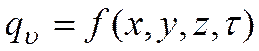распределены равномерно.

В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии в формулировке:

количество теплоты dQ, введенное в элементарный объем извне за время dτ теплопроводностью, а также от внутренних источников, равно изменению внутренней энергии или энтальпии вещества (в зависимости от рассмотрения изохорного или изобарного процесса), содержащегося в элементарном объеме.

(*)

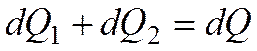
где dQ₁ – количество теплоты, Дж, введенное в элементарный объем теплопроводностью за время dτ;

dQ₂ – количество теплоты, Дж, которое за время dτ выделилось в элементарном объем 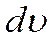за счет внутренних источников;

dQ – изменение внутренней энергии или энтальпии вещества, содержащегося в элементарном объеме 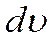, за время dτ.

Для нахождения составляющих выделим в теле элементарный параллелепипед со сторонами dx, dy, dz. Параллелепипед расположен так, чтобы его грани были параллельны соответствующим координатным плоскостям.

Количество теплоты, которое подводится к граням элементарного объема за время dτ в направлении осей Оx, Оy, Оz обозначим соответственно dQ_x, dQ_y, dQ_z.

Количество теплоты, которое будет отводиться через противоположные грани в тех же направлениях, обозначим соответственно dQ_x₊_dx, dQ_y₊_dy, dQ_z₊_dz.

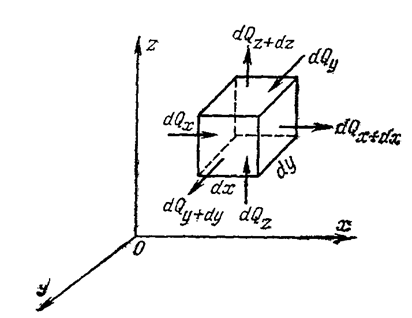
Количество теплоты, подведенное к грани dydz=dF в направлении оси Ох за время dτ, составляет ,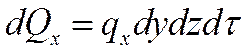

где q_x – проекция плотности теплового потока на направление нормали к указанной грани.

Количество теплоты, отведенное через противоположную грань элементарного параллелепипеда в направлении оси Ох

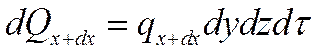
Разница количеств теплоты, подведенного к элементарному параллелепипеду и отведенного от него за время dτ в направлении оси Ох

Функция 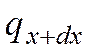является непрерывной в рассматриваемом интервале dx и может быть разложена в ряд Тейлора

Если ограничиться двумя первыми членами ряда:

Аналогично можно найти количество теплоты, подводимое к элементарному объему в направлениях двух других координатных осей Oy и Oz.

Количество теплоты dQ, подводимое теплопроводностью к рассматриваемому объему, будет равно

Обозначим через 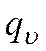, Вт/м 3 , количество теплоты, выделяемое внутренними источниками в единице объема в единицу времени.

Тогда

Третья составляющая уравнения (*) найдется в зависимости от характера термодинамического процесса изменения системы.

В случае рассмотрения изохорного процесса вся теплота, подведенная к элементарному объему, уйдет на изменения внутренней энергии вещества, заключенного в этом объеме, т.е.

где 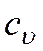– изохорная теплоемкость единицы массы, Дж/(кг·К);

ρ – плотность вещества, кг/м 3 .

Подставляя полученные выражения в уравнение (*), получим

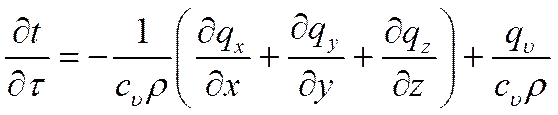
Проекции вектора плотности теплового потока на координатные оси Ох, Оу, Оz определяются законом Фурье:

; ; .

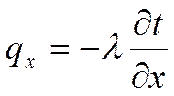
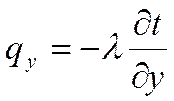
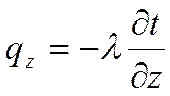
где λ – коэффициент теплопроводности (физический параметр вещества, характеризующий способность проводить теплоту), Вт/(м∙°С).

Подставляя полученные выражения проекций вектора плотности теплового потока в уравнение (*), опуская индекс при с, ипринимая теплофизические характеристики постоянными, получим

(***)

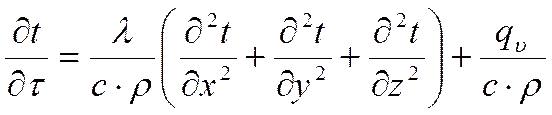
Выражение (***) называется дифференциальным уравнением теплопроводности. Оно устанавливает связь между временнЫм и пространственным изменением температуры в любой точке тела.

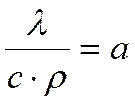
Тогда выражение (***) имеет вид:

Выражение (***) в цилиндрической системе координат:

где r – радиус-вектор;

φ – полярный угол;

Коэффициент пропорциональности а, м 2 /с, называется коэффициентом температуропроводности и является физическим параметром вещества.

Он характеризует скорость изменения температуры, т.е. является мерой теплоинерционных свойств тела. Поэтому при прочих равных условиях выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое обладает бόльшим коэффициентом температуропроводности.

Коэффициент температуропроводности зависит от природы вещества.

Например, жидкости и газы обладают большой тепловой инерционностью и, следовательно, малым коэффициентом температуропроводности.

Металлы обладают малой тепловой инерционностью, т.к. они имеют большой коэффициент температуропроводности.

Если система тел не содержит внутренних источников теплоты (q_υ=0), то

Если имеются внутренние источники теплоты, но температурное поле соответствует стационарному состоянию, т.е. 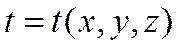, то

При рассмотрении изобарного процесса вся теплота, подведенная к объему, уйдет на изменение энтальпии вещества, заключенного в этом объеме:

(**)

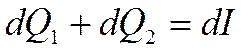
Если рассматривать энтальпию единицы объема как 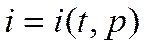, то

где с_p – изобарная теплоемкость единицы массы, Дж/(кг·К).

В итоге (**) имеет вид:

\|	следующая лекция ==>
СПОСОБЫ ПЕРЕНОСА ТЕПЛОТЫ	\|	Условия однозначности для процессов теплопроводности. Дифференциальное уравнение теплопроводности описывает явление теплопроводности в самом общем виде

Дата добавления: 2016-02-09 ; просмотров: 4650 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Дифференциальное уравнение теплопроводности
Дифференциальные уравнения теплопроводности и конвективного теплообмена
18 Дифференциальные уравнения
18.2 Распределение температур в однослойной
плоской стенке
18.3 Теплопроводность при нестационарном режиме
18.5 Условия гидродинамического подобия
18.6 Тепловое подобие
📺 Видео

Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать

Дифференциальное уравнение теплопроводности

Изучение любого физического процесса связано с установлением зависимости между величинами, характеризующими данный процесс. Для сложных процессов, к которым относится передача теплоты теплопроводностью, при установлении зависимостей между величинами удобно воспользоваться методами математической физики, которая рассматривает протекание процесса не во всем изучаемом пространстве, а в элементарном объеме вещества в течение бесконечно малого отрезка времени. Связь между величинами, участвующими в передаче теплоты теплопроводностью, устанавливается дифференциальным уравнением теплопроводности. В пределах выбранного элементарного объема и бесконечно малого отрезка времени становится возможным пренебречь изменением некоторых величин, характеризующих процесс.

При выводе дифференциального уравнения теплопроводности принимаются следующие допущения:

• внутренние источники теплоты отсутствуют;
• среда, в которой распространяется тепло, однородна и изотропна;
• используется закон сохранения энергии, который для данного случая формулируется следующим образом: разность между количеством теплоты, вошедшей вследствие теплопроводности в элементарный параллелепипед за время dt и вышедшей из него за то же время, расходуется на изменение внутренней энергии рассматриваемого элементарного объема.

Выделим в среде элементарный параллелепипед с ребрами dx, dy, dz (рис. 4.2). Температуры граней различны, поэтому через параллелепипед проходит теплота в направлении осей х, у, z. Через площадку dxdy за время dt согласно уравнению Фурье проходит количество теплоты

(gradГ взят в виде частной производной, так как предполагается зависимость температуры не только от х, но и от других координат и времени).

Через противоположную грань на расстоянии dz отводится количество теплоты, определяемое из выражения

где — температура второй грани, а величина определяет

изменение температуры в направлении Z-

Рис. 4.2. Схема распространения тепла к выводу дифференциального уравнения теплопроводности

Последнее уравнение можно представить в другом виде:

Итак, приращение внутренней энергии в параллелепипеде за счет потока тепла в направлении оси z равно

Приращение внутренней энергии в параллелепипеде за счет потока тепла в направлении оси у выразится аналогичным уравнением

а в направлении оси х

Полное приращение внутренней энергии в параллелепипеде

С другой стороны, согласно закону сохранения энергии

где dxdydz — объем параллелепипеда; dxdydzp — масса параллелепипеда; с — удельная теплоемкость среды; р— плотность среды; — изменение

температуры в данной точке среды за время dt.

Левые части уравнений (4.19) и (4.20) равны, поэтому

или

и обычно обозначают сокращенно V 2 ; величину называют тем

пературопроводностью и обозначают буквой а. При указанных обозначениях дифференциальное уравнение теплопроводности принимает вид

Уравнение (4.23) называется дифференциальным уравнением теплопроводности (или дифференциальным уравнением Фурье) для трехмерного нестационарного температурного поля при отсутствии внутренних источников теплоты. Оно является основным при изучении вопросов нагревания и охлаждения тел в процессе передачи теплоты теплопроводностью и устанавливает связь между временным и пространственным изменениями температуры в любой точке поля.

Температуропроводность является физическим параметром вещества и имеет единицу м 2 /с. В нестационарных тепловых процессах а характеризует скорость изменения температуры.

Из уравнения (4.23) следует, что изменение температуры во

времени для любой точки тела пропорционально величине а.

Поэтому при одинаковых условиях быстрее увеличивается температура у того тела, которое имеет большую температуропроводность.

Дифференциальное уравнение теплопроводности с источником теплоты внутри тела имеет вид

где q_y— удельная мощность источника, т.е. количество выделяемой теплоты в единице объема вещества за единицу времени.

Это уравнение записано в декартовых координатах. В других координатах оператор Лапласа имеет иной вид, поэтому меняется и вид уравнения. Например, в цилиндрических координатах дифференциальное уравнение теплопроводности с внутренним источником теплоты

где г — радиус-вектор в цилиндрической системе координат; ф — полярный угол.

Видео:Вывод уравнения теплопроводностиСкачать

Дифференциальные уравнения теплопроводности и конвективного теплообмена

18 Дифференциальные уравнения

теплопроводности и конвективного

18.1 Дифференциальное уравнение теплопроводности

В соответствии с первым законом термодинамики теплота, передаваемая твёрдому телу из окружающей среды, при отсутствии работы деформации полностью трансформируется во внутреннюю энергию тела.

Уравнение теплового баланса для элемента с величиной рёбер (рисунок 18.1) в однородном твёрдом теле имеет вид:

, (18.1)

где — элементарная теплота, передаваемая через грани выделенного элемента в направлении осей x, y,z ; dU — изменение внутренней энергии элемента.

В направлении оси x через грань dydz за время dt поступает в соответствии с законом Фурье теплота

За то же время через противоположную грань, расположенную на расстоянии dx от первой и имеющую температуру , из элемента передается теплота

Результирующая теплота, подведенная теплопроводностью к элементу в направлении оси х, равна

(18.2)

Аналогично определяется результирующая теплота в направлении осей y и z :

(18.3)

Изменение внутренней энергии элемента составляет

(18.4)

C учетом (18.2-18.4) уравнение (18.1) имеет вид:

(18.5)

После сокращений в уравнении (18.5) получается:

(18.6)

Выражение (18.6) называют дифференциальным уравнением теплопроводности. Его записывают и в таком виде:

, (18.7)

где — коэффициент температуропроводности, характеризующий темп изменения температуры;

— оператор Лапласа.

Уравнение (18.7) описывает в самом общем виде процесс теплопроводности и устанавливает связь между временными и пространственными изменениями температуры тела. Для его решения применительно к определенной задаче необходимо математическое описание конкретных условий, называемых условиями однозначности, которые включают:

временные или начальные условия, определяющие распределение температуры в теле в начальный момент;

геометрические условия, характеризующие форму и размеры тела;

физические условия, задаваемые теплофизическими параметрами вещества, составляющего рабочее тело;

граничные условия, определяющие характер взаимодействия тела с окружающей средой на границе соприкосновения.

Начальные условия имеют смысл при нестационарной теплопроводности и обычно задаются законом распределения температур по всему объему тела для момента времени t = 0.

Граничные условия могут быть заданы несколькими способами.

Если для любого момента времени известно распределение температур на границе тела, то это называют граничными условиями первого рода.

При граничных условиях второго рода задаётся поверхностная плотность теплового потока (а, следовательно, и температурный градиент) в каждой точке поверхности тела для любого момента времени. Температура на поверхности тела при этом неизвестна.

Граничные условия третьего рода предполагают, что известна температура окружающей среды и закономерность взаимосвязи между этой температурой и температурой тела. В условиях конвективного теплообмена связующим является уравнение Ньютона-Рихмана.

Решение дифференциального уравнения теплопроводности совместно с условиями однозначности позволяет получить температурное поле исследуемого тела для любого частного случая в любой момент времени. Такое аналитическое решение позволяет в ряде случаев избавиться от проведения сложных и дорогостоящих экспериментальных работ.

18.2 Распределение температур в однослойной

плоской стенке

Пусть теплота передается через плоскую стенку (рисунок 15.2а) толщиной d. Размеры стенки в направлении осей о-z и o-y не ограничены. Тепловой поток постоянный и не зависит от времени. Температура горячей поверхности стенки равна , температура холодной поверхности — .

Для этого случая одномерной задачи уравнение теплопроводности (18.7) имеет вид:

(18.8)

При принятых граничных условиях первого рода () последовательное интегрирование формулы (18.8) даёт:

(18.9)

Выражение (18.9) показывает линейную зависимость температуры по толщине стенки.

Для определения констант интегрирования используются граничные условия:

После подстановки констант в формулу (18.9) выражение для определения температуры в любом сечении стенки предстанет в таком виде:

, (18.10)

где x — отстояние сечения от начала координат

18.3 Теплопроводность при нестационарном режиме

Нестационарные процессы теплопроводности встречаются при нагревании и охлаждении металлических заготовок в литейном и кузнечном производствах, при обжиге кирпича, при запуске дизельных дизельных или карбюраторных двигателей, при прогреве холодных зданий, при замерзании рек и водохранилищ и т. д.

Как отмечалось в п 15.1 , нестационарная теплопроводность характеризуется уравнением

Указанная зависимость может быть определена из решения дифференциального уравнения теплопроводности (18.6) при граничных условиях третьего рода методами теории подобия.

Для одномерной нестационарной задачи изменение температуры по оси х и во времени определяется выражением, полученным из уравнения теплопроводности (18.7), которое для этого случая имеет вид:

Обработка этого выражения методами теории подобия выявляет число Фурье:

(18.11)

Обработка уравнения (18.11) , характеризующего граничные условия третьего рода, выявляет число подобия Био:

где l — характерный линейный размер геометрической системы, λ – теплопроводность стенки.

Число Био отличается от числа Нуссельта тем, что оно содержит теплопроводность материала тела, а не теплопроводность движущейся около тела жидкой или газообразной среды. Это число определяет соотношение теплоты, переданной конвективным способом, и теплоты, переданной внутри тела теплопроводностью.

Искомая функция в виде безразмерной температуры определяется в общем случае выражением

. (18.12)

В качестве примера ниже рассматривается процесс охлаждения равномерно прогретой пластины с начальной температурой t , которая омывается с обеих сторон жидкостью или газом с температурой при коэффициенте теплоотдачи a. Размеры пластины в направлении осей y и z считаются неограниченными, а физические характеристики материала пластины — теплопроводность l, теплоёмкость с и плотность r — постоянными.

Решение задачи представляется в виде:

(18.13)

где — температуры на поверхности и в центральном сечении пластины.

Отсутствие в формулах (18.13) линейного симплекса объясняется тем, что в средней плоcкости и на поверхности пластины температуры постоянны и изменяются только в направлении оси x.

Теплота, передаваемая пластиной в окружающую среду за время t, равно изменению внутренней энергии пластины за период охлаждения.

Начальная внутренняя энергия пластины, отсчитанная от внутренней энергии при температуре среды как от нуля, равна

(18.14)

Отношение теплоты, переданной за период t, к начальной внутренней энергии пластины определяется также безразмерными числами Био и Фурье:

(18.15)

Конкретные решения уравнений (18.13,18.15) обычно представлены в виде графиков или в табличной форме (cм. таблицу 18.1). При решении конкретной задачи вначале подсчитывают числовые значения определяющих критериев, а затем, пользуясь таблицей, находят искомые значения.

Решения, аналогичные вышеизложенному, имеются для других геометрических систем — цилиндрических тел, шаров и др.

Таблица 18.1 — Расчётные зависимости для пластины

18.4 Дифференциальные уравнения конвективного

Дифференциальные уравнения конвективного теплообмена учитывают особенности гидродинамики потока и влияние различных факторов на теплообмен между потоком и поверхностью твердого тела.

Гидродинамика потока описывается уравнением движения вязкой жидкости (уравнением Навье-Стокса) и уравнением неразрывности (сплошности) потока.

Уравнение движения учитывает влияние сил инерции (левая часть

уравнения), сил вязкостного трения (третье слагаемое в правой части), сил статического давления (второе слагаемое в правой части) и гравитационных сил (первое слагаемое в правой части). Оно определяет поле скоростей во времени, а также в пространстве, и в проекции на ось х имеет следующий вид:

где выделенное скобками в левой части выражение представляет собой полную или субстанциальную (в пространственных и временных координатах) производную от скорости . С учетом этого

(18.16а)

Аналогично записываются уравнения в проекции на оси y и z:

(18.16б)

(18.16в)

В формулах (18.16): r — плотность вязкой жидкости, — проекции скорости на соответствующие оси x, y и z , p — давление, m — коэффициент динамической вязкости.

Уравнение сплошности выводится на основе закона сохранения массы и говорит о том, что в любом сечении неразрывного потока жидкости или газа массовый расход имеет одно и то же значение:

(18.17)

В основу вывода дифференциального уравнения энергии для движущегося потока сжимаемой вязкой жидкости положен закон сохранения энергии. Это уравнение определяет изменение температуры жидкости во времени и в пространстве. В отличие от дифференциального уравнения теплопроводности в уравнении энергии учитывается то обстоятельство, что в движущемся потоке температура изменяется не только за счет нагревания или охлаждения, но и в связи с изменением положения этой жидкости в пространстве. Этим объясняется появление в правой части формулы (18.19) субстанциальной производной от скорости:

(18.19)

Дифференциальное уравнение, описывающее процесс теплообмена на границе жидкости и стенки (16.3) , уже было применено ранее в п. 16.2.

18.5 Условия гидродинамического подобия

Для двух подобных систем, в которых протекают подобные процессы, записываются уравнения движения

(18.20)

Для подобных процессов

Если выразить переменные второй системы через переменные первой системы и множители подобного преобразования, то получится

(18.21)

Тождественность уравнений (18.20) и (18.21) возможно при следующем условии:

Из равенства получается индикатор подобия и число гомохронности

Из условия получается индикатор подобия , которому соответствует число Фруда

Следующее равенство даёт индикатор подобия и число Эйлера

Из условия следует индикатор подобия и число Рейнольдса

где — кинематическая вязкость.

Из полученных чисел подобия определяющим в гидродинамических задачах является число Эйлера

(18.22)

Для стационарных гидродинамических процессов, когда фактор времени не имеет значения, выражение (18.22) упростится

(18.23)

При естественной конвекции скорость потока определить чрезвычайно сложно, поэтому часто число Фруда преобразуют в более удобное число Грасгофа, которое равно произведению числа Фруда на квадрат числа Рейнольдса и отношение плотностей свободно движущейся среды:

, (18.24)

где b — температурный коэффициент объемного расширения жидкости.

Замена отношения плотностей произведением температурного объемного коэффициента на разность температур объясняется тем, что причиной естественной конвекции является разность плотностей жидкости, которая образуется из-за изменения температуры.

Анализ уравнения сплошности (18.17) показывает, что новых чисел подобия, кроме тех, что получены из уравнений энергии, движения и теплообмена, это выражение не дает.

18.6 Тепловое подобие

Ранее, в главе 16, было показано, что из дифференциального уравнения, описывающего процесс теплообмена на границе между жидкостью и стенкой, получается число Нуссельта