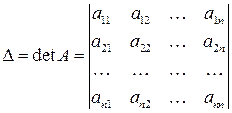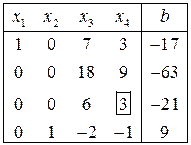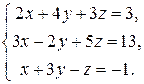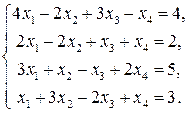Содержание:
- Матрицы и системы линейных уравнений. Матричная запись системы линейных уравнений
- Обратная, вырожденная и невырожденная матрицы
- Метод Жордана-Гаусса решения матричных уравнений
- Пример №26
- Решение системы с помощью обратной матрицы
- Пример №27
- Решение произвольных систем линейных уравнений
- Определение ранга матрицы. Вырожденные и невырожденные матрицы. Матричная запись системы линейных уравнений
- 💥 Видео
Матрицы и системы линейных уравнений. Матричная запись системы линейных уравнений
Одно из важных применений матриц связано с системами линейных уравнений. Рассмотрим систему

и соответствующие ей матрицы
Тогда систему (1) можно заменить единственным уравнением АХ = В.
Уравнение (2) называют матричной записью системы (1). Например, система
в матричной записи выглядит так:
Заметим, что матричную запись систем линейных уравнений применяли древнекитайские математики во 
Обратная, вырожденная и невырожденная матрицы
Рассмотрим вопросы, связанные с умножением квадратных матриц порядка 
и говорили о том, что для любой квадратной матрицы А выполняется свойство АЕ = ЕА = А.
Известно, что любого числа 


Нечто подобное имеет место и для квадратных матриц, причем роль условия 
Определение 1. Пусть А — квадратная матрица порядка 


Для обратных матриц выполняется свойство: 
Заметим, что строки матрицы А — это арифметические векторы из 
Определение 2. Квадратная матрица А называется невырожденной, если ее строки линейно независимы, и вырожденной в противном случае.
В лекции 1 мы указывали, что линейно независимая система векторов не может содержать нулевой вектор. Т.о., в невырожденной матрице не может быть нулевых строк. Над строками матрицы можно совершать элементарные преобразования:
1) переставлять строки;
2) вычеркивать нулевую строку;
3) умножать строку на число 
4) прибавлять к одной из строк другую строку, умноженную на любое число. Заметим, что речь идет о тех же самых элементарных преобразованиях, которые используются в методе Гаусса, с той лишь разницей, что теперь это строки матрицы, а не уравнения системы.
Теорема 1. Если над строками невырожденной матрицы А проделать элементарные преобразования, то получим снова невырожденную матрицу.
Теорема 2. Для любой невырожденной матрицы А существует обратная матрица 
Метод Жордана-Гаусса решения матричных уравнений
Рассмотрим матричное уравнение

где А и В — две данные матрицы, X — искомая матрица. Существенно, что А — квадратная матрица порядка 
Эффективным методом решения матричных уравнений (3) является метод полного исключения Жордана-Гаусса.
Метод Жордана-Гаусса. Пусть А — невырожденная матрица. Припишем к ней (например, справа) матрицу В и далее будем работать уже со «сдвоенной» матрицей:
Если, выполняя элементарные преобразования над строками этой матрицы, привести ее левую часть к единичной матрице 
В частном случае, когда нужно найти обратную матрицу 

Пример №26
Методом Жордана-Гаусса для матрицы
найти обратную матрицу
Решение:
Составим «сдвоенную» матрицу
С помощью элементарных преобразований приведем ее левую часть к единичной матрице 
Правее вертикальной черты получилась обратная матрица 
Замечание 1. При нахождении обратной матрицы методом Жордана-Гаусса возможны вычислительные ошибки. Поэтому желательно делать проверку:

Решение системы с помощью обратной матрицы
Рассмотрим произвольную систему 

Запишем эту систему 
Теорема 3. Пусть квадратная матрица А является невырожденной. Тогда решением матричного уравнения АХ = В будет

Доказательство. Используя очевидные преобразования, получим

Замечание 2. Результат, полученный при доказательстве теоремы 3, часто называют методом обратной матрицы.
Пример №27
Решить систему методом обратной матрицы:
Решение:
Этой системе соответствуют матрицы:
Подобно тому, как это делалось в примере 1, найдем обратную матрицу к матрице А:
Используя теорему 3, получим
Итак, наша система имеет решение: 
Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:
| Высшая математика: полный курс лекций |
Другие темы которые вам помогут понять высшую математику:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Неоднородная система линейных уравненийСкачать

Решение произвольных систем линейных уравнений
Тема 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
1. Матрицы. Сложение матриц; умножение матрицы на число; произведение матриц. Обратная матрица.
2. Определители n-го порядка и их свойства. Методы вычисления определителей.
3. Обратная матрица.
5. Решение невырожденных систем линейных уравнений.
6. Теорема Кронекера – Капелли. Решение произвольных линейных систем.
Решение невырожденных систем линейных уравнений
Пусть задана система линейных уравнений

где 


Решением системы (1.1) называется такое множество значений неизвестных 
Система уравнений, имеющая хотя бы одно решение, называется совместной, а система, не имеющая решений – несовместной.

называются матрицей системы и расширенной матрицей системы соответственно.
Рассмотрим случай, когда число уравнений m системы совпадает с числом неизвестных n (m = n). Тогда матрица системы А является квадратной матрицей порядка n.
Система n уравнений с n неизвестными называется невырожденной, если определитель матрицы системы А отличен от нуля ( 
Невырожденная система имеет единственное решение. Существует два метода решения таких систем.
1. Правило Крамера. Если определитель Δ отличен от нуля, то решение системы находится по формулам

где 
2. Матричный метод. Введем матрицу столбец свободных членов системы 

Тогда систему n уравнений с n неизвестными можно записать в виде

Эта форма записи системы называется матричной.
Матрицей 


где Е – единичная матрица n-го порядка.
Матрица, определитель которой не равен нулю, называется невырожденной.
Для того чтобы данная матрица имела обратную, необходимо и достаточно, чтобы она была невырожденной.
Рассмотрим уравнение (1.3). Пусть А – невырожденная матрица. Тогда решение системы можно найти по формуле

Пример 1.1. Проверить невырожденность системы линейных уравнений 
Решение. Запишем матрицу системы 

Так как 
а) по формулам Крамера.

По формулам (1.2) находим решение системы:
Делаем проверку: 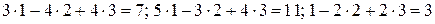
б) матричным методом.
Находим обратную матрицу

где 




где 




По формуле (1.4) находим решение:

Ответ: 
Решение произвольных систем линейных уравнений
Рассмотрим произвольную систему линейных уравнений (1.1).
Элементарными преобразованиями матрицы называются:
а) перестановка местами любых двух строк;
б) умножение строки на некоторое число 
в) прибавление к одной строке матрицы любой другой строки, умноженной на некоторое число;
г) удаление нулевой строки.
Решение системы методом Жордана–Гаусса основано на следующем утверждении: элементарные преобразования расширенной матрицы системы не изменяют множества решений системы.
Суть метода заключается в том, чтобы при помощи элементарных преобразований привести расширенную матрицу к наиболее простому виду.
С помощью операции в) можно исключить какое-либо неизвестное из всех уравнений, кроме одного.
Переменная 


Матрица системы с помощью элементарных преобразований приводится к так называемому базисному виду, если в каждом уравнении системы есть базисная переменная.
Если матрица системы приведена к базисному виду, то переменные, не являющиеся базисными, называются свободными.
Решение системы, полученное после приравнивания нулю всех свободных переменных, называется базисным.
Опишем одну итерацию метода Жордана–Гаусса.
В первой строке расширенной матрицы находим ненулевой элемент 


Элемент 
Если 


После этой операции коэффициент при 

Описанную итерацию проводим для остальных строк расширенной матрицы, пока не получим m базисных неизвестных ( в каждом уравнении – по одной базисной переменной).
После этого находим общее решение и базисное (приравнивая свободные неизвестные нулю).
Пример 1.2. Решить систему линейных уравнений
методом Жордана–Гаусса. Найти общее и базисное решения.
Решение. Вычисления будем производить в таблице. В исходной части таблицы записываем расширенную матрицу системы.
В первой строке выберем элемент 

Выбираем элемент 
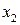
Выбираем, например, элемент 

Теперь делаем нули в остальных строках четвертого столбца. Получаем таблицу, в которой переменная 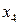
Удаляем вторую нулевую строку, получаем таблицу

Поскольку каждое уравнение теперь содержит по одной базисной переменной, то оставшаяся небазисная переменная 
Полагаем 

Из второй строки следует 


Из первой строки следует 


Выписываем общее решение: 
Найдем базисное решение. Положим 

Сделаем проверку, подставляя найденное решение в исходную систему
Ответ. Общее решение: 

Задание 1. Проверить невырожденность системы линейных уравнений и решить ее: а) по формулам Крамера; б) матричным методом.
1.1. 

1.4. 

1.7 

1.10. 
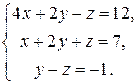
1.13. 

1.16. 
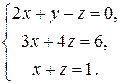
1.19. 

1.22. 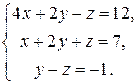

1.25. 
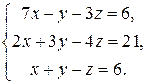
1.28. 

Задание 2. Решить систему линейных уравнений методом Жордана–Гаусса. Найти общее и базисное решения.
2.1. 
2.3. 
2.5. 
2.7. 
2.9. 
2.11. 
2.13. 
2.15. 
2.17. 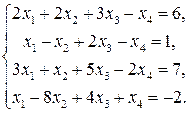
2.19. 
2.21. 
2.23. 
2.25. 
2.27. 
2.29. 
Видео:Вырожденные и невырожденные однородные линейные системы. ТемаСкачать

Определение ранга матрицы. Вырожденные и невырожденные матрицы. Матричная запись системы линейных уравнений
Определение матрицы. Понятие подматрицы. Операции над матрицами и их свойства.
Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов. Числа составляющие матрицу называются элементами матрицы. Подматрицей матрицы А является матрица, которая состоит из невычеркнутых элементов первоначальной матрицы.
Операции над матрицами:
· Транспонирование – переход от матрицы А к матрице А Т , в которой строки и столбцы поменялись местами с сохранением порядка.
· Сложение матриц. Они должны быть одинаковой размерности и одноимённые элементы складываются.
· Умножение матриц на число.
· Вычитание матриц. А-В=А=(-1)В
· Умножение матриц. Правило умножения: Произведением матриц АВ называется такая матрица С каждый элемент которой равен сумме произведений элементов итой строки матрицы А на элементы житого столбца матрицы В.
Деления в матрицах нет!
· А Т *(В+С)= А Т *В+ А Т *С
· А*Е(единичная матрица)=А или Е*А=А
· А*(В*С)=(А*В)*С главное порядок
Понятие определителя квадратной матрицы порядка n. Свойства определителей. Методы вычисления определителей. Примеры.
Определитель – число, характеризующее квадратную матрицу.
Вырожденная матрица – определитель = 0
Невырожденная матрица – определитель ≠ 0
Определитель матрицы первого порядка = элементу этой матрицы.
Определитель матрицы второго порядка, называется число которое вычисляется по формуле:
Определитель матрицы третьего порядка, называется число которое вычисляется по формуле (правило треугольника или правило Саррюса):
Определители n-го порядка
Теорема: Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраическое дополнение.
Это метод вычисления определителей, и его называют метод разложения по элементам какой-либо строки или какого-либо столбца.
Определитель диагональной матрицы = произведению элементов главной диагонали.
· Если какая-нибудь строка (столбец) состоит только из нулей, то её определитель равен нулю.
· Если все элементы какой-либо строки (столбца) умножить на число, то и весь определитель умножается на число.
· При транспонировании матрицы её определитель не изменится.
· При перестановке двух строк или столбцов матрицы, её определитель меняет знак на противоположный.
· Если квадратная матрица содержит две одинаковые строки или столбца, то её определитель будет равен нулю.
· Если элементы двух строк (столбцов) матрицы пропорциональны, то её определитель будет равен нулю.
· Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраическое дополнение элементов другой строки или столбца этой матрицы равна нулю.
· Определитель матрицы не изменится если к элементам какой-либо строки или столбца матрицы прибавить элементы другой строки (столбца) предварительно умноженное на одно и тоже число. Получаем нули.
· Определитель произведения двух матриц равен произведению двух определителей.
Определение обратной матрицы. Теорема о необходимом и достаточном условии существования обратной матрицы. Вычисление обратной матрицы (на примере).
Обратная матрица — такая матрица A −1 , при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Алгоритм вычисления обратной матрицы:
Определение ранга матрицы. Вырожденные и невырожденные матрицы. Матричная запись системы линейных уравнений.
Рангматрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Вырожденная матрица – определитель = 0
Невырожденная матрица – определитель ≠ 0
Матричная запись системы линейных уравнений:
💥 Видео
Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Совместные и несовместные, определенные и неопределенные системы линейных уравненийСкачать

Вырожденные и невырожденные однородные линейные системы. ОтветыСкачать

Решение системы уравнений методом Крамера 2x2Скачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Матричный метод решения систем уравненийСкачать

Видеоурок "Однородные системы линейных уравнений"Скачать

Решение систем линейных алгебраических уравнений методом Крамера.Скачать

Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Вырожденные и невырожденные однородные линейные системы. ВопросыСкачать