Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
- Описание и исходные данные задания, 50% решения + фотография:
- Вынужденные колебания описываются дифференциальным уравнением
- Условие
- Ответ
- Решение
- Вынужденные колебания
- Определение вынужденных колебаний
- Дифференциальное уравнение вынужденных колебаний
- Резонанс вынужденных колебаний
- Примеры задач с решением
- 🎦 Видео
Описание и исходные данные задания, 50% решения + фотография:
№1 1.88. Вынужденные колебания описываются дифференциальным уравнением 0,4 + 0,48 + 1,6x = 0,8 sin3t. Определить: частоту вынужденных колебаний; частоту собственных колебаний системы; при какой частоте внешней силы будет наблюдаться резонанс.
Круговая частота вынужденных колебаний равна коэффициенту при , стоящему под знаком синуса в правой части дифференциального уравнения: рад/с. Разделим дифференциальное уравнение вынужденных колебаний на 0,4: . Коэффициент при есть квадрат круговой частоты собственных колебаний системы, следовательно: рад/с. Связь между резонансной и собственной круговыми частотами системы: , где – коэффициент затухания колебаний. Выразим отсюда : ;
| Если вам нужно решить физику, тогда нажмите ➔ заказать контрольную работу по физике. |
| Похожие готовые решения: |
- В стальном стержне распространяется плоская продольная волна от источника, уравнение колебаний которого задано в виде: x = 10-5 sin102t, м. Модуль Юнга стали 2•1011 Н/м2; плотность стали 8•103 кг/м3. Написать уравнение волны. Определить длину волны.
- Тело, совершая затухающие колебания, за время t = 50 с потеряло 60 % своей энергии. Определить коэффициент затухания ß.
- Уравнение движения гармонического колебания имеет вид: x = 0,02 cosпt. Постройте график зависимости x(t). Найти смещение через 0,25 с; через 1,25 с. Ответы пояснить с помощью графика.
- Точка совершает гармонические колебания с амплитудой 10 см и периодом 2 с. Написать уравнение этих колебаний, считая, что при t = 0 смещение равно нулю. Определить также фазу для двух моментов времени: а) когда смещение точки равно 6 см; б) когда скорость точки равна 10 см/с.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:71. Вынужденные колебанияСкачать

Вынужденные колебания описываются дифференциальным уравнением
- Реферат.Справочник
- Контрольные работы по физике
- Вынужденные колебания описываются дифференциальным уравнением
Условие
Вынужденные колебания описываются дифференциальным уравнением . Определить частоту вынужденных колебаний, частоту собственных колебаний системы, при какой частоте внешней силы будет наблюдаться резонанс. Дано: Найти:
Ответ
— частота собственных колебаний системы, — частота вынужденных колебаний системы, резонанс возникает, если частота внешней силы приближается к собственной частоте: .
Решение
Дифференциальное уравнение вынужденных колебаний имеет вид
Приведём к такому виду заданное дифференциальное уравнение:
После сравнения, получаем: — коэффициент затухания, — частота собственных колебаний системы, — внешняя периодическая сила, — частота внешней периодической силы.
Частота вынужденных колебаний системы вычисляется по формуле:
Резонанс возникает, если частота внешней силы приближается к собственной частоте: .
Ответ: — частота собственных колебаний системы, — частота вынужденных колебаний системы, резонанс возникает, если частота внешней силы приближается к собственной частоте: .
Видео:Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать

Вынужденные колебания
Видео:Вынужденные колебания. Резонанс | Физика 11 класс #9 | ИнфоурокСкачать

Определение вынужденных колебаний
Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.
Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.
Видео:Лекция №11 "Вынужденные колебания" (Попов П.В.)Скачать

Дифференциальное уравнение вынужденных колебаний
Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:
Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:
где $x$ — координата; $delta $ — коэффициент затухания; $_0$ — циклическая частота свободных незатухающих колебаний (если $delta $=0, то $_$называют собственной частотой колебаний).
Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:
где $q$ — заряд; $delta =frac$ — коэффициент затухания; $_0=frac<sqrt>$; $U=U_m$ — внешнее переменное напряжение.
Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:
где $s$ — колеблющийся параметр; $x_0=frac$ если колебания механические ($x_0=frac— в случае электрических колебаний$).
Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:
Его общее решение:
где $A_0$ — начальная амплитуда колебаний.
Частное решение уравнения (4) в представлено выражением:
Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).
Установившись, вынужденные колебания происходят с частотой $omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $omega $.
Видео:Затухающие колебания. Вынужденные колебания | Физика 9 класс #26 | ИнфоурокСкачать

Резонанс вынужденных колебаний
Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.
Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(omega )$. Взяв производную $frac$ и приравняв ее к нулю получим:
Равенство (10) справедливо при:
Получается, что резонансная частота ($_r$) равна:
При $^2ll ^2_0$ резонансная частота совпадает с собственной частотой колебаний $_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:
При небольшом затухании колебаний (если $^2ll ^2_0$) амплитуда при резонансе равна:
где $Q=frac<_0>$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Примеры задач с решением
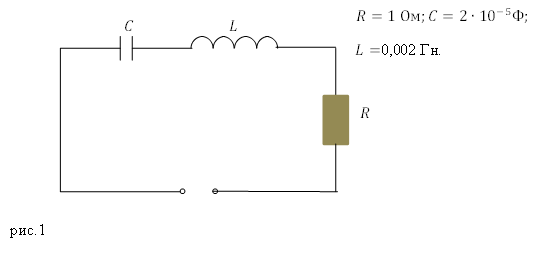
Задание. Какова добротность колебательного контура, представленного на рис.1?
Решение. Добротность электрического колебательного контура найдем как:
При этом собственная частота колебаний в таком контуре равна:
коэффициент затухания находим как:
Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:
Ответ. $Q=10$
Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?
Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:
где коэффициент затухания равен $delta =frac$. Из функции, которая задает вынуждающую силу:
мы видим, что амплитуда силы равна единице:
Собственная частота колебаний груза на пружине:
Амплитуда при резонансе таких колебаний равна:
🎦 Видео
Вынужденные колебания линейного осциллятора | Общая физика. Механика | Евгений БутиковСкачать

1 Лекция 12 Затухающие и вынужденные колебанияСкачать
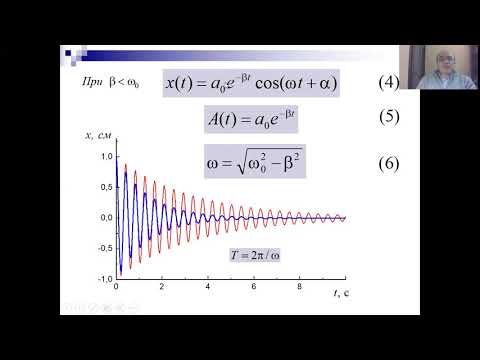
10й класс; Физика; "Затухающие колебания и вынужденные колебания. Резонанс. Применение"Скачать

Дифференциальные уравнения. 11 класс.Скачать

Колебания в электрической цепи и дифференциальные уравненияСкачать

Якута А. А. - Механика - Вынужденные колебания. АЧХ. ФЧХСкачать
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Свободные электромагнитные колебания. 11 класс.Скачать

Урок 361. Вынужденные колебания в последовательном колебательном контуреСкачать

Свободные и вынужденные колебанияСкачать

Урок 343. Затухающие колебания (часть 1)Скачать

Честный вывод уравнения колебанийСкачать

Вынужденные колебания механических систем, Киевнаучфильм, 1974Скачать