Окружность — основная фигура в геометрии, свойства которой рассматривают в школе в 8 классе. Одна из типичных задач, связанных с окружностью, заключается в нахождении площади некоторой ее части, которая носит название кругового сектора. В статье приводятся формулы площади сектора и длины его дуги, а также пример их использования для решения конкретной задачи.
Видео:Площадь сектора и сегмента. 9 класс.Скачать
Понятие об окружности и круге
Перед тем как приводить формулу площади сектора окружности, рассмотрим, что собой представляет указанная фигура. Согласно математическому определению, под окружностью понимают такую фигуру на плоскости, все точки которой равноудалены от некоторой одной точки (центра).
Вам будет интересно: Вячеславна или Вячеславовна? Учимся правильно писать.
Когда рассматривают окружность, то пользуются следующей терминологией:
- Радиус — отрезок, который проводится от центральной точки до кривой окружности. Его принято обозначать буквой R.
- Диаметр — это отрезок, который соединяет две точки окружности, но при этом проходит также через центр фигуры. Его обычно обозначают буквой D.
- Дуга — это часть кривой окружности. Измеряют ее либо в единицах длины, либо с использованием углов.
Круг — еще одна важная фигура геометрии, он представляет собой совокупность точек, которая ограничена кривой окружности.
Видео:Геометрия 9 класс (Урок№24 - Площадь круга. Площадь кругового сектора.)Скачать
Площадь круга и длина окружности
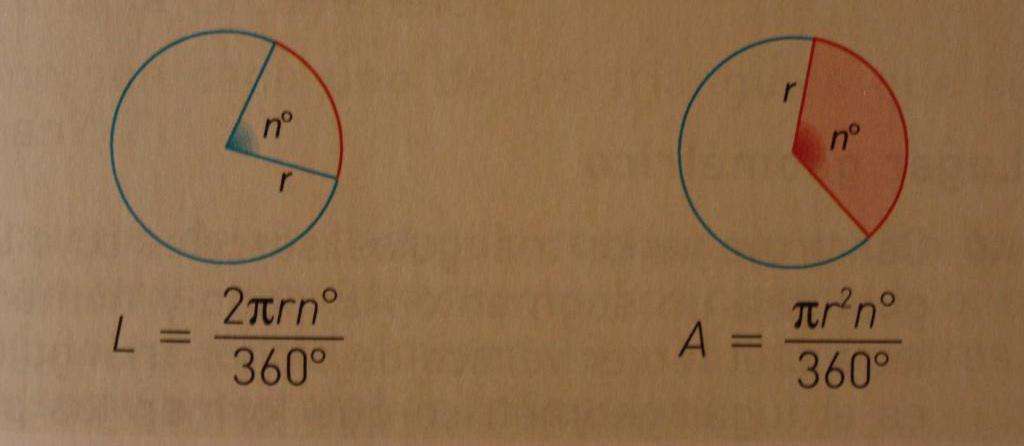
Отмеченные в названии пункта величины рассчитываются с использованием двух простых формул. Они приведены ниже:
- Длина окружности: L = 2*pi*R.
- Площадь круга: S = pi*R2.
В этих формулах pi — это некоторая константа, которая называется числом Пи. Оно является иррациональным, то есть не может быть точно выражено простой дробью. Приблизительно число Пи равно 3,1416.
Как видно из приведенных выражений, чтобы рассчитать площадь и длину достаточно знать только радиус окружности.
Видео:17 задание ОГЭ. 17.1.4. Окружность, круг и их элементыСкачать
Площадь сектора круга и длина его дуги
Перед тем как рассматривать соответствующие формулы, напомним, что угол в геометрии принято выражать двумя основными способами:
- в шестидесятеричных градусах, причем полный оборот вокруг своей оси равен 360o;
- в радианах, которые выражаются в долях числа pi и связаны с градусами следующим равенством: 2*pi = 360o.
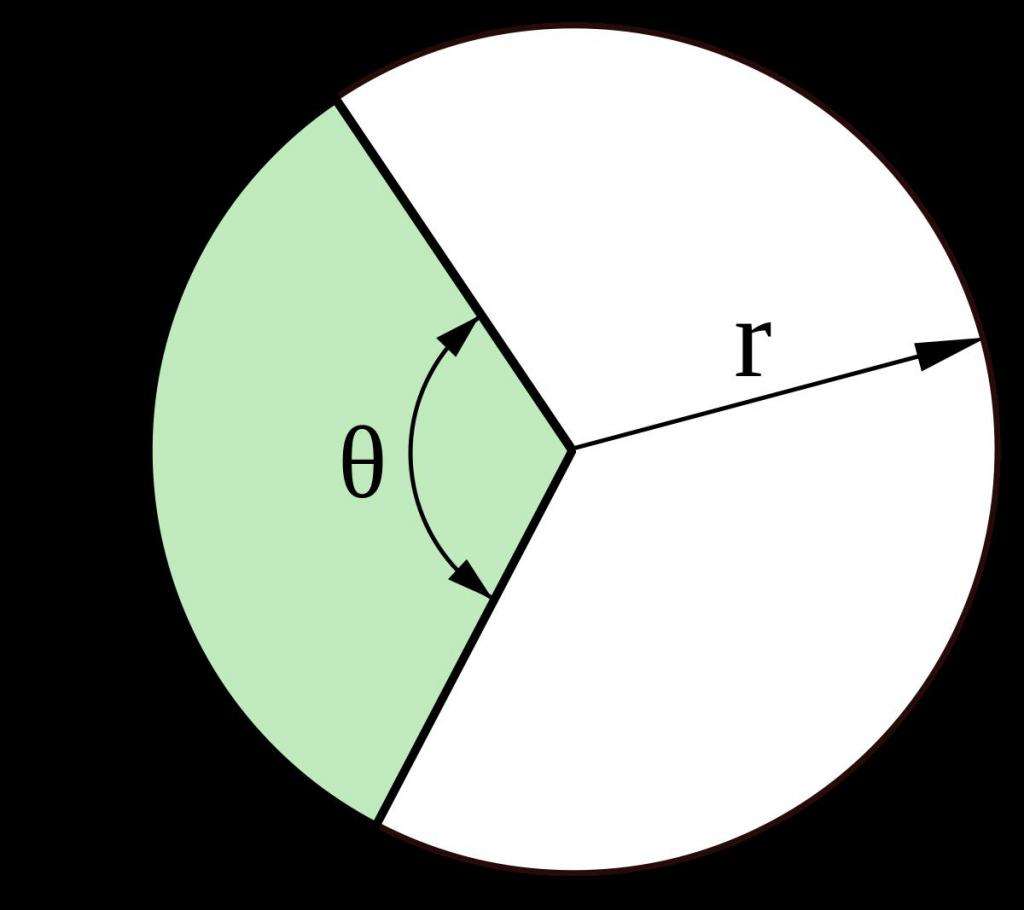
Сектор круга — это фигура, ограниченная тремя линиями: дугой окружности и двумя радиусами, находящимися на концах этой дуги. Пример кругового сектора изображен на фото ниже.
Получив представление о том, что такое сектор для круга, легко понять, как вычислить его площадь и длину соответствующей дуги. Из рисунка выше видно, что дуге сектора соответствует угол θ. Мы знаем, что полная окружность соответствует 2*pi радианам, значит, формула площади кругового сектора примет вид: S1 = S*θ/(2*pi) = pi*R2*θ/(2*pi) = θ*R2/2. Здесь угол θ выражен в радианах. Аналогичная формула площади сектора в случае, если угол θ измеряется в градусах, будет иметь вид: S1 = pi*θ*R2/360.
Длина дуги, образующей сектор, вычисляется по формуле: L1 = θ*2*pi*R/(2*pi) = θ*R. И если θ известен в градусах, тогда: L1 = pi*θ*R/180.
Видео:Урок 13. Геометрия. Углы, связанные с окружностью. Длина дуги. Площадь кругового сектора.Скачать
Пример решения задачи
Покажем на примере простой задачи, как пользоваться формулами площади сектора круга и длины его дуги.
Известно, что колесо имеет 12 спиц. Когда колесо делает один полный оборот, то оно преодолевает расстояние 1,5 метра. Чему равна площадь, заключенная между двумя соседними спицами колеса, и чему равна длина дуги между ними?
Как видно из соответствующих формул, чтобы ими пользоваться, необходимо знать две величины: радиус окружности и угол дуги. Радиус можно вычислить, исходя из знания длины окружности колеса, поскольку пройденное им расстояние за один оборот, точно ей соответствует. Имеем: 2*R*pi = 1,5, откуда: R = 1,5/(2*pi) = 0,2387 метра. Угол между ближайшими спицами можно определить, зная их число. Полагая, что все 12 спиц делят равномерно круг на равные сектора, мы получаем 12 одинаковых секторов. Соответственно, угловая мера дуги между двумя спицами равна: θ = 2*pi/12 = pi/6 = 0,5236 радиан.
Мы нашли все необходимые величины, теперь их можно подставить в формулы и посчитать требуемые условием задачи значения. Получаем: S1 = 0,5236*(0,2387)2/2 = 0,0149 м2, или 149 см2; L1 = 0,5236*0,2387 = 0,125 м, или 12,5 см.
Видео:9 класс, 28 урок, Площадь кругового сектораСкачать
Геометрия. 9 класс
Впишите пропущенное слово.
Вычеркните слово так, чтобы получилось верное утверждение.
Выберите правильный ответ.
Питон длиной 7 м свернулся в круг. Найдите площадь образуемого им круга.
Выберите правильный ответ.
Найдите площадь закрашенного сектора круга, R = 6.
Впишите пропущенное слово.
Выберите правильный ответ.
Выберите правильное уравнение для расчета площади кругового сектора, ограниченного дугой с углом α.
Выберите правильный ответ.
Рассчитайте площадь закрашенного сектора, если r = 8, R = 13, Α = 125°. Ответ округлите до десятых.
Видео:Круговой сектор. 5 класс.Скачать
Способы нахождения площади кругового сектора
Видео:ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать
Определение кругового сектора
Пусть имеется окружность радиусом R. Из центра проведем два радиуса под углом α друг к другу, при этом радиусы будет стягивать дуга длиной L.
Полученная поверхность, ограниченная радиусами окружности и образованной этими радиусами дугой, называется круговым сектором.
Угол α — центральный угол.
Важно знать, что круговой сектор представляет собой развертку боковой поверхности конуса. При этом образующая конуса соответствует радиусу сектора, длина основания конуса — длине дуги сектора.
Видео:Площадь сектораСкачать
Формулы площади кругового сектора
Площадь кругового сектора выражается через центральный угол дуги. Как известно, угол может быть задан в радианной мере или в градусной.
- центральный угол, выраженный в угловых градусах — α;
- длину дуги —L;
- радиус — R.
Тогда выражение для вычисления площади кругового сектора через радиус и длину дуги будет иметь вид:
Из курса геометрии (8-9 классы) известно следующее выражение для нахождения длины дуги сектора круга:
где α р а д — центральный угол, Рад.
Узнаем, как найти площадь сектора через центральный угол, заданный в радианах. Для этого подставим в выражение для L в формулу площади.
S = R · L 2 = R · α р а д · R 2 = α р а д · R 2 2
Теперь переведем угол в радианах в градусы и приведем соответствующую формулу для расчета площади.
S = α р а д · R 2 2 = R 2 · α · π 2 · 180 ° = π α R 2 360 °
Видео:Длина окружности. Площадь круга - математика 6 классСкачать
Примеры решения задач
Вычислить площадь кругового сектора, если его радиус 15 м, а центральный угол равен 2 Рад.
Воспользуемся формулой: S = α р а д · R 2 2
Подставим известные значения и найдем площадь.
S = 2 · 15 2 2 = 225 м 2
Дана окружность с центром O и радиусом 10 см. Через окружность проведена хорда MN так, что в результате получился правильный треугольник MON. Найти площадь заштрихованной фигуры.
Искомую площадь будем искать как разность площади сектора, заданного радиусами и дугой MN, и площади треугольника MON. Поскольку треугольник правильный, все его стороны равны радиусу, а каждый из углов равен 60 ° .
Узнаем, чему равна площадь кругового сектора. Для этого воспользуемся формулой для угла в градусной мере.
S с е к т о р а = παR 2 360 ° = 3 . 14 · 60 ° · 10 2 360 ° = 52 . 3 с м 2
Теперь найдем площадь треугольника MON.
S M O N = O M 2 · 3 4 = R 2 · 3 4 = 100 · 3 4 = 43 . 3 с м 2
Найдем площадь искомой поверхности
S = S с е к т о р а — S M O N = 52 . 3 — 43 . 3 = 9 с м 2
Известен радиус кругового сектора R и длина его дуги L. Определить, чему равна высота конуса, полученного из заданного сектора.
Круговой сектор есть развертка боковой поверхности конуса. Сделаем рисунок, на котором покажем конус в продольном разрезе. Получим равнобедренный треугольник. Обозначим его MNK, а высоту — NH.
Высоту MH найдем как катет прямоугольного треугольника MNH. Образующая конуса MN равна радиусу кругового сектора, то есть MN=NK=R. Сторона MH равна радиусу основания конуса — R_. Радиус основания вычислим через длину.
L к о н у с а = 2 π R к о н у с а ⇒ R к о н у с а = L к о н у с а 2 π
Н о L к о н у с а = L , т о г д а R к о н у с а = L 2 π .
Теперь по теореме Пифагора вычислим NH.
N H = M N 2 — N H 2 = R 2 — R к о н у с а 2 = R 2 — L 2 π 2
🔍 Видео
Площадь круга. Математика 6 класс.Скачать
ГЕОМЕТРИЯ 9 класс: Длина окружности, площадь круга и площадь кругового сектораСкачать
Длина окружности. Площадь круга. 6 класс.Скачать
Геометрия 9 класс (Урок№23 - Длина окружности.)Скачать
Площадь круга. 9 класс.Скачать
Длина окружности и площадь круга. Урок 12. Геометрия 9 классСкачать
ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать
Длина окружности. Площадь круга 9 классСкачать
Лучший способ найти площадь кругаСкачать
Длина окружности. 9 класс.Скачать
Длина окружности. Математика 6 класс.Скачать
