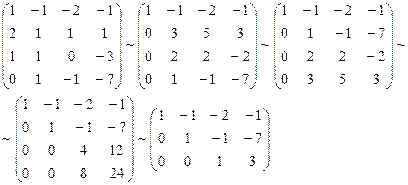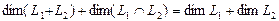Все векторы из rn координаты которых удовлетворяют уравнению (5 видео)

Содержание

Линейные оболочки и подпространства
5.1.6. Примеры решения задач по теме «Линейные операторы и квадратичные формы»
Задачи и упражнения для самостоятельной работы
💥 Видео

Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Линейные оболочки и подпространства

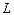
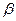
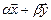
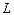
Определение. Подпространством линейного пространства называется множество векторов из такое, что для любых двух векторови из и любых двух вещественных чисел и линейная комбинация также принадлежит .

Утверждение. Подпространство само является линейным пространством.

Определение. Линейной оболочкой системы векторов называется множество всех линейных комбинаций векторов . Обозначается .

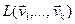
Утверждение. Линейная оболочка системы векторов является подпространством.

Определение. Пересечением двух подпространств и называется множество всех векторов, принадлежащих одновременно и ,и . Обозначается .

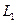
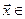
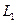
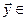
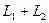
Определение. Суммой двух подпространств и называется множество всех векторов , представимых в виде , где , . Обозначается .

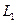
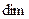
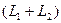
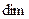
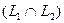
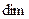
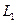
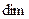
Утверждение. Сумма и пересечение подпространств и являются линейными пространствами, и их размерности связаны равенством

+ = + .

Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.

Примеры

1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами .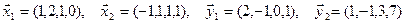

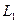
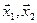
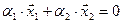
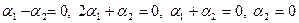
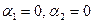
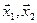
Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства , порождённого векторами , равенство нулю линейной комбинации , эквивалентное системе уравнений , достигается лишь при условии . Следовательно, векторы линейно

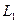
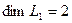
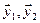
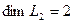
независимы и размерность подпространства равна 2: . Для подпространства , порождённого векторами , проводя аналогичный анализ, получим .

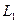
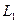
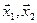
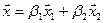
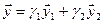
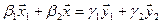
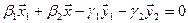
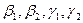
Вычислим теперь размерность пересечения подпространств и . По определению векторы, составляющие пересечение, принадлежат одновременно обоим подпространствам. Произвольный вектор подпространства является линейной комбинацией базисных векторов : . Аналогично для подпространства имеем , тогда условие принадлежности пересечению есть или .

Это условие представляет собой систему уравнений относительно коэффициентов . Составим матрицу системы и упростим её с помощью элементарных преобразований:

Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим ,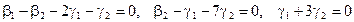

откуда .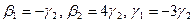

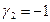
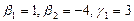
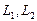
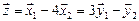
Полагая свободное неизвестное , для остальных имеем

. Итак, пересечение подпространств имеет один базисный вектор

Размерность пересечения 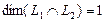. Следовательно, в соответствии с равенством

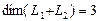
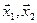
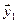
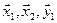
размерность суммы подпространств . В качестве базиса суммы подпространств можно взять, например, векторы , дополненные вектором . В линейной независимости векторов убедиться нетрудно.

Задачи

3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами , , , , .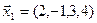

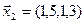
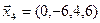
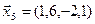
3.40. Найти размерность и какой-либо базис линейной оболочки векторов , , , , .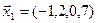

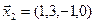
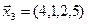
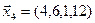
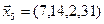
3.41. Является ли подпространством в указанном пространстве множество

а) векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R 2 ;

б) бесконечно малых числовых последовательностей в пространстве сходящихся последовательностей;

в) сходящихся к числу последовательностей в пространстве сходящихся последовательностей;

г) диагональных матриц в пространстве квадратных матриц того же порядка;

д) невырожденных матриц в пространстве симметричных матриц того же порядка;

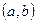
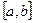
е) дифференцируемых на интервале функций в пространстве функций, непрерывных на отрезке .

3.42. Почему не является подпространством в указанном пространстве множество

а) векторов, каждый из которых лежит на одной из координатных плоскостей, в пространстве R 3 ;

б) векторов из пространства R n , координаты которых удовлетворяют уравнению ;

в) расходящихся числовых последовательностей в пространстве ограниченных последовательностей;

г) вырожденных матриц в пространстве квадратных матриц того же порядка;

д) монотонно возрастающих и ограниченных на множестве 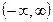функций в пространстве функций, ограниченных на том же множестве.

3.43. Найти размерность и какой-либо базис подпространства решений однородной системы:

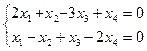
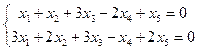
а) ; б) ;

в) .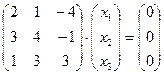

3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:

а) все n-мерные векторы, координаты которых удовлетворяют уравнению ;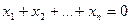

б) все n-мерные векторы, у которых первая координата равна нулю;

в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;

г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;

д) все n-мерные векторы, у которых координаты с нечетными номерами равны между собой.

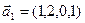
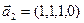
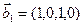
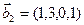
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами , и , . Является ли эта сумма прямой суммой?

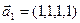
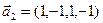
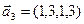
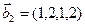
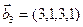
3.46. Найти размерность суммы и пересечения линейных оболочек векторов , , и , , . Является ли их cумма прямой?

3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами и , если

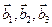
а) , , , , , ;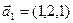

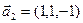
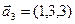
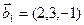
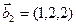
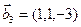
б) , , , , , .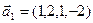

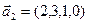
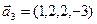
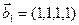
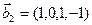
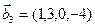
3.48. Найти базис суммы и пересечения линейных оболочек и , если

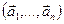
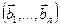
а) , , , ;

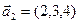
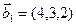
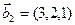
б) , , , , , .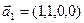

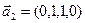
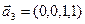
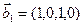
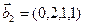
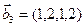
Является ли прямой сумма этих подпространств?

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

5.1.6. Примеры решения задач по теме «Линейные операторы и квадратичные формы»

Пусть Е1, Е2, Е3, Е4 – базис в векторном пространстве. Разложить вектор

Выпишите матрицу перехода от старого базиса к новому, столбцами которой являются координаты новых базисных векторов в старом базисе. Строки этой матрицы являются коэффициентами в формулах преобразования старых координат через новые.

Выпишем матрицу перехода от старого базиса к новому, столбцами которой являются координаты новых базисных векторов в старом базисе:

Строки этой матрицы являются коэффициентами в формулах преобразования старых координат через новые.

Координаты вектора Х в старом базисе: Х = (1; 2; -1; 3). Пусть в новом базисе он имеет координаты: X = (X, Y, Z, T). Тогда, используя матрицу Т, найдем связь между старыми и новыми координатами:

Следовательно, в новом базисе Х = (-1; 3; -4; 3).

Найти матрицу А’ оператора А:

Искомая матрица А’ = T-1 A T, где Т – матрица перехода из старого базиса к новому.

Искомая матрица А’ = T-1 A T, где Т – матрица перехода из старого базиса к новому. Составим матрицу Т :

Ответ: .

Найти собственные числа и собственные векторы линейного оператора, заданного матрицей

Для определения собственных чисел составьте характеристическое уравнение:

Координаты собственных векторов RI = (Xi, Yi) должны удовлетворять системе уравнений, коэффициенты которых получены из элементов строк определителя, стоящего в левой части характеристического уравнения, при подстановке LI.

Составим характеристическое уравнение:

Найдем собственные векторы:

1) для L = -2 координаты собственного вектора R1 = (X1, Y1) должны удовлетворять системе уравнений, коэффициенты которых получены из элементов строк определителя, стоящего в левой части характеристического уравнения, при подстановке L = -2:

Если Х1 = 1, то У1 = -1, и R1= (1; -1). Остальные собственные векторы коллинеарны вектору (1; -1), и общий вид собственного вектора, соответствующего L = -2: R1 = С1(1; -1), где С1 – произвольная постоянная.

2) для L = 6 координаты собственного вектора R2 (X2; Y2) удовлетворяют системе:

Пусть Х2 = 3, тогда У2 = 5, и R2 = (3; 5). Соответственно общий вид второго собственного вектора: R2 = С2(3; 5).

Ответ: собственные числа L1 = -2, L2 = 6; собственные векторы R1 = С1(1; -1),

В пространстве 3-мерных векторов задан оператор

Где I – базисный вектор декартовой системы координат.

Выяснить геометрический смысл этого оператора.

Множитель Xi – скалярное произведение, то есть число, поэтому вектор (Xi)I коллинеарен оси Ох.

Оператор А переводит произвольно направленный вектор Х в вектор

KI, коллинеарный оси Ох, поскольку первый множитель – скалярное произведение, то есть число. Из определения скалярного произведения следует, что

Следовательно, А – оператор проектирования на ось Ох.

Оператор осуществляет проектирование вектора Х на ось Ох;

Привести матрицу А линейного оператора к диагональному виду и найти соответствующий базис, если

Найдите собственные числа и собственные векторы матрицы линейного оператора, задайте базис из линейно независимых собственных векторов R1, R2, R3 , в котором матрица оператора примет диагональный вид, и составьте матрицу перехода к новому базису.

Найдем собственные векторы, соответствующие полученным собственным числам.

Подставим в строки определителя L = 2 и найдем связь между координатами собственного вектора R2 = (X2, Y2, Z2):

Та же зависимость получается для координат третьего собственного вектора R3 = (X3, Y3, Z3). Выберем значения двух координат каждого из этих векторов так, чтобы R2 и R3 были линейно независимы.

Пусть Х2 = 1, У2 = 0, тогда Z2 = -3, и R2 = (1; 0; -3).

Получен базис из линейно независимых собственных векторов R1, R2, R3 , в котором матрица оператора примет диагональный вид.

Составим матрицу перехода к новому базису:

Найдем матрицу, обратную к Т:

Тогда в базисе из собственных векторов матрица оператора

Ответ: в базисе (1; 1; 1), (1; 0; -3), (0; 1; 3) матрица оператора

Линейный оператор А задан в некотором базисе матрицей

Найти собственные числа и собственные векторы оператора А-1 – оператора, обратного к А.

Собственные числа обратного оператора являются обратными к собственным числам данного оператора, а их собственные векторы одинаковы.

Характеристическое уравнение для А:

Найдем матрицу обратного оператора:

Соответствующее характеристическое уравнение:

Составить матрицу квадратичной формы 3Х2 – 10Ху + 8У2 и найти ее собственные числа.

Матрица квадратичной формы А11Х2 + 2А12Ху + А22У2 является

Симметрической (Aij = Aji) и имеет вид:

В нашей задаче А11 = 3, А12 = -5, А22 = 8. Следовательно,

Составим характеристическое уравнение, корнями которого являются собственные числа:

Ответ: матрица квадратичной формы ,

Собственные числа

Найти базис, в котором квадратичная форма 2Х2 + 4Ху + 5У2 будет иметь канонический вид, и указать этот вид.

Канонический вид квадратичной формы:

1) во-первых, не содержит произведения Ху;

2) во-вторых, коэффициенты при Х2 и У2 равны собственным числам матрицы квадратичной формы.

Базис, в котором квадратичная форма имеет канонический вид, состоит из нормированных собственных векторов матрицы квадратичной формы.

Матрица квадратичной формы

Собственные числа: L1 = 1, L2 = 6.

Для L1 = 1 координаты вектора R1 = <X1, Y1> определяются уравнением

Х1 + 2У1 = 0, Х1 = -2У1. Если У1 = 1, то Х1 = -2, и R1 = C. Найдем значение С из условия, что вектор R1 нормирован, то есть его длина равна 1:

Итак, базис имеет вид:

И в этом базисе квадратичная форма примет вид: L1Х2 + L2У2, то есть Х2 + 6У2.

Ответ: в базисе квадратичная форма имеет канонический вид: Х2 + 6У2.

Указать преобразование координат, приводящее квадратичную форму

8Х2 – 12Ху + 17У2 к каноническому виду.

Матрица преобразования координат имеет вид:

Где R1 = (X1, Y1) и R2 = (X2, Y2) – нормированные собственные векторы.

Найдем базис из нормированных собственных векторов.

Составим матрицу перехода к новому базису, столбцами которой будут координаты новых базисных векторов R1, R2 в старом базисе:

Строки этой матрицы определяют коэффициенты уравнений, выражающих старые координаты через новые:

Где Х, У – координаты в старом базисе, а Х’, Y’ – в новом.

Таким образом, найдено искомое преобразование.

Ответ: .

Привести к каноническому виду квадратичную форму 5Х2 – 12Ху.

Матрица преобразования координат имеет вид:

Где R1 = (X1, Y1) и R2 = (X2, Y2) – нормированные собственные векторы. В новом базисе квадратичная форма имеет канонический вид, причем коэффициенты при Х2 и У2 совпадают с собственными числами матрицы квадратичной формы.

Матрица перехода к базису из собственных векторов:

Подставим найденные выражения в квадратичную форму:

Как и следовало ожидать, в новом базисе квадратичная форма имеет канонический вид, причем коэффициенты при Х2 и У2 совпадают с собственными числами матрицы квадратичной формы.

Найти преобразование координат, приводящее квадратичную форму

X2 + Y2 + 5Z2 – 6Xy + 2Xz – 2Yz к каноническому виду.

Матрица преобразования координат:

Для заданной квадратичной формы

Составим и решим характеристическое уравнение:

(Мы не останавливаемся подробно на способах решения уравнений высших порядков. В данном случае, например, один из корней был найден перебором делителей свободного члена, а затем левая часть разложена на множители.)

Найдем нормированные собственные векторы:

Матрица перехода к новому базису:

Задает преобразование координат:

Заметим, что в новых координатах квадратичная форма примет вид:

Где коэффициенты являются собственными числами, стоящими в той же последовательности, что и соответствующие собственные векторы в матрице Т.

Ответ:

Видео:Координаты вектора. 9 класс.Скачать

Задачи и упражнения для самостоятельной работы

Нет. Например, для многочленов 3 ей степени

и сумма будет многочленом 2 ой степени

3. Образует ли множество радиус-векторов на плоскости, концы которых находятся в первой четверти, линейное пространство (с обычными операциями)?

Нет. Например, умножение элемента данного множества на 3 равен 0? Да.

5. Образуют ли линейное пространство все полиномы от х степени не выше 5, у которых коэффициент при х 3 равен 1? Нет.

18. Разложить матрицы в сумму симметрической S и кососимметрической А:
- а) ; б) ; в) .

19. Найти:
- а) ; б) .

20. Найти произведение матриц:
- а) ; б) .

21. Найти произведение матриц:
- а) ; б) ; в) ;

г) ;
д) .

22. Вычислить произведение матриц:
- а) ; б) ;

23. Вычислить произведения матриц:
- а) ; б) ;

в) ;
г) .

24. Пусть ; ; . Проверить, что . .

25. Даны матрицы:;

26. Для заданных пар матриц проверить выполняется ли равенство: :
- а) ; б) ; в)

. а) да; б) нет; в) нет.

27. Показать, что для матрицы А: :

28. Если , то . Вычислить , если:

б) ; ;
в) ; ;
г) ; .

29. Проверить, что для матриц Паули: , . Справедливы следующие соотношения:

а) ;
б) ;

30. Показать, что все матрицы перестановочные с матрицей: имеют вид: , где — произвольные числа.
31. Найти все матрицы перестановочные с матрицей:
- а) ; б) ; в) .

32. Для матриц и найти: а) ; б) .

33. Выяснить, образует ли данное линейное множество функций на произвольном отрезке [a, b] линейное пространство относительно обычных операций сложения и умножения на число:
- а) множество С_{[a, b]} функций непрерывных на [a, b];
- б) множество С 1 _{[a, b]} функций непрерывно дифференцируемых на [a, b];
- в) множество R_{[a, b]} функций интегрируемых по Риману на [a, b];
- г) множество функций, ограниченных на [a, b];

д) множество функций таких, что ;
е) множество функций неотрицательных на [a, b];
ж) множество функций таких, что ;
з) множество функций таких, что ;

и) множество функций таких, что ;
к) множество функций, монотонно возрастающих на [a, b];
л) множество функций, монотонных на [a, b].

а) да; б) да; в) да; г) да; д) нет; е) нет; ж) да; з) нет; и) нет; к) нет; л) нет.

34. Выяснить, является ли подпространством данное множество векторов в n-мерном арифметическом пространстве и если является, то найти его размерность:
- а) множество векторов, у которых первая координата равна 0;
- б) множество векторов, у которых все координаты равны между

в) множество векторов сумма координат которых равна 0;
г) множество векторов сумма координат которых равна 1;
д) множество векторов плоскости параллельных данной прямой;
е) множество векторов трехмерного пространства, перпендикулярных

ж) множество векторов плоскости с модулем, не превышающем

з) множество векторов плоскости, образующих угол с данной

а) да, n -1; б) да, 1; в) да, n-1; г) нет; д) да, 1; е) да, 2; ж) нет; з) при = 0 и = /2 — да, 1;

35. Является ли линейным подпространством соответствующего линейного пространства каждая из соответствующих совокупностей векторов:
- а) все векторы n-мерного пространства с целыми координатами;
- б) все векторы плоскости, каждый из которых лежит на одной из осей

координат Ох или Оу;

в) все векторы начала и концы которых лежат на данной прямой;
г) все векторы трехмерного пространства, концы которых не лежат на

а) нет; б) нет; в) да; г) нет.

36. Доказать, что следующие системы векторов образуют линейные подпространства, и найти их базис и размерность:
- а) все n-мерные векторы, у которых первая и последняя координаты

равны между собой;

б) все n-мерные векторы у которых координаты с четными номерами

в) все n-мерные векторы, у которых координаты с четными номерами

равны между собой;

г) все n-мерные векторы вида , где и — лю-

а) n-1; (1, 0, … , 0, 1), (0, 1, 0, … , 0), (0, 0, 1, 0, … , 0), (0, 0, … , 0, 1, 0); б) [(n+1)/2];

(1, 0, 0, , … , 0), (0, 0, 1, 0, … , 0), (0, 0, 0, 0, 1, 0, … , 0)…; в) [(n+1)/2]+1; (0, 1, 0, 1, 0,1, …),
(1, 0, 0, … , 0), (0, 0, 1, 0, … , 0), (0, 0, 0, 0, 1, 0,… , 0)…; г) 2; (1, 0, 1, 0, 1, … ),
(0, 1, 0, 1, 0, 1, 0, … ).
37. Выяснить, является ли данное множество квадратных матриц порядка n линейным подпространством в пространстве всех квадратных матриц порядка n и, если является, то найти его размерность:
- а) множество матриц с нулевой первой строкой;
- б) множество диагональных матриц;
- в) множество верхних треугольных матриц;
- г) множество симметрических матриц;
- д) множество кососимметрических матриц.

38. Установить, являются ли следующие совокупности векторов подпространствами:
- а) совокупность всех векторов n-мерного пространства (n 2), у которых, по крайней мере, одна из первых двух координат равна нулю;
- б) совокупность всех векторов n-мерного пространства, у которых первые две координаты и удовлетворяют уравнению: ;
- в) совокупность всех векторов n-мерного пространства, у которых первые две координаты удовлетворяют уравнению: ;
- г) все векторы плоскости, концы которых лежать на одной прямой, а начало совпадает с началом координат;
- д) все векторы, являющиеся линейными комбинациями данных векторов из .

а) нет; б) да; в) нет; г) да, если прямая проходит через начало координат; нет, если прямая не проходит через начало координат; д) да.

39. В пространстве полиномов степени не выше 3 является ли подпространством совокупность полиномов, удовлетворяющих условию:
- а) ; б) .

Если да, то какова его размерность и базис?

а) да; 3; Базис: 1, (х 2 -1), (х 2 -1) х; б) да; 3; Базис: х, х 2 +1, х 3 +2

40. В пространстве полиномов степени не выше 3, найти базис и размерность подпространства L полиномов, удовлетворяющих условиям:
- а) ; б) ;
- в) ; г) ; д) .

a) dim L = 2; ; б) dim L = 2; ;

в) dim L = 2; ; г) dim L = 3; ;

д) dim L = 3; .
41. В пространстве полиномов степени не выше трех является ли подпространством совокупность полиномов, таких, что . Найти базис и размерность этого пространства.

42. Доказать, что при любом данное множество функций образует конечномерное линейное пространство, найти размерность и указать базис этого пространства:
- а) множество четных полиномов, степени не выше n;
- б) множество нечетных полиномов, степени не выше n;
- в) множество тригонометрических полиномов порядка не выше n, т.е.

множество функций вида:

г) множество четных тригонометрических полиномов порядка не выше n;
д) множество нечетных тригонометрических полиномов порядка не выше n;
е) множество функций вида:

где — фиксированное вещественное число.

базис: 1, cosx, sinx, … , cosnx, sinnx; г) n+1; базис: 1, cosx, … , cosnx; д) n; базис:

43. Доказать, что данное множество функций образует бесконечномерное линейное пространство:
- а) множество всех полиномов;
- б) множество всех тригонометрических полиномов;
- в) множество функций непрерывных на некотором отрезке.
44. Выяснить, будут ли данные векторы линейно зависимы или нет:
- а) а(1, 3, 1), b(-1, 1, 3), c(-5, -7, 3);
- б) а(2, -1, -2), b(6, -3, 1);
- в) а(2, -1, 7, 3), b(1, 4, 11, -2), c(3, -6, 3, 8).

а) да; 2а —b = 0; б) нет; в) да; 3а — b = 0; г) нет; д) да; а + b + с = 0; е) нет.

47. Найти размерность и базис линейных подпространств натянутых на системы векторов:
- а) а₁(1, 0, 0, -1), а₂(2, 1, 1, 0), а₃(1, 1, 1, 1), а₄(1, 2, 3, 4), а₅(0, 1, 2, 3);
- б) а₁(1, 1, 1, 1, 0), а₂(1, -1, -1, -1, -1), а₃(2, 2, 0, 0, -1), а₄(1, 1, 5, 5, 2),

а) нет; б) да; в) нет; г) да; д) да; е) нет.

49. Какова размерность пространства решений уравнения:
- а) ; б)

50. Докажите, что следующие системы функций линейно независимы
а) sinx, sin2x, sin3x; б) 1, e x , e 2x , e 3x .
51. Пусть R + линейное пространство положительных чисел, в котором х ? у ? х . у, а ? х ? х. Доказать, что в R + любые х и у линейно зависимы.
52. Выявить линейные зависимости между векторами:
- а) (1, 3), (3, 2), (-11, 16);
- б) (1, 1, 1, 1),(1, 1, 1, 3), (3,-5, 7, 2), (1,-7, 5,-2);
- в) (4, 3, 1), (1, 2, 3), (2, -1, -5);
- г) (1, 1, 1, 1), (1, 1, 2, 2), (0, 0, 1, 1), (2, 2, 3, 3).

53. Векторы e1, e2, … , en в X заданы своими координатами в некотором базисе. Показать, что e1, e2, … , en сами образуют базис и найти координаты вектора х в этом базисе:
- а) e₁(1, 1, 1), e₂(1, 1, 2), e₃(1, 2, 3), x = (6, 9, 14);
- б) e₁(2, 1, -3), e₂(3, 2, -5), e₃(1, -1, 1), x = (6, 2, -7);
- в) e₁(1, 2,-1,-2), e₂(2, 3, 0, -1), e₃(1, 2, 1, 4), e₃(1, 3, -1, 0), x=(7, 14, -1, 2);

а) (1, 2, 3); б) (1, 1, 1); в) (0, 2, 1, 2).

54. Найти координаты вектора х в базисе e1, e2, e3: e1(1. 3. 5), e2(6, 3, 2), e3(3, 1, 0), если:
- а) х(3, 7, 1); б) х(0, 0, 1); в) х(2, 3, 5).

а) (33, -82, 154); б) (-3, 8, -15); в) (-1, 5, -9).

55. Найти координаты функции в базисе .
56. Линейное пространство полиномов степени не выше n. Показать, что 1, (х-1), (х-1) 2 , … , ), (х-1) n образуют базис этого пространства. Найти в этом базисе координаты многочлена:
- а) 2 + 3х — 5х 2 + 4х 5 ; б) а₀ + а₁х + … + а_nхn ;

а) (4, 13, 35, 40, 20, 4, 0, 0, …); б) .

57. Найти размерность и базис линейной оболочки системы полиномов: (1 + t)3, t3, 1, t + t2.

3; базис: (1 + t) 3 , t 3 , 1.

58. Доказать, что матрицы образуют базис в пространстве квадратных матриц 2го порядка и найти координаты матрицы в этом базисе.

59. Доказать, что многочлены 2t + t5, t3 — t5, t + t3 образуют базис в пространстве нечетных полиномов степени не выще 5 и найти координаты полинома 5t — t3 + 2t5 в этом базисе.

60. Проверить, что матрицы образуют базис в пространстве квадратных матриц 2го порядка. Матрицу представить, как линейную комбинацию базисных матриц.

61. Доказать, что пространство квадратных матриц порядка n является прямой суммой подпространства симметрических матриц и подпространства кососимметрических матриц того же порядка.
62. Доказать, что пространство многочленов степени не выше n является прямой суммой четных многочленов степени не выше n и подпространства нечетных многочленов степени не выше n.
63. Доказать, что n-мерное линейное пространство является прямой суммой подпространства векторов. Все координаты которых равны между собой и подпространства векторов сумма координат которых равна нулю.
64. Доказать, что сумма L двух подпространств P и Q тогда и только тогда будет прямой суммой, когда хотя бы один вектор хL однозначно представляется в виде х = y + z, где уP, zQ.
65. Пусть P и Q два линейных подпространства конечномерного линейного пространства V. Доказать, что:
- а) dim P + dim Q >n = dim VxV, x , xPQ;
- б) dim P + dim Q = dim PQ + 1, то одно из этих подпространств

содержится в другом.

66. Доказать, что для любого линейного подпространства P конечномерного линейного пространства V, существует другое подпространство Q такое, что V = PQ.
67. Найти размерность суммы и размерность пересечения линейных подпространств натянутых на системы векторов <a_i> и <b_i>:
- а) а₁(1, 2, 0, 1), а₂(1, 1, 1, 0); b₁(1, 0, 1, 0), b₂(1, 1, 1, 1);
- б) а₁(1, 1, 1, 1), а₂(1, -1, 1, -1), а₃(1, 3, 1, 3); b₁(1, 2, 0, 2), b₂(1, 2, 1, 2),

69. Найти размерность и базис суммы и пересечения линейных подпространств пространства многочленов степени не выше 3, натянутых на системы многочленов:
1 + 2t + t 3 , 1 + t + t 2 , t — t 2 + t 3 и 1 + t 2 , 1 + 3t + t 3 , 3t — t 2 + t 3 .

сумма: 3; базис: <1 + 2t + t 3 , 1 + t 2 , 1 + t + t 2 >; пересечение: 1; базис: <2 + 3t + t 2 + t 3 >.

70. а) Доказать, что если в n-мерном комплексном линейном пространстве рассматривать умножение векторов лишь на вещественные числа, то получим 2n-мерное вещественное пространство;
б) В двумерном комплексном арифметическом пространстве рассматривается операция умножения лишь на вещественные числа. Найти базис в полученном вещественном пространстве и координаты вектора (-3 + 2i, —i) в этом базисе.

71. Найти размерность и базис суммы и пересечения линейных подпространств комплексного n-мерного арифметического пространства, натянутых, на системы векторов и :
- а) n = 3; а₁(1, 2, 3), а₂(1, -2, i), а₃(2, 0, 3 + i); b₁(1, 0, 3i), b₂(1, 4, 3 + i),

в) 4; базис: а₁, а₂, а₂, b₄; 2; базис: b₁, b₂ .
72. Доказать, что множество многочленов степени не выше n с комплексными коэффициентами можно рассматривать и как комплексное линейное пространство и как вещественное линейное пространство. В обоих случаях найти:
- а) базис и размерность;

б) координаты многочлена в найденном базисе
(при n = 2).

a) Комплексное пространство: dim V = n+1, базис: 1, t, t 2 , … t n ; Вещественное пространство:

Вещественное пространство: (1, -2, 3, 1, -3, 0).

73. Для заданных матриц А и В найти А+ .В, если:
- а) ;

б);
в) ;
г) ;
д) ;
е) .

е) .
74. Произвести действия с матрицами:
- а) ;

б) ;
в) ;
г) ;
д).

д) .
75. Квадратная матрица с комплексными элементами называется эрмитовой, если ; и называется унитарной, если .

Квадратная матрица с вещественными элементами называется самосопряженной, если ; и называется ортогональной, если .

Для следующих матриц установить какими из указанных выше характеристик они обладают:

в) ; г) ;
д) ; е) ;

a) ортогональная; б) ортогональна и самосопряженная; в) самосопряженная; г) эрмитова;

д) эрмитова; е) ортогональная; ж) ортогональная; з) ортогональная.
76. Найдите n для указанных ниже пространств, если известно, что эти пространства изоморфны пространству V6:
- а) для пространства симметричных nхn — матриц с нулевыми диагональными элементами;
- б) для пространства Р_n полиномов степени не выше n;
- в) для подпространства многочленов р(х) из Р_n, удовлетворяющих условию: р(0) = 0. a) n = 4; б) n = 5; в) n = 6.