Вириальное уравнение состояния реальных газов (7 видео)

Вириальное уравнение состояния реальных газов

Поведение реального газа можно описать с высокой точностью с помощью вириального уравнения (или уравнения с вириальными коэффициентами). Идея состоит в отказе от минимального числа параметров и использовании бесконечных рядов — разложений по степеням 1/V:

. (1.15)

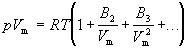
Коэффициенты B₂, B₃, . (которые зависят от температуры и природы рассматриваемого газа, но не зависят от плотности и давления) называются соответственно вторым, третьим, . вириальными коэффициентами. Первый вириальный коэффициент равен 1. Второй вириальный коэффициент обычно более важен, чем последующие, поскольку для большинства случаев B₂ /V_m >> B₃ /V 2 _m >> . .

Уравнение состояния в виде бесконечного ряда (1.15) было предложено Тиссеном в 1885 г. Однако основное развитие вириальное уравнение получило в 1901 г. в работе Камерлинг-Оннеса, который рассмотрел несколько вариантов этого уравнения и предложил называть его коэффициенты вириальными.

Если подходить в вириальному уравнению только как к эмпирическому уравнению состояния, то оно имеет ряд недостатков. Например, как показывают экспериментальные данные, сходимость ряда не очень хорошая, особенно в области высокой плотности. Кроме того, при высоких плотностях для удовлетворительного описания экспериментальных данных необходимо использовать большое число членов ряда, а для этого нужно экспериментально определять большое число вириальных коэффициентов. Более того, часто тот же набор экспериментальных данных можно более точно описать с помощью других эмпирических уравнений с меньшим числом параметров. Однако исключительная важность вириального уравнения состояния заключается в том, что это единственное из известных уравнений состояния, имеющее строгую теоретическую основу. Как будет показано в главе 2, каждый вириальный коэффициент можно выразить через силы межмолекулярного взаимодействия. Так, второй вириальный коэффициент отражает парные взаимодействия, третий – тройные и т.д. Таким образом, вириальное уравнение состояния позволяет объяснить свойства газа с позиции межмолекулярных взаимодействий.

Для некоторых целей вириальное уравнение удобнее записать в виде разложения по степеням p:

Таким образом, вириальное уравнение является примером того, когда простое выражение (в данном случае pV_m = RT) представляет собой только первый член ряда разложения по степеням переменной (в данном случае p или V_m).

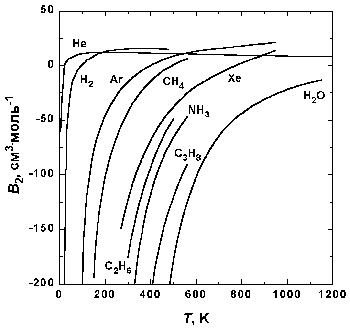
Рис.1.5. Зависимость второго вириального коэффициента некоторых газов от температуры.

На рис. 1.5 представлена зависимость второго вириального коэффициента от температуры для некоторых газов. При низких температурах B₂ n-1 . Таким образом, уравнение Ван-дер-Ваальса качественно правильно передает температурную зависимость второго вириального коэффициента при низких температурах (при низких температурах B₂

[предыдущий раздел]

[содержание]

[следующий раздел]

Вириальное уравнение состояния реальных газов

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Содержание

Вириальное уравнение состояния реальных газов
Вириальные коэффициенты.
Вириальные коэффициенты.
📸 Видео

Видео:Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Вириальное уравнение состояния реальных газов

Вириальное уравнение состояния.

Поведение реального газа можно описать с высокой точностью с помощью вириального уравнения (или уравнения с вириальными коэффициентами). Идея состоит в отказе от минимального числа параметров и использовании бесконечных рядов — разложений по степеням 1/V:

Коэффициенты B2, B3, . (которые зависят от температуры и природы рассматриваемого газа, но не зависят от плотности и давления) называются соответственно вторым, третьим, .вириальными коэффициентами. Первый вириальный коэффициент равен 1. Второй вириальный коэффициент обычно более важен, чем последующие, поскольку для большинства случаев B2 /Vm >> B3 /V2m >> . .

Уравнение состояния в виде бесконечного ряда было предложено Тиссеном в 1885 г. Однако основное развитие вириальное уравнение получило в 1901 г. в работе Камерлинг-Оннеса, который рассмотрел несколько вариантов этого уравнения и предложил называть его коэффициенты вириальными.

Для некоторых целей вириальное уравнение удобнее записать в виде разложения по степеням p: pVm = RT (1 + B2’p + B3’p2 + .)

Таким образом, вириальное уравнение является примером того, когда простое выражение (в данном случае pVm = RT) представляет собой только первый член ряда разложения по степеням переменной (в данном случае p или Vm).

Рис.1.5. Зависимость второго вириального коэффициента некоторых газов от температуры.

На рис. 1.5 представлена зависимость второго вириального коэффициента от температуры для некоторых газов. При низких температурах B2

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Вириальные коэффициенты.

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Вириальные коэффициенты.

Вириальные коэффициенты. Сначала мы ограничиваемся изучением чистых газов, а затем переходим к смешанным газам. Высокоточное давление газа можно представить в виде ряда порядка 1 / v (а молярный объем равен V / p： Где B, C-только функция температуры. Количество терминов, необходимых для описания точек экспериментальных данных в пределах точности измерений, варьируется от 2 до 4 в зависимости от рассматриваемого интервала температур и давлений. Коэффициент/?, Таких как C, 2й, 3й и т. д., называется коэффициентом вириала.

nWrf ВР Во-вторых, коэффициент virpal имеет размерность объема на 1 моль. А в качестве единицы измерения объема часто выбирается единица мага а. Это, по определению, равно молярному объему газа при 0°С и 1 атм. Точное значение этой единицы зависит от природы рассматриваемого газа, но составляет приблизительно 22,4×10 см * / моль. И недавно, Б часто представлены непосредственно в СМ ^ / моль.

Для газа, который немного отличается от идеального, достаточно ограничить его первыми 2 участками разложения. Людмила Фирмаль

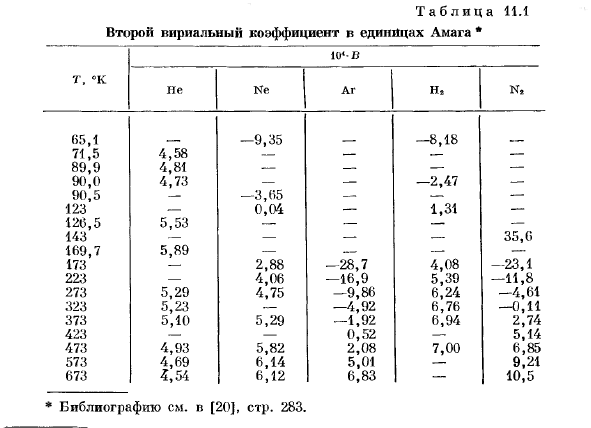
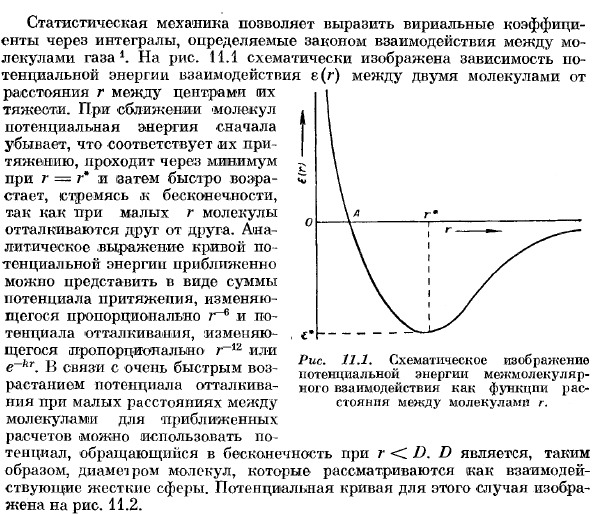
Внутри таблицы. 11.1 показано значение 2-го вириального коэффициента для некоторых нормальных газов в зависимости от температуры. 2-й вириальный коэффициент при низких температурах отрицательный, он увеличивается с температурой и становится положительным при высоких температурах. Температура при B = 0 называется температурой кипения. В статистической механике вириальный коэффициент может быть выражен в интегралах, которые определяются законом взаимодействия молекул газа 1.На рис. 11.1 схематично показана зависимость потенциальной энергии взаимодействия E (g)между 2 молекулами от расстояния r между центрами их притяжения. — При приближении молекулы сначала уменьшается потенциальная энергия. Это соответствует их притяжению и проходит минимальное значение при r = r * l, а затем быстро возрастает.

Аналитическое выражение потенциальной энергии кривой можно приближенно представить в виде суммы привлекательный потенциал, который изменяется пропорционально R-6 и отталкивающий потенциал, который изменяется пропорционально р〜р или Е〜кг. Очень быстро Рисунок 11.1. схематическое представление потенциальной энергии межмолекулярного взаимодействия как функции расстояния между молекулами g. Для приближенных расчетов можно использовать потенциал до бесконечности в растении r ® .

Из показаний B (T) при различных температурах находим e ® , особенно r *и минимальную глубину e. дело в том, что B (T) отрицательно при низких температурах и положительно при высоких температурах заключается в том, что интегральное значение уравнения низкой температуры (11.15) в значительной степени определяется значением R, где e ® отрицательно, а при высоких температурах e ® положительно, область r играет важную роль. Формула для 3-го вириального коэффициента была получена de Boerom2 и Montroll. М и 3 основная свободная энергия ослабляет нсидеалпого газа, что выражается во втором вириальном коэффициенте. Применяя (7.11) и (11.14), получаем Гонка 11.2.

Принципиальная схема потенциальной энергии межмолекулярного взаимодействия (приближение твердой сферы). (11.16) (11.17） Химический потенциал идеального газа определяется по формуле (10.11 Где p16-давление, создаваемое идеальным газом n моль объема T7, so= hRT / ’ V. By подставляя эти выражения для (11.17)、 Широта / ЗРТ * 2 РТРС с = ХТ(г)+ RTln-+. (11.18） Молярная энтропия газа определяется по формуле S 1 (dF, a lH / m dB Где s и d-энтропия тех же T и V, Если газ ведет себя как идеальный газ. Это значение может быть вычислено по формуле (11.19), если известно уравнение состояния и$измеряется калорически (см. Главу 9). таким образом, было найдено исправление, которое использовалось в численных расчетах Sec. JX.

Вместо разложения ряда давлений газа по степеням 1 / y объем газа можно представить в виде ряда стенок. В = ^(1 + б ’п + с’ Р2 + …(11.20).） Где, B’, C1… — функция температуры. Для неидеальных газов вы можете игнорировать все термины, начиная с p2, и вычислить свободную энергию Гиббса. ДФР = шь’/’ / / >、* В-В [Д = firmb И согласно (11.8)、 С. С. Г (т, п, н)= КЦ ^(л р, п)+ м ж «нртб» ’ДП = Г(Т, Пина)+пПТВ’р. ^ п *(11.21） Для однокомпонентных систем Г = п я,(11.22） И затем… li (T, p)= p * BT, p)+ R TV’R. используйте (11.23) (10.11), чтобы получить p = ^ t(71) 4-R7-In p + bBTp. (11.24） Коэффициент (11.20)/?’, С ’ г…

Может быть выражен вириальным коэффициентом формулы (-11.13).Это можно легко проверить на примере 2-го дополнительного коэффициента. Из уравнения (d ’ 1.13)、 R T v С другой стороны, (11.20) ПВ = 1 + и P +. (л, б Р Т Если вы игнорируете членов высшего порядка、 Б = р б ’ Ри. Итак, используя правильное приближение, вы можете написать: C = попадание. В этом приближении вместо (11.20)、 R5T /. 。 П. С. Или В = ВЛД + Б Таким образом, 2-й вириальный коэффициент приблизительно равен разнице между молярным объемом фактического газа и идеального газа при одинаковой температуре и давлении. Наконец, рассмотрим смесь 2 слабых и неидеальных газов, которые не взаимодействуют химически. Формулу (11.14) следует записать в более общем виде, так как необходимо учитывать взаимодействие между идентичными и разными молекулами. ю | л р. г р = ±(Vishch + 2Vapm + Вла).

Фактор B относится к взаимодействию между молекулами типа 1, # 12-к взаимодействию между неравными молекулами 1 и 2, а Vuj-к взаимодействию между молекулами типа 2.При переходе к мольной концентрации 、 Р = + 2JW * + м ^). (11.27） к V ^ Если мы сравним полученную формулу с (11.14), то увидим, что 2-й коэффициент вири-ал смеси можно определить как функцию 2-го порядка от молярной доли. Б = Бин + 2Bi2xtx2 + BiXxi(11.28） Следует подчеркнуть, что для определения 2-го вириального коэффициента смеси недостаточно знать вириальный коэффициент каждого чистого газа, а также необходимо знать дополнительно.

В этом случае коэффициенты в ч, статистической механики вытекает уравнения, например, (11.15) N 0 КТГ(Т)= — $(1-е-MrVkT)^(11.29） И Где eig ® — энергия взаимодействия между молекулами 1 и 2.So по крайней мере, как правило, исследование вириального коэффициента двойной газовой смеси позволяет определить не только энергию взаимодействия En и 822 между молекулами одного типа, но и энергию 6i2.Однако в этом направлении проделано мало работ2.

Как и раньше, вы можете найти свободную энергию смеси. Людмила Фирмаль

/ «=я- + кг * »» ’(11.30） И химический потенциал обоих ингредиентов： 1 * 1 = я я = | * я + 2Р » — й —- V dhz) Tf v>Пж ^ V Из и _ _ _ Впщ + V9Up2 ！12. Ф-О Г ИД Л — М-4- = () = М2 + 2R71″ DN2 по)Т, Т (11.31） Используя последнее уравнение (10.34) t, можно также придать следующий вид: Я… = г(т)+ Р71 в + 2RT (11.32)） В. 1 Фаулер и Гуггенхайм [20), стр. 2. М. См. Newitt. Конструкция установки высокого давления (Оксфорд.1940); И. А. Beafr-галстук, У. Stokmayer. Ж. Chcm. Физика., 10, 473(1942); K. J. Lumbeck, A. J. II. Boerboom Physica, 17, 7G(1951).