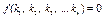В каком случае применяется теория подобия исследуемые процессы описываются похожими уравнениями (8 видео)

I. Дать определение критерия подобия

1. Размерная величина, характеризующая состояние исследуемого процесса.

2. Величина, определяющая связь между параметрами исследуемого процесса.

3. Средняя мера относительной интенсивности двух физических эффектов, существенных для исследуемого процесса.

4. Оператор математической модели исследуемого процесса.

II. В каком случае применяется теория подобия?

1. При отсутствии математического описания исследуемого процесса.

2. Исследуемые процессы описываются похожими уравнениями.

3. Имеется математическое описание исследуемого процесса в виде дифференциальных уравнений.

4. Имеются математическое описание исследуемого процесса в виде дифференциальных уравнений и условия однозначности.

III. В каком случае применяется метод анализа размерностей?

1. При отсутствии математического описания исследуемого процесса.

2. Исследуемые процессы описываются похожими уравнениями.

3. Имеется математическое описание исследуемого процесса в виде дифференциальных уравнений.

IV. В чем заключается полное гидродинамическое подобие?

1. Выполнение только условия геометрического подобия.

2. Выполнение только условия динамического подобия.

3. Необходимо выполнение условий геометрического и кинематического подобия.

4. Необходимо выполнение условий геометрического, кинематического и динамического подобия.

V. В чем заключается физический смысл числа Эйлера?

1. Величина, пропорциональная отношению сил тяжести к силам инерции.

2. Величина, пропорциональная отношению сил инерции к силам вязкого трения.

3. Величина, пропорциональная отношению сил инерции к силам давления.

4. Величина, пропорциональная отношению сил давления к силам инерции.

VI. В чем заключается физический смысл числа Рейнольдса?

1. Величина, пропорциональная отношению сил инерции к силам вязкого трения.

2. Величина, пропорциональная отношению сил вязкого трения к силам инерции.

3. Величина, пропорциональная отношению сил тяжести к силам инерции.

4. Величина, пропорциональная отношению сил поверхностного натяжения к силам инерции.

VII. В чем заключается физический смысл чисел Маха и Коши?

1. Величина, пропорциональная отношению сил инерции к силам упругости.

2. Величина, пропорциональная отношению сил упругости к силам инерции.

3. Величина, пропорциональная отношению сил поверхностного натяжения к силам упругости.

4. Величина, пропорциональная отношению сил упругости к силам поверхностного натяжения.

VIII. В чем состоит подобие процессов конвективного теплообмена?

1. Подобные процессы должны быть качественно одинаковыми.

2. Условия однозначности должны быть одинаковыми во всем.

3. Одноименные критерии подобия должны иметь одинаковые числовые значения.

4. Выполнение всех выше перечисленных пунктов.

IX. Что характеризует число Нуссельта?

1. Отношение внутреннего термического сопротивления к внешнему термическому сопротивлению теплоотдачи.

2. Соотношение между интенсивностью теплоотдачи и температурным полем в пограничном слое потока.

3. Соотношение сил вязкого трения к силам подъема.

4. Отношение внешнего термического сопротивления теплоотдачи к силам подъема.

X. В чем физический смысл числа Пекле?

1. Отношение конвективного и молекулярного переносов тепла в потоке.

2. Соотношение между интенсивностью теплоотдачи и температурным полем в пограничном слое потока жидкости.

3. Отношение сил тяжести к силам упругости.

4. Характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей.

XI. Что характеризует число Прандтля?

1. Подъемную силу, возникающую в жидкости вследствие разности плотностей.

2. Отношение сил тяжести к силам давления.

3. Меру подобия полей температур и скоростей в конвективном теплообмене.

4. Отношение конвективного и молекулярного переносов тепла в потоке.

XII. Что является необходимым и достаточным признаком подобия вентиляторов?

1. Выполнение условия геометрического подобия.

2. Выполнение условия кинематического подобия.

3. Выполнение условия динамического подобия.

4. Выполнение вышеназванных пунктов и равенство коэффициентов быстродействия.

Содержание

Условия подобия физических процессов.
Сущность теории подобия и анализа размерностей, критериальные уравнения
Теория подобия и критериальные уравнения
🌟 Видео

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Условия подобия физических процессов.

ОСНОВЫ ТЕОРИИ ПОДОБИЯ.

Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. Попытки аналитического решения полной системы уравнений наталкиваются на серьезные трудности. Поэтому большое значение приобретает экспериментальный путь исследования. С помощью эксперимента для определенных значений аргументов можно получить числовые значения искомых переменных и затем подобрать уравнения, описывающие результаты опытов. Однако при изучении столь сложного процесса, как конвективный теплообмен, не всегда легко проводить и опытное исследование.

Для исследования влияния на процесс какой – либо величины остальные нужно сохранять неизменными, что не всегда возможно или затруднительно из-за большого количества переменных. Кроме того, при этом нужно быть уверенными, что результаты, получаемые с помощью какой-либо конкретной установки (модели ), можно перенести на другие аналогичные процессы (образец). Эти трудности помогает разрешить теория подобия. С помощью теории подобия размерные физические величины можно объединить в безразмерные комплексы, причем так, что комплексов будет меньше числа величин, из которых составлены эти комплексы. Полученные безразмерные комплексы можно рассматривать как новые переменные.

При введении в уравнения безразмерных комплексов число величин под знаком искомой функции формально сокращается, что упрощает исследование физических процессов. Кроме того, новые безразмерные переменные отражают влияние не только отдельных факторов, но их совокупности, что позволяет легче определить физические связи в исследуемом процессе.

Теория подобия устанавливает также условия, при которых результаты лабораторных исследований можно распространить на другие явления, подобные рассматриваемому.

Для практического исследования выводов теории подобия необходимо уметь приводить к безразмерному виду математические описания изучаемых процессов.

Имеется несколько методов выполнения этой операции.

Один из них — метод масштабных преобразований.

; ; ; .

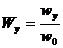
В результате масштабирования получим новые безразмерные переменные:

Помимо приведенных безразмерных величин в уравнение входят безразмерные комплексы, состоящие из различных физических величин. Эти комплексы называются числами подобия.

Первый из этих безразмерных комплексов обозначают:

1) — число Нуссельта,

где — коэффициент теплоотдачи, ;

— коэффициент теплопроводности жидкости, ;

— характеристический размер, м.

Число Нуссельта характеризует конвективный теплообмен между жидкостью и поверхностью твердого тела. Число Нуссельта еще называют безразмерным коэффициентом теплоотдачи.

Несмотря на внешнее сходство с числом Био, рассмотренном при изучении теплопроводности, число Нуссельта существенно отличается от него. В число Bi входит коэффициент теплопроводности твердого тела; в число Nu-коэффициент теплопроводности жидкости. Кроме того, в число Био коэффициент теплоотдачи вводиться как величина, заданная в условиях однозначности, а мы рассматриваем коэффициент теплоотдачи, входящий в Nu, как величину искомую.

2) — число Рейнольдса,

где — скорость движения жидкости, м/с;

— коэффициент кинематической вязкости жидкости, .

Число Рейнольдса характеризует течение жидкости и представляет собой отношение сил инерции к силам вязкости.

Число Рейнольдса является важной характеристикой, как в изотермических, так и в неизотермических процессов течения жидкости.

Третий безразмерный комплекс обозначают:

3) — Число Пекле,

где — число Прандтля.

Число Пекле характеризует собой отношение теплоты, переносимой конвекцией к теплоте, переносимой теплопроводностью.

Число Прандтля характеризует физические свойства жидкости и является мерой подобия полей температур и скоростей.

где – коэффициент температуропроводности жидкости, .

Для капельных жидкостей число изменяется от температуры аналогично вязкости:

То есть при повышении температуры число Прандтля и вязкость уменьшаются.

Для газов число практически не зависит от температуры и давления и является для данного газа величиной постоянной и определяемой атомностью газа:

— для одноатомных газов число = 0,67

— для двухатомных газов число = 0,72

— для трехатомных газов число = 0,80

— для четырехатомных и более число = 1

Для тяжелых и щелочных жидких металлов число Прандтля = 0,005 0,05.

Малые значения числа Pr жидких металлов объясняется высокой теплопроводностью последних.

4) — Число Грасгофа,

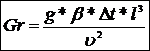
где — коэффициент объемного расширения;

— разность температуры между стенкой и жидкостью.

Оно характеризует соотношение подъемной силы, возникающей в результате разности плотностей жидкости к силам молекулярного трения.

5) — Число Архимеда,

где и — плотности нагретой и холодной жидкости,

Число Архимеда представляет собой модификацию числа Грасгофа. Если =const, .

Уравнения подобия

Полученные безразмерные комплексы можно рассматривать как новые переменные. Их можно разбить на 3 группы:

1. независимые переменные: X, Y

2. зависимые:

3. постоянные величины (они состоят из условий однозначности): .

Кроме того безразмерные переменные можно разделить на две большие группы:

1.Определяемые величины-это числа, в которые входят искомые зависимые ,

следовательно, определяемыми являются

2.Определяющие величины — это числа, целиком составленные из независимых переменных и постоянных величин, входящих в условия однозначности: X,Y,Re,Pr,Pe и Gr.

Уравнением подобия называется зависимость между каким-либо определяемым числом подобия и другими определяющими числами.

Условия подобия физических процессов.

Выражаются тремя теоремами подобия:

Первая теорема подобия (теорема Ньютона) – подобные процессы должны быть качественно одинаковыми, то есть они должны иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями, а также иметь одинаковые числа подобия, т.е.:

Вторая теорема подобия (теорема Бэкингема) – зависимость между переменными, характеризующими какой-либо процесс может быть представлен в виде уравнения подобия. Уравнения подобия для подобных между собой процессов одинаковы. Зависимости между физическими параметрами, характеризующими какое либо явление, могут быть представлены методами масштабных преобразований, анализа размерностей или др.

Третья теорема подобия (теорема Кирпичева и Гухмана). Необходимым условием и достаточным условием подобия физических явлений является подобие условий однозначности (заданных условий) при равенстве чисел подобия , составленных из условий однозначности. Более конкретно смысл третьей теоремы подобия формулируется так.

1.Подобные явления происходят в геометрически подобных системах и описываются подобными уравнениями.

2.Для теплового подобия необходимо наличие физического подобия движения жидкостей.

3.При указанных условиях подобны те явления, для которых подобны условия однозначности, а числа подобия, составленные из условий однозначности, численно равны.

Необходимой предпосылкой теории подобия является математическое описание изучаемого процесса в виде дифференциальных уравнений и условий однозначности.

Видео:Методы исследования технологических процессов. Теория подобия. Виды подобияСкачать

Сущность теории подобия и анализа размерностей, критериальные уравнения

Теория подобия — синтетический метод исследования явлений, учение о методах научного обобщения экспериментов. Он дает возможность использовать преимущество экспериментального и аналитического методов и одновременно устранять их недостатки.

Теория подобия базируется на трех основных теоремах, которые отвечают на три основных практических вопроса: а) какие величины необходимо измерять при экспериментальном исследовании явления? б) как обрабатывать результаты эксперимента, чтобы иметь возможность обобщать опытньк данные для всех подобных явлений? в) какие явления подобны изучаемому?

Для подобия физических явлений необходимо соблюдение геометрического подобия систем (аппаратов) в которых зги явления протекают.

Геометрическое подобие. У подобных геометрических фигур отношение сходственных сторон одинаковы. Фигуры отличаются друг от друга только масштабом и могут быть получены одна из другой умножением сходственных сторон на некоторый постоянный множитель (константа подобия).

Физическое подобие. Физические явления называют подобными, если они происходят в физически подобных системах и если у них во всех сходственных точках в любые сходственные моменты времени отношения одноименных величин равны соответствующим константам подобия (температуры, скорости и др.)

Первая теорема подобия, при подобии систем всегда могут быть найдены такие безразмерные комплексы величин (критерий подобия), которые для сходственных точек данных систем одинаковы по величине, т.е. подобные явления характеризуются численно равными критериями подобия. Критерий ньютона — главный критерий механического подобия и характеризует отношение импульса действующей на частицу силы к силе инерции. Эта теорема устанавливает, какие величины следует измерять при проведении опытов, результаты которых требуется обобщать: надо измерять те величины которые входят в критерии подобия.

Вторая теорема подобия: Решение любого дифференциального уравнения, связывающего между собой переменные, влияющие на процесс может быть представлено в виде зависимости между безразмерными комплексами этих величин, т е между критериями подобия..

Если обозначить критерии подобия через k₀,k_ltk_2i. k_rt, то решение дифференциального уравнения может быть представлено в виде: к₀ = Ск» 1 к? г , где С,т,,т₂. т_я — постоянные, определяемые экспериментально, например в модельных условиях. Такие уравнения называют уравнениями в обобщенных переменных (обобщенными или критериальными уравнениями). Для получения такогс уравнения необходимо решить следующие вопросы: 1) сколько критериев подобия должно входить критериальное уравнение, которым описывается интересующее нас явление? 2) что собой представляют критерии, которые должны входить в критериальное уравнение? 3) как определить значение постоянны> коэффициентов и показателей степени в критериальных уравнениях? На первый вопрос отвечает пи-теорема: всякое уравнение, связывающее N физических и геометрических величин, размерность которых выражена через п основных единиц измерения, можно преобразовать в уравнение подобия, связывающее п критериев: пи=п -N -п

Второй вопрос — выбор способа получения критериев, входящих в критериальное уравнение. Существует три способа получения критериев: а) из известных критериев-комплексов; б) из дифференциальные уравнений; в) методом анализа размерностей. Три способа

Третья теорема подобия. Она устанавливает необходимые условия для того, чтобы явления оказались подобными друг другу. Формулировка подобны те явления, условия однозначности которых подобны, а критерии подобия, составленные № уравнений однозначности, численно равны. Из формулировки следует, подобные явления протекают е геометрически подобных системах; граничные условия подобны; численные значения коэффициентов и физических параметров известны; для рассматриваемого явления можно составить дифференциальные

равнения, для которых установлена единственность решения. Третья теорема устанавливает условием подобия равенство критериев, составленных только из тех величин, которые входят в условие однозначности. Такие критерии называют определяющими.

Видео:Основы теории подобияСкачать

Теория подобия и критериальные уравнения

Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. Попытки аналитического решения полной системы уравнений наталкиваются на серьезные трудности. Поэтому большое значение приобретает экспериментальный путь исследования. Однако при изучении столь сложного процесса, как конвективный теплообмен, не всегда легко проводить и опытное исследование.

Для исследования влияния на процесс какой-либо одной величины остальные нужно сохранять неизменными, что не всегда возможно или затруднительно из-за большого количества переменных. Кроме того, нужно быть уверенным, что результаты, получаемые с помощью какой-либо конкретной установки (модели), можно перенести и на другие аналогичные процессы (образец). Эти трудности помогает разрешить теория подобия. С помощью теории подобия размерные физические величины можно объединить в безразмерные комплексы, причем так, что число комплексов будет меньше числа величин. Полученные безразмерные комплексы можно рассматривать как новые переменные.

При введении в уравнения безразмерных комплексов число величин под знаком искомой функции формально сокращается, что упрощает исследование физических процессов.

Теория подобия устанавливает также условия, при которых результаты лабораторных исследований можно распространить на другие явления, подобные рассматриваемому. Ввиду этого теория подобия является теоретической базой эксперимента, но не только. Теория подобия является важным подспорьем теоретических исследований. Хотя методами теории подобия вид искомой функции не может быть определен, эта теория облегчает в ряде случаев анализ процесса и описание полученных результатов.

Для практического использования выводов теории подобия необходимо уметь приводить к безразмерному виду математические описания изучаемых процессов.

Имеется несколько методов, и один из них — метод масштабных преобразований.

независимые переменные: х, у.

зависимые переменные:

постоянные величины: и др. Для определенной задачи они являются постоянными.

Таким образом, искомые зависимые переменные 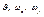зависят от большого числа величин: они являются функцией независимых переменных и постоянных величин.

В качестве масштабов удобно принять постоянные величины .

; ; ; ; , тогда

; ; ; ; .

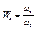
Помимо безразмерных величин и безразмерных координат X, Y, составленных из однородных физических величин, в уравнения входят также безразмерные комплексы, состоящие из разнородных физических величин.

Безразмерные соотношения параметров характеризующих процесс, имеющие у подобных явлений в сходственных точках численно одинаковые значения называются числами подобия.

1). У подобных явлений числа подобия численно одинаковы.

2). Интеграл дифференциальной функции (или системы уравнений) может быть представлен как функция чисел дифференциального уравнения.

3). Подобны те явления, условия однозначности которых подобны, и числа подобия, составленные из условия однозначности, численно одинаковы.

Условия однозначности: Явление, протекающее в геометрически подобных системах; для рассматривания явления можно составить дифференциальные уравнения; установлены существование и единственность решения уравнений при заданных граничных условиях; известны числовые значения коэффициентов и физических параметров.