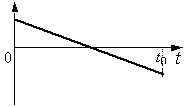
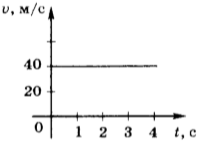
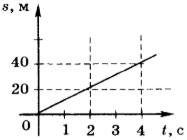
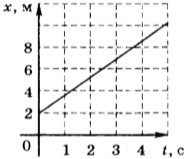
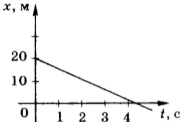
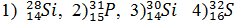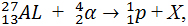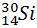Ученик исследовал движение бруска по наклонной плоскости. Он определил, что брусок, начиная движение из состояния покоя, проходит 20 см с ускорением 2,6 м/с 2 . Установите соответствие между физическими величинами, полученными при исследовании движения бруска (см. левый столбец), и уравнениями, выражающими взаимосвязи этих величин, приведёнными в правом столбце.
А) зависимость пути, пройденного бруском, от времени
Б) зависимость модуля скорости бруска от пройденного пути
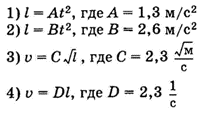
- Отзыв
- Вопрос 2
- Текст вопроса
- Отзыв
- Вопрос 3
- Текст вопроса
- Отзыв
- Вопрос 4
- Текст вопроса
- ЕГЭ по физике: разбираем задания с учителем
- Задание 1
- Решение
- Задание 2
- Решение
- Задание 3
- Решение
- Задание 4
- Решение
- Задание 5
- Решение
- Задание 6
- Решение
- Задание 7
- Решение
- Задание 8
- Решение
- Задание 9
- Решение
- Задание 10
- Решение
- Задание 11
- Решение
- Задание 12
- Решение
- Задание 13
- Решение
- Задание 14
- Решение
- Задание 15
- Решение
- Задание 16
- Решение
- Задание 17
- Решение
- Задание 18
- Решение
- Задание 19
- Решение
- Задание 20
- Решение
- Задание 21
- Решение
- Задание 22
- Решение
- Задание 23
- Решение
- Задание 24
- Задание 25
- Решение
- Задание 26
- Решение
- Задание 27
- Решение
- Задание 28
- Решение
- Задание 29
- Решение
- Задание 30
- Решение
- Задание 31
- Решение
- Равномерное прямолинейное движение
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- 🔍 Видео
Отзыв
Видео:[ОГЭ] Установите соответствие между графиками функций и формулами, которые их задаютСкачать
![[ОГЭ] Установите соответствие между графиками функций и формулами, которые их задают](https://i.ytimg.com/vi/TI55U5oNiyc/0.jpg)
Вопрос 2
Текст вопроса
BB2089 Установите соответствие между зависимостью координаты тела от времени (все величины выражены в СИ) и значениями проекций его начальной скорости и ускорения.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Отзыв
Видео:💯 РЕШЕНИЕ ВАРИАНТОВ №5 и №6 ИЗ НОВОГО СБОРНИКА ДЕМИДОВОЙ | ФИЗИКА ЕГЭ 2024 | УМСКУЛСкачать

Вопрос 3
Текст вопроса
0A5828 Установите соответствие между зависимостью координаты тела от времени (все величины выражены в СИ) и значениями проекций его начальной скорости и ускорения.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
НАЧАЛЬНАЯ СКОРОСТЬ, УСКОРЕНИЕ
Отзыв
Видео:Все типы 1 задание | Физика ЕГЭ 2024 | УмскулСкачать

Вопрос 4
Текст вопроса
3ACBC6 Ученик исследовал движение бруска по наклонной плоскости. Он определил, что брусок, начиная движение из состояния покоя, проходит 20 см с ускорением 2,6 м/с 2 .
Установите соответствие между физическими величинами, полученными при исследовании движения бруска (см. левый столбец), и уравнениями, выражающими эти зависимости, приведёнными в правом столбце. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
А) зависимость пути, пройденного бруском,
от времени
l = Аt 2 , где А = 1,3 м/с 2
Б) зависимость модуля скорости бруска
от пройденного пути
l = Вt 2 , где В = 2,6 м/с 2
Видео:Графики в механике | ФИЗИКА ЕГЭСкачать

ЕГЭ по физике: разбираем задания с учителем
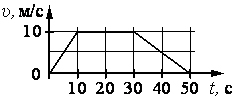
Задание 1
На рисунке представлен график зависимости модуля скорости от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 10 до 30 с.
Ответ: ____________________ м.
Решение
Путь, пройденный автомобилем в интервале времени от 10 до 30 с проще всего определить как площадь прямоугольника, сторонами которого являются, интервал времени (30 – 10) = 20 c и скорость v = 10 м/с, т.е. S = 20 · 10 м/с = 200 м.
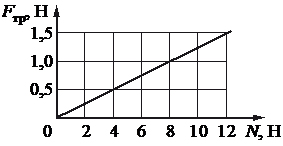
Задание 2
На графике приведена зависимость модуля силы трения скольжения от модуля силы нормального давления. Каков коэффициент трения?
Решение
Вспомним связь между двумя величинами модулем силы трения и модулем силы нормального давления: Fтр= μ N (1) , где μ – коэффициент трения. Выразим из формулы (1)
| μ = | Fтр | (2) |
| N |
На графике найдем точку, для которой можно точно определить координаты. Это в нашем случае может быть Fтр = 1,0 Н, N = 8 Н, тогда
| μ = | 1,0 H | = 0,125 |
| 8 H |
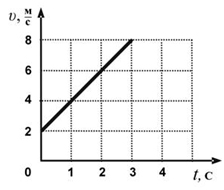
Задание 3
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости модуля скорости тела от времени. Какую мощность развивает эта сила в момент времени t = 3 c?
Решение
Для определения мощности силы по графику определим чему равен модуль скорости в момент времени 3 с. Скорость равна 8 м/с. Используем формулу для расчета мощности в данный момент времени: N = F · v (1), подставим числовые значения. N = 2 Н · 8 м/с = 16 Вт.
Задание 4
Деревянный шарик ( ρ ш = 600 кг/м 3 ) плавает в растительном масле ( ρ м = 900 кг/м 3 ). Как изменится выталкивающая сила, действующая на шар и объем части шара, погруженной в жидкость если масло заменить на воду ( ρ в = 1000 кг/м 3 )
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Выталкивающая сила, действующая на шарик
Объем части шарика, погруженной в жидкость
Решение
Так как плотность материала шарика ( ρ ш = 600 кг/м 3 ) меньше плотности маслa ( ρ м = 900 кг/м 3 ) и меньше плотности воды ( ρ в = 1000 кг/м 3 ), то шар плавает и в масле и в воде. Условие плавания тела в жидкости заключается в том, что выталкивающая сила F a уравновешивает силу тяжести, то есть F а = Fт. Так как сила тяжести шарика при замене масла на воду не изменилась, то не изменилась и выталкивающая сила.
Выталкивающую силу можно вычислить по формуле:
где Vпчт – объем погруженной части тела, ρ ж – плотность жидкости, g – ускорение свободного падения.
Выталкивающие силы в воде и в масле равны.
Плотность масла меньше плотности воды, следовательно, чтобы выполнялось равенство (2) необходимо, чтобы объем части шарика, погруженной в масло Vмпчт, был больше объема части шарика, погруженной в воду Vвпчт. Значит при замене масла на воду, объем части шарика, погруженной в воду уменьшается.
Выталкивающая сила, действующая на шарик
Объем части шарика, погруженной в жидкость
Задание 5
Шарик брошен вертикально вверх с начальной скоростью 
ГРАФИКИ
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А)
Б)
1)
2)
проекция скорости шарика
3)
проекция ускорения шарика
4)
модуль силы тяжести, действующей на шарик
Решение
Определим по условию задачи характер движения шарика. Учитывая, что шарик движется с ускорением свободного падения, вектор которого направлен противоположно выбранной оси, уравнение зависимости проекции скорости от времени, будет иметь вид: v1y = vy – gt (1) Скорость шарика уменьшается, и в наивысшей точке подъема равна нулю. После чего шарик начнет падать до момента t0 – всего времени полета. По величине скорость шарика в момент падения будет равна v, но проекция вектора скорости будет отрицательна, так как направление оси y и вектора скорости противоположны. Следовательно график по буквой А, соответствует зависимости по номером 2) проекции скорости от времени. Графику под буквой Б) соответствует зависимость под цифрой 3) проекция ускорения шарика. Так как ускорение свободного падения у поверхности Земли можно считать постоянным, то графиком будет прямая линия, параллельная оси времени. Так как вектор ускорения и направление не совпадают по направлению, то проекция вектора ускорения отрицательная.
Полезно исключить ответы неверные. Если движение равнопеременное, то графиком зависимости координаты от времени, должна быть парабола. Такого графика нет. Модуль силы тяжести, этой зависимости должен соответствовать график расположенный выше оси времени.
Задание 6
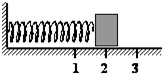
Груз изображенного на рисунке пружинного маятника совершает гармонические колебания между точками 1 и 3. Как меняется кинетическая энергия груза маятника, скорость груза и жесткость пружины при движении груза маятника от точки 2 к точке 1
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Кинетическая энергия груза
Решение
Груз на пружине совершает гармонические колебания между точками 1 и 3. Точка 2 соответствует положению равновесия. Согласно закону сохранения и превращения механической энергии при переходе груза из точки 2 к точке 1, энергия не исчезает, она превращается из одного вида в другой. Полная энергия сохраняется. В нашем случае увеличивается деформация пружины, возникающая сила упругости будет направлена к положению равновесия. Поскольку сила упругости направлена против скорости движения тела, то она тормозит его движение. Следовательно, скорость шарика уменьшается. Кинетическая энергия уменьшается. Увеличивается потенциальная энергия. Жесткость пружины в ходе движения тела не изменяется.
Кинетическая энергия груза
Задание 7
Установите соответствие между зависимостью координаты тела от времени (все величины выражены в СИ) и зависимостью проекции скорости от времени для того же тела. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами
КООРДИНАТА
СКОРОСТЬ
А)
Б)
1)
2)
3)
4)
Решение
Полезно записать закон движения (зависимость координаты тела от времени) в общем виде:
| х = x0 + vxt + | a x · t 2 | (1), |
| 2 |
где х0 – начальная координата тела; vx – проекция вектора скорости на выбранную ось; a x – проекция вектора ускорения на выбранную ось; t – время движения.
Для тела А запишем: начальная координата х0 = 10 м; vx = –5 м/с; a x = 4 м/с 2 . Тогда уравнение проекции скорости от времени будет иметь вид:
Для нашего случая vx = 4t – 5.
Для тела Б запишем принимая во внимание формулу (1): х0 = 5 м; vx = 0 м/с; a x = –8 м/с 2 . Тогда уравнение проекции скорости от времени для тела Б запишем vx = –8t.
Задание 8
В результате нагревания неона абсолютная температура газа увеличилась в 4 раза. Во сколько раз изменилась при этом средняя кинетическая энергия теплового движения его молекул?
Решение
Необходимо вспомнить связь средней кинетической энергии теплового движения молекул и температуры.
| Ek = | 3 | kT (1), |
| 2 |
где k – постоянная Больцмана, T – температура газа в Кельвинах. Из формулы видно, что зависимость средней кинетической энергии от температуры прямая, то есть во сколько раз изменяется температура, во столько раз изменяется средняя кинетическая энергия теплового движения молекул.
Задание 9
Газ в некотором процессе отдал количество теплоты 35 Дж, а внутренняя энергия газа в этом процессе, увеличилась на 10 Дж. Какую работу совершили над газом внешние силы?
Решение
В условии задачи идет речь о работе внешних сил над газом. Поэтому первый закон термодинамики лучше записать в виде:
Где ∆U = 10 Дж – изменение внутренней энергии газа; Q = –35 Дж – количество теплоты отданное газом, Aв.с – работа внешних сил.
Подставим числовые значения в формулу (1) 10 = –35 + Ав.с; Следовательно работа внешних сил будет равна 45 Дж.
Задание 10
Парциальное давление водяных паров при 19° С было равно 1,1 кПа Найти относительную влажность воздуха, если давление насыщенного пара при этой температуре равно 2,2 кПа?
Решение
По определению относительной влажности воздуха
| φ = | Pв.п | · 100% (1), |
| Pн.п |
φ – относительная влажность воздуха, в процентах; Pв.п – парциальное давление водяного пара, Pн.п – давление насыщенного пара при данной температуре.
Подставим числовые значения в формулу (1).
| φ = | 1,1 · 10 3 Па | · 100% = 50% |
| 2,2 · 10 3 Па |
Задание 11
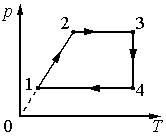
Изменение состояния фиксированного количества одноатомного идеального газа происходит по циклу, показанному на рисунке.
Установите соответствие между процессами и физическими величинами (∆U – изменение внутренней энергии; А – работа газа), которые их характеризуют.
К каждой позиции из первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры по соответствующими буквами.
ПРОЦЕССЫ
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А)
Б)
1)
2)
Решение
Данный график можно перестроить в осях PV или разобраться с тем, что дано. На участке 1–2, изохорный процесс V = const; Растет давление и температура. Газ работу не совершает. Поэтому A = 0, Изменение внутренней энергии больше нуля. Следовательно, верно записаны физические величины и их изменения под номером 4) ΔU > 0; A = 0. Участок 2–3: изобарный процесс, P = const; увеличивается температура и увеличивается объем. Газ расширяется, работа газа A>0, Следовательно, переходу 2–3 соответствует запись под номером 1) ΔU > 0; A > 0.
Задание 12
Идеальный одноатомный газ, находящийся в цилиндре под тяжелым поршнем (трением между поверхностью поршня и цилиндром можно пренебречь), медленно нагревают от 300 К до 400 К. Внешнее давление при этом не изменяется. Затем этот же газ вновь нагревают от 400 К до 500 К, но уже с закрепленным поршнем (поршень не двигается).
Сравните работу газа, изменение внутренней энергии и количество теплоты, полученное газом, в первом и втором процессах.
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Изменение внутренней энергии
Количество теплоты, полученное газом
Решение
Если газ медленно нагревают в цилиндре с незакрепленным тяжелым поршнем, то при неизменном внешнем давлении процесс можно считать изобарным (давление газа не изменяется)
Следовательно, работу газа можно вычислить по формуле:
где A – работа газа в изобарном процессе; P – давление газа; V1 – объем газа в начальном состоянии; V2 – объем газа в конечном состоянии.
Изменение внутренней энергии идеального одноатомного газа вычисляется по формуле:
| ∆U = | 3 | v R∆t (2), |
| 2 |
где v – количество вещества; R – универсальная газовая постоянная; ∆T – изменение температуры газа.
По первому закону термодинамики количество теплоты, полученное газом, равно
Если газ нагревают в цилиндре с закрепленным поршнем, то процесс можно считать изохорным (объем газа не изменяется). В изохорном процессе идеальный газ не совершает работу (поршень не перемещается).
Изменение внутренней энергии равно:
| ∆U = | 3 | v R (T4 – T3) = 150 v R (6) |
| 2 |
Количество теплоты в этом случае: Q = 150 v R (7)
Сравнивая (1) и (5), (2) и (6), (4) и (7) делаем вывод. Работа газа уменьшилась, Изменение внутренней энергии осталось прежним, количество теплоты, полученное газом, уменьшилось.
Изменение внутренней энергии
Количество теплоты, полученное газом
Задание 13
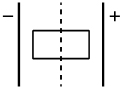
В электрическое поле внесли незаряженный кусок диэлектрика (см. рисунок). Затем его разделили на две равные части (пунктирная линия) и после этого вынесли из электрического поля. Какой заряд будет иметь каждая часть диэлектрика?
- Заряд обеих частей равен нулю;
- Левая часть заряжена положительно, правая – отрицательно;
- Левая часть заряжена отрицательно, правая – положительно;
- Обе части заряжены отрицательно;
- Обе части заряжены положительно.
Решение
Если внести в электрическое поле диэлектрик, (вещество в котором нет свободных электрических зарядов) при обычных условиях, то наблюдается явление поляризации. В диэлектриках заряженные частицы не способны двигаться по всему объему, а могут лишь смещаться на небольшие расстояния относительно своих постоянных положений, электрические заряды в диэлектриках связанные. Если диэлектрик вынести из поля, то заряд обеих частей равен нулю.
Задание 14
Колебательный контур состоит из конденсатора емкостью C и катушки с индуктивности L. Как изменится частота и длина волны колебательного контура, если площадь пластин конденсатора уменьшить в два раза? Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Решение
В задаче говорится о колебательном контуре. По определению периода колебаний возникающих в контуре 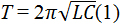
| λ = | c | (2), |
| v |
где v – частота колебаний. По определению емкости конденсатора
где ε 0 – электрическая постоянная, ε – диэлектрическая проницаемость среды. По условию задачи уменьшают площадь пластин. Следовательно, уменьшается емкость конденсатора. Из формулы (1) видим, что уменьшится период электромагнитных колебаний, возникающих в контуре. Зная связь периода и частоты колебаний
| v = | 1 | (4), |
| T |
видим, что частота колебаний увеличивается. А используя формулу (2), заключаем, что длина волны уменьшается.
Задание 15
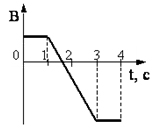
На графике показано как меняется индукция магнитного поля с течением времени в проводящем контуре. В какой промежуток времени в контуре будет возникать индукционный ток.
Решение
По определению индукционный ток в проводящем замкнутом контуре возникает при условии изменения магнитного потока, пронизывающего этот контур.
| Ɛ = | – | ∆ Φ | (1) |
| ∆t |
Закон электромагнитной индукции, где Ɛ – ЭДС индукции, ∆ Φ – изменение магнитного потока, ∆t промежуток времени, в течении которого происходят изменения.
Магнитный поток по условию задачи будет меняться, если меняется индукция магнитного поля. Это происходит в интервале времени от 1 с до 3 с. Площадь контура не изменяется. Следовательно, индукционный ток возникает в случае
- К моменту времени t = 1 с изменение магнитного потока через контур больше нуля.
- Индукционный ток в контуре возникает в интервале от (t = 1 с до t = 3 с)
- Модуль ЭДС индукции, возникающей в контуре, равен 10 мВ.
- изменение магнитного потока через контур от t = 3 c до t = 4 с меньше нуля.
- Индукционный ток равен нулю в промежутки времени от (t = 0 с до t = 1 с) и от (t = 3 с до t = 4 с)
Задание 16
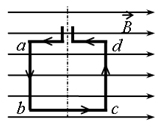
Квадратная рамка расположена в однородном магнитном поле в плоскости линий магнитной индукции (см. рисунок). Направление тока в рамке показано стрелками. Как направлена сила, действующая на сторону ab рамки со стороны внешнего магнитного поля 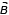
Решение
На рамку с током со стороны магнитного поля действует сила Ампера. Направление вектора силы Ампера определяется мнемоническим правилом левой руки. Четыре пальца левой руки направляем по току стороны ab, вектор индукции В, должен входить в ладонь, тогда большой палец покажет направление вектора силы Ампера.
Ответ: к наблюдателю.
Задание 17
Заряженная частица влетает с некоторой скоростью в однородное магнитное поле перпендикулярно силовым линиям поля. С некоторого момента времени, модуль индукции магнитного поля увеличили. Заряд частицы не изменился.
Как изменилась сила, действующая на движущуюся частицу в магнитном поле, радиус окружности, по которой движется частица, и кинетическая энергия частицы после увеличения модуля индукции магнитного поля?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Сила, действующая на движущуюся частицу в магнитном поле |
| R = | mv | (2), |
| qB |
где m – масса частицы. Следовательно, с увеличением индукции поля, радиус окружности уменьшается.
Сила Лоренца работы не совершает над движущейся частицей, так как угол между вектором силы и вектором перемещения (вектор перемещения направлен по вектору скорости) равен 90°.
Поэтому кинетическая энергия независимо от значения индукции магнитного поля не изменяется.
| Сила, действующая на движущуюся частицу в магнитном поле |
| P = | A | , (1) |
| t |
где P – мощность электрического тока, A – работа электрического тока, t – время, в течение которого по проводнику протекает электрический ток. Работа, в свою очередь, рассчитывается
где I – сила электрического тока, U – напряжение на участке,
| I = | U | , (3) |
| R |
Закон Ома для участка цепи , R сопротивление проводника. Работая с уравнениями, получим, что мощность тока, выделяющаяся на резисторе I 2 R, напряжение на резисторе I R
Задание 19
В результате реакции ядра 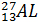
Решение
Pапишем ядерную реакцию для нашего случая:
В результате этой реакции, выполняется закон сохранения зарядового и массового числа. Z = 13 + 2 – 1 = 14; M = 27 + 4 – 1 = 30.
Следовательно, ядро под номером 3)
Задание 20
Период полураспада вещества составляет 18 минут, первоначальная масса 120 мг, Чему будет равна масса вещества через 54 минуты, ответ выразить в мг?
Решение
Задача на использование закона радиоактивного распада. Его можно записать в виде
| m = m02– | t | , (1) |
| T |
где m0 – первоначальная масса вещества, t – время за которое распадается вещество , T – период полураспада. Подставим числовые значения
| m = 120 · 2 – | 54 | = 120 · 2 –3 = 120 | 1 | = 15 (мг) |
| 18 | 8 |
Задание 21
Фотокатод фотоэлемента освещают ультрафиолетовым светом определенной частоты. Как изменяется работа выхода материала (вещества) фотокатода, максимальная кинетическая энергия фотоэлектронов и красная граница фотоэффекта, если частоту света увеличить?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Работа выхода материала фотокатода
Максимальная кинетическая энергия фотоэлектронов
Красная граница фотоэффекта
Решение
Полезно вспомнить определение фотоэффекта. Это явление взаимодействия света с веществом, в результате которого энергия фотонов передается электронам вещества. Различают внешний и внутренний фотоэффект. В нашем случае речь идет о внешнем фотоэффекте. Когда под действием света происходит вырывание электронов из вещества. Работа выхода зависит от материала, из которого изготовлен фотокатод фотоэлемента, и не зависит от частоты света. Поэтому при увеличении частоты ультрафиолетового света, падающего на фотокатод, работа выходане изменяется.
Запишем уравнение Эйнштейна для фотоэффекта:
hv – энергия фотона, падающего на фотокатод, Aвых – работа выхода, Eк – максимальная кинетическая энергия фотоэлектронов, вылетающих из фотокатода под действием света.
Из формулы (1) выразим
следовательно, при увеличении частоты ультрафиолетового света максимальная кинетическая энергия фотоэлектронов увеличивается.
| vкр = | Aвых | , (3) |
| h |
это минимальная частота, при которой еще возможен фотоэффект. Так как работа выхода не изменяется, то и красная граница фотоэффекта для нашего материала не изменяется.
Работа выхода материала фотокатода
Максимальная кинетическая энергия фотоэлектронов
Красная граница фотоэффекта
Задание 22
В мензурку налита вода. Выберите верное значение объема воды, учитывая, что погрешность измерения равна половине цены деления шкалы.
1)
2)
3)
4)
Решение
Задание проверяет умение записывать показания измерительного прибора с учетом заданной погрешности измерений. Определим цену деления шкалы
| с = | 90 мл – 60 мл | = 10 мл; |
| 3 |
Погрешность измерения по условию равна половине цены деления, т.е.
| ∆V = | c | = | 10 мл | = 5 мл. |
| 2 | 2 |
Конечный результат запишем в виде:
Задание 23
Проводники изготовлены из одного и того же материала. Какую пару проводников нужно выбрать, чтобы на опыте обнаружить зависимость сопротивления проволоки от ее диаметра?
1)
2)
3)
4)
Решение
В задание говорится о том, что проводники изготовлены из одного и того же материала, т.е. их удельные сопротивления одинаковые. Вспомним от каких величин зависит сопротивление проводника и запишем формулу для расчета сопротивления:
| R = | p l | (1), |
| S |
где R – сопротивление проводника, p – удельное сопротивление материал, l – длина проводника, S – площадь поперечного сечения проводника. Для того, чтобы выявить зависимость проводника от диаметра нужно взять проводники одинаковой длины, но разного диаметра. Заем, что площадь поперечного сечения проводника определяется как площадь круга:
| S = π | d 2 | (2), |
| 4 |
где d – диаметра проводника. Следовательно, вариант ответа: 3.
Задание 24
Снаряд массой 40 кг, летящий в горизонтальном направлении со скоростью 600 м/с, разрывается на две части массами 30 кг и 10 кг. Большая часть движется в прежнем направлении со скоростью 900 м/с. Определите числовое значение, и направление скорости меньшей части снаряда. В ответ запишите модуль этой скорости.
В момент разрыва снаряда (∆t → 0) действием силы тяжести можно пренебречь и рассматривать снаряд как замкнутую систему. По закону сохранения импульса: векторная сумма импульсов тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Для нашего случая запишем:
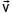
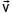
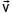
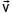
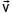
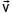
Выберем положительное направление оси Х, совпадающей с направлением скорости снаряда, тогда в проекции на эту ось уравнение (1) запишем:
Выразим из формулы (2) проекцию вектора скорости второго осколка.
| v2x = ( | mvx | – | m1v1x | ); |
| m2 | m2 |
подставим числовые значения.
| v2x = | 40 кг · 600 м/с – 30 кг · 900м/с | = –300 м/с |
| 10 кг |
Меньшая часть снаряда в момент разрыва имеет скорость 300 м/с, направленную в сторону, противоположную первоначальному движению снаряда.
Задание 25
В калориметре находятся в тепловом равновесии 50 г воды и 5 г льда. Какой должна быть минимальная масса болта, имеющего удельную теплоемкость 500 Дж/кг К и температуру 339 К, чтобы после опускания его в калориметр весь лед растаял? Тепловыми потерями пренебречь. Ответ представить в граммах.
Решение
Для решения задачи важно вспомнить уравнение теплового баланса. Если потерь нет, то в системе тел происходит теплопередача энергии. В результате чего, лед плавиться. Первоначально вода и лед находились в тепловом равновесии. Это значит, что начальная температура была 0° С или 273 К. Помним перевод из градусов Цельсия в градусы Кельвина. Т = t + 273. Так как по условию задачи спрашивается о минимальной массе болта, то энергии должно хватить только, чтобы расплавить лед.
где λ – удельная теплота плавления, mл – масса льда, mб – масса болта.
Выразим из формулы (1)
| mб = | λ mл | (2) |
| сб(tб – 0) |
| mб = 3,3· | 105 Дж | · | 5 · 10 –3 кг | = 0,05 кг = 50 г. |
| кг | 500 Дж/кгК (339 – 273) |
Задание 26
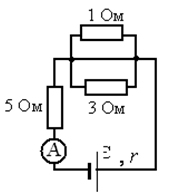
В цепи, показанной на рисунке, идеальный амперметр показывает 6 А. Найдите ЭДС источника, если его внутреннее сопротивление 2 Ом.
Решение
Внимательно читаем условие задачи и разбираемся со схемой. В ней есть один элемент, который можно не заметить. Это пустой провод между резисторами в 1 Ом и 3 Ом. Если цепь будет замкнута, то электрический ток пройдет по этому проводу с наименьшим сопротивлением и через резистор 5 Ом.
Тогда закон Ома для полной цепи запишем в виде:
| I = | ε | (1) |
| R + r |
где – сила тока в цепи, ε – ЭДС источника, R – сопротивление нагрузки, r – внутренне сопротивление. Из формулы (1) выразим ЭДС
ε = 6 A (5 Ом + 2 Ом) = 42 В.
Задание 27
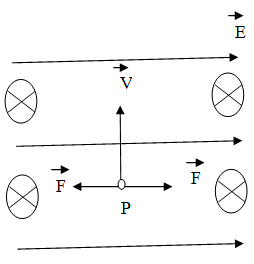
В камере, из которой откачали воздух, создали электрическое поле напряженностью 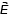
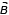
Решение
В решении задачи необходимо остановиться на первоначальном движении протона и на изменении характера движения после изменения индукции магнитного поля. На протон действует магнитное поле силой Лоренца, модуль которой равен Fл = qvB и электрическое поле силой, модуль которой равен Fэ = qE. Поскольку заряд протона положительный, то 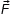
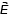
С увеличением индукции магнитного поля будет увеличиваться сила Лоренца. Равнодействующая сил в этом случае будет отлична от нуля и направлена в сторону большей силы. А именно в сторону силы Лоренца. Равнодействующая сила сообщает протону ускорение, направленное влево, траектория протона будет криволинейной, отклоняющейся от первоначального направления.
Задание 28
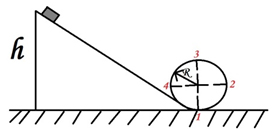
Тело соскальзывает без трения по наклонному желобу, образующему «мертвую петлю» радиусом R. С какой высоты тело должно начать движение, чтобы не оторваться от желоба в верхней точке траектории.
Решение
Нам дана задача о неравномерно переменном движении тела по окружности. В процессе этого движения изменяется положение тела по высоте. Проще решить задачу, используя уравнения закона сохранения энергии и уравнения второго закона Ньютона по нормали к траектории движения. Сделали рисунок. Запишем формулу закона сохранения энергии:
где W2 и W1 – полная механическая энергия в первом и втором положении. За нулевой уровень выберем положение стола. Нас интересуют два положения тела – это положение тела в начальный момент движения, второе – положение тела в верхней точке траектории (это точка 3 на рисунке). В процессе движения на тело действуют две силы: сила тяжести 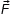
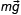
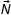
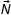
В положение 1: W1 = mgh (3), где m – масса тела; g – ускорение свободного падения; h – высота , с которой тело начинает двигаться.
В положении 2 (точка 3 на рисунке):
| W2 = mg2R + | mv 2 | (4) |
| 2 |
где v – скорость тела в точке 3. Подставляя полученные выражения в формулу (1), получим
| 0 = mg2R + | mv 2 | – mgh, |
| 2 |
В верхней точке петли на тело действует две силы 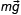
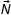
| N + mg = | mv 2 | (6); |
| R |
При уменьшении начальной высоты спуска скорость шарика в верхней точке петли уменьшается и при некотором значении h становится такой, что он пролетает верхнюю точку петли, лишь касаясь желоба. Для этого предельного случая N = 0 и уравнение второго закона примет вид:
| mg = | mv 2 | , т.е. ev 2 = gR (7) |
| R |
Решая уравнения (5) и (7) получим h = 2,5 R
Задание 29
Воздух в комнате объемом V = 50 м 3 имеет температуру t = 27° C и относительную влажность воздуха φ 1 = 30%. Сколько времени τ должен работать увлажнитель воздуха, распыляющий воду с производительностью μ = 2 кг/ч, чтобы относительная влажность в комнате повысилась до φ 2 = 70%. Давление насыщенных паров воды при t = 27° C равно pн = 3665 Па. Молярная масса воды 18 г/моль.
Решение
Приступая к решению задач на пары и влажность, всегда полезно иметь в виду следующее: Если задана температура и давление (плотность) насыщающего пара, то его плотность (давление) определяют из уравнения Менделеева-Клапейрона. Записать уравнение Менделеева-Клапейрона и формулу относительной влажности для каждого состояния.
Для первого случая при φ 1 = 30% парциальное давление водяного пара выразим из формулы:
| φ 1 = | P1 | · 100% (1); |
| Pн |
| P1 = | φ 1Pн | (2). |
| 100% |
Запишем уравнение Менделеева – Клапейрона
| P1V = | m1 | RT (3), |
| M |
где T = t + 273 (К), R – универсальная газовая постоянная. Выразим начальную массу пара, содержащегося в комнате используя уравнение (2) и (3):
| m1 = | φ 1 | MPнV, (4) |
| 100%RT |
аналогично при влажности φ 2 масса пара
| m2 = | φ 2 | MPнV, (5) |
| 100%RT |
Время, которое должен работать увлажнитель воздуха, можно рассчитать по формуле
| τ 2 = | (m2 – m1) | (6) |
| μ |
подставим (4) и (5) в (6)
Подставим числовые значения и получим, что увлажнитель должен работать 15,5 мин.
Задание 30
Определите ЭДС источника, если при подключении к нему резистора с сопротивлением R напряжение на зажимах источника U1 = 10 B, а при подключении резистора 5R напряжение U2 = 20 B.
Решение
Запишем уравнения для двух случаев.
где r – внутреннее сопротивление источника, Ɛ – ЭДС источника.
где U1 и U2 – напряжение на зажимах в первом и втором случае.
Учитывая закон Ома для участка цепи, перепишем уравнения (1) и (3) в виде:
| Ɛ = U1 + | U1– | r (5) |
| R |
| Ɛ = U2 + | U2– | r (6) |
| 5R |
Из уравнения (6) выразим внутреннее сопротивление и подставим в (5)
| r = | ( Ɛ – U2)5R | (7) |
| U2 |
Последняя подстановка для расчета ЭДС. Формулу (7) подставим в (5)
| Ɛ = | 4U1U2 | = | 4 · 10В · 20В | = 27 В. |
| 5U1 – U2 | 5 · 10 В – 20 В |
Задание 31
При освещении пластинки изготовленной из некоторого материала, светом с частотой v 1 = 8 · 1014 Гц, а затем v 2 = 6 · 1014 Гц обнаружилось, что максимальная кинетическая энергия электронов изменилась в 3 раза. Определите работу выхода электронов из этого металла.
Решение
Если частота кванта света, вызывающего фотоэффект, уменьшается, то уменьшается и кинетическая энергия. Поэтому кинетическая энергия во втором случае тоже будет меньше в три раза. Запишем уравнение Эйнштейна для фотоэффекта для двух случаев.
для первой частоты света
| hv2 = A + | Eк | (2) |
| 3 |
для второй частоты света
Решаем уравнения (1) и (2) совместно. Вычтем из (1) (2) и выразим Ек
| Ек = | 3 | h(v1 – v2) (3) – |
| 2 |
формула для кинетической энергии.
Из уравнения (1) выразим работу выхода и подставим вместо кинетической энергии выражение (3)
Видео:Установите соответствие между графиками функций ... | ОГЭ 2017 | ЗАДАНИЕ 5 | ШКОЛА ПИФАГОРАСкачать
Равномерное прямолинейное движение
1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.
Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.
2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.
Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.
Если за время ( t ) тело совершило перемещение ( vec ) , то скорость его движения ( vec ) равна ( vec=frac<vec> ) .
Единица скорости: ( [,v,]=frac ) ; ( [,v,]=frac=1frac ) . За единицу скорости принимается 1 м/с — скорость такого равномерного движения, при котором тело за 1 с совершает перемещение 1 м.
Зная скорость равномерного движения, можно найти перемещение за любой промежуток времени: ( vec=vect ) . Вектор скорости и вектор перемещения направлены в одну сторону — в сторону движения тела.
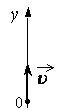
3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.
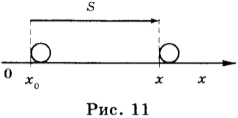
Пусть ( vec ) — перемещение тела (рис. 11). Направим координатную ось ОХ по направлению перемещения. Найдем проекцию перемещения на координатную ось ОХ. На рисунке ( x_0 ) — координата начальной точки перемещения, ( x ) — координата конечной точки перемещения. Проекция перемещения равна разности координат конечной и начальной точек: ( vec_x=x-x_0 ) . С другой стороны, проекция перемещения равна проекции скорости, умноженной на время, т.е. ( vec_x=vec_xt ) . Откуда ( x-x_0=vec_xt ) или ( x=x_0+vec_xt ) . Если начальная координата ( x_0 ) = 0, то ( x=vec_xt ) .
Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.
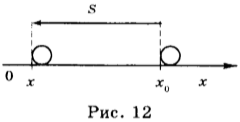
Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае ( x>x_0 ) . Проекция скорости отрицательна, если тело движется против положительного направления оси ОХ (рис. 12). В этом случае ( x .
4. Зависимость координаты от времени можно представить графически.
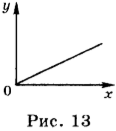
Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: ( x ) = 4 м/с · ( t ) . Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).
Для того чтобы её построить, необходимо иметь две точки: одна из них ( t ) = 0 и ( x ) = 0, а другая ( t ) = 1 с, ( x ) = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.
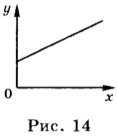
Если в начальный момент времени координата тела ( x_0 ) = 2 м, а проекция его скорости ( v_x ) = 4 м/с, то уравнение движения имеет вид: ( x ) = 2 м + 4 м/с · ( t ) . Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой ( t ) = 0, ( x ) = 2 м (рис. 14).
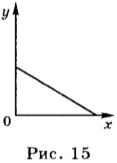
В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: ( x ) = 2 м – 4 м/с · ( t ) . График зависимости координаты такого движения от времени представлен на рисунке 15.
Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.
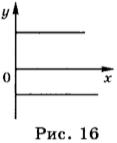
График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.
5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.
Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.
При решении задачи целесообразно придерживаться следующей последовательности действий:
- Кратко записать условие задачи.
- Проанализировать ситуацию, описанную в условии задачи:
— выяснить, можно ли принять движущиеся тела за материальные точки;
— сделать рисунок, изобразив на нём векторы скорости;
— выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела. - Записать в общем виде уравнение движения в векторной форме и для проекций на координатные оси.
- Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости.
- Решить задачу в общем виде.
- Подставить в формулу значения величин и выполнить вычисления.
- Проанализировать ответ.
Применим эту последовательность действий к приведённой выше задаче.
Дано: ( v_1 ) = 15 м/с ( v_2 ) = 12 м/с ( l ) = 270 м. Найти: ( t ) – ? ( x) – ?
Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь
Система отсчёта связана с Землёй, ось ( Ox ) направлена в сторону движения первого тела, начало отсчёта координаты — т. ( O ) — положение первого тела в начальный момент времени.
Начальные условия: ( t ) = 0; ( x_ ) = 0; ( x_ ) = 270.
Уравнение в общем виде: ( vec=vect ) ; ( x=x_0+v_xt ) .
Уравнения для каждого тела с учётом начальных условий: ( x_1=v_1t ) ; ( x_2=l-v_2t ) . В месте встречи тел ( x_1=x_2 ) ; следовательно: ( v_1t=l-v_2t ) . Откуда ( t=fraccdot t ) . Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей: ( x ) = 150 м.
Видео:💯 Решение вариантов №3 и №4 из нового сборника Демидовой | Физика ЕГЭ 2024 | УмскулСкачать

ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?
1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с
2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?
1) 0,25 м
2) 6 м
3) 10 м
4) 150 м
3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — ( v_1 ) и скорости «Пежо» — ( v_2 ) .
1) ( v_1=v_2 )
2) ( v_1=2v_2 )
3) ( 2v_1=v_2 )
4) ( 1,2v_1=10v_2 )
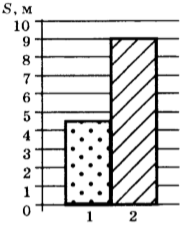
4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости ( v_1 ) и ( v_2 ) .
1) ( v_1=v_2 )
2) ( v_1=2v_2 )
3) ( 3v_1=v_2 )
4) ( 2v_1=v_2 )
5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен
1) 20 м
2) 40 м
3) 80 м
4) 160 м
6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен
1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с
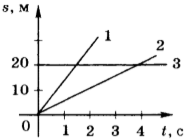
7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости ( v_1 ) , ( v_2 ) и ( v_3 ) движения этих тел.
1) ( v_1=v_2=v_3 )
2) ( v_1>v_2>v_3 )
3) ( v_1
4) ( v_1=v_2 ) , ( v_3
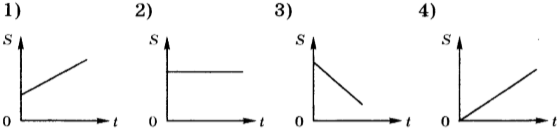
8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?
9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?
1) 9,8 м
2) 6 м
3) 4 м
4) 2 м
10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид
1) ( x=1t ) (м)
2) ( x=2+3t ) (м)
3) ( x=2-1t ) (м)
4) ( x=4+2t ) (м)
11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость
ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит
12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.
1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось
Часть 2
13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?
🔍 Видео
Графики в физике | Физика ЕГЭ 2023 | УмскулСкачать

Задача из ЕГЭ по физике │Анализ графика #1Скачать

🔴 ЕГЭ-2024 по физике. Равномерное и равноускоренное движение. Задания с графикамиСкачать

ВСЯ МЕХАНИКА ЗА 6 ЧАСОВ | ФИЗИКА ЕГЭ 2024 | УМСКУЛСкачать

Задание 7 ЕГЭ по физике. Установление соответствия. Часть 2Скачать

Полный разбор варианта 2022 | Физика ЕГЭ 2023 | УмскулСкачать

Графики зависимости пути и скорости от времениСкачать

💯 Полное решение демоверсии ЕГЭ 2024 по физике | УмскулСкачать

ЕГЭ Физика. Установите соответствие между зависимостью x(t) и V0х и axСкачать

ВСЕ ТИПЫ 6 ЗАДАНИЕ | МЕХАНИКА | РЕШАЕМ ВМЕСТЕ | ЕГЭ ФИЗИКА 2024 | ДЕМИДОВАСкачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Задание 7 ЕГЭ по физике. Установление соответствия. Часть 4Скачать

Физика ЕГЭ 2021,1-8 задание, механика. Решение задач варианта 1 сайта Д. Гущина "Решу ЕГЭ"Скачать

ЕГЭ Физика. Установите соответствие между зависимостью x(t) и зависимостью Vx(t)Скачать