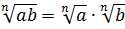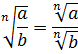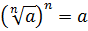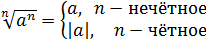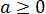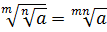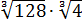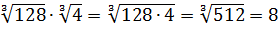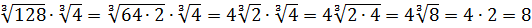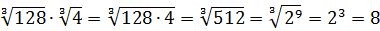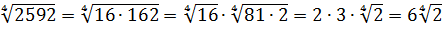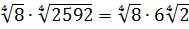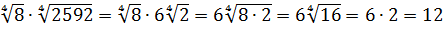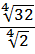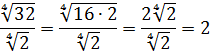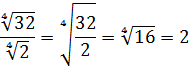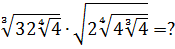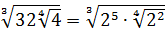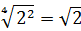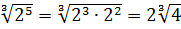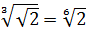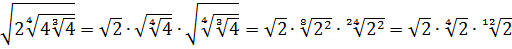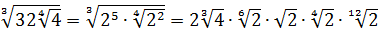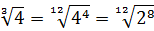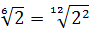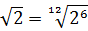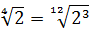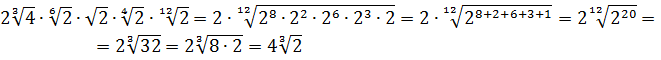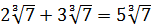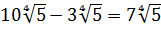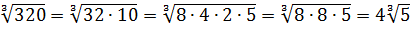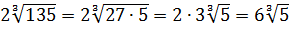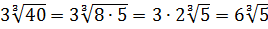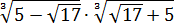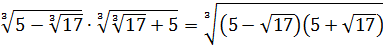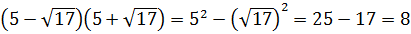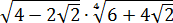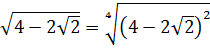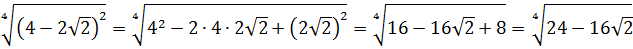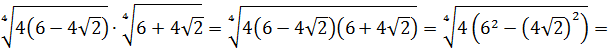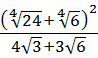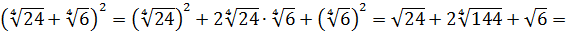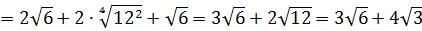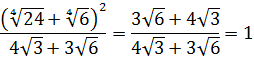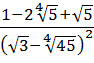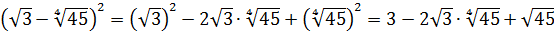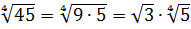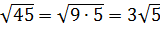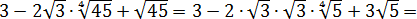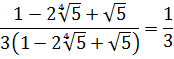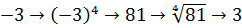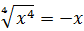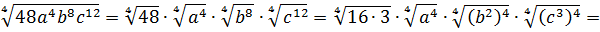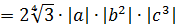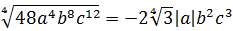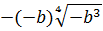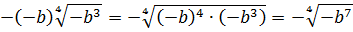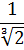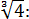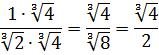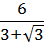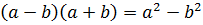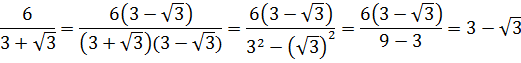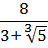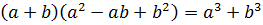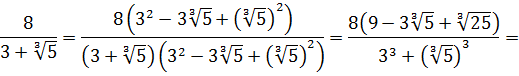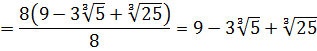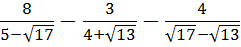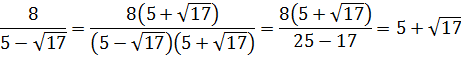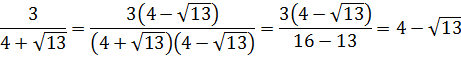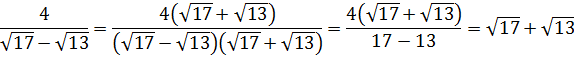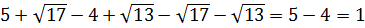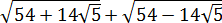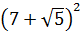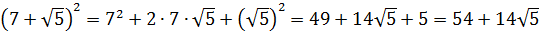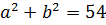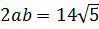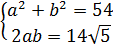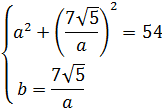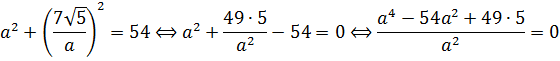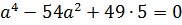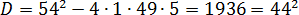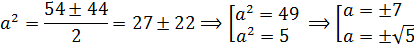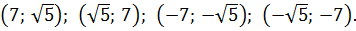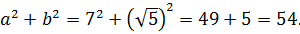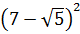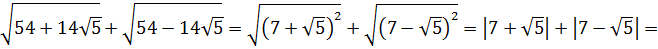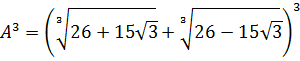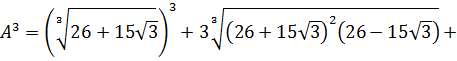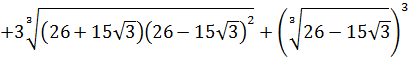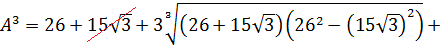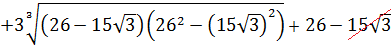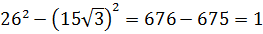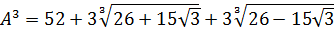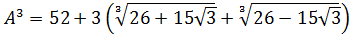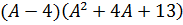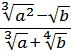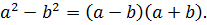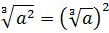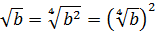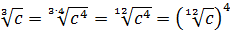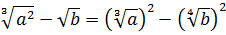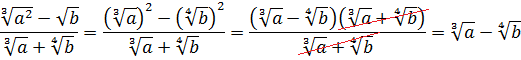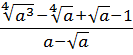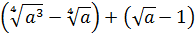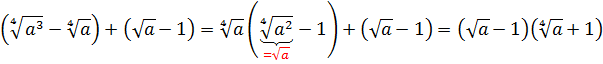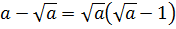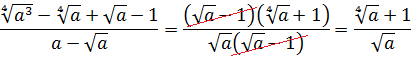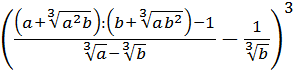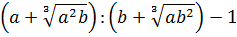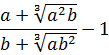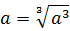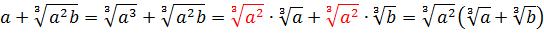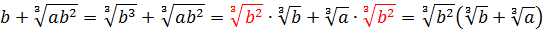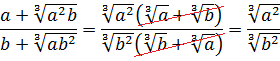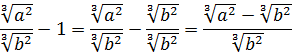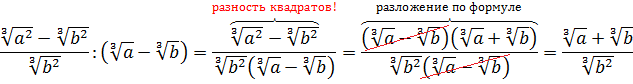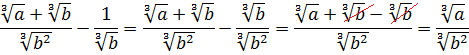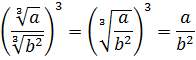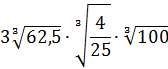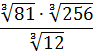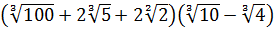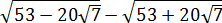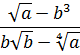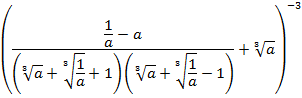Степени преобразование выражений содержащих степени решение иррациональных и показательных уравнений

Иррациональные выражения и их преобразования

В прошлый раз мы вспомнили (или узнали — кому как), что же такое корень n-й степени , научились извлекать такие корни, разобрали по винтикам основные свойства корней и решали несложные примеры с корнями.

Этот урок будет продолжением предыдущего и будет посвящён преобразованиям самых разных выражений, содержащих всевозможные корни. Такие выражения называются иррациональными. Здесь появятся и выражения с буквами, и дополнительные условия, и избавление от иррациональности в дробях, и некоторые продвинутые приёмы в работе с корнями. Те приёмы, которые будут рассматриваться в данном уроке, станут хорошей базой для решения задач ЕГЭ (и не только) практически любого уровня сложности. Итак, давайте приступим.

Прежде всего я продублирую здесь основные формулы и свойства корней. Чтобы не скакать из темы в тему. Вот они:

при

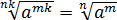
Формулы эти надо обязательно знать и уметь применять. Причём в обе стороны — как слева направо, так и справа налево. Именно на них и основывается решение большинства заданий с корнями любой степени сложности. Начнём пока с самого простого — с прямого применения формул или их комбинаций.

Простое применение формул

В этой части будут рассматриваться простые и безобидные примеры — без букв, дополнительных условий и прочих хитростей. Однако даже в них, как правило, имеются варианты. И чем навороченнее пример, тем больше таких вариантов. И у неопытного ученика возникает главная проблема — с чего начинать? Ответ здесь простой — не знаешь, что нужно — делай что можно. Лишь бы ваши действия шли в мире и согласии с правилами математики и не противоречили им.) Например, такое задание:

Вычислить:

Даже в таком простеньком примере возможны несколько путей к ответу.

Первый — просто перемножить корни по первому свойству и извлечь корень из результата:

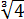
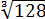
Второй вариант такой: не трогаем, работаем с . Выносим множитель из-под знака корня, а дальше — по первому свойству. Вот так:

Решать можно как больше нравится. В любом из вариантов ответ получается один — восьмёрка. Мне, например, проще перемножить 4 и 128 и получить 512, а из этого числа отлично извлекается кубический корень. Если кто-то не помнит, что 512 — это 8 в кубе, то не беда: можно записать 512 как 2 9 (первые 10 степеней двойки, я надеюсь, помните?) и по формуле корня из степени:

Вычислить: .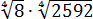

Если работать по первому свойству (всё загнать под один корень), то получится здоровенное число, из которого корень потом извлекать — тоже не сахар. Да и не факт, что он извлечётся ровно.) Поэтому здесь полезно в числе 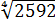вынести множители из-под корня. Причём вынести по максимуму:

И теперь всё наладилось:

Осталось восьмёрку и двойку записать под одним корнем (по первому свойству) и — готово дело. 🙂

Добавим теперь немного дробей.

Пример совсем примитивный, однако и в нём имеются варианты. Можно с помощью вынесения множителя преобразовать числитель и сократить со знаменателем:

А можно сразу воспользоваться формулой деления корней:

Как видим, и так, и сяк — всяко правильно.) Если не споткнуться на полпути и не ошибиться. Хотя где тут ошибаться-то…

Разберём теперь самый последний пример из домашнего задания прошлого урока:

Совершенно немыслимый набор корней, да ещё и вложенных. Как быть? Главное — не бояться! Здесь мы первым делом замечаем под корнями числа 2, 4 и 32 — степени двойки. Первое что нужно сделать — привести все числа к двойкам: всё-таки чем больше одинаковых чисел в примере и меньше разных, тем проще.) Начнём отдельно с первого множителя:

Число 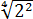можно упростить, сократив двойку под корнем с четвёркой в показателе корня:

Теперь, согласно корню из произведения:

.

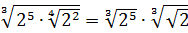
В числе 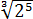выносим двойку за знак корня:

А с выражением 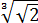расправляемся по формуле корня из корня:

Значит, первый множитель запишется вот так:

.

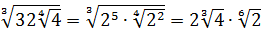
Вложенные корни исчезли, числа стали поменьше, что уже радует. Вот только корни разные, но пока так и оставим. Надо будет — преобразуем к одинаковым. Берёмся за второй множитель.)

Второй множитель преобразовываем аналогично, по формуле корня из произведения и корня из корня. Где надо — сокращаем показатели по пятой формуле:

Вставляем всё в исходный пример и получаем:

Получили произведение целой кучи совершенно разных корней. Неплохо было бы привести их все к одному показателю, а там — видно будет. Что ж, это вполне возможно. Наибольший из показателей корней равен 12, а все остальные — 2, 3, 4, 6 — делители числа 12. Поэтому будем приводить все корни по пятому свойству к одному показателю — к 12:

Считаем и получаем:

Красивого числа не получили, ну и ладно. Нас просили упростить выражение, а не посчитать. Упростили? Конечно! А вид ответа (целое число или нет) здесь уже не играет никакой роли.

Немного сложения / вычитания и формул сокращённого умножения

К сожалению, общих формул для сложения и вычитания корней в математике нету. Однако, в заданиях сплошь и рядом встречаются эти действия с корнями. Здесь необходимо понимать, что любые корни — это точно такие же математические значки, как и буквы в алгебре.) И к корням применимы те же самые приёмы и правила, что и к буквам — раскрытие скобок, приведение подобных, формулы сокращённого умножения и т.п.

Например, каждому ясно, что 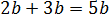. Точно так же одинаковые корни можно совершенно спокойно между собой складывать/вычитать:

Если корни разные, то ищем способ сделать их одинаковыми — внесением/вынесением множителя или же по пятому свойству. Если ну никак не упрощается, то, возможно, преобразования более хитрые.

Смотрим первый пример.

Найти значение выражения: .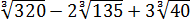

Все три корня хоть и кубические, но из разных чисел. Чисто не извлекаются и между собой складываются/вычитаются. Стало быть, применение общих формул здесь не катит. Как быть? А вынесем-ка множители в каждом корне. Хуже в любом случае не будет.) Тем более что других вариантов, собственно, и нету:

Стало быть, .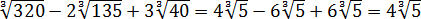

Вот и всё решение. Здесь мы от разных корней перешли к одинаковым с помощью вынесения множителя из-под корня. А затем просто привели подобные.) Решаем дальше.

Найти значение выражения:

С корнем из семнадцати точно ничего не поделаешь. Работаем по первому свойству — делаем из произведения двух корней один корень:

А теперь присмотримся повнимательнее. Что у нас под большим кубическим корнем? Разность ква.. Ну, конечно! Разность квадратов:

Теперь осталось только извлечь корень: .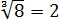

Дальше очень похожий пример, но посложнее.

Вычислить:

Здесь придётся проявить математическую смекалку.) Мыслим примерно следующим образом: «Так, в примере произведение корней. Под одним корнем разность, а под другим — сумма. Очень похоже на формулу разности квадратов. Но… Корни — разные! Первый квадратный, а второй — четвёртой степени… Хорошо бы сделать их одинаковыми. По пятому свойству можно легко из квадратного корня сделать корень четвёртой степени. Для этого достаточно подкоренное выражение возвести в квадрат.»

Если вы мыслили примерно так же, то вы — на полпути к успеху. Совершенно верно! Превратим первый множитель в корень четвёртой степени. Вот так:

Теперь, ничего не поделать, но придётся вспомнить формулу квадрата разности. Только в применении к корням. Ну и что? Чем корни хуже других чисел или выражений?! Возводим:

«Хм, ну возвели и что? Хрен редьки не слаще. Стоп! А если вынести четвёрку под корнем? Тогда выплывет то же самое выражение, что и под вторым корнем, только с минусом, а ведь именно этого мы и добиваемся!»

Верно! Выносим четвёрку:

.

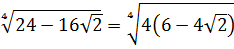
А теперь — дело техники:

.

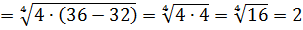
Вот так распутываются сложные примеры. ) Теперь пора потренироваться с дробями.

Ясно, что надо преобразовывать числитель. Как? По формуле квадрата суммы, разумеется. У нас есть ещё варианты разве? 🙂 Возводим в квадрат, выносим множители, сокращаем показатели (где надо):

Во как! Получили в точности знаменатель нашей дроби. ) Значит, вся дробь, очевидно, равна единице:

Ещё пример. Только теперь на другую формулу сокращённого умножения.)

Понятно, что квадрат разности надо в дело применять. Выписываем знаменатель отдельно и — поехали!

Выносим множители из-под корней:

Следовательно,

.

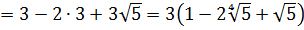
Теперь всё нехорошее великолепно сокращается и получается:

Что ж, поднимаемся на следующий уровень. 🙂

Буквы и дополнительные условия

Буквенные выражения с корнями — штука более хитрая, чем числовые выражения, и является неиссякаемым источником досадных и очень грубых ошибок. Перекроем этот источник.) Ошибки всплывают из-за того, что частенько таких заданиях фигурируют отрицательные числа и выражения. Они либо даны нам прямо в задании, либо спрятаны в буквах и дополнительных условиях. А нам в процессе работы с корнями постоянно надо помнить, что в корнях чётной степени как под самим корнем, так и в результате извлечения корня должно быть неотрицательное выражение. Ключевой формулой в задачах этого пункта будет четвёртая формула:

С корнями нечётной степени вопросов никаких — там всегда всё извлекается что с плюсом, что с минусом. И минус, если что, выносится вперёд. Будем сразу разбираться с корнями чётных степеней.) Например, такое коротенькое задание.

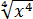
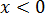
Упростить: , если .

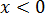
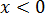
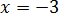
Казалось бы, всё просто. Получится просто икс. ) Но зачем же тогда дополнительное условие ? В таких случаях полезно прикинуть на числах. Чисто для себя.) Если , то икс — заведомо отрицательное число. Минус три, например. Или минус сорок. Пусть . Можно минус три возвести в четвёртую степень? Конечно! Получится 81. Можно из 81 извлечь корень четвёртой степени? А почему нет? Можно! Получится тройка. Теперь проанализируем всю нашу цепочку:

Что мы видим? На входе было отрицательное число, а на выходе — уже положительное. Было минус три, стало плюс три.) Возвращаемся к буквам. Вне всяких сомнений, по модулю это будет точно икс, но только сам икс у нас с минусом (по условию!), а результат извлечения (в силу арифметического корня!) должен быть с плюсом. Как получить плюс? Очень просто! Для этого достаточно перед заведомо отрицательным числом поставить минус.) И правильное решение выглядит так:

Кстати сказать, если бы мы воспользовались формулой 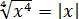, то, вспомнив определение модуля, сразу получили бы верный ответ. Поскольку

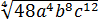
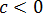
Вынести множитель за знак корня: , где .

Первый взгляд — на подкоренное выражение. Тут всё ОК. При любом раскладе оно будет неотрицательным. Начинаем извлекать. По формуле корня из произведения, извлекаем корень из каждого множителя:

Откуда взялись модули, объяснять, думаю, уже не надо.) А теперь анализируем каждый из модулей.

Множитель | a | так и оставляем без изменений: у нас нету никакого условия на букву a . Мы не знаем, положительное она или отрицательная. Следующий модуль | b 2 | можно смело опустить: в любом случае выражение b 2 неотрицательно. А вот насчёт | c 3 | — тут уже задачка.) Если 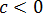, то и c 3 c 3 | = — c 3 . Итого верное решение будет такое:

А теперь — обратная задача. Не самая простая, сразу предупреждаю!

Внести множитель под знак корня: .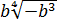

Если вы сразу запишете решение вот так

,

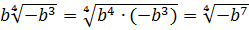
то вы попали в ловушку. Это неверное решение! В чём же дело?

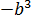
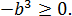
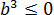
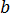
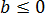
Давайте вглядимся в выражение под корнем . Под корнем четвёртой степени, как мы знаем, должно находиться неотрицательное выражение. Иначе корень смысла не имеет.) Поэтому А это, в свою очередь, значит, что и, следовательно, само также неположительно: .

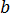
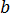
И ошибка здесь состоит в том, что мы вносим под корень неположительное число : четвёртая степень превращает его в неотрицательное и получается неверный результат — слева заведомый минус, а справа уже плюс. А вносить под корень чётной степени мы имеем право только неотрицательные числа или выражения. А минус, если есть, оставлять перед корнем.) Как же нам выделить неотрицательный множитель в числе , зная, что оно само стопудово отрицательное? Да точно так же! Поставить минус.) А чтобы ничего не поменялось, скомпенсировать его ещё одним минусом. Вот так:

И теперь уже неотрицательное число (-b) спокойно вносим под корень по всем правилам:

Этот пример наглядно показывает, что, в отличие от других разделов математики, в корнях правильный ответ далеко не всегда вытекает автоматически из формул. Необходимо подумать и лично принять верное решение.) Особенно следует быть внимательнее со знаками в иррациональных уравнениях и неравенствах.

Разбираемся со следующим важным приёмом в работе с корнями — избавлением от иррациональности.

Избавление от иррациональности в дробях

Если в выражении присутствуют корни, то, напомню, такое выражение называется выражением с иррациональностью. В некоторых случаях бывает полезно от этой самой иррациональности (т.е. корней) избавиться. Как можно ликвидировать корень? Корень у нас пропадает при… возведении в степень. С показателем либо равным показателю корня, либо кратным ему. Но, если мы возведём корень в степень (т.е. помножим корень сам на себя нужное число раз), то выражение от этого поменяется. Нехорошо.) Однако в математике бывают темы, где умножение вполне себе безболезненно. В дробях, к примеру. Согласно основному свойству дроби, если числитель и знаменатель умножить (разделить) на одно и то же число, то значение дроби не изменится.

Допустим, нам дана вот такая дробь:

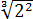
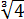
Можно ли избавиться от корня в знаменателе? Можно! Для этого корень надо возвести в куб. Чего нам не хватает в знаменателе для полного куба? Нам не хватает множителя , т.е. . Вот и домножаем числитель и знаменатель дроби на

Корень в знаменателе исчез. Но… он появился в числителе. Ничего не поделать, такова судьба.) Нам это уже не важно: нас просили знаменатель от корней освободить. Освободили? Безусловно.)

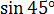
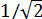
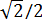
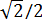
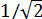
Кстати, те, кто уже в ладах с тригонометрией, возможно, обращали внимание на то, что в некоторых учебниках и таблицах, к примеру, обозначают по-разному: где-то , а где-то . Вопрос — что правильно? Ответ: всё правильно! ) Если догадаться, что – это просто результат освобождения от иррациональности в знаменателе дроби . 🙂

Зачем нам освобождаться от иррациональности в дробях? Какая разница — в числителе корень сидит или в знаменателе? Калькулятор всё равно всё посчитает.) Ну, для тех, кто не расстаётся с калькулятором, разницы действительно практически никакой… Но, даже считая на калькуляторе, можно обратить внимание на то, что делить на целое число всегда удобнее и быстрее, чем на иррациональное. А уж про деление в столбик вообще умолчу.)

Следующий пример только подтвердит мои слова.

Освободиться от иррациональности в знаменателе дроби:

Как здесь ликвидировать квадратный корень в знаменателе? Если числитель и знаменатель помножить на выражение 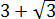, то в знаменателе получится квадрат суммы. Сумма квадратов первого и второго чисел дадут нам просто числа безо всяких корней, что очень радует. Однако… всплывёт удвоенное произведение первого числа на второе, где корень из трёх всё равно останется. Не канает. Как быть? Вспомнить другую замечательную формулу сокращённого умножения! Где никаких удвоенных произведений, а только квадраты:

Такое выражение, которое при домножении какой-то суммы (или разности) выводит на разность квадратов, ещё называют сопряжённым выражением. В нашем примере сопряжённым выражением будет служить разность 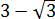. Вот и домножаем на эту разность числитель и знаменатель:

Что тут можно сказать? В результате наших манипуляций не то что корень из знаменателя исчез — вообще дробь исчезла! 🙂 Даже с калькулятором отнять корень из трёх от тройки проще, чем считать дробь с корнем в знаменателе. Ещё пример.

Освободиться от иррациональности в знаменателе дроби:

Как здесь выкручиваться? Формулы сокращённого умножения с квадратами сразу не катят — не получится полной ликвидации корней из-за того, что корень у нас в этот раз не квадратный, а кубический. Надо, чтобы корень как-то возвёлся в куб. Стало быть, применять надо какую-то из формул с кубами. Какую? Давайте подумаем. В знаменателе — сумма 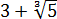. Как нам добиться возведения корня в куб? Домножить на неполный квадрат разности! Значит, применять будем формулу суммы кубов. Вот эту:

В качестве a у нас тройка, а в качестве b — корень кубический из пяти:

И снова дробь исчезла.) Такие ситуации, когда при освобождении от иррациональности в знаменателе дроби у нас вместе с корнями полностью исчезает сама дробь, встречаются очень часто. Как вам вот такой примерчик!

Попробуйте просто сложить эти три дроби! Без ошибок! 🙂 Один общий знаменатель чего стоит. А что, если попробовать освободиться от иррациональности в знаменателе каждой дроби? Что ж, пробуем:

Ух ты, как интересно! Все дроби пропали! Напрочь. И теперь пример решается в два счёта:

Просто и элегантно. И без долгих и утомительных вычислений. 🙂

Именно поэтому операцию освобождения от иррациональности в дробях надо уметь делать. В подобных навороченных примерах только она и спасает, да.) Разумеется, внимательность никто не отменял. Бывают задания, где просят избавиться от иррациональности в числителе. Эти задания ничем от рассмотренных не отличаются, только от корней очищается числитель.)

Более сложные примеры

Осталось рассмотреть некоторые специальные приёмы в работе с корнями и потренироваться распутывать не самые простые примеры. И тогда полученной информации уже будет достаточно для решения заданий с корнями любого уровня сложности. Итак — вперёд.) Для начала разберёмся, что делать со вложенными корнями, когда формула корня из корня не работает. Например, вот такой примерчик.

Вычислить:

Корень под корнем… К тому же под корнями сумма или разность. Стало быть, формула корня из корня (с перемножением показателей) здесь не действует. Значит, надо что-то делать с подкоренными выражениями: у нас просто нету других вариантов. В таких примерах чаще всего под большим корнем зашифрован полный квадрат какой-нибудь суммы. Или разности. А корень из квадрата уже отлично извлекается! И теперь наша задача — его расшифровать.) Такая расшифровка красиво делается через систему уравнений. Сейчас всё сами увидите.)

Итак, под первым корнем у нас вот такое выражение:

А вдруг, не угадали? Проверим! Возводим в квадрат по формуле квадрата суммы:

Всё верно.) Но… Откуда я взял это выражение 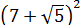? С неба?

Нет.) Мы его чуть ниже получим честно. Просто по данному выражению я показываю, как именно составители заданий шифруют такие квадраты. 🙂 Что такое 54? Это сумма квадратов первого и второго чисел. Причём, обратите внимание, уже без корней! А корень остаётся в удвоенном произведении, которое в нашем случае равно 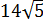. Поэтому распутывание подобных примеров начинается с поиска удвоенного произведения. Если распутывать обычным подбором. И, кстати, о знаках. Тут всё просто. Если перед удвоенным плюс, то квадрат суммы. Если минус, то разности.) У нас плюс — значит, квадрат суммы.) А теперь — обещанный аналитический способ расшифровки. Через систему.)

Итак, у нас под корнем явно тусуется выражение (a+b) 2 , и наша задача — найти a и b. В нашем случае сумма квадратов даёт 54. Вот и пишем:

Теперь удвоенное произведение. Оно у нас 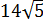. Так и записываем:

Получили вот такую системку:

Решаем обычным методом подстановки. Выражаем из второго уравнения, например, и подставляем в первое:

Решим первое уравнение:

Получили биквадратное уравнение относительно a . Считаем дискриминант:

Получили аж четыре возможных значения a . Не пугаемся. Сейчас мы всё лишнее отсеем.) Если мы сейчас для каждого из четырёх найденных значений посчитаем соответствующие значения , то получим четыре решения нашей системы. Вот они:

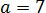
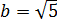
И тут вопрос — а какое из решений нам подходит? Давайте подумаем. Отрицательные решения можно сразу отбросить: при возведении в квадрат минусы «сгорят», и всё подкоренное выражение в целом не изменится.) Остаются первые два варианта. Выбрать их можно совершенно произвольно: от перестановки слагаемых сумма всё равно не меняется.) Пусть, например, , а .

Итого получили под корнем квадрат вот такой суммы:

Я не зря так детально описываю ход решения. Чтобы было понятно, как происходит расшифровка.) Но есть одна проблемка. Аналитический способ расшифровки хоть и надёжный, но весьма длинный и громоздкий: приходится решать биквадратное уравнение, получать четыре решения системы и потом ещё думать, какие из них выбрать… Хлопотно? Согласен, хлопотно. Этот способ безотказно работает в большинстве подобных примеров. Однако очень часто можно здорово сократить себе работу и найти оба числа творчески. Подбором.) Да-да! Сейчас, на примере второго слагаемого (второго корня), я покажу более лёгкий и быстрый способ выделения полного квадрата под корнем.

Итак, теперь у нас вот такой корень: .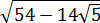

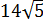
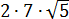
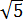
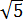
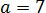
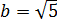
Размышляем так: «Под корнем — скорее всего, зашифрованный полный квадрат. Раз перед удвоенным минус — значит, квадрат разности. Сумма квадратов первого и второго чисел даёт нам число 54 . Но какие это квадраты? 1 и 53 ? 49 и 5 ? Слишком много вариантов… Нет, лучше начать распутывать с удвоенного произведения. Наши можно расписать как . Раз произведение удвоенное, то двойку сразу отметаем. Тогда кандидатами на роль a и b остаются 7 и . А вдруг, это 14 и /2 ? Не исключено. Но начинаем-то всегда с простого!» Итак, пусть , а . Проверим их на сумму квадратов:

Получилось! Значит, наше подкоренное выражение — это на самом деле квадрат разности:

Вот такой вот способ-лайт, чтобы не связываться с системой. Не всегда работает, но во многих таких примерах его вполне достаточно. Итак, под корнями — полные квадраты. Осталось только правильно извлечь корни, да досчитать пример:

А теперь разберём ещё более нестандартное задание на корни.)

Докажите, что число A – целое, если .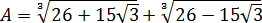

Впрямую ничего не извлекается, корни вложенные, да ещё и разных степеней… Кошмар! Однако, задание имеет смысл.) Стало быть, ключ к его решению имеется.) А ключ здесь такой. Рассмотрим наше равенство

как уравнение относительно A. Да-да! Хорошо бы избавиться от корней. Корни у нас кубические, поэтому возведём-ка обе части равенства в куб. По формуле куба суммы:

Кубы и корни кубические друг друга компенсируют, а под каждым большим корнем забираем одну скобку у квадрата и сворачиваем произведение разности и суммы в разность квадратов:

Отдельно сосчитаем разность квадратов под корнями:

Отлично! Значит, всё наше равенство ещё сильнее упростится:

А теперь делаем финт ушами — заменяем сумму корней в скобках на A (согласно условию примера!).

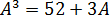
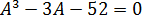
Получаем кубическое уравнение или .

Здесь как раз тот случай, когда один из корней легко угадывается — это 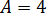. Значит, наш многочлен можно разложить как

Как разложить? Либо по схеме Горнера, либо делением «уголком» на скобку (A-4), либо даже группировкой (если представить -3A как -16A+13A). Объяснять подробно деление уголком или схему Горнера в теме про корни — уже совсем отклоняться от курса.) Кто в теме — и так поймёт.

А теперь легко заметить, что квадратный трёхчлен во вторых скобках имеет отрицательный дискриминант, а значит, наше уравнение имеет единственный действительный корень 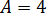. И поэтому наша страшная сумма корней в действительности равна просто 4. То есть, явно целому числу. Что и требовалось доказать.)

А теперь — поупрощаем некоторые дробные выражения с корнями. От простого — к сложному. Здесь всё точно так же, как и с многочленами. Только в применении к корням.) Я же говорил, что действия с корнями ничем не отличаются от таковых с буквами. И к корням с таким же успехом применима вся алгебра седьмого класса — формулы сокращённого умножения, разложение на множители, приведение подобных и т.п.

Например, такое задание.

Пример явно намекает на применение формулы разности квадратов:

Спрашивается, а где же здесь квадраты? Сплошные корни… Сейчас покажу. 🙂

Берём числитель нашей дробушки: .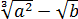

Что такое 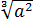? По свойству корня из степени, мы можем вынести квадрат наружу. Вот так:

Хорошо, а из 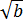как квадрат сделать? Не вопрос! По пятому свойству, домножаем на двойку показатели корня и подкоренного выражения:

По такой технологии, между прочим, можно совершенно любой корень превратить в совершенно любую степень. Какую хотим. 🙂 Как, например, 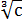представить в виде 4-й степени? Нет проблем:

Хотим из степеней корни делаем, хотим — наоборот, степени из корней. Что хотим, то и творим. Математика, однако! 🙂

Итак, весь наш числитель можно представить как разность квадратов:

А дальше никаких проблем — раскладываем числитель на множители и сокращаем:

Действуем аналогично. Раскладываем на множители и сокращаем. 🙂 В числителе применяем группировку. Например, вот такую:

А в знаменателе просто выносим общий множитель :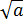

Подставляем всё в нашу дробь и сокращаем:

Как видим, разложение на множители очень популярно в теме с корнями. Очень! И особенно — формула разности квадратов. Именно поэтому формулы сокращённого умножения так важно знать и уметь применять. 🙂

Ну и на десерт распутаем что-нибудь навороченное. )

Чтобы не запутаться и не наляпать ошибок, будем действовать по порядку. При взгляде на любой пример всегда задаём сами себе вопрос: «Что в примере мне больше всего не нравится?» В данном примере большинство скажет: «Числитель первой дроби!» Верно! Вот и упростим его отдельно: остальная часть примера от этого никак не пострадает.) Итак,

Вместо знака деления удобно использовать черту дроби. Вот так:

Сначала упростим дробь. Как? Попробуем сократить.) Для этого, ясное дело, надо разложить на множители числитель и знаменатель, да… Берём отдельно числитель 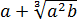. Можно его разложить на множители? Можно! Для этого из a надо сделать корень. Вот так:

Если теперь подставить вместо a выражение 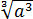, то всплывёт общий множитель. 🙂

Со знаменателем полная аналогия:

Теперь от упрощённой дроби отнимаем единичку. Как? Делаем из единички дробь и — вперёд!

Следующим пунктом идёт деление полученной дроби на выражение 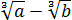. Это означает, что оно пойдёт у нас в знаменатель:

Уфф… Дальше… Отнимаем от полученного выражения дробь :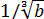

И, наконец, последнее усилие. Возводим результат в куб:

Ну как, всё понятно? Тогда — вперёд, набиваем руку и делаем примеры!

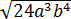
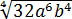
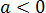
Вынести множители за знак корня: , , где .

Внести множители под знак корня: , .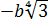

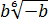
Освободиться от иррациональности в знаменателе дробей:

, .

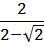
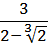
Вычислить:

Доказать, что A – целое число, если .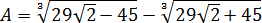

Ответы (пока) давать не буду — иначе неинтересно. 🙂 До встречи и успехов!

Видео:Показательные уравнения. 11 класс.Скачать

Степенные выражения (выражения со степенями) и их преобразование

Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Что представляют собой степенные выражения?

В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.

Степенное выражение – это выражение, которое содержит степени.

Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.

Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , ( 2 + 1 ) 5 , ( − 0 , 1 ) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , ( a 2 ) 3 . А также степени с нулевым показателем: 5 0 , ( a + 1 ) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: ( 0 , 5 ) 2 + ( 0 , 5 ) — 2 2 .

Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 — 3 · 3 · 3 1 2 , 2 3 , 5 · 2 — 2 2 — 1 , 5 , 1 a 1 4 · a 1 2 — 2 · a — 1 6 · b 1 2 , x π · x 1 — π , 2 3 3 + 5 .

В качестве показателя может выступать переменная 3 x — 54 — 7 · 3 x — 58 или логарифм x 2 · l g x − 5 · x l g x .

С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Основные виды преобразований степенных выражений

В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.

Вычислите значение степенного выражения 2 3 · ( 4 2 − 12 ) .

Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · ( 4 2 − 12 ) = 2 3 · ( 16 − 12 ) = 2 3 · 4 .

Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.

Ответ: 2 3 · ( 4 2 − 12 ) = 32 .

Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .

Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .

Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .

Представьте выражение со степенями 9 — b 3 · π — 1 2 в виде произведения.

Решение

Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:

9 — b 3 · π — 1 2 = 3 2 — b 3 · π — 1 2 = = 3 — b 3 · π — 1 3 + b 3 · π — 1

Ответ: 9 — b 3 · π — 1 2 = 3 — b 3 · π — 1 3 + b 3 · π — 1 .

А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.

Видео:Степень числа с рациональным показателем. 11 класс.Скачать

Работа с основанием и показателем степени

Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 и ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.

Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.

Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) и получить степенное выражение более простого вида a 2 · ( x + 1 ) .

Видео:Преобразование иррациональных выражений. 11 класс.Скачать

Использование свойств степеней

Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:

• a r · a s = a r + s ;
• a r : a s = a r − s ;
• ( a · b ) r = a r · b r ;
• ( a : b ) r = a r : b r ;
• ( a r ) s = a r · s .

В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .

Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.

При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».

Представьте выражение a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 в виде степени с основанием a .

Решение

Для начала используем свойство возведения в степень и преобразуем по нему второй множитель ( a 2 ) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:

a 2 , 5 · a − 6 : a − 5 , 5 = a 2 , 5 − 6 : a − 5 , 5 = a − 3 , 5 : a − 5 , 5 = a − 3 , 5 − ( − 5 , 5 ) = a 2 .

Ответ: a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 = a 2 .

Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.

Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .

Решение

Если мы применим равенство ( a · b ) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .

Есть еще один способ провести преобразования:

3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · ( 3 · 7 ) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21

Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21

Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .

Решение

Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени ( a r ) s = a r · s справа налево и получим ( a 0 , 5 ) 3 : a 1 , 5 − a 0 , 5 − 6 = ( a 0 , 5 ) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .

Ответ: t 3 − t − 6 .

Видео:Преобразование выражений, содержащих степени с рациональными показателями 1Скачать

Преобразование дробей, содержащих степени

Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.

Упростить степенное выражение 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 .

Решение

Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:

3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = 3 · 5 2 3 · 5 1 3 — 3 · 5 2 3 · 5 — 2 3 — 2 — x 2 = = 3 · 5 2 3 + 1 3 — 3 · 5 2 3 + — 2 3 — 2 — x 2 = 3 · 5 1 — 3 · 5 0 — 2 — x 2

Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 — 2 — x 2 = — 12 2 + x 2

Ответ: 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = — 12 2 + x 2

Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.

Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .

Решение

а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.

Выполним умножение числителя и знаменателя дроби на a 0 , 3 :

a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a

б) Обратим внимание на знаменатель:

x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 — x 1 3 · 2 · y 1 6 + 2 · y 1 6 2

Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т.е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.

Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x и y выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2

Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .

Сократите дробь: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 , б) a 1 4 — b 1 4 a 1 2 — b 1 2 .

Решение

а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .

30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 )

б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:

a 1 4 — b 1 4 a 1 2 — b 1 2 = a 1 4 — b 1 4 a 1 4 2 — b 1 2 2 = = a 1 4 — b 1 4 a 1 4 + b 1 4 · a 1 4 — b 1 4 = 1 a 1 4 + b 1 4

Ответ: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 ) , б) a 1 4 — b 1 4 a 1 2 — b 1 2 = 1 a 1 4 + b 1 4 .

К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.

Выполните действия x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 .

Решение

Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:

x 1 2 — 1 · x 1 2 + 1

x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 — x 1 2 — 1 · x 1 2 — 1 x 1 2 + 1 · x 1 2 — 1 · 1 x 1 2 = = x 1 2 + 1 2 — x 1 2 — 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 — x 1 2 2 — 2 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2

Теперь умножаем дроби:

4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · x 1 2

Произведем сокращение на степень x 1 2 , получим 4 x 1 2 — 1 · x 1 2 + 1 .

Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 — 1 · x 1 2 + 1 = 4 x 1 2 2 — 1 2 = 4 x — 1 .

Ответ: x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = 4 x — 1

Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 .
Решение

Мы можем произвести сокращение дроби на ( x 2 , 7 + 1 ) 2 . Получаем дробь x 3 4 x — 5 8 · x 2 , 7 + 1 .

Продолжим преобразования степеней икса x 3 4 x — 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x — 5 8 · 1 x 2 , 7 + 1 = x 3 4 — — 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .

Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .

Ответ: x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .

Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение ( x + 1 ) — 0 , 2 3 · x — 1 можно заменить на x 3 · ( x + 1 ) 0 , 2 .

Видео:Преобразование выражений, содержащих кв.корни. Внесение и вынесения из, под знак кв. корня. 8 класс.Скачать

Преобразование выражений с корнями и степенями

В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.

Представьте выражение x 1 9 · x · x 3 6 в виде степени.

Решение

Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞ ) .

На этом множестве мы имеем право перейти от корней к степеням:

x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6

Используя свойства степеней, упростим полученное степенное выражение.

x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3

Ответ: x 1 9 · x · x 3 6 = x 1 3 .

Видео:Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать

Преобразование степеней с переменными в показателе

Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .

Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:

5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .

Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:

5 · 5 — 3 · 5 x · 7 x — 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 2 · x — 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 x · 7 x — 2 · 7 2 · x 7 2 · x = 0

Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x — 3 · 5 x 7 x — 2 = 0 .

Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x — 3 · 5 7 x — 2 = 0 , которое равносильно 5 · 5 7 x 2 — 3 · 5 7 x — 2 = 0 .

Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .

Видео:Преобразование выражений, содержащих степени. 7 классСкачать

Преобразование выражений со степенями и логарифмами

Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 — 5 · log 2 3 или log 3 27 9 + 5 ( 1 — log 3 5 ) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».

Видео:Как решать Показательные Уравнения? (часть 2)Скачать

Конспект лекций (раздаточный материал) по учебной дисциплине «Математика: Алгебра» по разделу » Иррациональные уравнения. Показательные уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Конспект лекции Иррациональные, показательные уравнения.docx

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ВОЛЖСКИЙ ИНСТИТУТ ЭКОНОМИКИ, ПЕДАГОГИКИ И ПРАВА»

Волжский социально-педагогический колледж

Математика: Алгебра (10-11кл., 1 курс СПО)

Конспект лекций (раздаточный материал) по разделу

«Иррациональные уравнения. Показательные уравнения»

Автор: Бондаренко Людмила Валентиновна

Место работы: Волжский социально-педагогический колледж – структурное подразделение ВИЭПП

Иррациональными называются уравнения, в которых переменная содержится под знаком корня.

Чаще всего иррациональное уравнение можно решить, если преобразовать его в рациональное уравнение. Для того чтобы избавиться от иррациональности, обычно обе части уравнения возводят в одну и ту же степень . При этом учитываются правила:

При возведении в не четную степень всегда получаем уравнение, равносильное заданному (на его ОДЗ). Все корни равносильного уравнения являются корнями заданного . И наоборот, все корни заданного уравнения являются корнями равносильного уравнения.

При возведении в четную степень получаем уравнение-следствие. В этом случае все корни заданного уравнения будут корнями уравнения-следствия , а обратное условие не выполняется. Не все корни уравнения- следствия будут корнями заданного. Чтобы определить, являются ли корни уравнения-следствия корнями заданного уравнения, надо проверить все полученные корни.

Это свойство связано с тем, что одно и то же число может быть получено возведением в четную степень двух противоположных чисел.

Т.о., если корень четной степени необходимо искать ОДЗ, либо сделать проверку.

Какие из данных уравнений не имеют корней

Примеры решения иррациональных уравнений

Пример 1 . Решим уравнение

Возведем обе части уравнения в третью степень. Получим равносильное уравнение:

Перенесем все слагаемые в одну сторону и вынесем за скобки х:

Приравняем каждый множитель к нулю, получим:

, ,

Пример 2 . Решим уравнение:

Перейдем к равносильной системе:

Решим первое уравнение системы и проверим, какие корни удовлетворяют неравенству.

Неравенству удовлетворяет только корень Ответ: x=1

Показательная функция, ее свойства и график.

Рис 36.

№ 204

Уравнения, которые содержат переменную в показателе степени , называют показательными уравнениями . Например: 2 х = 8, 9 х -6· 3 + 6= 0, 0,6 (х -3) = 3

Уравнения вида а х = а b , где а 0, а 1 называются простейшими показательными уравнениями.
Простейшие показательные уравнения решаются с использованием свойств степени: степени с одинаковым основанием а 0, а 1 равны тогда и только тогда, когда равны их показатели.

если а х = а b , то х = b , т.е. в общем виде

Метод приведения степеней к одному основанию .

Методика решения простейших показательных уравнений: 1 . Приводим к одному основанию степени; 2 . Приравниваем показатели степени; 3 . Решаем полученное уравнение.

Но 1 = ( 2 / ₃ ) 0 , поэтому х = 0. Проверка показывает, что это действительно корень данного уравнения. Ответ , х = 0.

Вынесение общего множителя за скобки .

Пример : 3 2х+2 + 5 · 3 2х-2 = 86. Вынесем выражение, содержащее наименьший показатель степени за скобки. Для того, чтобы вынести за скобку, надо разделить каждое слагаемое на 3 2х-2 ,получим

Использование замены переменной.

2 2х + 2·2 х -80 = 0. Производим замену переменной, обозначим 2 х = у, тогда 2 2х = у 2 . Перепишем наше уравнение. у 2 + 2у — 80 = 0. Получили обычное квадратное уравнение, решаем его:

D = 4 — 4· (-80) = 324. у = . у = — 10; у = 8. Т.к. 2 х 0, то у = — 10 мы отсеиваем (показательная функция не может принимать отрицательные значения), т.е. у = 8

Произведем обратную замену 2 х = 8 2 х = 2 3 х =3

Рассмотрим методику решения показательных неравенств . Все они в большинстве случаев сводятся к такому типу :

Методика решения подобных неравенств основана на монотонном возрастании показательной функции, когда основание степени больше единицы: 1 . Уравнять основания степеней;

2 . Сравнить показатели, сохранив знак неравенства ; 3 . Решить полученное неравенство;

Методика решения подобных неравенств основана на монотонном убывании показательной функции, когда основание степени лежит в пределах от нуля до единицы : 1 . Уравнять основания степеней; 2 . Сравнить показатели, изменив знак неравенства ; 3 . Решить полученное неравенство;

💥 Видео

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

10 класс. Алгебра. Преобразование выражений, содержащих степени.Скачать

Преобразование выражений, содержащих квадратные корни. Избавление от иррациональности. 8 класс.Скачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Преобразование выражений, содержащих кв.корни. Внесение и вынесения из, под знак кв. корня. 8 класс.Скачать

11 класс, 7 урок, Преобразование выражений содержащих радикалыСкачать

Преобразование выражений, содержащих радикалы | Алгебра 11 класс #4 | ИнфоурокСкачать

Преобразование иррациональных выражений. Практическая часть. 11 класс.Скачать

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ😩 #математика #shorts #егэ #огэ #уравнение #показательныеуравненияСкачать

СТЕПЕНИ с рациональным показателям СТЕПЕНИ с действительным показателямСкачать