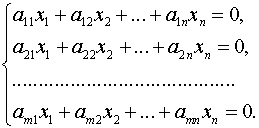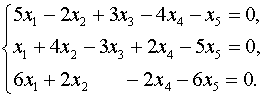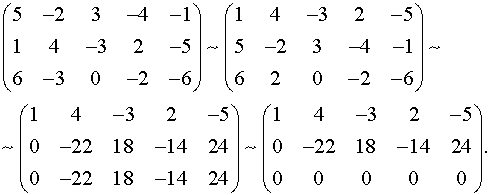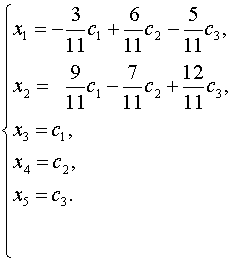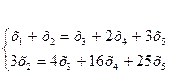Установить размерность пространства решений однородной системы уравнений указать базис (2 видео)

Решебник.Ру / Кузнецов Л.А. Линейная алгебра. Задача 3

Содержание

Системы линейных однородных уравнений
21. Пространство решений системы линейных однородных уравнений
Разберите решение задачи 3
📽️ Видео

Системы линейных однородных уравнений

Постановка задачи. Найти какой-нибудь базис и определить размерность линейного пространства решений системы

1. Записываем матрицу системы:

и с помощью элементарных преобразований преобразуем матрицу к треугольному виду, т.е. к такому виду, когда все элементы, находящиеся ниже главной диагонали равны нулю. Ранг матрицы системы равен числу линейно независимых строк, т.е., в нашем случае, числу строк, в которых остались ненулевые элементы:

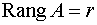
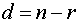
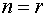
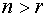
Размерность пространства решений равна . Если , то однородная система имеет единственное нулевое решение, если , то система имеет бесчисленное множество решений.

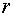
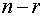
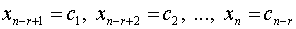
2. Выбираем базисных и свободных переменных. Свободные переменные обозначаем . Затем базисные переменные выражаем через свободные, получив таким образом общее решение однородной системы линейных уравнений.

3. Записываем базис пространства решений системы полагая последовательно одну из свободных переменных равной единице, а остальные нулю. Размерность линейного пространства решений системы равна количеству векторов базиса.

Примечание. К элементарным преобразованиям матрицы относят:

1. умножение (деление) строки на множитель, отличный от нуля;

2. прибавление к какой-либо строке другой строки, умноженной на любое число;

3. перестановка строк местами;

4. преобразования 1–3 для столбцов (в случае решения систем линейных уравнений элементарные преобразования столбцов не используются).

Задача 3. Найти какой-нибудь базис и определить размерность линейного пространства решений системы.

Выписываем матрицу системы и с помощью элементарных преобразований приводим ее к треугольному виду:

Полагаем , тогда

Размерность линейного пространства решений равна 3.

:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

21. Пространство решений системы линейных однородных уравнений

Пусть дана система (30) линейных однородных уравнений с коэффициентами из поля Р.

(30)

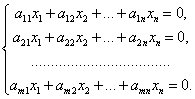
Так как столбец свободных членов в матрице А1 этой системы состоит только из нулей, то rang A = rang A1, т. е. система линейных однородных уравнений всегда совместна. В частности она всегда имеет нулевое решение. Рассмотрим множество всех возможных решений системы (30).

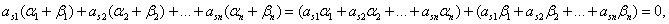
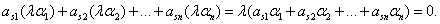
Пусть A =(A1, A2, … , An) и B =(B1, B2, … , Bn) – Любые два из них. Их можно рассматривать, как векторы в арифметическом n-мерном пространстве над полем Р. Пусть L – любой элемент поля Р. Тогда A +B = (A1 + B1, A2 + B2, … , An + Bn ), L×A = (LA1, LA2, … , LAn). Подставим компоненты этих векторов в произвольное S-е уравнение системы (30). Получим Итак, если A и B – Любые два решения системы (30) и L – любой элемент поля Р, то A +B И L×A тоже являются решением этой системы. Но тогда из теоремы 14 следует

Теорема 27. Множество решений системы линейных однородных уравнений с N Переменными есть линейное подпространство арифметического пространства Аn .

Теорема 28. Размерность пространства решений системы линейных однородных уравнений равна N – r, Где N – Число неизвестных, r – ранг матрицы системы.

Доказательство. Пусть L – пространство решений системы (30). Тогда L Ì Аn . Пусть A = (A1, A2, … Ar, Ar+1, … , An) – произвольное решение системы. Пусть (Ar+1, … , An) – набор свободных неизвестных, соответствующий этому решению. Множество всех возможных наборов свободных неизвестных есть арифметическое (N – r)-мерное пространство Аn–r . Зададим отображение J: L ® Аn–r по правилу

Покажем, что J – изоморфизм (определение 24). Для этого нужно проверить три условия.

1. Покажем, что J – взаимнооднозначное отображение. Решению A = (A1, A2, … Ar, Ar+1, … , An) соответствует только один набор (Ar+1, … , An), следовательно, J – Однозначное отображение. Обратно, если задать элемент (Ar+1, … , An) из Аn–r , то по теореме Крамера найдётся только один набор (A1, A2, … Ar ) искомых неизвестных, т. е. каждый элемент J(A) из Аn–r соответствует единственному элементу из L .

Итак, пространство решений системы линейных однородных уравнений изоморфно арифметическому (N – r)-мерному пространству. Следовательно, размерность L равна (N – r).

Определение 29. Базис пространства решений системы линейных однородных уравнений называется её Фундаментальной системой решений.

Так как при изоморфизме базис пространства Аn–r соответствует базису пространства L , То для того. чтобы найти фундаментальную систему решений для системы (30), достаточно выбрать (N – r) линейно независимых наборов свободных неизвестных и для каждого из них найти решение данной системы.

Следствие. Если А1, а2, …, аN–r фундаментальная система решений системы линейных однородных уравнений (30) и С1, С2, … , СN–r – произвольные элементы поля Р, то С1А1 + С2А2 + … + СN–r АN–r – общее решение этой системы.

Видео:Базис линейного пространства (01)Скачать

Разберите решение задачи 3

Найти общее решение однородной системы линейных уравнений и проанализировать его структуру (указать базис пространства решений однородной системы, установить размерность пространства):

Решение:

Множество решений однородной СЛАУ является подпространством линейного пространства и обозначается (ker A). Размерность этого подпространства определяют по формуле: dim(ker A) = n – r, где n – количество неизвестных в однородной СЛАУ, r – ранг матрицы А. В нашем случае n =5. Необходимо найти ранг матрицы. Запишем матрицу коэффициентов СЛАУ и найдем ее ранг методом элементарных преобразований:

1) поменяем местами строки;

2) от элементов 2-ой строки вычтем элементы 1-ой строки, умноженной на 6; от элементов 3-ей строки вычтем элементы 1-ой строки, умноженной на 7;

3) от элементов 3-ей строки вычитаем элементы 2-ой, получаем нулевую строку и вычеркиваем ее

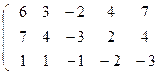
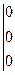
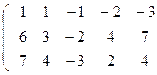
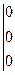
Ранг матрицы А равен числу ненулевых строк. Таким образом, r=2.

dim(ker A) = n – r=5-2=3. Т.е., линейное подпространство решений данной однородной СЛАУ имеет размерность 3. Следовательно, имеется три линейно независимых решения, которые образуют фундаментальную систему решений (ФСР) данной однородной СЛАУ. Решим укороченную систему:

Выберем в качестве базисного минора 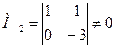, также ранг полученной расширенной матрицы равен 2, тогда выберем два базисных неизвестных, например, х₁ и х₂. Оставшиеся х₃, х₄, х₅ будут свободными неизвестными. В укороченной системе базисные неизвестные перенесем в левую часть, а свободные неизвестные – в правую часть равенств.

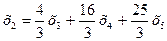
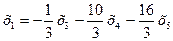
Из последнего уравнения находим .Подставляя найденное значение х₂ в первое уравнение, найдем х₁:

Базисные решения получим, если свободным неизвестным будем придавать поочередно значение 1, полагая остальные равными 0.

При х₃=1, х₄=0, х₅=0, получим .

При х₃=0, х₄=1, х₅=0, получим .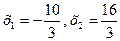

При х₃=0, х₄=0, х₅=1, получим .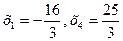

Запишем базис линейного пространства решений однородной СЛАУ –

фундаментальную систему решений:

, , .

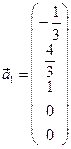
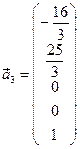
Размерность линейного пространства решений однородной СЛАУ равна 3.

Базис: .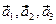

Вопросы для самопроверки

1. Напишите формулы Крамера решения системы линейных

уравнений. В каких случаях система уравнений имеет а) единственное решение; б)бесчисленное множество решений; в)не имеет решения. В каких случаях можно использовать формулы Крамера.

1. Объясните схему решения системы линейных уравнений по

2. Какая матрица называется обратной по отношению к данной

матрице? Напишите формулу обратной матрицы.