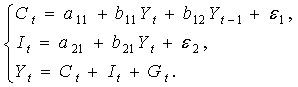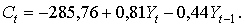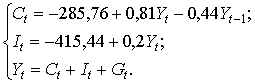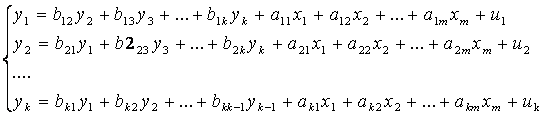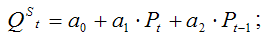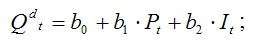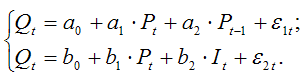Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.
Введем следующие обозначения:
М – число предопределенных переменных в модели;
m— число предопределенных переменных в данном уравнении;
— число эндогенных переменных в модели;
— число эндогенных переменных в данном уравнении;
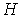
Обозначим число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение через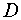 
, 
.
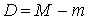
Тогда условие идентифицируемости каждого уравнения модели может быть записано в виде следующего счетного правила:
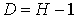 | уравнение идентифицируемо |
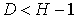 | уравнение неидентифицируемо |
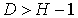 | уравнение сверхидентифицируемо |
Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.
Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации.
Достаточное условие идентификации
Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.
Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но не достаточное условие идентификации.
В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны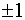 
. В этом случае, хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при переменных в тождестве известны, в проверке на идентификацию структурных уравнений системы тождества участвуют..
Изучается модель (одна из версий модели Кейнса):
(7.8)
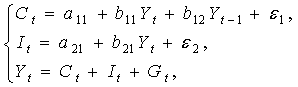
где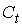 
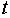
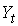
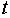
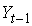
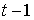
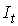
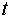
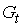
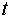
– потребление в период 
; 
– ВВП в период ; 
— ВВП в период ( 
); 
– валовые инвестиции в период 
; 
– государственные расходы в период .
Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение –тождество ВВП. Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные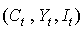 
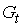
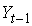
и две предопределенные переменные (одна экзогенная переменная – и одна лаговая переменная – ).
Проверим необходимое условие идентификации для каждого из уравнений модели.
| N | Уравнение | 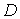 | счетное правило |
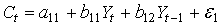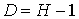 |  | идентифицируемо | |
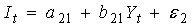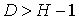 |  | сверхидентифицируемо | |
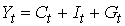 | тождество, не подлежит проверке |
Например, первое уравнение содержит две эндогенные переменные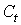 
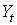
и 
и одну предопределенную переменную 
.
Таким образом,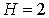 
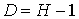
; D=2-1=1. Условие условие выполняется, т. е. уравнение идентифицируемо.
Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.
| | | |  | | |
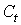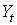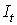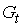| I уравнение | -1 | b11 | b12 | 0 | 0 |
| II уравнение | 0 | b21 | 0 | -1 | 0 |
| Тождество | 1 | 0 | 0 | 1 | 1 |
В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного.
Первое уравнение: матрица коэффициентов при переменных, не входящих в уравнение, имеет вид: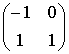 
. Ее определитель не равен нулю, поэтому ранг матрицы равен 2, т. е равняется числу эндогенных переменных без одного. Достаточное условие идентификации выполняется.
Второе уравнение: матрица коэффициентов при переменных, не входящих в уравнение, имеет вид: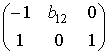 
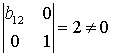
. Ранг данной матрицы равен 2, так как существут определитель второго порядка не равный нулю: 
. Следовательно, достаточное условие идентификации для данного уравнения также выполняется Но в соответствии с необходимым условием считаем это уравнение сверхидентифицируемым.
Таким образом, эта система уравнений является сверхидентифицируемой.
7.5. Методы оценки параметров структурной формы модели
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:
1) косвенный метод наименьших квадратов;
2) двухшаговый метод наименьших квадратов;
3) трехшаговый метод наименьших квадратов;
4) метод максимального правдоподобия с полной информацией;
5) метод максимального правдоподобия при ограниченной информации.
Рассмотрим сущность некоторых из этих методов.
Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов:
1. Для структурной модели строится приведенная форма модели.
2. Для каждого уравнения приведенной формы традиционным МНК оцениваются приведенные коэффициенты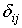 
.
3. На основе коэффициентов приведенной формы находятся путем алгебраических преобразований параметры структурной модели.
Двухшаговый метод наименьших квадратов (ДМНК)
Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод (ДМНК).
Основная идея ДМНК состоит в следующем:
· на основе приведенной формы модели получить для сверхидентифицируемого уравнения расчетные значения эндогенных переменных, содержащихся в правой части этого уравнения;
· подставляя найденные расчетные значения эндогенных переменных вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения.
Метод получил название двухшагового МНК, ибо дважды используется МНК:
· на первом шаге при определении параметров приведенной формы модели и нахождении на их основе оценок расчетных значений эндогенных переменных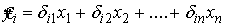 
; 
;
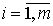
· на втором шаге применительно к структурному сверхидентифицируемому уравнению, когда вместо фактических значений эндогенных переменных рассматриваются их расчетные значения, найденные на предыдущем шаге.
Сверхидентифицируемая структурная модель может быть двух типов:
· все уравнения системы сверхидентифицируемы;
· система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.
Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним можно найти на основе косвенного МНК. Двухшаговый метод, примененный к точно идентифицированным уравнениям дает такой же результат, что и косвенный МНК.
Продолжение примера 15.
Продолжим рассмотрение примера 15.
Система является сверхидентифицируемой: первое уравнение идентифицируемо, а второе уравнение сверхидентифицируемо. Поэтому для определения коэффициентов первого уравнения можно применить косвенный МНК, а для второго уравнении двухшаговый МНК.
Построим приведенную форму модели:
(7.9)
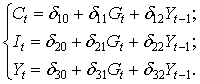
Исходные данные задачи (в млрд. руб.)
| годы | 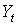 | 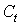 | 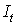 | 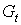 | 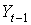 | Предсказанное |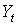
| 4823.23 | 2281.18 | 670.44 | 2629.62 | 4182,05 | ||
| 7305.65 | 3009.42 | 1165.23 | 1014.2 | 4823.23 | 6731,57 | |
| 8943.58 | 3972.81 | 1504.71 | 1193.5 | 7305.65 | 9496,45 | |
| 10830.54 | 5001.77 | 1762.41 | 1947.3 | 8943.58 | 11692,48 | |
| 13243.24 | 6147.26 | 2186.37 | 2345.6 | 10830.54 | 13947,4 | |
| 17048.12 | 7670.68 | 2865.01 | 2659.4 | 13243.24 | 16716,24 | |
| 21625.37 | 9613.84 | 3611.11 | 3472.1 | 17048.12 | 21268,68 | |
| 26903.49 | 11927.59 | 4730.02 | 4284.8 | 21625.37 | 26648,73 | |
| 33258.14 | 14831.38 | 6716.22 | 26903.49 | 33297,77 |
Найдем параметры модели (7.9), применяя МНК к каждому уравнению,
используем « Пакет анализа» EXCEL):
(7.10)
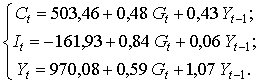
Каждое уравнение статистически значимо (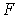 
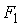
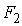
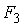
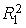
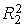
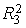
– статистики: 
=1302,55;
=281,956; 
=847,65). Коэффициенты детерминации свидетельствуют о хорошей связи между эндогенными и предопределенными переменными: 
=0,9977; 
=0,989; 
=0,996.
На основе уравнений модели (7.10) найдем структурные коэффициенты первого уравнения.
Выразим из третьего уравнения (7.10) переменную 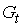и подставим в первое уравнение. Получим первое структурное уравнение: 
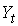
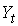
Так как второе уравнение сверхидентифицировано, то применим двухшаговый МНК. Найдем на основе третьего уравнения (7.10) расчетные значения переменной ( столбец «предсказанное » табл.23) и используем их для нахождения параметров второго структурного уравнения.
Получим: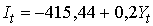 
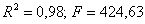
4; 
.
В результате получим следующую систему структурных уравнений:
Трехшаговый метод наименьших квадратов (ТМНК)
Трехшаговый метод наименьших квадратов применяется для оценки параметров системы одновременных уравнений в целом. Сначала к каждому уравнению применяется двухшаговый метод с целью оценить коэффициенты и случайные остатки каждого уравнения. Затем строится ковариационная матрица остатков и проводится ее оценка. После этого для оценивания коэффициентов всей системы применяется обобщенный метод наименьших квадратов. ТМНК является достаточно эффективным, но требует существенно больших вычислительных затрат. Более подробное описание можно найти в работе[1][1]
Видео:Системы одновременных эконометрических уравненийСкачать
Системы эконометрических уравнений
Пример . Рассмотрим модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р):у = а0 + а1х + а2р + ε. Определим класс модели и вид переменных модели: регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания.
Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками спецификации модели.
Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.
- Система независимых уравнений, когда каждая зависимая переменная (y ) рассматривается как функция только от предопределенных переменных (х):
- Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений:
От структурной формы легко перейти к так называемой приведенной форме модели. Число уравнений в приведенной форме равно числу эндогенных переменных модели. В каждом уравнении приведенной формы эндогенная переменная выражается через все предопределенные переменные модели:
Так как правая часть каждого из уравнений приведенной формы содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такая система является системой независимых уравнений. Поэтому параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.
Зная оценки этих приведенных коэффициентов можно определить параметры структурной формы модели. Но не всегда, а только если модель является идентифицируемой.
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать
Проблема идентификации
Количество структурных и приведенных коэффициентов одинаково в модели идентифицируемой.
Видео:ФСР. Система однородных уравнений. Общее решениеСкачать
Правила идентификации
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 1-ое уравнение модели неидентифицированно.
Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствуют переменные y3, x2, х3:
y3 x 2 x3
b13 a 13 0 — в 1-ом уравнении
1 a32 a33 — в 3-ем уравнении
Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 2-ое уравнение модели точно идентифицированно.
Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные y1, x2:
y 1 x 2
1 a12 — в 1-ом уравнении
b21 0 — во 2-ом уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 3-е уравнение модели неидентифицированно.
Сделаем выводы: 1-ое и 3-е уравнения системы неидентифицированны (т.к. не выполняются достаточные условия идентификации, а в случае 1-ого уравнения и необходимое условие также). 2-ое уравнение системы сверхидентифицированно. Следовательно, система в целом является неидентифицируемой.
Для оценки параметров 2-ого уравнения можно применить двухшаговый МНК. Параметры 1-ого и 3-его уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.
Видео:11. Lecture 10. 23nov. Simultaneous equations.Скачать
Условия идентификации структурной формы системы одновременных уравнений
Введём следующие обозначения:
N – количество предопределённых переменных структурной формы системы одновременных уравнений;
n – количество предопределённых переменных в уравнении, проверяемом на идентифицируемость;
M – количество эндогенных переменных структурной формы системы одновременных уравнений;
m – количество эндогенных переменных в уравнении, проверяемом на идентифицируемость;
K – матрица коэффициентов при переменных, не входящих в уравнение, проверяемое на идентифицируемость.
Необходимые и достаточные условия идентификации применяются только к структурной форме системы одновременных уравнений.
Первое необходимое условие идентифицируемости уравнения структурной формы системы одновременных уравнений.
Уравнение структурной формы системы одновременных уравнений идентифицируемо в том случае, если оно исключает хотя бы N-1 предопределённую переменную:
Второе необходимое условие идентифицируемости уравнения структурной формы системы одновременных уравнений.
Уравнение структурной формы системы одновременных уравнений идентифицируемо в том случае, если количество предопределённых переменных, не входящих в данное уравнение, будет не меньше числа эндогенных переменных этого уравнения минус единица:
Достаточное условие идентифицируемости уравнения структурной формы системы одновременных уравнений.
Уравнение структурной формы системы одновременных уравнений идентифицируемо в том случае, если ранг матрицы K равен (N-1).
Рангом матрицы называется размер наибольшей её квадратной подматрицы, определитель которой не равен нулю.
На основе перечисленных условий идентификации, можно сформулировать необходимые и достаточные условия идентифицируемости уравнения структурной формы системы одновременных уравнений:
- уравнение структурной формы системы одновременных уравнений считается сверхидентифицированным, если M–m>n–1 и ранг матрицы K равен (N-1);
- уравнение структурной формы системы одновременных уравнений считается точно идентифицированным, если M–m=n–1 и ранг матрицы K равен (N-1);
- уравнение структурной формы системы одновременных уравнений считается неидентифицированным, если M–m≥n–1 и ранг матрицы K меньше (N-1);
- уравнение структурной формы системы одновременных уравнений считается неидентифицированным, если M–m .
В качестве примера можно рассмотрим процесс идентификации структурной формы модели спроса и предложения. Данная модель включает в себя три уравнения:
1) уравнение предложения:
2) уравнение спроса:
3) тождество равновесия:
С учётом тождества равновесия, модель спроса-предложения может быть записана в виде:
Количество эндогенных переменных данной модели M равно двум (Pt и Qt), т.е. M=2. Количество предопределённых переменных данной модели N равно двум (Pt–1 и It), т.е. N=2.
Проверим выполнение первого необходимого условия идентифицируемости.
Для функции спроса выполняются равенства m=2 и n=1. Отсюда
следовательно, уравнение спроса является точно идентифицированным.
Для функции предложения выполняются равенства m=2 и n=1. Отсюда
следовательно, уравнение предложения является точно идентифицированным.
Проверим выполнение второго необходимого условия идентифицируемости.
Для функции спроса выполняются равенства m=2 и n=1. Отсюда
следовательно, уравнение спроса является точно идентифицированным.
Для функции предложения выполняются равенства m=2 и n=1. Отсюда
следовательно, уравнение предложения является точно идентифицированным.
Проверим выполнение достаточного условия идентифицируемости, заключающееся в том, чтобы хотя бы один из коэффициентов матрицы K не был равен нулю, т.к. M–1=1.
В первом уравнении модели исключена переменная It и матрица K=[b2]. Т.к. определитель данной матрицы не равен нулю, следовательно, rank=1=M–1 и уравнение является идентифицированным.
Во втором уравнении исключена переменная Pt–1 и матрица К=[a2]. Т.к. определитель данной матрицы не равен нулю, следовательно, rank=1=M–1 и уравнение является идентифицированным.
Т.к. уравнения спроса и предложения являются точно идентифицированными, то и система уравнений в целом точно идентифицирована.
Приведённая форма системы уравнений модели спроса-предложения:
🔥 Видео
Системы эконометрических уравненийСкачать
Эконометрия_л9Скачать
Урок 21 (осн). Задачи на одновременное движение телСкачать
7inR 2. Instrumental Variables and Simultaneous Equations ModelsСкачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать
9. Теоремы о сходящихся последовательностях ( свойства сходящихся последовательностей )Скачать
Metrics, 2021-03-05, class IPСкачать
Решение тригонометрических уравнений и их систем. 10 класс.Скачать
Предельные вероятности состоянийСкачать
Числовые Промежутки — Алгебра 8 класс / Подготовка к ЕГЭ по МатематикеСкачать
Старт в анализе данных: как перезапустить карьеру в 2024 годуСкачать
Введение в эконометрику 7 глава 3 часть ИТОГСкачать
Коэффициент детерминации. Основы эконометрикиСкачать
