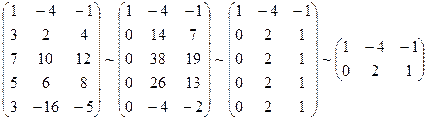Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи». В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde$.
Следствие из теоремы Кронекера-Капелли
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Исследовать СЛАУ $ left <begin& -3x_1+9x_2-7x_3=17;\ & -x_1+2x_2-4x_3=9;\ & 4x_1-2x_2+19x_3=-42. endright.$ на совместность. Если СЛАУ совместна, указать количество решений.
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde$, запишем их:
Видео:Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы «Формулы для вычисления определителей второго и третьего порядков»:
$$ Delta A=left| begin -3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19 end right|=-21. $$
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $rang A=3$.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Способ №2. Вычисление ранга методом элементарных преобразований.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
$$ left( begin 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -3 & 5 & -4 \ 3 & -2 & 5 & 1 \ 2 & -1 & 3 & 2 end right) begin phantom\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1endrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & -1 & 1 & -2 \ 0 & 1 & -1 & 4 \ 0 & 1 & -1 & 4 end right) begin phantom\phantom\r_3-r_2\ r_4-r_2\r_5+r_2endrightarrow\ $$ $$ rightarrowleft( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 end right) begin phantom\phantom\phantom\ r_4-r_3\phantomendrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right) $$
Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $rangwidetilde=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $rang=2$.
Ответ: система несовместна.
Приводим расширенную матрицу системы к ступенчатому виду:
$$ left( begin 2 & 0 & 7 & -5 & 11 & 42\ 1 & -2 & 3 & 0 & 2 & 17 \ -3 & 9 & -11 & 0 & -7 & -64 \ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) overset<r_1leftrightarrow> $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 2 & 0 & 7 & -5 & 11 & 42\ -3 & 9 & -11 & 0 & -7 & -64\ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) begin phantom\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 3 & -2 & 0 & -1 & -13\ 0 & 7 & -1 & -5 & 6 & -5 \ 0 & -3 & 2 & 0 & 1 & 13 end right) begin phantom\ phantom\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end rightarrow $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & -11 & 15 & -25 & -76 \ 0 & 0 & 11 & -15 & 25 & 76 end right) begin phantom\ phantom\phantom \ r_4-r_3 \ r_5+r_2 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 end right) $$
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $rangwidetilde=ranglt$, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Условия несовместности СЛАУ
Определение. Для системы линейных уравнений матрица
А * =
называется расширенной матрицей системы.
Следующая теорема Кронекера-Капелли (Леопольд Кронекер (1823-1891), немецкий математик) устанавливает условие совместности СЛАУ.
Теорема (Кронекера-Капелли).Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы:
Доказательство.Очевидно, что система может быть записана в виде:
x1 


1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А * не изменяют ранга.
2) Если RgA = RgA * , то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Пример 1. Определить совместность системы линейных уравнений:
Решение.Приводим расширенную матрицу системы к ступенчатому виду, чтобы определить ранг матриц.
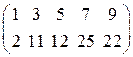
Базисный минор 
A* = 
Система несовместна.
Пример 2. Определить совместность системы линейных уравнений.
Решение. А = 

A* =
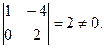
Система совместна.
Пример 3. Решить систему линейных уравнений методом Гаусса.
Решение.Составим расширенную матрицу системы.
А* = 
Таким образом, исходная система может быть представлена в виде:
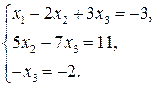
Метод исключения переменных Гаусса для решения СЛАУ.
Условия существования множества решений СЛАУ
(нахождение общего решения СЛАУ)
Лекция 10
Однородные системы линейных алгебраических уравнений, свойства решений.
Понятие фундаментальной системы (ФСР) решений ОСЛАУ. Структура общего решения неоднородной СЛАУ.
Однородные системы линейных алгебраических уравнений,
Свойства решений
Определение 1. Если в каждом уравнении СЛАУ свободные члены равны нулю, то эта система называется однородной.
Однородную систему можно записать в следующем виде:
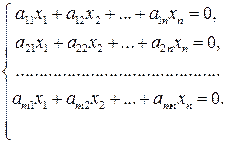
Рассмотрим основные свойства однородных систем.
Теорема 1. Однородная система (15.1) всегда совместна (она имеет, по крайней мере, одно решение – нулевое).
Доказательство теоремы очевидно.
Возникает вопрос: в каком случае система (15.1) будет иметь и ненулевые решения? Ответ на этот вопрос даёт следующая теорема.
Теорема 2.Для того чтобы система (15.1) имела ненулевые решения, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа переменных 
Доказательство.
1. Необходимость.Пусть система имеет ненулевые решения, ранг матрицы системы, по определению, не может быть больше числа переменных, следовательно, 


2. Достаточность.Пусть 
Следствие 1.Если число уравнений в системе (15.1) меньше числа переменных, то система (15.1) имеет ненулевые решения.
Доказательство.Так как 


Следствие 2.Пусть основная матрица системы (15.1) квадратная 
Доказательство.
1. Необходимость.Пусть система (15.1) имеет ненулевые решения, тогда по теореме 

2. Достаточность.Пусть 

Теорема 3.Если 

Доказательство.Так как 

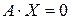

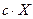
Теорема 4.Если 


Доказательство.Так как 



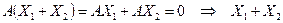
Видео:Теорема Кронекера-КапеллиСкачать

Системы линейных уравнений
Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Классификация систем линейных уравнений
Определение. Две системы называются эквивалентными, если решение первой является решением второй и наоборот.
Определение. Система, имеющая хотя бы одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовместной.
Определение. Система, имеющая единственное решение, называется определенной, а имеющая более одного решения – неопределенной.
📹 Видео
Решение системы уравнений методом ГауссаСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Исследование систем линейных уравнений на совместностьСкачать

Неоднородная система линейных уравненийСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Базисные решения систем линейных уравнений (03)Скачать

Неоднородные системы линейных уравненийСкачать
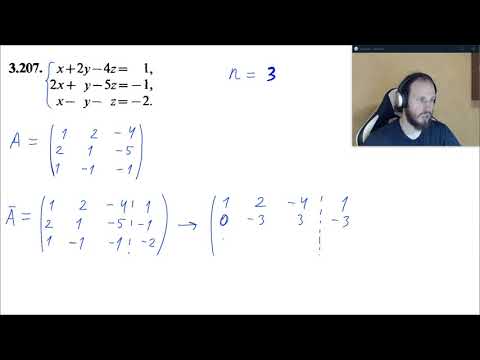
Совместные и несовместные, определенные и неопределенные системы линейных уравненийСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

Тема: Системы линейных уравнений. Урок: Системы линейных уравнений. Геометрическая интерпретацияСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение систем линейных уравнений методом Гаусса. Несовместные системы.Скачать

Совместные и несовместные системы уравненийСкачать