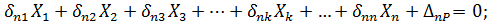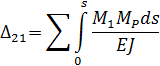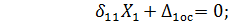Уравнения совместности перемещений порядок их составления

Содержание:

Стержневая система в широком смысле слова — это всякая конструкция, состоящая из элементов, имеющих форму бруса. К таким конструкциям, в частности, относятся фермы, рамы, балки.

Напомним, что статически неопределимыми называют конструкции (стержневые системы) реакции опор и внутренние силовые факторы, в которых, не могут быть определены при помощи уравнений равновесия (статики).

Статически неопределимые системы при растяжении-сжатии.

Цель расчета бруса и стержневой системы (состоящей из отдельных брусьев — стержней), как и любой конструкции — определение размеров поперечных сечении стержней, при которых обеспечивается прочность или жесткость, или и то и другое. Исходя из условий прочности и жесткости при центральном растяжении-сжатии, видим, что в первую очередь необходимо знать экстремальное значение продольной силы.

На рис. 13.1 а стержень опирается на две жесткие опоры. Возникают две реакции и (рис. 13.1 б), величина и направление которых неизвестны, т.к. можно составить только одно уравнение равновесия. В уравнении — два неизвестных осевых усилия:

Задача один раз статически неопределима. Одна связь (опора) — «лишняя».

На рис. 13.1 в — стержневая система, составленная из трех стержней, соединенных шарнирно.

Один раз статически неопределимые системы

Пример решения задачи 1

В стержнях действуют три усилия, направленные вдоль этих стержней. Можно составить только два уравнения равновесия (рис. 13.1 г):

Задача один раз статически неопределима, одна связь (стержень) — «лишняя».

Возможно вам будут полезны данные страницы:

«Лишними» такие связи называют потому, что они не являются необходимыми обеспечения равновесия конструкции и ее геометрической неизменяемости (деформа-стержней и соответствующие ей перемещения отдельных точек систать только от действия внешних сил).

Наличие этих связей обусловлено требованиями к прочности и жесткости конструкции или условиями ее работы.

Для решения задачи по определению неизвестных усилий (говорят — для раскрытия статической неопределимости) необходимо составить дополнительные уравнения. Их количество равно степени статической неопределимости. неизвестных или степень статической неопределимо разностью между числом неизвестных усилий и числом статики. Дополнительные уравнения составляются на основе общего принципа: услов! iccTHocTH деформаций: т.к. стержни соединяются между собой определенным обршарнирно, жестко или в соединении имеются некоторые зазоры, стержни этой cистемы деформируются совместно.

Методику раскрытия статической неопределимости рассмотрим на примере системы (рис. 13.1 в).

Примем, что площадь поперечного сечения боковых стержней одинакова а средний стержень имеет площадь

• 1. Силовая сторона задачи. Составляют уравнения равновесия (в данном случае -два). Они нами составлены ранее. Имеем три неизвестных усилия и два уравнения статики. Система один раз статически неопределима.
• 2. Геометрическая сторона задачи. Рассмотрим перемещения стержней, сходящихся в точке (рис. 13.2). Под действием внешней силы исследуемая точка переместится в положение Концы стержней соединены шарнирно в точке поэтому они получат соответствующие удлинения. Причем эти стержни деформируются совместно, в соответствии с геометрией системы.

Мысленно рассоединим стержни в ненагруженном состоянии (в т. и соединим их в положении после нагружения (в т. Концы крайних стержней переместятся по дуге из т. соответственно в т. и, удлинившись, соединятся в т. Вертикальное перемещение точки весьма мало; угол равен углу дуги можно заменить прямыми, поэтому углы — прямые.

Ввиду симметрии системы, абсолютные удлинения крайних стержней будут равны между собой: Геометрически эти деформации определяются отрезками Средний стержень удлинится на величину отрезка и его удлинение

Рассматривая прямоугольные треугольники можем записать соотношение сторон:

Уравнение (13.2) и есть уравнение совместности деформаций рассматриваемой системы.

3. Физическая сторона задачи. В уравнении совместности деформаций выразим абсолютную деформацию через продольные силы по закону Гука:

Ввиду малости перемещений длина стержней мало меняется и

После преобразований получим зависимость

4. Решение системы уравнений (синтез). Решаем систему уравнений (13.1 и 13.3) и после преобразований получим зависимости, с помощью которых определяются искомые усилия в стержнях:

Видим, что с увеличением площади среднего стержня (с увеличением коэффициента усилие в нем уменьшится; усилия в крайних стержнях также изменятся. В этом отличительная особенность статически неопределимых систем от статически определимых:

повышение жесткости одних элементов приводит к увеличений усилий и, обычно, к снижению усилий в других элементах. В статически определимых системах усилия в элементах не зависят от их жесткости.

Уравнение равновесия составлено нами ранее:

Рассмотрим геометрическую сторону задачи и составим уравнение совместности деформаций для опорных сечений, в которых перемещения равны нулю.

Отбросим мысленно нижнюю опору (рис. 13.3 б). Это опорное сечение станет свободным и переместится вниз за счет абсолютной линейной деформации участка длиной под действием силы С другой стороны, рассматриваемое опорное сечение — неподвижно, следовательно, перемещение его должно равно нулю. Это условие будет выполняться, если реакция на опоре будет по величине и направлению такой, что абсолютная линейная деформация от ее действия окажется равной по величине и противоположной по направлению деформации Условие совместности деформаций запишется в виде:

По закону Гука:

Таким образом, Статическая неопределимость раскрыта.

13.1.1. Расчеты в связи с наличием натягов при сборке конструкций. На практике встречаются и другие задачи, например связанные с неточностью изготовления элементов (стержней).

Неточность изготовления (даже незначительные погрешности) требует приложения дополнительных усилий для сборки узла, при этом возникают натяги и соответствующие монтажные напряжения.

Пример 1 — средний стержень в стержневой системе изготовлен короче проектного размера на малую величину (рис. 13.4 а). Для сборки стержней в узле необходимо средний стержень растянуть, а крайние стержни сжать (рис. 13.4 6).

Неизвестны два усилия. Задача 1 раз статически неопределима. (13.10) Рассмотрим геометрическую сторону задачи (рис. 13.4 в). Крайние стержни будут укорачиваться на величину а средний стержень удлинится на величину Тогда уравнение совместности деформаций запишется в виде:

Ход дальнейшего решения аналогичен порядку решения в предыдущих примерах. Видим, что средний стержень, еще до нагружения внешней силой будет растянут некоторой нагрузкой, т.е. напряжения от натяга будут суммироваться с напряжениями от эксплуатационных нагрузок, что не учитывается в обычных расчетах и может привести к потере прочности.

В качестве примера положительного эффекта от натяга можно привести примеры монтажа бандажа на колесо (металлическое кольцо разогревается и насаживается на колесо, при охлаждении кольцо обжимает колесо), а также предварительно напряженные железобетонные конструкции (в растянутой зоне бетонной плиты располагают предварительно напряженную сжимающими напряжениями стальную арматуру).

Пример решения задачи 2.

Стержень, имеющий жесткость изготовлен короче заданной длины на величину (рис. 13.5 а). Вид расчетной схемы и порядок решения будут зависеть от величины перемещения нижнего сечения (определяемого величиной и положением по длине силы а также жесткостью стержня):

а) величина перемещения нижнего сечения меньше величины зазора — абсолютная линейная деформация стержня Задача статически определима.

б) величина перемещения нижнего сечения больше или равна величине зазора — абсолютная линейная деформация стержня Задача статически неопределима.

Таким образом, в первую очередь, необходимо определить величину перемещения нижнего сечения, которое будет определяться деформацией участка бруса длиной от действия силы

Решение для случая традиционно для решения статически определимых задач.

В случае, если необходимо раскрыть статическую неопределимость.

На опорах возникнут две реакции, величины которых неизвестны (рис. 13.5 б). Уравнение равновесия:

Уравнение совместности деформаций получим, рассматривая схему (рис. 13.5 б):

В соответствии с законом Гука

Получаем: Статическая неопределимость раскрыта.

Расчеты в связи с изменением температуры. Напряжения в сечении стержня также будут возникать даже при отсутствии внешних нагрузок.

Рассмотрим стержень длиной и площадью изготовленный из материала с модулем упругости Оба конца стержня жестко защемлены (рис. 13.6 а). Начальная температура стержня Определить напряжения, которые возникнут в сечении стержня, если он нагревается до температуры Пусть градиент температуры будет положительным:

Как известно, при нагреве материалы расширяются, т.е. стержень будет стремиться удлиниться и распирать опорные сечения, но из-за наличия этих жестких опор, в них возникнут реакции

Уравнение равновесия:

Стержень один раз статически неопределим.

В связи с жестким опиранием, длина стержня изменяться не будет. Т.е. перемещения опорных сечений равны нулю, следовательно, температурная линейная деформация отсутствие одной из опор, например правой (рис. 13.6 б), стержень удлинится на величину Это удлинение должно компенсироваться абсолютной линейной деформацией от действия реакции

Уравнение совместности деформаций:

По известной из курса физики формуле определим температурную деформацию стержня:

где — коэффициент линейного температурного расширения материала стержня, град

По закону Гука Сила сжимает стержень!

Приравняв полученные зависимости, определим значение реакции на опоре и соответствующие температурные напряжения:

Отметим, что температурные (при нагреве стержня) напряжения по знаку — сжимающие. Следовательно, в случае охлаждения такого стержня нормальные напряжения будут растягивающими. Кроме того, видим, что на величину напряжений не влияет длина стержня. Эти обстоятельства следует учитывать в случае использования хрупких материалов, а также, если стержень подвергается действию изменяющихся по величине и знаку температур.

Отметим, что на практике встречаются достаточно сложные схемы стержневых систем, и в каждом конкретном случае задача сводится к геометрическому анализу деформаций и составлению соответствующих уравнений совместности деформаций.

В заключение рассмотрим еще один пример.

Пример решения задачи 2.

Абсолютно жесткий брус (рис. 13.7 а) на стержнях, прикрепленных шарнирами, и нагружен силой Площадь стержней, соответственно, равна Длина стержней Определить значение допускаемой силы из расчета по допускаемым напряжениям и из расчета по разрушающим (предельным) нагрузкам. Материал стержней — сталь

Можно составить два уравнения равновесия для силовой схемы (рис. 13.7 б). Т.к. стержни соединены с жестким брусом посредством шарниров, то усилия в стержнях будут направлены вдоль оси этих стержней:

Первое из них включает и неизвестную реакцию, т.е. имеем три неизвестных. Во втором уравнении неизвестных два — усилия в стержнях. Следовательно, в решении удобнее использовать второе уравнение равновесия.

Рассмотрим геометрическую сторону задачи (рис. 13.7 в). Под действием внешней силы брус, оставаясь прямым (абсолютно жесткий брус — не деформирующийся), повернется вокруг шарнира на некоторый угол. Стержни в местах крепления удлинятся, т.е. точки и переместятся вертикально в положения Отрезки — абсолютные линейные деформации стержней. Из подобия треугольников имеем:

Получили уравнение совместности деформаций.

Подставляем в полученное уравнение усилия в соответствии с формулой закона Гука (физическая сторона задачи).

Решаем систему уравнений Получаем значения усилий в стержнях в долях силы

Расчет по допускаемым напряжениям.

Из условия прочности с учетом, что максимальные нормальные напряжения возникают во втором стержне, имеем:

Решаем уравнении относительно силы

Расчет по разрушающей нагрузке (см. 5.2.2).

Материал стержней — сталь, т.е. пластичный материал. Следовательно, после достижения напряжения во втором стержне (как в более нагруженном) значения предела текучести, этот стержень нагружаться не будет (напряжения не растут, увеличиваются деформации — см. диаграмму растяжения на площадке текучести). Нагрузку будет воспринимать первый стержень. Таким образом, и уравнение (5.30) примет вид:

Откуда получаем значение силы, при котором в обоих стержнях напряжения достигнут предела текучести — предельная грузоподъемность системы:

Разделим предельное значение силы на коэффициент запаса и получим допускаемое значение силы:

Видим, что при расчете во втором случае допускаемая нагрузка выше, чем в первом на величину т.е. расчет по разрушающим нагрузкам дает возможность в большей степени использовать свойства материала и особенности стержневой системы.

Основы расчета статически неопределимых систем, работающих на изгиб. Анализ структуры простейших стержневых систем

Указанный анализ проведем на примере рам. В зависимости от взаимного расположения осей стержней и силовых плоскостей, рамы подразделяются на:

плоские стержневые системы (рамы, балки) — оси стержней и все внешние силы лежат в одной плоскости (рис. 13.8 а, б)

плоско-пространственная системы — оси составляющих элементов в недеформиро-ванном состоянии лежат в одной плоскости, а внешние нагрузки лежат в другой — перпендикулярной плоскости (рис. 13.8 в);

пространственная система — силы и оси стержней могут находиться в произвольно расположенных плоскостях (рис. 13.8 г).

Понятие о степенях свободы и связях. Известно, что в пространстве тело обладает шестью степенями свободы, а в плоскости — тремя. Независимая координата определяющая положение тела в плоскости или пространстве , называется степенью свободы.

Ограничения которые накладываются на тело называются связями. Каждая связь снимает одну степень свободы.

Количество связей накладывемых на тело ( стержневую систему) может быть любым . Для обеспечения равновесия и неподвижности тела в плоскости или пространстве необходимо и достаточно снять соответствующие количество степеней свободы — иначе говоря наложить соответсвующие число связей Эти связи — необходимые .

Всякая связь наложенная сверх необходимой — дополнительная ( лишняя) связь . В сопротивлении материалов и строительной механике связи разделяются на внешние ( опорные) и внутренние

Опорные связи — связи, накладываемые опорными устройствами, (рис. 13.9 а):

• шарнирно-подвижная опора накладывает одну связь (снимает одну степень свободы);

• шарнирно-неподвижная — соответственно две;

• в заделке на опорное сечение стержня накладывается три связи.

Внутренние связи ограничивают взаимное перемещение стержней в сечениях, где они соединяются (рис. 13.9 б):

• жесткое соединение двух стержней накладывает три связи; • шарнирное соединение двух стержней — две связи;

• три стержня, соединенные жестко, — шесть связей;

• три стержня, соединенные шарнирно, — четыре связи. Таким образом, шарнир снимает одну связь.

Анализ рис. 13.9 б позволяет сделать вывод о том, что шарнир, включенный в узел, где сходятся стержней, снижает степень статической неопределимости на

Определение степени статической неопределимости. Реакции, возникающие в «лишних» связях — «лишние» неизвестные. Уравнений равновесия оказывается недостаточно для решения задачи — определения опорных реакций. Как известно, такие задачи называют статически неопределимыми. Степень статической неопределимости определяется числом лишних связей.

В строительной механике используются различные формулы для определения степени статической неопределимости или числа лишних связей Л. Приведем одну из них:

где — число стержней (в строительной механике — дисков).

Рассмотрим примеры стержневых систем — плоских рам (рис. 13.10) и определим степень их статической неопределимости расчетом по формуле (13.18).

число лишних связей т.е. система статически определима;

т.е. система 2 раза статически неопределима (внешним образом, т.к. лишними являются 2 опорные связи);

т.е. система 3 раза статически неопределима (внутренним образом, т.к. лишними являются 3 внутренние связи).

Заметим, что жесткий замкнутый контур трижды статически неопределим (внутренним образом);

т.е. система 6 раз статически неопределима (3 раза внешним образом и 3 раза — внутренним образом). Заметим, что в данной схеме фактически имеем два жестких замкнутых контура;

Геометрическая и кинематическая неизменяемость. Геометрический и кинематический анализ стержневых систем подробно излагается в дисциплине «Строительная механика».

Под действием нагрузок сооружение (стержневая система) деформируется, и его точки перемещаются (при этом изменяется также и форма сооружения).

Если указанные перемещения возможны только за счет деформации стержней (элементов сооружения), то стержневая система называется геометрически неизменяемой (рис. 13.11 а). Иначе говоря, в элементах конструкции должны отсутствовать перемещения точек, не связанные с деформацией этих элементов под действием нагрузки. В сопротивлении материалов и строительной механике рассматриваются только такие конструкции (в том числе и стержневые системы).

а — система соединенных между собой ные перемещения стержней деформации. Геометрически изменяемые системы (рис. 13.11 б) — это по сути механизмы. Перемещения точек элементов такой системы возможны без деформирования стержней (элементов конструкции).

изменяемая система — система соединенных между собой стержней, допускающая конечные перемещения стержней

без их деформации.

Кинематически изменяемая система (ее еще называют мгное мая система)- система соединенных между собой стержней, допускающая мации тела бесконечно малые относительные перемещения, после чего система

становится неизменяемой. Геометрическими признаками мгновенно изменяемых систем являются следующие:

• шарниры или шарнир и стержень находятся на одной прямой;

• стержни параллельны или пересекаются в одной точке.

Метод сил. Основная система.

Для раскрытия статической неопределимости стержневых систем в машиностроении применяют метод сил.

Неизвестными оказываются силы. Отсюда и название «метод сил» (в строительной механике применяется также и метод перемещений).

Метод сил заключается в том, что заданная статически неопределимая система освобождается от лишних связей, а их действие заменяется усилиями по направлению этих связей.

Величина усилий подбирается таким образом, чтобы перемещения по их направлениям соответствовали тем ограничениям, которые накладываются на систему

Рассмотрим метод сил на примере статически неопределимой рамы. Решение задачи (раскрытие статической неопределимости) начинаем с отбрасывания лишних связей. Система освобождается от лишних связей и становится статически определимой.

Статически определимая и геометрически неизменяемая система, полученная из заданной путем отбрасывания «лишних» связей — основная система.

Таких систем можно составить сколь угодно много. Примеры основных систем, составленные для заданной статически неопределимой системы (рис. 13.12 а) приведены на рис. 13.12 б-з. Схема (рис. 13.12 и) — не является основной, т.к. три шарнира располагаются на одной прямой. Это кинематически изменяемая система.

Продолжая решение задачи, в основной системе приложим внешние нагрузки и усилия (силовые факторы) по направлению отброшенных связей, которые мы назвали «лишними» неизвестными. Усилиями по направлению отброшенных связей являются силы и моменты. Силы ограничивают линейные перемещения, а моменты — соответствующие угловые перемещения.

Направление усилий выбирают произвольно:

• вправо или влево;

• по часовой или против часовой стрелки.

Неизвестные усилия обозначаем — номер силового фактора. Число этих неизвестных будет соответствовать степени статической неопределимости, причем направления этих связей являются взаимными.

Основная система, в которой приложены внешние нагрузки и усилия по направлению отброшенных связей называется эквивалентной системой.

Каждой основной системе будет соответствовать своя эквивалентная система (рис.13.13).

Рассмотрим, например, заданную схему (рис. 13.12 а), выберем для нее основную (рис. 13.12 б) и изобразим эквивалентную системы (рис. 13.14). В заданной схеме линейные перемещения (горизонтальное и вертикальное) на опоре и линейные и угловое перемещения в сечении на верхнем ригеле запрещены. Но они же разрешены в основной системе. Неизвестные усилия, показанные в эквивалентной системе, по величине и направлению должны обеспечить равенство нулю указанных перемещений.

Взаимное смещение точек системы условимся обозначать следующим образом

где:

первый индекс — направление по которому определяется перемещение, второй индекс — причина, вызвавшая это перемещение,

— направление перемещения (по направлению неизвестных сил

— сила, вызвавшая перемещение (неизвестные силы

— любая система внешних нагрузок.

В точках (рис. 13.14) перемещения будут определяться действием всех сил, приложенных к системе — как внешних нагрузок так и неизвестных усилий При этом, в соответствии с особенностями расчетной схемы, эти перемещения должны быть равны нулю. Запишем, систему уравнений

Используя принцип независимости действия сил, для любого количества неизвестных можно записать:

В этих формулах индексы — номера неизвестных сил.

— единичное перемещение по направлению силы от действия единичной силы

— единичное перемещение по направлению силы от действия единичной силы

— единичное перемещение по направлению силы от действия единичной силы

— соответственно, перемещения в направлении единичных сил от действия системы внешних сил

Известно, что перемещения пропорциональны действующим силам. Тогда

Обобщая, имеем

Учитывая (13.21) перепишем (13.20) и получаем:

каноническое уравнение метода сил

— главные коэффициенты уравнений,

— побочные коэффициенты уравнений (по теореме Максвелла их значения попарно равны),

— свободные члены уравнений.

Количество записываемых канонических уравнений метода сил соответствует количеству «лишних» неизвестных (степени статической неопределимости). Остается определить коэффициенты уравнений и, решив систему уравнений, найти значения и направления

Для понимания геометрического смысла коэффициентов уравнений рассмотрим два раза статически неопределимую раму (рис. 13.15), где графически покажем рассмотренные выше перемещения.

Коэффициенты определяются методом Мора, чаще перемножением эпюр по способу Верещагина.

При определении коэффициентов канонических уравнений методом перемножения эпюр (по Верещагину):

1. Строим единичные эпюры изгибающих моментов. Единичные эпюры строятся для основной системы от каждого «лишнего» неизвестного, т.е. в основной системе поочередно прикладываются неизвестные, равные единице, определяются реакции и строится единичная эпюра.

Единичных эпюр, должно быть столько, какова степень статической неопределимости рамы.

Получим единичные эпюры изгибающих моментов

2. Строим грузовую эпюру изгибающих моментов. Эта эпюра также строится для основной системы: в этой системе прикладываются все внешние нагрузки (силы, моменты, распределенные нагрузки), которые имеются на заданной схеме, определяются опорные реакции и стоится грузовая эпюра

3. Перемножаем эпюры по способу Верещагина и находим значения коэффициентов канонических уравнений:

главные коэффициенты получаем, перемножая единичные эпюры «сами на себя», т.е. в качестве грузовой рассматривается та же единичная эпюра: Или по формуле Верещагина

побочные коэффициенты определяются перемножением единичных эпюр в соответствии с записью т.е. одна из единичных условно считается грузовой. По Верещагину

свободные члены определяются перемножением грузовой эпюры, поочередно, на единичные в соответствии с записью По Верещагину

4. Подставляем значения вычисленных коэффициентов в систему канонических уравнений, решаем ее и определяем значения

Если значения некоторых неизвестных получаем со знаком минус, это значит, что действительное направление их обратно по отношению к принятому в эквивалентной системе. Желательно при продолжении решения (при построении окончательных эпюр) поменять направление этих неизвестных.

5. В эквивалентной системе вместо неизвестных усилий прикладываем их значения (в положительном направлении), определяем опорные реакции и строим эпюры

6. Проводится проверка правильности расчетов (см. 11.3.2).

Расчет статически неопределимых рамных систем

Рациональный выбор основной системы.

Основная система (удовлетворяющая выше приведенным требованиям) может быть любой, но трудоемкость расчетов будет различной:

а) учитывая, что в процессе решения нужно строить и перемножать эпюры, лучше выбирать такой вариант основной системы, для которого легче эти эпюры строить;

б) протяженность эпюр и их очертания должны быть, по возможности, простыми;

в) для некоторых схем рам возможно использование свойств симметрии и кососим-метрии (рис.13.16).

Положительный эффект учета свойств симметрии и кососимметрии поясним на примере (рис. 13.17). В заданной схеме рамы приложена кососимметричная нагрузка. Основная система и неизвестные усилия являются симметричными.

Прикладываем в основной системе поочередно неизвестные усилия и внешнюю нагрузку и строим эпюры изгибающих моментов. Получаем симметричные и кососимметричные эпюры.

Следовательно, соответствующие коэффициенты канонических уравнений будут равны нулю, и решение этих уравнений упрощается. Например:

Таким образом, в нашем примере будут равны нулю коэффициенты:

и система канонических уравнений

Следовательно Получим одно уравнение:

Таким образом, вместо решения системы трех уравнений, достаточно решить одно уравнение. Соответственно, вместо трижды статически неопределимой системы имеем один раз статически неопределимую систему.

В том случае, если в рассмотренном примере внешние нагрузки будут приложены симметрично (так, как показано на рис. 13.16 ), то и эпюра будет симметричной. Тогда

Получаем систему уравнений

Видим, что в этом случае только равно нулю, т.е. необходимо решать систему двух уравнений.

Проверка правильности расчетов.

Проверка должна проводиться на всех этапах решения:

• правильность выбора основной системы; соответствие эквивалентной системы выбранной основной; правильность определения реакций во всех расчетных схемах; правильность построения эпюр: единичных и грузовой эпюр изгибающих моментов;

правильность определения коэффициентов канонических уравнений; правильность решения системы уравнений;

• правильность построения окончательных эпюр

Однако, подтверждением правильности решения задачи, является так называемая деформационная проверка. Деформационная проверка заключается в том, что исполнитель расчета должен убедиться, что перемещения по направлению любой из отброшенных связей.

Для этого окончательную эпюру изгибающих моментов перемножают поочередно на каждую из единичных эпюр. И желательно на те единичные, которые не использовались в расчете, т.е. для другой основной системы. Более надежной является проверка, которая проводится путем сравнения некоторых сумм коэффициентов уравнений (полученных в расчете) и результатов перемножения эпюр.

Дополнительно строят суммарную единичную эпюру Ее легко построить графически, суммировав единичные эпюры

А) построчная проверка заключается в сравнении сумм коэффициентов по строкам с результатом перемножения суммарной единичной эпюры с каждой из единичных:

Б) универсальная проверка заключается в сравнении суммы всех главных побочных коэффициентов с результатом перемножения суммарной единичной эпюры самой на себя:

Рассмотрим пример расчета статически неопределимой плоской рамы методом сил.

Для рамы (рис. 13.18 а) построить эпюры Определить вертикальное перемещение точки

1. Определяем степень статической неопределимости

2. Выбираем основную систему и строим для нее эквивалентную систему

3. Записываем систему из двух канонических уравнений метода сил:

4. Строим единичные и грузовую эпюры изгибающих моментов. Для уменьшения объема рисунка совместили единичные и грузовую схемы с соответствующими эпюрами.

5 Метод Верещагина определяем коэффициенты канонических уравнений

Коэффициенты вида имеют размерность В данной задаче все коэффициенты безразмерны, т.к. нагрузки и размеры заданы в общем виде. При перемножении эпюр учитываем общие границы участков.

6. Подставляем найденные значения коэффициентов в систему канонических уравнений. Определяем значения

7. Прикладываем найденные значения неизвестных усилий в эквивалентной системе (рис. 13.18 б). Вслучае если найденное значение неизвестного усилия получаем со знаком (-), его направление меняем на противоположное.

8. Строим эпюры

9. Контроль правильности построения эпюр и всего расчета (деформационная проверка).

9.1. Перемножаем по методу Верещагина эпюру поочередно на единичные эпюры и определяем вертикальное и горизонтальное перемещения шарнирно неподвижной опоры.

Перемножим эпюры

Погрешность расчета (в сравнении с нулем):

Перемножим эпюры

Погрешность расчета (в сравнении с нулем):

Решение выполнено правильно. Рассмотрим другой возможный вариант основной системы (рис. 13.19).

Видим, что очертания эпюр совпадают с такими же единичными эпюрами на рис. 13.18 (отличаются только значения ординат на эпюре Следовательно, и результаты перемножения совпадут.

Правильность решения задачи подтверждается.

Проведем проверки, рекомендованные ранее. Для этого построим суммарную единичную эпюру (рис. 13.20), сложив единичные эпюры (см. рис. 13.18).

Универсальная проверка:

Результаты проверки подтверждают правильность решения задачи.

На странице -> решение задач по сопротивлению материалов (сопромат) собраны решения задач и заданий с решёнными примерами по всем темам сопротивления материалов.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Расчет статически неопределимой стержневой системы. Уравнение совместимости деформацийСкачать

Упругость анизотропных материалов (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

Упругость анизотропных материалов

Видео:Перемещения при изгибе. Часть 1. Дифференциальное уравнение изогнутой оси бруса.Скачать

Оглавление

1 Теория деформаций
1.1 Введение
1.2 Малые деформации
1.3 Малые вращения
1.4 Уравнения совместности деформаций
1.5 Вычисление перемещений по полю деформаций
2 Теория напряжений
2.1 Введение
2.2 Принцип напряжений
2.3 Тензор напряжений
2.4 Вычисление вектора напряжений
2.5 Уравнения равновесия в напряжениях
2.6 Условия равновесия на поверхности
2.7 Главные напряжения и направления
3 Определяющие соотношения УАМ
3.1 Общая характеристика определяющих соотношений
3.2 Обобщенный закон Гука
3.3 Упругий потенциал
3.4 Частные случаи анизотропии упругих свойств
3.5 Технические постоянные УАМ
4 Краевые задачи УАМ
4.1 Общая характеристика полной системы уравнений УАМ
4.2 3 типа граничных условий УАМ
4.3 Полная система уравнений в перемещениях
4.4 Граничные условия краевой задачи в перемещениях
4.5 Работа внешних сил
4.6 Теорема об единственности решения

Видео:Определение усилий, напряжений и перемещений. СопроматСкачать

Введение

Упругость анизотропных материалов — раздел механики, объектом изучения которого является модель материала или конструкции. Модель наделяется теми или иными свойствами, характерными для данного материала. Задачей упругости анизотропных материалов является изучение равновесия внутреннего состояния материалов и тел.

Внутреннее состояние характеризуется с помощью ряда величин: напряжения, деформации, температуры и т. д. Построение модели материала основывается на понятии материального континуума1. При изучении внутреннего состояния в упругости анизотропных материалов рассматривается макроскопическое поведение материалов2.

Задачи упругости анизотропных материалов во многом близки к задачам сопротивления материалов, однако, в сопротивлении материалов напряжения и деформации, характеризующие внутреннее состояние изучаются на основе совокупностей геометрических и физических гипотез, при этом напряжения и деформации рассчитываются с помощью простых математических формул, которые сами по себе являются достаточно приближенными. В упругости анизотропных материалов внутреннее состояние изучается с помощью математических моделей, соответствующих законам механики.

Преимущества упругости анизотропных материалов как дисциплины перед сопротивлением материалов заключаются в:

· более точном описании внутреннего состояния (то есть в более точном расчете напряжений и деформаций);

· возможности определения степени достоверности формул сопротивления материалов для конкретных конструкций и условий их нагружения;

В упругости анизотропных материалов принимаются основные гипотезы и предположения. Эти гипотезы используются при построении математических моделей материалов и конструкций:

1. Гипотеза сплошности.

2. Гипотеза твердости.

3. Гипотеза упругости.

— свойство материала оставаться без различного рода разрывов как до воздействия на него, так и после.

— способность материала или конструкции сохранять форму при физическом воздействии на него.

— способность материала или конструкции полностью восстанавливать свою форму и размеры после снятия нагрузки.

— способность восстанавливать форму и размеры мгновенно.

Таким образом, в упругости анизотропных материалов модель материала или конструкции наделяется свойствами твердости, сплошности и идеальной упругости.

В упругости анизотропных материалов вводится понятие о естественном начальном состоянии. Предполагается, что до физического воздействия3 внутреннее состояние материала или конструкции таково, что деформации и напряжения отсутствуют во всех точках. После снятия нагрузки материал или тело возвращается в исходное состояние.

Видео:Химия | Молекулярные и ионные уравненияСкачать

Глава 1
Теория деформаций

1.1 Введение

Описание деформации тела связано с изучением кинематики материала. Материал при деформации рассматривается как совокупность точек, взаимное расположение которых изменяется в результате физических воздействий на материал или тело. Гипотеза сплошности приводит к тому, что соседние материальные частицы, которые были смежными в естественном начальном состоянии остаются смежными и в деформированном состоянии. Это физическая интерпретация того, что изменение материала происходит непрерывно, при этом никакая материальная частица не превращается в объем исчезающе малый или бесконечно большой.

При деформировании сплошной среды все материальные частицы могут получать перемещения. В основе классической теории деформаций лежит метод описания кинематики сплошной среды с помощью вычисления удлинений линейных элементов и изменений углов между линейными элементами, имеющими общую вершину.

— отрезок, соединяющий 2 бесконечно близкие точки.

Способ описания кинематики сплошной среды, связанный с линейными элементами является предпочтительным по отношению к описанию полных перемещений всех точек материала, поскольку позволяет исключить перемещение точки, не связанные с изменением внутреннего состояния.

Если линейные элементы в естественном начальном состоянии в искомой точке были направлены вдоль осей координат Xk , то удлинения этих элементов вычисляются следующим образом:

где Λν(k) — удлинение линейного элемента, направленного вдоль оси Xk, Eν(k) — относительное удлинение линейного элемента, направленного вдоль оси Xk, Ekk — диагональные компоненты тензора деформаций Eij, которые можно вычислить, если известна векторная функция перемещений всех точек среды.

= (X 1,X2,X3) — непрерывная и дифференцируемая функция координат. При этом Eij связан с проекциями вектора перемещений U следующим соотношением:

Изменения углов вычисляется следующим образом: пусть один линейный элемент в некоторой точке в естественном состоянии направлен вдоль оси Xi, а другой — вдоль оси Xj.

1 — Θij — угол между элементами в не деформируемом состоянии; 2 — ϑij — угол в деформированном состоянии; γij = Θij — ϑij — изменение угла между линейными элементами с одной общей вершиной.

Из гипотезы о твердости материала следует, что перемещение точек при деформировании являются малыми, также малыми величинами являются относительные удлинения линейных элементов и изменение углов между линейными элементами1.

В силу малости производных от перемещений, вследствие твердости материалов и тел, произведением производных в выражении (1.2) можно пренебречь по отношению к самим производным. И тогда для твердых тел и материалов выражение (1.2) преобразуется к виду:

При этом тензор Eij является малой величиной порядка α.

В формуле (1.5) величины Ekk являются диагональными элементами тензора деформации Eij и имеют однозначный физический смысл: являются относительными удлинениями линейных элементов, направленных до деформации вдоль осей координат Xk.

С учетом малых величин2 выражение (1.3) преобразуется к виду:

Из формулы (1.6) видно, что недиагональные элементы тензора Eij , в случае малости деформаций, также имеют физический смысл: они равны половине величины изменения прямого угла, который в недеформированном состоянии был образован линейными элементами, направленными вдоль осей Xi и Xj.

1.2 Малые деформации

Если перемещения и их производные считать малыми величинами, то при описании перемещений точек среды функциями компонент Ui(X1,X2,X3) вектора перемещений = (U 1,U2,U3) можно вывести тензор, который называется тензором малых деформаций и обозначается как εij = Eij (тензор деформаций Коши):

Из выражения (1.7) следует, что тензор εij является симметричным3. Само выражение (1.7), которое связывает перемещения точек с тензором деформаций называется геометрическим соотношением Коши или геометрическим соотношением теории малых деформаций. Диагональные элементы тензора εij вычисляются следующим образом:

Для не диагональных элементов:

Поскольку εij является тензором второго ранга, то при повороте системы координат вокруг своего центра компоненты тензора деформаций в новой системе координат вычисляются по следующей формуле:

Где εmn — компоненты тензора в исходной системе координат, а αpq — матрица поворота системы координат:

Для любого произвольно заданного тензора деформаций εij можно найти также положение осей координат (то есть такую новую систему координат по отношению к исходной), что тензор деформаций в новой системе координат будет иметь только диагональные компоненты.

Эти компоненты называются главными линейными деформациями4.

Для тензора малых деформаций, также как и для любого симметричного тензора второго ранга, существуют инварианты, то есть величины, вычисляемые через компоненты тензора и не изменяющие свои значения при повороте системы координат. Для произвольного поворота системы координат вокруг центра, инварианты тензора деформаций имеют вид:

Iε(1) — изменение объема материальной частицы в деформированном состоянии.

При повороте системы координат вокруг одной из осей количество инвариантов увеличивается. Например, вокруг оси X3:

Кинематически допустимым полем перемещений для материала называются однозначные непрерывные и дифференцируемые функции компонент вектора перемещений точек среды. Если же рассматривается область, ограниченная поверхностью, и на всей этой поверхности или на ее части заданы перемещения точек, то на кинематически допустимое поле перемещений накладывается дополнительное условие, а именно: функции компонент тензора перемещений на границе области должны принимать заданные значения.

1.3 Малые вращения

Тензор εij связан с перемещениями:

В соотношении (1.12) используется сокращенная тензорная форма записи производных. Само соотношение (1.12) полностью эквивалентно соотношению (1.7), в котором использована полная тензорная форма записи производных. Если независимыми переменными являются переменные Xj = (X1,X2,X3) и существует произвольная скалярная функция f(X1,X2,X3), то частные производные в цифровой индексной форме записываются: , , , в тензорном виде: , а в сокращенном виде: fi, j.

Рассмотрим наряду с симметричным тензором εij антисимметричный тензор, построенный по соотношению, аналогичному (1.12):

Тензор деформаций εij имеет 9 компонент, из них 6 независимых (в силу симметрии). Антисимметричный тензор ωij тоже имеет 9 компонент, из которых независимыми являются только 3: ω12 , ω13 , ω23. Тензор ωij называют тензором малых вращений. Можно показать, что если при заданном поле перемещений в какой либо точке тензор деформаций εij = 05, то тензор ωij задает малое вращение среды вокруг данной точки, причем окрестность среды вращается как абсолютно твердая. Это малое вращение происходит за счет деформаций других точек этой окрестности.

1.4 Уравнения совместности деформаций

Тензор деформаций в точке вызывает изменение геометрии элементарной частицы, выделенной вокруг этой точки. Из гипотезы сплошности следует, что смежные элементарные частицы не могут деформироваться как угодно произвольно, они должны деформироваться совместно с тем, чтобы среда и в деформированном состоянии оставалась сплошной (непрерывной). Математически это означает, что компоненты тензора деформаций εij как функции координат εij = εij(X1,X2,X3) не могут быть произвольно заданы, а должны удовлетворять некоторому условию или каким-то уравнениям, обеспечивающим сплошность среды в деформированном состоянии. Такие уравнения называют уравнениями совместности деформаций.

Наряду с этими тензорами можно ввести тензор относительных перемещений:

Видео:Механическая система со связями. Идеальные связи и уравнения Лагранжа 1-го рода.Скачать

Определение перемещений упругих систем

Лекция 5. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ

Общие сведения.

Статически неопределимой называется такая система, у ко­торой внутренние силы и реакции не могут быть найдены только из одних уравнений равновесия. Кинематическим признаком ста­тически неопределимых систем является наличие в их структуре так называемых лишних связей, дающих лишние неизвестные сверх определяемых из уравнений статики. Число лишних связей и определяет степень статической неопределимости системы. Для силового расчета статически неопределимой системы кроме уравнений статики надо по числу лишних неизвестных составить дополнительные уравнения на основании рассмотрения дефор­маций системы.

Различают внешне статически неопределимые и внутренне статически неопределимые системы. Система, которая имеет только лишние опорные закрепления, называется внешне статически неопределимой. Система, имеющая лишние связи в своем внутреннем образовании, называется внутренне статически не­определимой. Следует заметить, что деление это условно и, как будет показано ниже, зависит от того, какие связи принимаются за лишние. Могут быть также системы одновременно внешне и внутренне статически неопределимые. Необходимо обратить вни­мание на следующие особенности статически неопределимых систем:

1) Перемещения и усилия в этих системах, как правило, меньше перемещений и усилий в статически определимых системах, из которых они образованы, что ведет к экономии металла; это осо­бенно важно для подвижных подъемно-транспортных машин.

2) Эти системы оказывают большее сопротивление разруше­нию, чем статически определимые, так как удаление лишних свя­зей обычно не ведет к разрушению системы.

3) Внутренние усилия в системах с лишними связями зависят не только от внешних сил, но и от соотношения поперечных сече­ний отдельных элементов, формы сооружения, а также от количе­ства и жесткости лишних связей, поэтому расчет многократно статически неопределимых систем осуществляется методом после­довательных приближений. При этом сначала задаются попереч­ными сечениями всех элементов или определяют их каким-либо упрощенным методом, а затем в ходе окончательного расчета их уточняют.

4) В качестве недостатка статически неопределимых систем следует отметить их чувствительность к изменению температуры, к неточности изготовления отдельных элементов, к смещению и осадкам опор. В результате этих воздействий в них возникают дополнительные напряжения.

5.2 Установление степени статической неопределимости
и выбор лишних неизвестных

Рассмотрим на простых примерах, как устанавливаются лиш­ние связи, при отбрасывании которых система превращается в ста­тически определимую и геометрически неизменяемую. Например, портал с жесткими узлами, представленный на рис. 5.1, а, яв­ляется один раз внешне статически неопределимой системой. За лишнюю неизвестную нужно выбрать горизонтальную реакцию одной из опор и превратить ее из неподвижной в подвижную.

Рисунок 5.1 Примеры один раз статически неопределимых систем

На рис. 5.1, б показана трехопорная балка, также один раз стати­чески неопределимая. Лишней неизвестной является вертикаль­ная реакция одной из подвижных опор. Если эту опору убрать, балка делается статически определимой. Если же в этой балке ввести шарнир, например в сечении к, то она будет статически определимой (рис. 5.1, в), так как появляется дополнительное уравнение статики (сумма моментов всех сил относительно шар­нира равна нулю).

Пример дважды статически неопределимого портала приведен на рис. 5.2.

Рисунок 5.2 . – Пример дважды статически неопределимой системы

В данном случае в качестве одного лишнего неизвестного можно принять горизонтальную реакцию у одной из опор, а другого — усилие в шарнирно прикрепленной к стойкам затяжке АВ. В этом случае портал будет один раз внешне и один раз внутренне статически неопределим.

Для установления степени статической неопределимости в рамных системах необходимо ввести понятия жесткого замкнутого контура и числа простых цилиндрических шарниров. Жестким замкнутым контуром называется контур, состоящий из ряда элементов, жестко связанных между собой и образующих замкнутую цепь. Если рамная система содержит К замкнутых бесшарнирных контуров, то она будет 3К раз статически неопределимой, так как в каждом замкнутом контуре имеются шесть неизвестных и три уравнения статики (рис. 5.3).

Рисунок 5.3 .– Неизвестные параметры в замкнутом контуре

При наличии в замкнутом контуре шарнира статическая не­определимость снижается на единицу, так как появляется допол­нительное уравнение статики. Тогда Л = 3К — Ш, где Л — число лишних связей системы; Ш — число шарниров. На основании этого легко установить степень статической неопределимости любых рамных систем, в которые входят замкнутые контуры и шарниры. Например, в конструкции портала, представленной на рис. 5.4, а, имеется два замкнутых контура; следовательно, он шесть раз статически неопределим.

Рисунок 5.4 . – Схемы портальных рам

В конструкции портала, по­казанной на рис. 5.4, б, в верхнем контуре имеется шарнир. Если рассечь ригель по этому шарниру, то в нем будут две неизвестные внутренние силы N и Q. Поэтому верхний контур будет дваждыстатически неопределимым. Нижний замкнутый контур не имеет шарниров, и, следовательно, он будет трижды статически неопре­делимым, и общая статическая неопределимость будет равна пяти ( Л = 2 x 3 — 1 = 5).

5.3 Канонические уравнения метода сил

Различают три метода расчета статически неопре­делимых систем: метод сил, метод перемещений и метод конечных элементов.

Расчет по методу сил статически неопределимых систем в кра- ностроении является наиболее распространенным. В этом методе расчета в качестве неизвестных принимаются внутренние усилия в лиш­них связях.

Расчет начинают с выбора основной системы. Основной называют такую статически определимую и геометрически неиз­меняемую систему, которая после удаления лишних связей в за­данной системе и замены их неизвестными усилиями находится в таком же напряженно-деформированном состоянии, что и за­данная система. Следует иметь в виду, что для одной и той же заданной системы может быть несколько вариантов основной си­стемы. Поэтому нужно стремиться к наиболее рациональной основ­ной системе, в наибольшей степени упрощающей расчет.

После выбора основной системы расчет осуществляется в сле­дующей последовательности. К основной системе кроме заданной нагрузки по направлению отброшенных связей прикладываются неизвестные силы, называемые лишними неизвестными: Х₁, Х₂, Х₃ и т. д. Неизвестные силы подбираются с таким расчетом, чтобы перемещения в основной и заданной системах были равны. Перемещения по направлению какой-либо неизвестной силы будут равняться нулю независимо от того, где она приложена — на опоре или в рассеченном элементе, поскольку в заданной системе перемещения по направлению неизвестных сил отсутствуют

Следующим этапом расчета будет составление уравнений сов­местности перемещений, которые выражают условие равенства нулю перемещений по направлению каждой лишней связи.

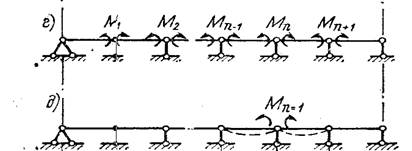
Рассмотрим, например, приведенную на рис 5.5, а неразрез­ную балку с числом лишних связей, равным п. Основную систему выберем путем удаления лишних опорных стержней и замены их неизвестными силами (рис. 5.5, б). Необходимо отметить, что этот вариант основной системы не является оптимальным для решения данной задачи. Более рациональным является выбор основной системы, представленной на рис. 5.6, так как в этом случае значительная часть коэффициентов уравнения обращается в ноль. Столь неудачный в данном случае выбор основной системы сделан в методических целях для того, чтобы сохранить в системе канонических уравнений все их члены. В этом случае система п уравнений может быть записана так:

Рисунок 5.5 . – Неразрезная балка

Рисунок 5.6 . – Рациональный вариант выбора основной системы

Уравнения совместности перемещений называются канониче­скими уравнениями метода сил, поскольку они записываются по определенному закону (канону). Эти уравнения, количество ко­торых равно числу лишних неизвестных, совместно с уравнениями равновесия позволяют раскрыть статическую неопределимость системы, т. е. определить значения лишних неизвестных. Неиз­вестными в них являются реакции отброшенных связей Х₁ Х₂, Х₃ и т. д. (рис 5.5, б). В качестве коэффициентов при неизвестных стоят перемещения основной системы, вызванные единичными силами, действующими по на­правлению неизвестных (рис. 5.5, в—е), и внешней нагрузкой (рис. 5.5, ж).

Левые части уравне­ний выражают сум­марные перемещения точек приложения неизвестных сил по их направлениям от действия всех прило­женных сил. Поскольку эти перемещения отсутствуют, то правые части уравнений равны 0.

Канонические уравнения представляют собой систему линейных уравнений, решение которых не представляет принципиальных трудностей, однако при большом числе уравнений трудоемко. В первую очередь надо вычислить большое число перемещений. Коэффициенты при неизвестных образуют квадратную симметричную матрицу

.

В представленной матрице коэффициенты δ_ii называются главными перемещениями, а δ_ij (i ≠ j) — побочными. Главные перемещения, расположенные по диагонали матрицы, всегда положительны и не могут обратиться в нуль. Побочные перемещения, расположенные сим­метрично по отношению к диагонали матрицы, вследствие закона взаимности перемещений соответственно равны между собой. Побочные перемещения могут быть положительными, отрицательными или обращаться в нуль. Это свойство побочных перемещений дает возможность упрощать систему уравнений. Необходимо выбирать основную систему так, чтобы возможно большее число побочных перемещений обратилось в нуль.

При расчете статически неопределимых систем методом пере­мещений в качестве неизвестных принимаются угловые и ли­нейные перемещения узлов систем. Определив эти перемещения, можно найти соответствующие усилия, а затем выполнить обычное построение эпюр внутренних изгибающих моментов, продольных и поперечных сил.

В методе перемещений так же, как и в методе сил, выби­рается своя основная система, позволяющая легко строить эпюры, вызываемые всевозможными воздействиями. Но в отличие от метода сил основная система получается не устранением лишних связей, а добавлением новых дополнительных связей, которые препят­ствуют угловым и линейным перемещениям узлов исходной си­стемы.

В последнее время широкое распространение применительно к расчету инженерных конструкций (стержневых, листовых, обо­лочечных) получил метод конечных элементов (МКЭ), базирую­щийся на рассмотрении конструкции в виде совокупности отдель­ных конструктивных элементов, соединенных в конечном числе узловых точек. Другими словами, расчетная схема исходной (стержневой) конструкции представляется совокупностью ди­скретных элементов (стержней). В узловых точках прикладываются некоторые фиктивные усилия взаимодействия, определяющие действие внутренних напряжений.

Каждому узловому перемещению (линейному или угловому) соответствует узловое усилие. Совокупность этих усилий опре­деляет влияние смежных элементов (стержней) конструкции на рассматриваемый элемент.

Упругие свойства отдельных стержней, на которые разби­ваются конструкции, определяются их матрицей податливости или матрицей жесткости. Эти матрицы определяют связь между узловыми усилиями и узловыми перемещениями рассматривае­мого конечного элемента.

Расчет методом конечных элементов предполагает использование ЭВМ.

Определение перемещений упругих систем.

Для определения перемещений δ_ij и Δ_jp целесообразно воспользоваться формулой Мора. Она позволяет определять перемещения любых плоских геометрически неизменяемых и линейно деформируемых стержневых систем (балок, рам, ферм и т. п.).

Например, требуется определить перемещение какой-либо точки к рам­ной системы, вызванное приложенной к ней нагрузкой (рис. 5.7).

Рисунок 5.7 . – Определение перемещений упругих систем

Рассмотрим систему в двух со­стояниях. В первом (действи­тельном) состоянии система нагружается заданной нагруз­кой (рис. 5.7, а), а во втором (вспомогательном) — к системе в точке к приложена лишь одна внешняя единичная сила Р_к, по направлению которой и определяется искомое переме­щение Δ₂₁ (рис. 5.7, б).

Согласно формуле Мора:

Здесь буквами N, Q и M с соответствующими индексами обозначены продольная и поперечная силы и изгибающий момент в произвольном сечении конструкции, Е, G и μ – модуль Юнга, модуль сдвига и коэффициент Пуассона материала конструкции, F и J – площадь поперечного сечения и момент инерции сечения.

Следует заметить, что усилия N₁ , N_Р , М₁, М_Р, Q₁, Q_Р обычно представляют собой не фиксированные значения, а являются функ­циями координаты s, т. е. являются соответству­ющими эпюрами. При сопоставлении размерностей левой и пра­вой частей формулы Мора следует помнить, что в левой части перемещение Δ₂₁умножено на единицу силы.

При определении перемещений различных стержневых систем не все внутренние усилия целесообразно учитывать. Например, для перемещений в системах балочного и рамного типов, за исклю­чением коротких элементов большого сечения, поперечные и осе­вые силы не имеют существенного значения и ими можно пре­небречь. Поэтому в подавляющем числе случаев при определении перемещений в балках и рамах можно ограничиться работой внутренних сил только от изгибающих моментов, т. е. принимать один член в формуле Мора. Тогда

Для ферм, где стержни испытывают лишь осевые усилия, можно пренебречь влиянием М и Q. Поскольку по длине каждого стержня фермы осевые N₁ и N_Р и площади сечений F по­стоянны, можно вынести за знак интеграла N₁ , N_Р, F, а интеграл от ds равен длине стержня l. Тогда

(5.1)

5.5 Учет влияния изменения температуры
и неточностей изготовления и монтажа конструкций

Канонические уравнения для расчета статически неопредели­мых систем от действия изменения температуры на Δt отличаются от канонических уравнений при действии внешней нагрузки тем, что свободные члены Δ_1Р . Δ _пР и т. д. заменяются перемещениями Δ_1t . Δ _пt и т. д., представляющими собой температурные перемещения в основной системе по направлению лишних неизвестных Х₁ Х₂, . Х_п .

Перемещения , … имеют те же значения, что и при расчете на внешнюю нагрузку, а урав­нения имеют следующий вид:

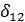
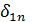
где — перемещение в основной системе от действия изменения температуры по направлению неизвестного Х_k.

Рассмотрим определение усилий, возникающих в портале в результате линейного перемещения его верхнего строения при изменении температуры на Δt (рис. 5.8, а).

Рисунок 5.8 . – Портал при изменении температуры на Δt

Каноническое уравнение будет иметь вид

,

откуда Х₁ = ,

где , если положительно, так как направлено в сторону, обратную . Здесь — коэффициент линейного расширения. Перемещение (рис. 5.8,б)

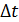
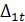
где .

Тогда неизвестная реакция в опоре от нагрева портала на температуру будет равна

Х₁ =

Канонические уравнения при расчете статически неопределимых систем с учетом неточностей монтажа опор имеют отличие лишь в том, что свободные члены Δ_1Р . Δ _пР и т. д. заменяются перемещениями Δ_1ос . Δ _пос и т. д., представляющими собой перемещения по направлению лишних неизвестных, вызванные осадкой опор. Канонические уравнения будут иметь следующий вид:

Рассмотрим в качестве примера трехопорную балку, у которой в процессе монтажа у средней опоры был допущен зазор Δ (рис. 5.9).

Рисунок 5.9 . — Трехпролетная балка с зазором у средней опоры

Каноническое уравнение будет иметь вид

Как известно,

С учетом зазора в данном случае ,

где

Если Δ = 0, то Х₁ = 5ql / 8.

Если Δ ≥ 5ql 4 / 384EJ, то Х₁ = 0.

Изгибающий момент в середине пролета

M_o,5l = ql 2 / 8 – X₁ l / 4 = ql 2 / 8 – 5ql 2 / 32 + 12ΔEJ / l 2 .

Изгибающий момент из-за зазора

ΔM ‘ = 12ΔEJ / l 2 = 6ΔEWh / l 2 ,

где h – высота сечения балки. Обусловленные наличием зазора напряжения в сечении балки, расположенном в середине пролета,

Принимая Е = 200000 МПа, Δ / l = 1/1000 и h / l = 1/20, получаем, что σ = 60 МПа (для сравнения предел текучести для проката из стали Ст.3 205-255 МПа).

🌟 Видео

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Ионные уравнения реакций. Как составлять полные и сокращенные уравненияСкачать

Лекция №1 Постановка задачи теории упругости. Условия совместности деформаций Сен-Венана.Скачать

Перемещения при изгибе. Часть 2. Непосредственное интегрирование уравнения изогнутой осиСкачать

Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Расчёт статически неопределимой рамы методом перемещенийСкачать

Математика это не ИсламСкачать

Лекция 8 Принцип возможных перемещенийСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Метод начальных параметров Расчет перемещений сечений балкиСкачать

СопроМат часть 1 Лекция 5 Растяжение сжатие статически неопределимых системСкачать

Основы метода конечных элементов. Часть 3. Основные уравнения теории упругости в МКЭСкачать