//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
- Калькулятор онлайн. Решение неравенств: линейные, квадратные и дробные.
- Немного теории.
- Числовые неравенства
- Решение неравенств второй степени с одной переменной
- Решение неравенств методом интервалов
- Решение линейных неравенств
- Основные понятия
- Типы неравенств
- Линейные неравенства: свойства и правила
- Правила линейных неравенств
- Решение линейных неравенств
- Равносильные преобразования
- Метод интервалов
- Графический способ
- Неравенства. Виды неравенств
- Неравенства – выражения вида (a>b), (a 5).
- Виды неравенств:
- Что такое решение неравенства?
- Если данное значение для икса превращает исходное неравенство верное числовое, то оно называется решением неравенства. Если же нет — то данное значение решением не является. И чтобы решить неравенство – нужно найти все его решения (или показать, что их нет).
- Когда в неравенстве меняется знак?
- При умножении (или делении) неравенства на отрицательное число, знак сравнения меняется на противоположный («больше» на «меньше», «больше или равно» на «меньше или равно» и так далее)
- Неравенства и ОДЗ
- 💥 Видео
Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Калькулятор онлайн.
Решение неравенств: линейные, квадратные и дробные.
Программа решения неравенств не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Причём, если в процессе решения неравенства нужно решить, например, квадратное уравнение, то его подробное решение также выводится (оно заключается в спойлер).
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5y +1/7y^2
Результат: ( 3frac — 5frac y + fracy^2 )
При вводе выражений можно использовать скобки. В этом случае при решении неравенства выражения сначала упрощаются.
Например: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)
Нажмите на кнопку 
Выберите нужный знак неравенства и введите многочлены в поля ниже.
Решить неравенство
Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Немного теории.
Сравнивать величины и количества при решении практических задач приходилось ещё с древних времён. Тогда же появились и такие слова, как больше и меньше, выше и ниже, легче и тяжелее, тише и громче, дешевле и дороже и т.д., обозначающие результаты сравнения однородных величин.
Понятия больше и меньше возникли в связи со счётом предметов, измерением и сравнением величин. Например, математики Древней Греции знали, что сторона любого треугольника меньше суммы двух других сторон и что против большего угла в треугольнике лежит большая сторона. Архимед, занимаясь вычислением длины окружности, установил, что периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых диаметра.
Символически записывать соотношения между числами и величинами с помощью знаков > и b. Записи, в которых два числа соединены одним из знаков: > (больше), frac ) верное числовое неравенство, 0,23 > 0,235 — неверное числовое неравенство.
Неравенства, в которые входят неизвестные, могут быть верными при одних значениях неизвестных и неверными при других. Например, неравенство 2x+1>5 верное при х = 3, а при х = -3 — неверное. Для неравенства с одним неизвестным можно поставить задачу: решить неравенство. Задачи решения неравенств на практике ставятся и решаются не реже, чем задачи решения уравнений. Например, многие экономические проблемы сводятся к исследованию и решению систем линейных неравенств. Во многих разделах математики неравенства встречаются чаще, чем уравнения.
Некоторые неравенства служат единственным вспомогательным средством, позволяющим доказать или опровергнуть существование определённого объекта, например, корня уравнения.
Далее вы узнаете свойства неравенств, научитесь решать неравенства. Полученные умения вам понадобятся при изучении последующего материала, для решения практических задач, а также задач физики и геометрии.
Видео:4 класс, 3 урок, Знаки "больше или равно" и "меньше или равно"Скачать

Числовые неравенства
Вы умеете сравнивать целые числа, десятичные дроби. Знаете правила сравнения обыкновенных дробей с одинаковыми знаменателями, но разными числителями; с одинаковыми числителями, но разными знаменателями. Здесь вы научитесь сравнивать любые два числа с помощью нахождения знака их разности.
Сравнение чисел широко применяется на практике. Например, экономист сравнивает плановые показатели с фактическими, врач сравнивает температуру больного с нормальной, токарь сравнивает размеры вытачиваемой детали с эталоном. Во всех таких случаях сравниваются некоторые числа. В результате сравнения чисел возникают числовые неравенства.
Определение. Число а больше числа b, если разность а-b положительна. Число а меньше числа b, если разность а-b отрицательна.
Если а больше b, то пишут: а > b; если а меньше b, то пишут: а b означает, что разность а — b положительна, т.е. а — b > 0. Неравенство а b, a = b, a , = или b и b > с, то а > с.
Теорема. Если к обеим частям неравенства прибавить одно и то же число, то знак неравенства не изменится.
Следствие. Любое слагаемое можно перенести из одной части неравенства в другую, изменив знак этого слагаемого на противоположный.
Теорема. Если обе части неравенства умножить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Следствие. Если обе части неравенства разделить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Вы знаете, что числовые равенства можно почленно складывать и умножать. Далее вы научитесь выполнять аналогичные действия с неравенствами. Умения почленно складывать и умножать неравенства часто применяются на практике. Эти действия помогают решать задачи оценивания и сравнения значений выражений.
При решении различных задач часто приходится складывать или умножать почленно левые и правые части неравенств. При этом иногда говорят, что неравенства складываются или умножаются. Например, если турист прошёл в первый день более 20 км, а во второй — более 25 км, то можно утверждать, что за два дня он прошёл более 45 км. Точно так же если длина прямоугольника меньше 13 см, а ширина меньше 5 см, то можно утверждать, что площадь этого прямоугольника меньше 65 см2.
При рассмотрении этих примеров применялись следующие теоремы о сложении и умножении неравенств:
Теорема. При сложении неравенств одинакового знака получается неравенство того же знака: если а > b и c > d, то a + c > b + d.
Теорема. При умножении неравенств одинакового знака, у которых левые и правые части положительны, получается неравенство того же знака: если а > b, c > d и а, b, с, d — положительные числа, то ac > bd.
Неравенства со знаком > (больше) и 1/2, 3/4 b, c и и b, quad ax
Видео:Решение квадратных неравенств | МатематикаСкачать

Решение неравенств второй степени с одной переменной
Неравенства вида
( ax^2+bx+c >0 ) и ( ax^2+bx+c 0 ) или ( ax^2+bx+c 0 или вниз при a 0 или в нижней при a 0 ) ) или ниже оси x (если решают неравенство
( ax^2+bx+c
Видео:Математика. Знаки больше, меньше, равно.Скачать

Решение неравенств методом интервалов
Рассмотрим функцию
f(x) = (х + 2)(х — 3)(х — 5)
Областью определения этой функции является множество всех чисел. Нулями функции служат числа -2, 3, 5. Они разбивают область определения функции на промежутки ( (-infty; -2), ; (-2; 3), ; (3; 5) ) и ( (5; +infty) )
Выясним, каковы знаки этой функции в каждом из указанных промежутков.
Выражение (х + 2)(х — 3)(х — 5) представляет собой произведение трех множителей. Знак каждого из этих множителей в рассматриваемых промежутках указан в таблице:
| ( (-infty; -2) ) | ( (-2; 3) ) | ( (3; 5) ) | ( (5; +infty) ) | |
| x+2 | – | + | + | + |
| x-3 | – | – | + | + |
| x-5 | – | – | – | + |
Отсюда ясно, что:
если ( x in (-infty;-2) ), то f(x) 0;
если ( x in (3;5) ), то f(x) 0.
Мы видим, что в каждом из промежутков ( (-infty; -2), ; (-2; 3), ; (3; 5), ; (5; +infty) ) функция сохраняет знак, а при переходе через точки -2, 3 и 5 ее знак изменяется.
| -2 | 3 | 5 |
Вообще пусть функция задана формулой
f(x) = (x-x1)(x-x2) . (x-xn),
где x–переменная, а x1, x2, . xn – не равные друг другу числа. Числа x1, x2, . xn являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль ее знак изменяется.
| -4 | 0 | 0,5 |
Выбираем те промежутки, на которых функция меньше нуля и записываем ответ.
Ответ:
( x in left( -4; ; 0 right) cup left( 0,5; ; +infty right) )
или
( -4 0,5 )
Наносим на числовую ось нули и точки разрыва функции:
Выбираем те промежутки, на которых функция меньше или равна нулю и записываем ответ.
Ответ:
( x in left( -infty; ; 1 right) cup left[ 4; ; +infty right) )
или
( x
Видео:Решение неравенства методом интерваловСкачать

Решение линейных неравенств
О чем эта статья:
Видео:Математика 1 класс (Урок№11 - Равенство. Неравенство. Знаки «больше», «меньше», «=».)Скачать

Основные понятия
Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.
Неравенство — это алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Линейные неравенства — это неравенства вида:
где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти все значения переменной, при которой неравенство верное.
Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Типы неравенств
- Строгие — используют только больше (>) или меньше ( b — это значит, что a больше, чем b.
- a > b и b > и
Видео:Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

Линейные неравенства: свойства и правила
Вспомним свойства числовых неравенств:
- Если а > b , то b а.
- Если а > b и b > c, то а > c. И также если а b, то а + c > b+ c (и а – c > b – c).
Если же а b и c > d, то а + c > b + d.
Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а d, то а – c b, m — положительное число, то mа > mb и
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
Если же а > b, n — отрицательное число, то nа
Обе части можно умножить или разделить на одно отрицательное число, при этом знак неравенства поменять на противоположный.
- Если а > b и c > d, где а, b, c, d > 0, то аc > bd.
Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>
Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.
Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.
Свойства выше помогут нам использовать следующие правила.
Видео:Математика. "Знаки "больше или равно" и "меньше или равно" (по Петерсон Л.Г.).Скачать

Правила линейных неравенств
- Любой член можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется.
- 2x − 3 > 6 ⇒ 2x > 6 + 3 ⇒ 2x > 9.
- Обе части можно умножить или разделить на одно положительное число. Знак неравенства при этом не меняется.
- Умножим обе части на пять 2x > 9 ⇒ 10x > 45.
- Обе части можно умножить или разделить на одно отрицательное число. Знак неравенства при этом меняется на противоположный.
- Разделим обе части на минус два 2x > 9 ⇒ 2x : (–2) > 9 : (–2) ⇒ x
Видео:Неравенства с модулем | Математика | TutorOnlineСкачать
Решение линейных неравенств
Линейные неравенства с одной переменной x выглядят так:
где a и b — действительные числа. А на месте x может быть обычное число.
Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать
Равносильные преобразования
Для решения ax + b , ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.
Алгоритм решения ax + b , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.
Рассмотрим пример: 0 * x + 5 > 0.
Как решаем:
- Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
- Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.
Видео:Математика 2 класс. 28 сентября. Меньше большеСкачать
Метод интервалов
Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.
Метод интервалов заключается в следующем:
- вводим функцию y = ax + b;
- ищем нули для разбиения области определения на промежутки;
- отмечаем полученные корни на координатной прямой;
- определяем знаки и отмечаем их на интервалах.
Алгоритм решения ax + b , ≥) при a ≠ 0 с использованием метода интервалов:
- найдем нули функции y = ax + b для решения уравнения ax + b = 0.
Если a ≠ 0, тогда решением будет единственный корень — х₀;
- начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
- определим знаки функции y = ax + b на промежутках.
Для этого найдем значения функции в точках на промежутке;
- если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если 0.
Как решаем:
В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,
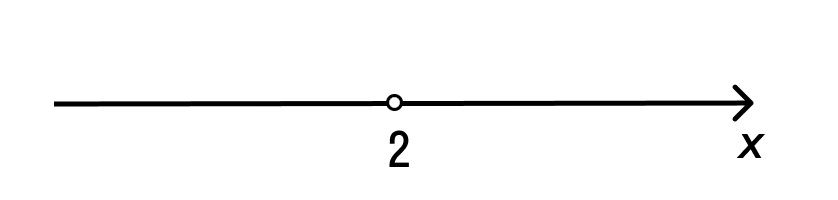
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
Определим знаки на промежутках.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.
Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6
Видео:Решение квадратных неравенств методом интервалов. 8 класс.Скачать
Графический способ
Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.
Алгоритм решения y = ax + b графическим способом
- во время решения ax + b 0 определить промежуток, где график изображается выше Ох;
- во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.
Рассмотрим пример: −5 * x − √3 > 0.
Как решаем
- Так как коэффициент при x отрицательный, данная прямая является убывающей.
- Координаты точки пересечения с Ох равны (−√3 : 5; 0).
- Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
- Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.
Ответ: (−∞, −√3 : 5) или x
Видео:Знак Больше Меньше Равно / Математика / 1 класс / Сравнение чисел / Развивающие МУЛЬТИКИ для детейСкачать
Неравенства. Виды неравенств
Неравенства – выражения вида (a>b), (a 5).
Видео:Как решить неравенства с модулем?Скачать
Виды неравенств:
Если (a) и (b) – это числа или числовые выражения , то неравенство называется числовым. Фактически это просто сравнение двух чисел. Такие неравенства подразделяются на верные и неверные.
Переменная только в первой степени
Есть переменная во второй степени (квадрате), но нет старших степеней (третьей, четвертой и т.д.)
Есть переменная под знаком логарифма
. и так далее.
Также неравенства подразделяются на строгие и нестрогие — подробнее смотри здесь .
Видео:Знаки неравенства (больше, меньше)Скачать
Что такое решение неравенства?
Если в неравенство вместо переменной подставить какое-нибудь число, то оно превратится в числовое.
Если данное значение для икса превращает исходное неравенство верное числовое, то оно называется решением неравенства. Если же нет — то данное значение решением не является. И чтобы решить неравенство – нужно найти все его решения (или показать, что их нет).
Например, если мы в линейное неравенство (x+6>10), подставим вместо икса число (7) –получим верное числовое неравенство: (13>10). А если подставим (2), будет неверное числовое неравенство (8>10). То есть (7) – это решение исходного неравенства, а (2) – нет.
Однако, неравенство (x+6>10) имеет и другие решения. Действительно, мы получим верные числовые неравенства при подстановке и (5), и (12), и (138). И как же нам найти все возможные решения? Для этого используют равносильные преобразования неравенств . Для нашего случая имеем:
То есть нам подойдет любое число больше четырех. Теперь нужно записать ответ. Решения неравенств, как правило, записывают числовыми промежутками , дополнительно отмечая их на числовой оси штриховкой. Для нашего случая имеем:
Видео:Знаки больше и меньше. Или один знак?Скачать
Когда в неравенстве меняется знак?
В неравенствах есть одна большая ловушка, в которую очень «любят» попадаться ученики:
При умножении (или делении) неравенства на отрицательное число, знак сравнения меняется на противоположный («больше» на «меньше», «больше или равно» на «меньше или равно» и так далее)
Почему так происходит? Чтобы это понять, давайте посмотрим преобразования числового неравенства (3>1). Оно верное, тройка действительно больше единицы. Сначала попробуем умножить его на любое положительное число, например, двойку:
Как видим, после умножения неравенство осталось верным. И на какое бы положительное число мы не умножали – всегда будем получать верное неравенство. А теперь попробуем умножить на отрицательное число, например, минус тройку:
Отметим на оси числовой промежуток. Неравенство строгое , поэтому само значение (-1) «выкалываем» и в ответ не берем
Запишем ответ в виде интервала
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
Неравенства и ОДЗ
Неравенства, также как и уравнения могут иметь ограничения на область допустимых значений , то есть на значения икса. Соответственно, из промежутка решений должны быть исключены те значения, которые недопустимы по ОДЗ.
(x+1 дробно-рациональных , иррациональных (как в примере выше) и логарифмических неравенствах , а также тригонометрических неравенствах, содержащих переменную под функцией тангенса или котангенса. Какие ограничения при этом накладываются, вы можете посмотреть здесь .
💥 Видео
Решение системы неравенствСкачать