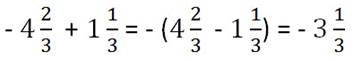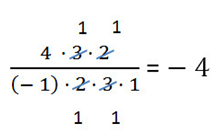Уравнения с отрицательными и положительными числами за 6 класс (3 видео)

Уравнения с отрицательными и положительными числами за 6 класс

Математику уж затем учить надо, что она ум в порядок приводит

Содержание

Основные правила математики с примерами. 6 класс. Часть 2.
Содержание
СПРАВОЧНЫЙ МАТЕРИАЛ по теме: «Уравнения, свойства уравнений. Решение задач с помощью уравнений» 6 класс
Памятка по теме «Решение уравнений» (6 класс)
Просмотр содержимого документа «Памятка по теме «Решение уравнений» (6 класс)»
—>Школа математики для всех, кто учиться и преподает —>
Каталог статей
🎥 Видео

Основные правила математики с примерами. 6 класс. Часть 2.

Содержание

Умножение. Свойства умножения

Произведением числа на натуральное число не равное 1, называют сумму, состоящую из слагаемых, каждое из которых равно а:

a · b = a + a + a + . . . + a ⏟ b

Если один из двух множителей равен 1, то произведение равно второму множителю:

Если один из множителей равен нулю, то произведение равно нулю:

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

!Важное правило. Помогает решать уравнения

( x — a ) ( x — b ) = 0 ; И л и x — a = 0 , и л и x — b = 0 ; 2 к о р н я x = a и x = b . ( x — 5 ) ( x + 2 ) = 0 ; И л и x — 5 = 0 , и л и x + 2 = 0 ; 2 к о р н я x = 5 и x = — 2 .

Умножение обыкновенных дробей

Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:

Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Умножение рациональных чисел

Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».

Чтобы умножить два отрицательных числа, надо умножить их модули.

Для любого рационального числа :

Если произведение • — отрицательное, то числа и имеют разные знаки.

Деление обыкновенных дробей

Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:

a b : c d = a b · d c

Деление рациональных чисел

Чтобы найти частное двух чисел с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».

Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.

Нахождение дроби от числа

Чтобы найти дробь от числа, можно число умножить на эту дробь.

Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.

Нахождение числа по его дроби

Чтобы найти число по значению его дроби, можно это значение разделить на эту дробь.

Найти число, если известно, что

е г о д р о б ь 5 7 с о с т а в л я е т ч и с л о 15 : 15 : 5 7 = 15 · 7 5 = 15 3 · 7 5 1 = 21

Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.

Найти число, если известно, что

24 % э т о г о ч и с л а р а в н ы 48 . 24 % = 24 100 ; 48 : 24 100 = 48 · 100 24 = 48 2 · 100 24 1 = 200

Степень числа

Степенью числа с натуральным показателем , большим , называют произведение множителей, каждый из которых равен :

a n = a · a · a · … · a ⏟ n

Число при этом называют основанием степени.

Степенью числа с показателем называют само число

Вторую степень числа называют также квадратом числа. Например, запись читают: « в квадрате».
Третью степень называют кубом числа, а запись читают: « в кубе».

Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а затем производят другие действия.

Найти значение выражения

5 · 2 3 + 15 5 · 2 2 3 1 + 3 15 = 5 · 8 + 15 = 40 + 15 = 55

Числовые и буквенные выражения

Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением.

Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.

Приведение подобных слагаемых

Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.

Раскрытие скобок

Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.

Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.

Свойства уравнений

Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.

Если данное уравнение не имеет корней, то, прибавив к обеим его частям одно и то же число, получим уравнение, тоже не имеющее корней.

Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.

Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.

Отношения

Частное двух чисел и , не равных нулю, еще называют отношением чисел и , или отношением числа к числу .

Отношение положительных чисел и показывает, во сколько раз число больше числа , или какую часть число составляет число .

показывает, что число 10 в 5 раз больше числа 2 или число 2 в 5 раз меньше числа 10.

Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Пропорции

Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:

a : b = c : d и л и a b = c d

Числа и называют крайними членами пропорции, а числа и — средними членами пропорции.

Основное свойство пропорции

Произведение крайних членов пропорции равно произведению ее средних членов:

a b = c d ⇒ a d = b c

Если , , и числа, не равные нулю, и • = • , то отношения

могут образовывать пропорцию

Процентное отношение двух чисел

Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

Прямая и обратная пропорциональная зависимость

Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

Если величины и обратно пропорциональны, то их соответствующие значения удовлетворяют равенству

, где -число, постоянное для данных величин.

Видео:Решение уравнений с отрицательными числами.Скачать

СПРАВОЧНЫЙ МАТЕРИАЛ по теме: «Уравнения, свойства уравнений. Решение задач с помощью уравнений» 6 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

Свидетельства для портфолио
Вечный доступ за 120 рублей
311 видеолекции для каждого

1. Правила действий с рациональными числами

Чтобы сложить два отрицательных числа, надо сложить их модули и перед результатом поставить знак «-» (минус).

Чтобы сложить положительное и отрицательное число, надо найти разность их модулей и перед результатом поставить знак числа с большим модулем.

Чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.

Вычитание рациональных чисел всегда можно заменить сложением:

Чтобы умножить отрицательное число и положительное, надо умножить их модули и перед результатом поставить знак минус: (- a )* b =- ab .

Чтобы умножить два отрицательных числа, надо умножить их модули: (- a )*(- b )= ab .

Чтобы разделить одно рациональное число на другое, надо разделить их модули; если знаки делимого и делителя разные, то перед результатом нужно поставить знак минус.

Д) возведение в степень:

и т.д.

Е) порядок выполнения действий

Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а потом действия в скобках (если есть), умножение или деление по порядку, сложение, вычитание по порядку.

2. Правило нахождения дроби от числа

Чтобы найти дробь от числа, надо число умножить на эту дробь.

от а равно а*.

от 200 равно 200*=80.

3. Правило нахождения числа по значению дроби

Чтобы найти число по значению дроби, надо значение дроби разделить на эту дробь.

Если от х равно с, то х=с: .

Если от числа равно 80, то число равно 80: =200.

4. Условие равенства нулю произведения

Произведение нескольких множителей равно нулю, если хотя бы один из множителей равен нулю.

a * b =0, если а=0 или b =0 или а= b =0.

5. Определение модуля числа

Модулем числа а называется расстояние в единичных отрезках от начала координат до точки с координатой а.

—4 4

6. Правило нахождения модуля числа

Модулем неотрицательного числа является само число, модулем отрицательного числа является противоположное ему число.

А (-2) 0 В(3)

а, если число а неотрицательное;

-а, если число а отрицательное.

7. Среднее арифметическое

Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на количество слагаемых.

8. Определение пропорции

Пропорция – это равенство двух отношений a : b = c : d или при

a и d – крайние члены пропорции, b и c – средние члены пропорции.

9. Основное свойство пропорции

Произведение крайних членов верной пропорции равно произведению ёё средних членов

Если 0,3:1=2,1:7, то 0,3*7=1*2,1.

10. Правило нахождения членов пропорции

Чтобы найти неизвестный крайний член пропорции, достаточно произведение ёё крайних членов разделить на известный крайний. Чтобы найти неизвестный средний член пропорции, достаточно произведение её крайних членов разделить на известный средний.

А) ;

;

В)

11. Процент и процентное отношение

Один процент — это одна сотая часть.

1%=0,01; 100%=1; 50%=0,5; 200%=2.

Процентное отношение — это отношение двух чисел, выраженное в процентах.

А) Пример: отношение 2 к 5 равно

Б) задача. Возле школы растёт 20 деревьев, из них 8 – липы. Сколько процентов этих деревьев составляют липы?

Отношение лип ко всем деревьям возле школы равно или 0,4 или 40%. Таким образом, липы составляют 40% всех деревьев, растущих возле школы.

12. Основные задачи на проценты

1. нахождение процентов от числа;

2. нахождение числа по процентам;

3. нахождение процентного отношения двух чисел.

Примеры задач (их можно решить несколькими способами)

Надо вспахать поле, площадь которого равна 300 га. В первый день трактористы выполнили 40% задания. Сколько гектаров они вспахали в первый день?

Решение (способ подстановки)

300 га – 100%

Значит, в первый день вспахали 120 га.

В первый день трактористы вспахали 120 га, что составляет 40% всего поля. Найдите площадь всего поля.

120 га – 40%

Значит, площадь всего поля 300 га.

Надо вспахать поле, площадь которого равна 300 га. В первый день трактористы вспахали 120 га. Сколько процентов всего поля они вспахали в первый день?

300 га – 100%

Значит, в первый день они вспахали 40%.

13. Преобразование простейших выражений

1) Правила раскрытия скобок

А) перед которыми стоит знак «+».

Чтобы раскрыть в выражении скобки, перед которыми стоит знак «+», достаточно опустить скобки и знак перед ними.

2а + ( x — y + z )=2 a + x — y + z

Б) перед которыми стоит знак «-»

Чтобы раскрыть в выражении скобки, перед которыми стоит знак «-», достаточно опустить скобки и знак перед ними, а знаки слагаемых, которые были в скобках, изменить на противоположные: +(а — с)=а-с; -(а — с)=-а+с.

В) с помощью распределительного свойства умножения:

5*(х+2 y -0,5 t )=5 x +10 y -0,25 t .

Приведение подобных слагаемых

А) определение подобных слагаемых

Слагаемые, отличающиеся только числовым множителем, называются подобными.

5х, -3х, 2х – подобные;

Б) Правило приведения подобных слагаемых

Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общий буквенный множитель.

II . Уравнения. Повторение

14. Определение уравнения

Уравнение – это равенство, которое содержит неизвестные числа, обозначенные буквами (значения которых надо найти).

15. Знак, который делит уравнение на левую и правую части – это знак «=».

6х-5 = 10

Левая часть правая часть

16. Определение корня уравнения

Корнем (или решением) уравнения называется то значение неизвестной, при котором уравнение превращается в верное равенство.

Для уравнения 2х+2=8

х=3 – корень уравнения, т.к. 2*3+2=8 = верно, а х=4 – не является корнем, т.к. 2*4+28.

17. Количество корней уравнения

Уравнение может иметь один корень, два, несколько или бесчисленное множество корней, а может совсем не иметь корней.

2х+7=1 имеет один корень — х=-3;

имеет два корня: ;

(х-3)(х-2)(х+1)=0 имеет три корня: ;

— не имеет корней;

— бесконечное множество корней.

18. Что значит решить уравнение

Решить уравнение — означает найти все его корни или убедиться, что их вообще нет.

19. Решение уравнений с помощью правил нахождения количества действий

А) неизвестного слагаемого

Чтобы найти неизвестно слагаемое, надо из суммы вычесть известное слагаемое.

Пример. Решите уравнение 78+х=100

Б) неизвестного вычитаемого

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Пример. Решите уравнение 108-х=96.

В) неизвестного уменьшаемого

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Пример. Решите уравнение х-34=32.

Г) неизвестного множителя

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Пример. Решите уравнение 5х=15.

Д) неизвестного делимого

Чтобы найти неизвестное делимое, надо делитель умножить на частное.

Пример. Решите уравнение х:21=16.

Е) неизвестного делителя

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Пример. Решите уравнение 576:х=18.

III . Решение уравнений

20. Определение равносильных уравнений

Два уравнения называются равносильными, если каждое из них имеет те же корни, что и другое. Равносильными считают и те уравнение, которые не имеют корней.

21. Действия, позволяющие заменить данное уравнение равносильным ему

А) преобразование выражений (см. 13);

Б) Применение основных свойств уравнений (см. 22);

22. Основные свойства уравнений

А) о переносе слагаемых из одной части уравнения в другую

Любое слагаемое можно перенести из одной части уравнения в другую, изменив его знак на противоположный. При этом получим уравнение, равносильное данному.

5х=21-2х и 5х+2х=21 имеют одни и те же корни.

Б) об умножении или делении обеих частей уравнения на одно и то же число, не равное нулю.

Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получим уравнение, которое имеет те же корни, что и данное.

Пример. Решить уравнение .

Умножим обе части уравнения на 4:

2х=-3-х;

23. В чём заключается процесс решения уравнений

Процесс решения уравнений – это замена данного уравнения более простым уравнением, равносильным данному, которое мы получаем, используя (тождественные) преобразования выражений и свойства уравнений.

IV Определенные правила, используемые при решении задач на составление уравнения

24. Правило 1. Если в задаче несколько неизвестных, то обозначаем буквой х меньшее из них, либо то, с которым сравниваются остальные неизвестные.

1) Пример. Задача 1. В одной корзине в 3 раза меньше яблок, чем в другой, а вместе в двух корзинах 28 кг. Сколько килограммов яблок в каждой корзине?

Можно записать сначала условие как в младших классах, а затем обозначить неизвестные.

1 — ? кг, в 3 р.

х кг

Если обозначить наоборот:

1 — ? кг, в 3 р.

х:3 кг

то получаем уравнение , которое решить труднее, чем уравнение х+3х=28.

2) Задача 2. В трёх цехах завода 115 рабочих. В 1 цехе в 2 раза больше, чем во втором, а третьем на 5 меньше, чем во 2. Сколько рабочих в каждом цехе?

Решение

1 — ? раб., в 2 р. >

2 – ? раб. 115 раб.

2х раб.

25. Правило 2 . Если в задаче неизвестно, на сколько одна величина больше, чем другая, то составить уравнение можно, используя три способа.

Например, если число а больше числа b на 5, то это условие можно записать таким образом:

a-b=5 или a-5=b, или b+5=a.

Задача 3. В одном ящике было в 5 раз больше винограда, чем в другом. Сколько килограммов винограда было в каждом ящике, если во втором было на 40 кг меньше, чем в первом?

Правильно записанное короткое условие задачи даёт возможность легко составить уравнение.

1 — ? кг, в 5 р. > 5х кг

2 — ? кг х кг, на 40 кг

Значит, во втором ящике было 10 кг, а в первом 5*10=50 кг.

Ответ: 50 кг, 10 кг.

26. Правило 3. Если в задаче известно, во сколько раз одна величина меньше (больше), чем другая, то уравнение можно составить, используя три способа.

Например, если число а больше числа b в 5 раз, то это условие можно записать так: а=5 b или b =5: a , или b =1/5 a .

Очевидно, что лучшим является а=5 b . Если из двух величин меньшую обозначить х, то большая будет равна 5х.

Задача 4. Я на 6 лет старше своей сестры, а она моложе меня в 4 раза. Сколько лет мне и моей сестре?

Я – (х+6) лет

Сестра – х лет, в 4 раза

Значит, сестре 2 года, тогда мне 2+6=8 лет.

Ответ: 2 года, 8 лет.

27. Правило 4. Во время решения задач на движение нужно, чтобы единицы измерения были в одной системе (км/час, час, км). Следует обратить внимание на единицы измерения времени.

Например, 1 ч 12 мин=

V Типы задач и запись их условий

28. 1) Условие задач на движение удобно изображать с помощью схемы

2) Тип 1. Задачи на движение по суше

Задача 5. Расстояние между двумя городами автомобиль преодолевает за 1,5 часа, а мотоциклист за 2 часа. Найдите расстояние между городами, если скорость мотоциклиста на 18 км/ч меньше скорости автомобиля.

Условие можно записать в таблицу

х>0 . Полу чаем уравнение:

Значит, скорость мотоциклиста 54 км/ч, а расстояние между городами 2*54=108 км.

3) Тип 2. Задачи на движение по воде

В этих задачах есть собственная скорость катера (лодки и т.п.), которая должна быть больше скорости течения, и скорость течения. Тогда скорость катера и скорость течения. Тогда скорость катера

; (в озере стоячая вода)

Задача 6. Катер прошёл по реке от пристани А до пристани В и вернулся назад. От пристани А до пристани В катер шёл 2 часа. Через 2,5 часа после выхода катера от пристани В ему осталось пройти до пристани А ещё 3 км. Найдите расстояние между пристанями, если скорость течения реки 3 км/час.

Анализируем условие задачи. На путь о пристани А до В катер затратил меньше времени, чем на обратный путь, поэтому от пристани А до пристани В он шёл по течению реки. Запишем условие, обращая внимание на допустимые значения х.

, , тогда х> 3 .

А В (по теч.)

2(х+3)

В А (против теч.)

4) Тип 3. Задачи экономического содержания

Во время решения задач по теме «Цена, количество, стоимость» условие удобно записывать с помощью таблицы, выражая цену и стоимость в гривнях или в копейках.

Задача 7. За 7 тетрадей и 4 альбома для рисования заплптили 5 грн. 41 к. Сколько стоит одна тетрадь и одни альбом, если альбом дороже тетради на 72 к.?

5 грн. 41 к.=541 к.

Стоимость, к.

Получаем уравнение: 7х+ 4(х+2)=541.

5) Тип 4. Задачи геометрического содержания

Периметр: Р=( a + b )*2;

Площадь: S = a * b .

Площадь: S =.

Задача 8. Длина прямоугольника в 4 раза больше его ширины, а периметр равен 60 м. Найдите площадь прямоугольника.

Условие можно записать так:

S — ?

Площадь S =? ;

Значит, ширина прямоугольника 6м, а длина 4*6=24 м. Тогда площадь равна 6*24=144.

Ответ: 144.

Тип 5. Задачи «Было — стало» или «на переливание»

Задача 9. На одном складе было в 3 раза больше телевизоров, чем на другом. После того, как из первого склада взяли 20 телевизоров, а на другой привезли 14, на обоих складах стало поровну телевизоров. Сколько телевизоров было на каждом складе сначала?

Стало

Получаем уравнение: 3х-20=х+14.

7) Тип 6. Задачи на нахождение дроби от числа

Задача 10. Велосипедист проехал 5/7 запланированного пути и ещё 40 км, после чего ему осталось проехать 0,75 пути без 118 км. Какова длина всего пути?

С помощью схемы (см. рис) составим краткое условие задачи.

(5/7х+40)км (0,75х-118)км

1 часть — (5/7х+40)км;

2 часть — (0,75-118)км

Получаем уравнение: (5/7х+40)+ (0,75-118)=х.

8) Тип 7. Задачи на проценты

Задача 11. Кусок сплава меди, цинка и олова содержит 40% меди и 120 г олова. Найдите массу этого куска, если в нём цинка на 50 г меньше, чем меди.

Запишем проценты в виде дроби.

Медь – 0,4х г;

Получаем уравнение: 0,4х+(0,4х-50)+120=х.

9) Задачи повышенной сложности.

Задача 12 (сборник Сканави, №13.001). Из четырёх чисел первые три относятся как , а четвёртое составляет 15% второго. Найдите эти числа, если известно, что второе число больше суммы других на 8 единиц.

Рассмотрим отношения: . Значит, данные числа относятся как 6:10:1. Имеем:

Получаем уравнение: 10х-(6х+х+1,5х)=8.

Задача 13. (Сборник Сканави, 3 13.003). В двух баках 70 л воды. Если из первого бака перелить во второй 12,55 воды, вмещавшейся в нём, то в обоих баках воды станет поровну. Сколько литров воды в каждом баке?

Обратим внимание, что известна сумма. Обозначив через х количество воды в первом баке, будем иметь в другом баке (70-х)л.

Запишем условие в таблицу.

х — поровну

(70-х)+

Получаем уравнение: х-= (70-х)+ .

Задача 14. Цену товара снизили сначала на 20%¸ потом новую цену снизили ещё на 15% и в третий раз снизили цену товара ещё на 10%. На сколько процентов снизили первоначальную цену товара?

Была цена – х грн.

После первого снижение на 20% — 0,8х грн.

После второго снижения на 15% — 0,8х*0,85 грн.

После третьего снижения на 10% — 0,8х*0,85*0,9 грн.

Последняя цена составляет 0,8*0,85*0,9х=0,6120х=61,2%х.

Цена снизилась на 100% — 61,2%=38,8%.

29. Алгоритм решения уравнений

1. Избавиться от знаменателей

2. Раскрыть скобки

3. Перенести члены с переменными в левую часть уравнения,

а другие – в правую

4. Привести подобные слагаемые

30. Порядок выполнения действий в числовых выражениях

Видео:Уравнения с отрицательными числами (Математика 6 класс)Скачать

Памятка по теме «Решение уравнений» (6 класс)

В данном материале рассматривается тема «Решение уравнений» в 6 классе. Для более быстрого и успешного усвоения алгоритма решения уравнений я раздаю памятку каждому ученику.

Просмотр содержимого документа
«Памятка по теме «Решение уравнений» (6 класс)»

Шаг 1. Раскрыть скобки (если они есть), используя правила:

Правило 1. Если перед скобками стоит знак «плюс», то надо опустить эти скобки и этот знак «плюс», сохранив знаки у слагаемых, стоящих в скобках.

Правило 2. Если перед скобками стоит знак «минус», то надо опустить эти скобки и этот знак «минус», изменив знаки у слагаемых, стоящих в скобках, на противоположные.

Правило 3. Чтобы умножить положительное число на сумму, надо умножить это число на каждое слагаемое в сумме, сохранив знаки у слагаемых.

Правило 4. Чтобы умножить отрицательное число на сумму, надо умножить это число на каждое слагаемое в сумме, изменив знаки у слагаемых на противоположные.

Шаг 2. Привести подобные слагаемые (слагаемые, у которых одинаковая буквенная часть), используя правила:

Правило 1. Чтобы сложить два числа с одинаковыми знаками, надо:

поставить их общий знак;

сложить их модули.

Правило 2. Чтобы сложить два числа с разными знаками, надо:

поставить знак числа с бÓльшим модулем;

из бÓльшего модуля вычесть меньший.

Правило 3. Сумма двух противоположных чисел равна нуля.

Правило 4. От прибавления нуля число не изменяется.

Шаг 3. Перенести слагаемые из одной части уравнения в другую, изменив при этом их знак на противоположный. Слагаемые, содержащие неизвестное, собирают в левой части уравнения, числа – в правой части уравнения.

Шаг 4. Привести подобные слагаемые отдельно в левой части уравнения, отдельно в правой части уравнения.

Шаг 5. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель, используя правила:

Правило 1. Чтобы разделить два числа с одинаковыми знаками, надо:

поставить знак «плюс»;

модуль делимого разделить на модуль делителя.

Правило 2. Чтобы разделить два числа с разными знаками, надо:

поставить знак «минус»;

модуль делимого разделить на модуль делителя.

Правило 3. При делении нуля на любое число, не равное нулю, получается нуль.

Правило 4. Делить на нуль запрещено!

Видео:Сложение и вычитание рациональных чисел. 6 класс.Скачать

—>Школа математики для всех, кто учиться и преподает —>

Видео:Как вычитать отрицательные числа? / Простые примеры из жизни по математикеСкачать

Каталог статей

Положительные и отрицательные числа
Координатная прямая
Проведём прямую. Отметим на ней точку 0 (ноль) и примем эту точку за начало отсчёта.

Укажем стрелкой направление движения по прямой вправо от начала координат. В этом направлении от точки 0 будем откладывать положительные числа.

То есть положительными называют уже известные нам числа, кроме нуля.

Иногда положительные числа записывают со знаком «+». Например, «+8».

Для краткости записи знак «+» перед положительным числом обычно опускают и вместо «+8» пишут просто 8.

Поэтому «+3» и «3» — это одно и тоже число, только по разному обозначенное.

Выберем какой-либо отрезок, длину которого примем за единицу и отложим его несколько раз вправо от точки 0. В конце первого отрезка записывается число 1, в конце второго — число 2 и т.д.

Отложив единичный отрезок влево от начала отсчёта получим отрицательные числа: -1; -2; и т.д.

Отрицательные числа используют для обозначения различных величин, таких как: температура (ниже нуля), расход — то есть отрицательный доход, глубина — отрицательная высота и другие.

Как видно из рисунка, отрицательные числа — это уже известные нам числа, только со знаком «минус»: -8; -5,25 и т.д.

Число 0 не является ни положительным, ни отрицательным.

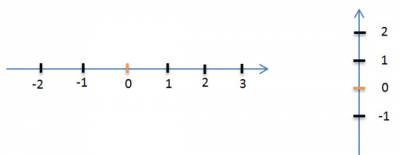
Числовую ось обычно располагают горизонтально или вертикально.

Если координатная прямая расположена вертикально, то направление вверх от начала отсчёта обычно считают положительным, а вниз от начала отсчёта — отрицательным.

Стрелкой указывают положительное направление.

Прямая, на которой отмечено:
• начало отсчёта (точка 0);
• единичный отрезок;
• стрелкой указано положительное направление;
называется координатной прямой или числовой осью.

Противоположные числа на координатной прямой
Отметим на координатной прямой две точки A и B, которые расположены на одинаковом расстоянии от точки 0 справа и слева соответственно.

В таком случае длины отрезков OA и OB одинаковы.

Значит, координаты точек A и B отличаются только знаком.

Также говорят, что точки A и B симметричны относительно начала координат.
Координата точки A положительная «+2», координата точки B имеет знак минус «-2».
A (+2), B (-2).

Числа, которые отличаются только знаком, называются противоположными числами. Соответствующие им точки числовой (координатной) оси симметричны относительны начала отсчёта.

Каждое число имеет единственное противоположное ему число. Только число 0 не имеет противоположного, но можно сказать, что оно противоположно самому себе.

Запись «-a» означает число, противоположное «a». Помните, что под буквой может скрываться как положительное число, так и отрицательное число.

Пример:
-3 — число противоположное числу 3.

Записываем в виде выражения:
-3 = -(+3)

Пример:
-(-6) — число противоположное отрицательному числу -6. Значит, -(-6) это положительное число 6.

Записываем в виде выражения:
-(-6) = 6

Сложение отрицательных чисел
Сложение положительных и отрицательных чисел можно разобрать с помощью числовой оси.

Сложение небольших по модулю чисел удобно выполнять на координатной прямой, мысленно представляя себе как точка, обозначающая число передвигается по числовой оси.

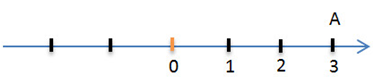
Возьмём какое-нибудь число, например, 3. Обозначим его на числовой оси точкой A.

Прибавим к числу положительное число 2. Это будет означать, что точку A надо переместить на два единичных отрезка в положительном направлении, то есть вправо . В результате мы получим точку B с координатой 5.
3 + (+ 2) = 5

Для того чтобы к положительному числу, например, к 3 прибавить отрицательное число (- 5), точку A надо переместить на 5 единиц длины в отрицательном направлении, то есть влево .

В этом случае координата точки B равна — 2.

Итак, порядок сложения рациональных чисел с помощью числовой оси будет следующим:
• отметить на координатной прямой точку A с координатой равной первому слагаемому;
• передвинуть её на расстояние, равное модулю второго слагаемого в направлении, которое соответствует знаку перед вторым числом (плюс — передвигаем вправо, минус — влево);
• полученная на оси точка B будет иметь координату, которая будет равна сумме данных чисел.

Двигаясь от точки — 2 влево (так как перед 6 стоит знак минус), получим — 8.
— 2 + (- 6) = — 8

Сложение чисел с одинаковыми знаками
Складывать рациональные числа можно проще, если использовать понятие модуля.

Пускай нам нужно сложить числа, которые имеют одинаковые знаки.
Для этого, отбрасываем знаки чисел и берём модули этих чисел. Сложим модули и перед суммой поставим знак, который был общим у данных чисел.

Пример.

Пример сложения отрицательных чисел.
(- 3,2) + (- 4,3) = — (3,2 + 4,3) = — 7,5

Чтобы сложить числа одного знака надо сложить их модули и поставить перед суммой знак, который был перед слагаемыми.

Сложение чисел с разными знаками
Если числа имеют разные знаки, то действуем несколько по-иному, чем при сложении чисел с одинаковыми знаками.
• Отбрасываем знаки перед числами, то есть берём их модули.
• Из большего модуля вычитаем меньший.
• Перед разностью ставим тот знак, который был у числа с бóльшим модулем.

Пример сложения отрицательного и положительного числа.
0,3 + (- 0,8) = — (0,8 — 0,3) = — 0,5

Пример сложения смешанных чисел.

Чтобы сложить числа разного знака надо:
• из бóльшего модуля вычесть меньший модуль;
• перед полученной разностью поставить знак числа, имеющего больший модуль.

Вычитание отрицательных чисел
Как известно вычитание — это действие, противоположное сложению.
Если a и b — положительные числа, то вычесть из числа a число b, значит найти такое число c, которое при сложении с числом b даёт число a.
a — b = с или с + b = a

Определение вычитания сохраняется для всех рациональных чисел. То есть вычитание положительных и отрицательных чисел можно заменить сложением.

Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.

Или по другому можно сказать, что вычитание числа b — это тоже самое сложение, но с числом противоположным числу b.
a — b = a + (- b)

Пример.
6 — 8 = 6 + (- 8) = — 2

Пример.
0 — 2 = 0 + (- 2) = — 2

Стоит запомнить выражения ниже.
0 — a = — a
a — 0 = a
a — a = 0

Правила вычитания отрицательных чисел
Как видно из примеров выше вычитание числа b — это сложение с числом противоположным числу b.
Это правило сохраняется не только при вычитании из бóльшего числа меньшего, но и позволяет из меньшего числа вычесть большее число, то есть всегда можно найти разность двух чисел.

Разность может быть положительным числом, отрицательным числом или числом ноль.

Примеры вычитания отрицательных и положительных чисел.
• — 3 — (+ 4) = — 3 + (- 4) = — 7
• — 6 — (- 7) = — 6 + (+ 7) = 1
• 5 — (- 3) = 5 + (+ 3) = 8
Удобно запомнить правило знаков, которое позволяет уменьшить количество скобок.
Знак «плюс» не изменяет знака числа, поэтому, если перед скобкой стоит плюс, то знак в скобках не меняется.
+ (+ a) = + a

Знак «минус» перед скобками меняет знак числа в скобках на противоположный.
— (+ a) = — a

Из равенств видно, что если перед и внутри скобок стоят одинаковые знаки, то получаем «+», а если знаки разные, то получаем «-».
(- 6) + (+ 2) — (- 10) — (- 1) + (- 7) = — 6 + 2 + 10 + 1 — 7 = — 13 + 13 = 0

Правило знаков сохраняется и в том случае, если в скобках не одно число, а алгебраическая сумма чисел.
a — (- b + c) + (d — k + n) = a + b — c + d — k + n

Обратите внимание, если в скобках стоит несколько чисел и перед скобками стоит знак «минус», то должны меняться знаки перед всемичислами в этих скобках.

Чтобы запомнить правило знаков можно составить таблицу определения знаков числа.
Правило знаков для чисел

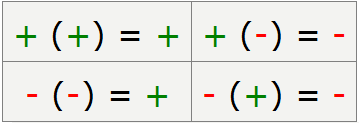
Или выучить простое правило.

Минус на минус даёт плюс,
Плюс на минус даёт минус.

Умножение отрицательных чисел
Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.

Умножение чисел с одинаковыми знаками
Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.
Чтобы умножить два числа с одинаковыми знаками надо:
• перемножить модули чисел;
• перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).

Примеры умножения отрицательных и положительных чисел.
• (- 3) • (- 6) = + 18 = 18
• 2 • 3 = 6

Умножение чисел с разными знаками
Второй возможный случай — это умножение чисел с разными знаками.
Чтобы умножить два числа с разными знаками, надо:
• перемножить модули чисел;
• перед полученным произведением поставить знак «-».
Примеры умножения отрицательных и положительных чисел.
• (- 0,3) • 0,5 = — 1,5
• 1,2 • (- 7) = — 8,4

Правила знаков для умножения
Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.

Минус на минус даёт плюс,
Плюс на минус даёт минус.

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.

При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.
Пример.
(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) =

В примере пять отрицательных множителей. Значит, знак результата будет «минус».
Теперь вычислим произведение модулей, не обращая внимание на знаки.
6 • 3 • 4 • 2 • 12 • 1 = 1728

Конечный результат умножения исходных чисел будет:
(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) = — 1728

Умножение на ноль и единицу
Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.
• 0 • a = 0
• a • 0 = 0
• a • 1 = a
Примеры:
• 0 • (- 3) = 0
• 0,4 • 1 = 0,4
Особую роль при умножении рациональных чисел играет отрицательная единица (- 1).

При умножении на (- 1) число меняется на противоположное.

В буквенном выражении это свойство можно записать:
a • (- 1) = (- 1) • a = — a

При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.

Пример умножения отрицательных и положительных чисел.

Деление отрицательных чисел
Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению.

Если a и b положительные числа, то разделить число a на число b, значит найти такое число с, которое при умножении на b даёт число a.

Данное определение деления действует для любых рациональных чисел, если делители отличны от нуля.

Поэтому, например, разделить число (- 15) на число 5 — значит, найти такое число, которое при умножении на число 5 даёт число (- 15). Таким числом будет (- 3), так как
(- 3) • 5 = — 15

Примеры деления рациональных чисел.
1. 10 : 5 = 2, так как 2 • 5 = 10
2. (- 4) : (- 2) = 2, так как 2 • (- 2) = — 4
3. (- 18) : 3 = — 6, так как (- 6) • 3 = — 18
4. 12 : (- 4) = — 3, так как (- 3) • (- 4) = 12

Из примеров видно, что частное двух чисел с одинаковыми знаками — число положительное (примеры 1, 2), а частное двух чисел с разными знаками — число отрицательное (примеры 3,4).

Правила деления отрицательных чисел
Чтобы найти модуль частного, нужно разделить модуль делимого на модуль делителя.
Итак, чтобы разделить два числа с одинаковыми знаками, надо:
• модуль делимого разделить на модуль делителя;
• перед результатом поставить знак «+».
Примеры деления чисел с одинаковыми знаками:
• (- 9) : (- 3) = + 3
• 6 : 3 = 2

Чтобы разделить два числа с разными знаками, надо:
• модуль делимого разделить на модуль делителя;
• перед результатом поставить знак «-».
Примеры деления чисел с разными знаками:
• (- 5) : 2 = — 2,5
• 28 : (- 2) = — 14
Для определения знака частного можно также пользоваться следующей таблицей.
Правило знаков при делении

При вычислении «длинных» выражений, в которых фигурируют только умножение и деление, пользоваться правилом знаков очень удобно. Например, для вычисления дроби

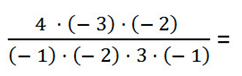
Можно обратить внимание, что в числителе 2 знака «минус», которые при умножении дадут «плюс». Также в знаменателе три знака «минус», которые при умножении дадут «минус». Поэтому в конце результат получится со знаком «минус».

Сокращение дроби (дальнейшие действия с модулями чисел) выполняется также, как и раньше:

Частное от деления нуля на число, отличное от нуля, равно нулю.
0 : a = 0, a ≠ 0
Делить на ноль НЕЛЬЗЯ!

Все известные ранее правила деления на единицу действуют и на множество рациональных чисел.
• а : 1 = a
• а : (- 1) = — a
• а : a = 1
, где а — любое рациональное число.

Зависимости между результатами умножения и деления, известные для положительных чисел, сохраняются и для всех рациональных чисел (кроме числа нуль):
• если a • b = с; a = с : b; b = с : a;
• если a : b = с; a = с • b; b = a : c
Данные зависимости используются для нахождения неизвестного множителя, делимого и делителя (при решении уравнений), а также для проверки результатов умножения и деления.

Пример нахождения неизвестного.
x • (- 5) = 10

Знак «минус» в дробях
Разделим число (- 5) на 6 и число 5 на (- 6).

Напоминаем, что черта в записи обыкновенной дроби — это тот же знак деления, и запишем частное каждого из этих действий в виде отрицательной дроби.

Таким образом знак «минус» в дроби может находиться:
• перед дробью;
• в числителе;
• в знаменателе.

При записи отрицательных дробей знак «минус» можно ставить перед дробью, переносить его из числителя в знаменатель или из знаменателя в числитель.

Это часто используется при выполнении действий с дробями, облегчая вычисления.

Пример. Обратите внимание, что после вынесения знака «минуса» перед скобкой мы из большего модуля вычитаем меньший по правилам сложения чисел с разными знаками.