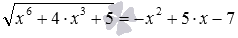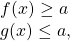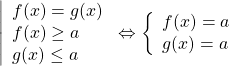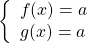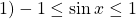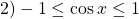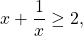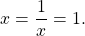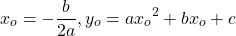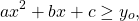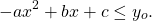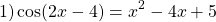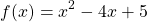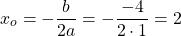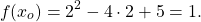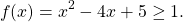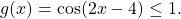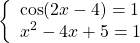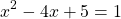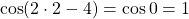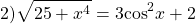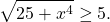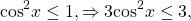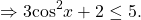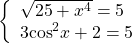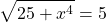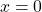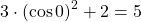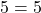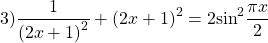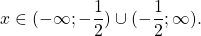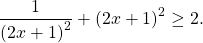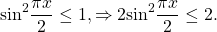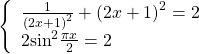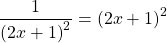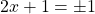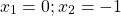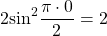Уравнения с корнями метод оценки

Одним из методов решения иррациональных уравнений является метод оценки. В этой статье сначала мы всесторонне разберем, в каких случаях и каким образом иррациональные уравнения решаются методом оценки. А после этого рассмотрим решения большого количества характерных иррациональных уравнений.

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Для решения каких иррациональных уравнений используется метод оценки?

Метод оценки — это одно из направлений функционально-графического метода решения уравнений. А функционально-графический метод обычно используется тогда, когда другие методы не позволяют получить решение. Значит, к методу оценки стоит прибегать лишь тогда, когда нет возможности решить иррациональное уравнение другими более привычными и простыми методами.

Следующим по значимости признаком, склоняющим к использованию метода оценки для решения заданного иррационального уравнения, является очевидная или довольно отчетливо просматривающая возможность получения оценок значений выражений (или оценок значений соответствующих функций), отвечающих частям уравнения.

Дальше нужно смотреть на полученные оценки. Дело в том, что не все оценки позволяют продвинуться в решении заданного уравнения. Подробнее о том, какие оценки позволяют получить решение уравнения, речь пойдет в одном из следующих пунктов.

Итак, к методу оценки для решения иррационального уравнения целесообразно обращаться, если

• не видно более простого метода решения,
• есть возможность оценить значения выражений, отвечающих частям уравнения,
• полученные оценки позволяют продвинуться в решении.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Вспоминаем суть метода

Суть метода оценки состоит в использовании оценок значений частей уравнения для перехода к равносильной системе уравнений или для обоснования отсутствия корней.

Из этого понятно, что решение уравнений методом оценки проводится в два этапа. Первый этап – это оценка значений функции y=f(x) (или соответствующего выражения f(x) , что по сути одно и то же), если решается уравнение f(x)=C , или оценка значений функций y=g(x) и y=h(x) (или соответствующих выражений f(x) и g(x) ), если решается уравнение g(x)=h(x) . Второй этап – это использование полученных оценок для дальнейшего поиска корней уравнения или обоснования их отсутствия.

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Как оцениваются значения выражений?

Этот вопрос детально разобран в отдельной статье Как оценить значения выражения (функции). Здесь мы ограничимся перечислением способов оценки, которые наиболее часто используются при решении методом оценки именно иррациональных уравнений. Вот этот список способов оценки:

• Оценка на основании определения корня с четным показателем. Так как по определению корень с четным показателем есть неотрицательное число, то для любого x из ОДЗ для выражения , где n – натуральное число, p(x) – некоторое выражение, справедливо неравенство , причем тогда и только тогда, когда p(x)=0 .
• Оценка на основании следующего свойства корней: для любых неотрицательных чисел a и b , a ( ≤ , > , ≥ ), выполняется неравенство ( ≤ , > , ≥ ). Если для любого x из ОДЗ для выражения выполняется неравенство p(x) ( ≤ , > , ≥ ), где c – некоторое неотрицательное число, то для любого x из ОДЗ справедливо неравенство ( ≤ , > , ≥ ).
• Оценка на базе того факта, что степень любого числа с четным показателем есть неотрицательное число. Для любого x из ОДЗ для выражения p 2·n (x) справедливо неравенство p 2·n (x)≥0 , причем p 2·n (x)=0 тогда и только тогда, когда p(x)=0 .
• Оценка значений квадратного трехчлена. Для оценки можно использовать ординату вершины параболы, и при отрицательном дискриминанте — ноль.
  • Если a>0 , то a·x 2 +b·x+c≥y₀ , где y₀ – ордината вершины параболы, а если a , то a·x 2 +b·x+c≤y₀ .
  • Если a>0 и дискриминант D , то a·x 2 +b·x+c>0 , а если a и D , то a·x 2 +b·x+c .
• Оценка на базе свойств числовых неравенств.
  • Если на множестве X выполняется условие p(x) ( ≤ , > , ≥ ), где B – некоторое число, то для любого числа C на множестве X будет справедливо неравенство p(x)+C ( ≤ , > , ≥ ). Равенство возможно тогда и только тогда, когда p(x)=B .
  • Если на множестве X выполняется условие p(x) ( ≤ , > , ≥ ), где B – некоторое число, то на множестве X для любого положительного числа C будет справедливо неравенство C·p(x) ( ≤ , > , ≥ ), а для любого отрицательного C – неравенство C·p(x)>C·B ( ≥ , , ≤ ). Равенство возможно тогда и только тогда, когда p(x)=B .
    Следствие. Если на множестве X выполняется условие p(x) ( ≤ , > , ≥ ), где B – некоторое число, то на X справедливо неравенство -p(x)>-B ( ≥ , , ≤ ). Равенство возможно тогда и только тогда, когда p(x)=B .
  • Если на множестве X значения выражения p(x) положительные и выполняется условие p(x) ( ≤ , > , ≥ ), где B – некоторое положительное число, то на X будет справедливо неравенство ( ≥ , , ≤ ).
  • Если на множестве X выполняется условие p₁(x) ( ≤ , > , ≥ ), где B₁, B₂, …, B_n – некоторые числа, то на множестве X справедливо неравенство p₁(x)+p₂(x)+…+p_n(x) ( ≤ , > , ≥ ). Равенство возможно тогда и только тогда, когда одновременно p₁(x)=B₁, p₂(x)=B₂, …, p_n(x)=B_n .
  • Если на множестве X все значения всех выражений p₁(x), p₂(x), …, p_n(x) являются положительными числами и выполняются все условия p₁(x) ( ≤ , > , ≥ ), где B₁, B₂, …, B_n – некоторые положительные числа, то на множестве X справедливо неравенство p₁(x)·p₂(x)·…·p_n(x) ( ≤ , > , ≥ ). Равенство возможно тогда и только тогда, когда одновременно p₁(x)=B₁, p₂(x)=B₂, …, p_n(x)=B_n .
    Следствие. Если на множестве X все значения выражения p(x) есть положительные числа и выполняется условие p(x) ( ≤ , > , ≥ ), где B – некоторое положительное число, то на множестве X справедливо неравенство p n (x) n ( ≤ , > , ≥ ). Равенство возможно тогда и только тогда, когда p(x)=B .
• Оценка через наибольшее и наименьшее значение функции, найденное с использованием производной. Если A — наименьшее значение функции p на множестве X , то на X справедливо неравенство p(x)≥A . Если B — наибольшее значение функции p на множестве X , то на X справедливо неравенство p(x)≤B .

Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Как использовать полученные оценки?

Допустим, с первым этапом мы справились, то есть, оценили значения функций. Возникает логичный вопрос о том, как дальше использовать полученные оценки для решения уравнения. А дальше нужно сослаться на одно из следующих утверждений:

• Уравнение f(x)=C не имеет решений на множестве X в следующих случаях:
  • Если f(x) и A .
  • Если f(x)≤A и A .
  • Если f(x)>B и B>C .
  • Если f(x)≥B и B>C .
  • Если f(x) .
  • Если f(x)>C .
• Уравнение f(x)=C на множестве X равносильно системе уравнений в следующих случаях:
  • Если на множестве X f(x)≤C , причем f(x) представляет собой сумму функций f₁(x), f₂(x), …, f_n(x) таких, что f₁(x)≤C₁, f₂(x)≤C₂, …, f_n(x)≤C_n (при этом C₁+C₂+…+C_n=C ).
  • Если на множестве f(x)≥C , причем f(x) представляет собой сумму функций f₁(x), f₂(x), …, f_n(x) таких, что f₁(x)≥C₁, f₂(x)≥C₂, …, f_n(x)≥C_n (при этом C₁+C₂+…+C_n=C ).
  • Если на множестве X f(x)≤C , причем f(x) представляет собой произведение функций f₁(x), f₂(x), …, f_n(x) таких, что 0≤f₁(x)≤C₁, 0≤f₂(x)≤C₂, …, 0≤f_n(x)≤C_n (при этом C₁·C₂·…·C_n=C ).
  • Если на множестве X f(x)≤C , причем f(x) представляет собой произведение функций f₁(x), f₂(x), …, f_n(x) таких, что f₁(x)≥C₁, f₂(x)≥C₂, …, f_n(x)≥C_n , где числа C₁, C₂, …, C_n — неотрицательные (при этом C₁·C₂·…·C_n=C ).
• Уравнение g(x)=h(x) не имеет решений на множестве X в следующих случаях:
  • Если g(x), h(x)>B и A .
  • Если g(x)≤A , h(x)>B и A .
  • Если g(x), h(x)≥B и A .
  • Если g(x)≤A , h(x)≥B и A .
• Уравнение g(x)=h(x) не имеет решений на множестве X и в следующих случаях:
  • Если g(x) , h(x)>C .
  • Если g(x)≤C , h(x)>C .
  • Если g(x) , h(x)≥C .
• Если на множестве X значения одной из функций g и h не меньше некоторого числа C , а значения другой функции не больше этого числа C , то уравнение g(x)=h(x) равносильно на множестве X системе .

Положения второго блока утверждений следуют из свойств сложения и умножения верных числовых неравенств одного смысла.

Первый блок положений становится понятен, если представить взаимное расположение графика функции f и прямой y=C , а положения остальных блоков – если представить взаимное расположение графиков функций g и h .

Разберем первый блок утверждений. Когда график функции f ниже или не выше прямой y=A , которая в свою очередь ниже прямой y=C , то понятно, что он не пересекается с прямой y=C , из этого вытекает отсутствие корней уравнения f(x)=C . Когда график функции f выше или не ниже прямой y=B , которая в свою очередь выше прямой y=C , то понятно, что он не пересекается с прямой y=C , из этого вытекает отсутствие корней уравнения f(x)=C . Когда график функции f ниже или выше прямой y=С , то понятно, что он не пересекается с этой прямой, из этого также вытекает отсутствие корней уравнения f(x)=C .

Теперь обоснуем третий блок утверждений. Пусть на множестве X значения функции g меньше или не больше числа A , а значения функции h больше или не меньше числа B . Это означает, что все точки графика функции g находятся ниже или не выше прямой y=A , а точки графика функции h – выше или не ниже прямой y=B . Понятно, что на множестве X при A графики функций g и h не будут иметь общих точек, так как график функции g будет расположен ниже графика функции h . А это означает, что уравнение g(x)=h(x) не имеет решений.

Переходим к четвертому блоку утверждений. Здесь в первом случае один график расположен ниже этой прямой, другой – выше этой прямой. Во втором случае один график не выше этой прямой, другой – выше этой прямой. В третьем случае один график ниже этой прямой, другой – не ниже этой прямой. Понятно, что во всех случаях графики не имеют общих точек, значит, уравнение g(x)=h(x) не имеет решений.

В последней ситуации график одной функции не выше прямой y=C , а график другой функции – не ниже этой прямой. При этом понятно, что графики могут иметь общие точки только на этой прямой. Это и объясняет переход от уравнения g(x)=h(x) к системе .

Можно переходить к практике.

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Примеры решения иррациональных уравнений

Рассмотрим решения характерных иррациональных уравнений методом оценки.

Для начала стоит разобраться с вопросом точности оценки значений выражений. Чтобы было понятно, откуда берется такой вопрос, посмотрите на три оценки значений корня : первая , вторая , третья , и скажите, какую предпочесть? Ну, первую отбросим, так как она по большей части надумана, а вот вторая и третья оценки вполне рабочие, и в зависимости от ситуации может быть использована и первая из них, сравнительно грубая, и вторая. Посмотрим на этот вопрос с позиций практики.

Для доказательства того, что уравнение не имеет решений, бывает достаточно грубых оценок. Основное преимущество грубых оценок перед более точными оценками состоит в относительной простоте их получения. Грубые оценки практически очевидны и не требуют дополнительных исследований, так как в их основе лежат хорошо известные факты, такие как: квадратный корень – это неотрицательное число, модуль – это неотрицательное число, квадрат числа – это неотрицательное число, сумма положительных взаимно обратных чисел не меньше двух, значения квадратного трехчлена с отрицательным старшим членом и отрицательным дискриминантом — отрицательные и т.п. Так для решения следующего иррационального уравнения методом оценки достаточно грубой оценки корня с одной стороны и квадратного трехчлена с другой стороны.

Решить иррациональное уравнение

Обычно проще получить грубые оценки значений функций или выражений, чем точные. Но довольно часто грубые оценки не позволяют сделать выводы о корнях решаемых уравнений, в то время как более точные оценки дают такую возможность. Давайте решим типовое иррациональное уравнение.

Решите иррациональное уравнение 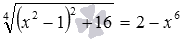методом оценки.

Будем считать, что разобрались, когда применять грубые оценки, а когда более точные. Теперь перейдем к решению методом оценки иррациональных уравнений вида f(x)=C .

Начнем с решения простого, но очень характерного иррационального уравнения: оценка значений его левой части вытекает из оценок составляющих ее корней, и из полученной оценки следует вывод об отсутствии корней уравнения.

Решите уравнение

Интереснее обстоит дело, когда выражение, отвечающее левой части иррационального уравнения f(x)=C , представляет собой сумму или произведение нескольких выражений и его значения оцениваются как f(x)≤C или f(x)≥C . В таких случаях записанные выше утверждения предписывают переходить от исходного иррационального уравнения к равносильной системе уравнений. Приведем решение характерного иррационального уравнения.

Решить иррациональное уравнение методом оценки

Закрепим навыки перехода по методу оценки от иррационального уравнения f(x)=C с суммой или произведением в левой части к равносильной системе уравнений. Для этого решим сравнительно сложное иррациональное уравнение, левая часть которого представляет собой сумму двух иррациональных выражений, одно из которых является произведением двух выражений. Принцип решения тот же: получаем оценку, которая позволяет перейти от исходного уравнения к равносильной системе.

Решите уравнение

Перейдем к иррациональным уравнениям вида g(x)=h(x) .

Предыдущие примеры были довольно простые в плане оценки значений выражений и функций. Пришло время проработать аспект оценки более детально. По понятным причинам упор сделаем на способах оценки, к которым приходится прибегать наиболее часто при решении методом оценки именно иррациональных уравнений. Начнем со способов оценки, не требующих нахождения производной. Так чтобы решить следующее иррациональное уравнение, придется привлечь чуть ли не все известные средства: от свойства степеней с четным показателем и свойства монотонности функции извлечения корня до оценок на базе свойств числовых равенств.

Решить методом оценки иррациональное уравнение

Способы получения оценок, которые мы использовали во всех предыдущих примерах, не закрывают вопрос оценки значений полностью. Другими словами, не всегда с их помощью удается оценить значения функций и выражений. В частности, рассмотренные способы нехороши, когда область допустимых значений переменной x для решаемого иррационального уравнения отлична от множества всех действительных чисел R . В качестве примера приведем оценку корня в двух случаях: когда ОДЗ есть множество R и когда ОДЗ есть отрезок от 3 до 5 . Опираясь на способы оценки, которыми мы пользовались выше, мы можем получить оценку . Для случая, когда ОДЗ есть множество R , эта оценка очень даже хороша. Но для случая, когда ОДЗ есть отрезок [3, 5] , записанная оценка уже оказывается сравнительно грубой, и есть возможность оценить корень более точно, а именно как . Но не только ОДЗ ограничивает возможности получения оценок разобранными выше способами. Часто эти способы не дают возможности оценить значения функции из-за вида оцениваемой функции. Например, способы оценки, о которых мы говорим, позволяют оценить значения корней и , а также их сумму: , , откуда и дальше . Но эти способы оценки уже не позволяют оценить значения разности указанных корней. В подобных ситуациях приходится прибегать к исследованию функции, нахождению ее наибольшего и наименьшего значений, через которые и оценивать значения функции. Иногда удобно комбинировать различные способы получения оценок. Покажем решение характерного иррационального уравнения.

Решите уравнение

Завершая разговор о решении иррациональных уравнений функционально-графическим методом и методом оценки в частности, вспомним про одно обещание, данное в статье Решение иррациональных уравнений методом введения новой переменной. Там, мы решили иррациональное уравнение довольно экзотическим способом через введение двух новых переменных, и обещали показать его решение более стандартным методом. Таким методом в данном случае выступает именно метод оценки. Так выполним обещанное.

Решить иррациональное уравнение методом оценки

Мы разобрались, как и когда применяется метод оценки для решения иррациональных уравнений, а также рассмотрели решения характерных примеров. Продолжим изучать методы решения иррациональных уравнений, для чего обратимся к материалу решение иррациональных уравнений через ОДЗ.

Видео:Алгебра 8 класс. Уравнения с корнямиСкачать

Решение уравнений методом оценки

Решение уравнений методом оценки основано на сравнении области значений функций, стоящих в левой и правой части уравнения.

Если в уравнении

то равенство возможно тогда и только тогда, когда и f(x) и g(x) одновременно равны a:

При этом, если максимальное значение функции, стоящей в одной части уравнения, равно минимальному значению функции, стоящему в другой части уравнения, и эти значения достигаются для обеих функций при x=x0, то xo — корень уравнения.

Графически это можно проиллюстрировать так:

Если максимальное значение функции, стоящей в одной части уравнения, равно минимальному значению функции, стоящему в другой части уравнения, но эти значения достигаются при разных x0, то уравнение не имеет корней:

Получив систему уравнений

достаточно решить одно из уравнений (которое проще), а затем проверить, являются ли найденные корни корнями другого уравнения.

Чаще всего при решении уравнений методом оценки правой и левой части используют следующие соображения:

причём равенство достигается при

4) Квадратичная функция в вершине параболы (x0; y0)

при a>0 принимает своё наименьшее значение:

при отрицательном коэффициенте a при x² — наибольшее значение:

где n — натуральное число.

Примеры решения уравнений методом оценки левой и правой части.

— квадратичная функция. График — парабола ветвями вверх. Наименьшее значение принимает в вершине

С другой стороны

Следовательно, исходное уравнение равносильно системе уравнений

Корень второго уравнения:

x=2. Проверяем, является ли 2 корнем первого уравнения:

— верно. Следовательно, x=2 — единственный корень.

Так как x⁴≥0, то 25+ x⁴≥25, а значит,

С другой стороны,

Следовательно, исходное уравнение равносильно системе уравнений

Решаем первое уравнение

Проверяем, является ли x=0 корнем второго уравнения:

— верно. Значит, x=0 — корень данного уравнения.

Так как сумма взаимно-обратных положительных чисел не меньше двух,

Так как сумма положительных взаимно-обратных чисел равна 2, если эти числа равны между собой, то

Проверяем, являются ли эти корни корнями второго уравнения.

Таким образом, исходное уравнение имеет единственный корень x= -1.

Видео:Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Алгебра

План урока:

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Иррациональные уравнения

Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.

Приведем примеры иррациональных ур-ний:

Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести

Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.

Видео:Метод оценки при решении уравненийСкачать

Простейшие иррациональные уравнения

Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:

где а – некоторое число (константа), f(x) – рациональное выражение.

Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:

Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии

n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.

Ответ: корней нет.

Пример. Решите ур-ние

Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:

Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).

Пример. Найдите решение ур-ния

Решение. Возведем обе части в пятую степень:

х 2 – 14х – 32 = 0

Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:

D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324

Итак, нашли два корня: (– 2) и 16.

Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.

Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:

х – 2 = х 2 – 8х + 16

D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9

Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):

при х = 3 х – 4 = 3 – 4 = – 1

при х = 6 6 – 4 = 6 – 4 = 2

Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.

Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:

3х 2 + 6х – 25 = (1 – х) 3

3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3

Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:

Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.

Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:

при х = 2 1 – х = 1 – 2 = – 1

Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Уравнения с двумя квадратными корнями

Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.

Пример. Решите ур-ние

Решение. Перенесем вправо один из корней:

Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:

Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:

Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:

(2х – 4) 2 = 13 – 3х

4х 2 – 16х + 16 = 13 – 3х

4х 2 – 13х + 3 = 0

D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121

Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:

Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3

На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.

Видео:№12 из ЕГЭ 2022 по профильной математике. Метод оценки - ИМБАСкачать

Введение новых переменных

Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние

Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.

Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:

х 1/2 – 10х 1/4 + 9 = 0

Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид

Это квадратное ур-ние. Найдем его корни:

D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64

Получили два значения t. Произведем обратную замену:

х 1/4 = 1 или х 1/4 = 9

Возведем оба ур-ния в четвертую степень:

(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4

х = 1 или х = 6561

Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:

В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.

Пример. Решите ур-ние

х 1/3 + 5х 1/6 – 24 = 0

Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:

Его корни вычислим через дискриминант:

D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121

Далее проводим обратную заменуx 1/6 = t:

х 1/6 = – 8 или х 1/6 = 3

Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Замена иррационального уравнения системой

Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.

Пример. Решите ур-ние

Решение. Заменим первый корень буквой u, а второй – буквой v:

Исходное ур-ние примет вид

Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:

Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:

Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:

(х + 6) + (11 – х) = u 3 + v 2

из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:

17 = u 3 + (5 – u) 2

17 = u 3 + u 2 – 10u + 25

u 3 + u 2 – 10u + 8 = 0

Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа

подставим полученные значения в (4):

x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3

x + 6 = 1 или х + 6 = 8 или х + 6 = – 64

х = – 5 или х = 2 или х = – 70

Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим

Корень подошел. Проверяем следующее число, х = 2:

Корень снова оказался верным. Осталась последняя проверка, для х = – 70:

Итак, все три числа прошли проверку.

Видео:ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА неравенства с корнемСкачать

Уравнения с «вложенными» радикалами

Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:

При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:

Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:

Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:

Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:

Возводим в квадрат и получаем:

х 2 + 40 = (х + 4) 2

х 2 + 40 = х 2 + 8х + 16

И снова нелишней будет проверка полученного корня:

Видео:Быстрый способ решения квадратного уравненияСкачать

Иррациональные неравенства

По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:

Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.

Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида

Может быть справедливым только тогда, когда

То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во

при четном n можно заменить системой нер-в

Пример. При каких значениях x справедливо нер-во

Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:

х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)

Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во

чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.

Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.

Пример. Найдите решение нер-ва

Решение. Всё очень просто – надо всего лишь возвести обе части в куб:

x 2 – 7x– 8 2 – 7x– 8 = 0

D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81

Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:

Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.

Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.

Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид

Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.

Пример. Решите нер-во

Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):

И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:

D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9

Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.

стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:

f(x) > 0 (подкоренное выражение не может быть отрицательным);

g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).

Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.

Пример. Решите нер-во

Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим

х 2 – 10х + 21 > 0(1)

Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:

Во-вторых, выражение 4 – х не может быть отрицательным:

Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):

Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:

Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:

Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:

Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:

Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).

Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3

🌟 Видео

Решение биквадратных уравнений. 8 класс.Скачать

Система иррациональных уравнений #1Скачать

Иррациональные уравнения и их системы. 11 класс.Скачать

Иррациональные неравенства | Математика ЕГЭ | УмскулСкачать

Как решать иррациональные уравнения. Методы решения иррациональных уравнений. (часть 1).Скачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать