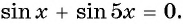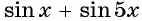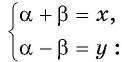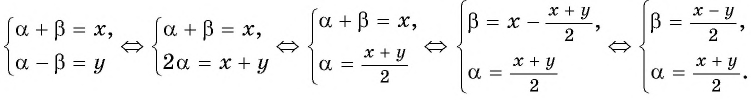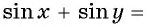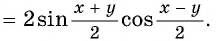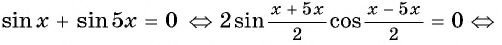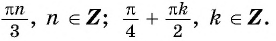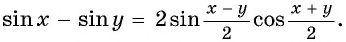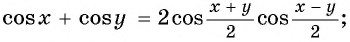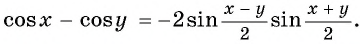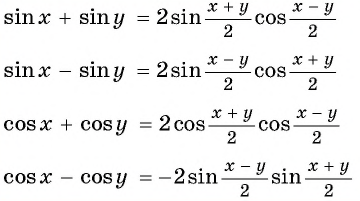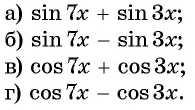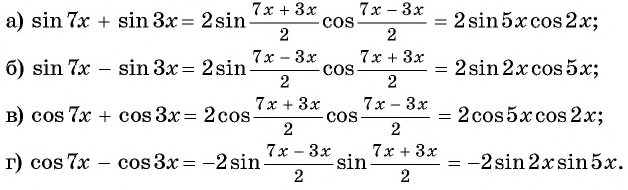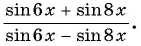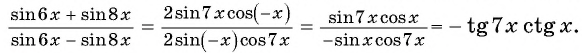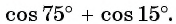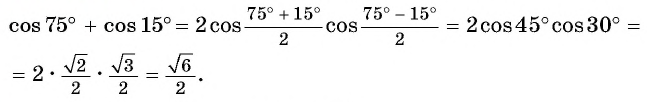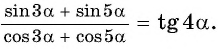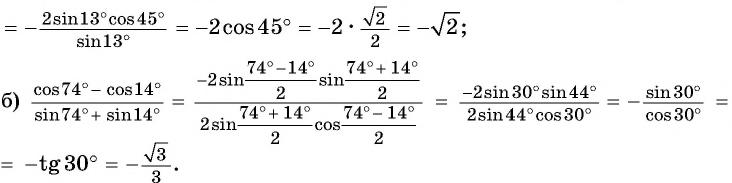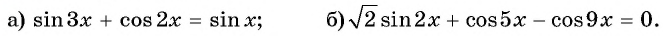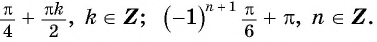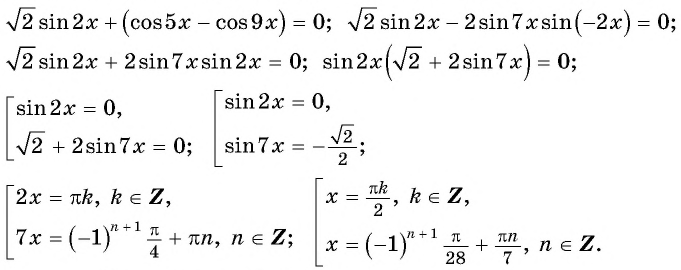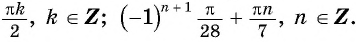п.1. Сумма и разность синусов
Найдем (sinalpha+sinbeta).
Введем новые переменные: (x=frac, y=frac). Тогда (alpha=x+y, beta=x-y). Подставим в сумму и используем формулы синуса суммы и синуса разности (см.§13 данного справочника.
begin sinalpha+sinbeta=sin(x+y)+sin(x-y)=sinx cosy+cosxsiny+\ +sinxcosy-cosxsiny=2sinxcosy=2sinfraccosfrac end
Для вывода формулы разности используем уже найденную формулу суммы и нечетность синуса: begin sinalpha-sinbeta=sinalpha+sin(-beta)=2sinfraccosfrac=\ =2sinfraccosfrac end
п.2. Сумма и разность косинусов
Теперь, используя ту же замену, найдем сумму двух косинусов: begin cosalpha+cosbeta=cos(x+y)+cos(x-y)=cosxcosy-sinxsiny+\ +cosxcosy+sinxsiny=2cosxcosy=2cosfraccosfrac end Для вывода формулы разности используем уже найденную формулу суммы и формулы приведения: begin cosalpha-cosbeta=cosalpha+cos(pi+beta)=2cosfraccosfrac=\ =2cosleft(frac+fracpi2right)cosleft(frac-fracpi2right)=2left(-sinfracright)sinfrac=\ =-2sinfracsinfrac end
Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать
Преобразование сумм тригонометрических функций в произведение (задачи)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На уроке повторяются формулы суммы и разности косинусов и синусов, выводятся формулы суммы и разности тангенсов, решается задача на преобразование в произведение суммы разноименных функций. Также решается несколько примеров на упрощение и решение уравнений.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть уроки
Видео:Формулы преобразования суммы и разности тригонометрических функций в произведение. 9 класс.Скачать
Формулы преобразования суммы и разности синусов (косинусов) в произведение
Формулы синуса суммы и разности двух углов можно использовать для получения новых формул, необходимых для решения уравнений, изучения свойств функций и т. п.
Например, решим уравнение 
Для решения данного уравнения сумму 
Выведем формулу, преобразующую сумму синусов в произведение.
Сложим почленно два равенства:
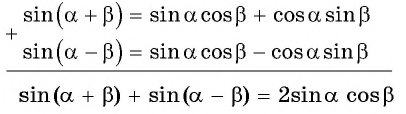
Обозначим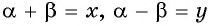 
и решим систему уравнений 
Подставим выражения для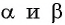 
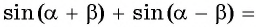
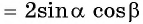
в равенство 
и получим формулу суммы синусов двух углов: 
Вернемся к решению уравнения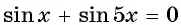 
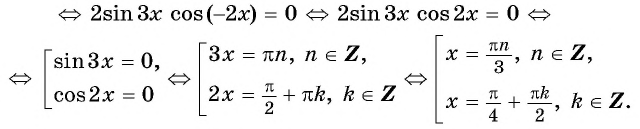
и применим формулу суммы синусов: 
Ответ: 
Вычтя из равенства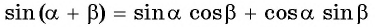 
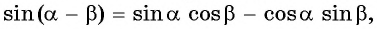
равенство 
можно получить формулу разности синусов двух углов: 
Аналогично, с помощью равенств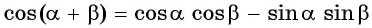 
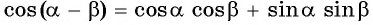
и 
можно получить формулы
- суммы косинусов двух углов:
- разности косинусов двух углов:
Пример:
Представьте в виде произведения:
Решение:
Применим формулы преобразования суммы и разности в произведение и получим:
Пример:
Сократите дробь 
Решение:
Применим формулы суммы и разности синусов двух углов: 
Пример:
Найдите значение выражения 
Решение:
Применим формулу суммы косинусов:
Пример:
Докажите тождество 
Решение:
Воспользуемся формулами суммы синусов и суммы косинусов двух углов:
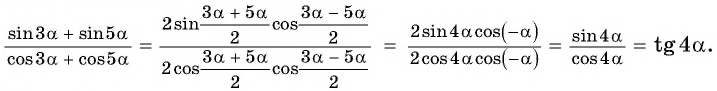
Пример:
Решение:
Пример:
Решение:
а) Запишем уравнение в виде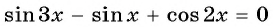 
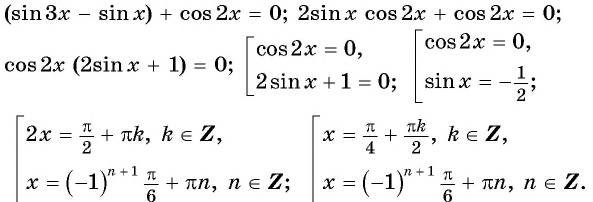
и применим формулу разности синусов:
Ответ: 
б) Воспользуемся формулой разности косинусов и получим:
Ответ: 
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Корень n-й степени из числа и его свойства
- Свойства и график функции y=ⁿ√x (n>1, n∈N)
- Иррациональные уравнения
- Иррациональные неравенства
- Тригонометрические неравенства
- Формулы приведения
- Синус, косинус, тангенс суммы и разности
- Формулы двойного аргумента
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
10 класс, 28 урок, Преобразование суммы тригонометрических функций в произведениеСкачать
§148 Преобразование суммы тригонометрических функций и произведениеСкачать
Формулы преобразования суммы и разности тригонометрических функций в произведение. Практ.ч. 9 класс.Скачать
Формулы преобразования суммы и разности тригонометрических функций в произведение. Практ.ч. 9 класс.Скачать
Формулы преобразования произведения тригонометрических функций в сумму. 9 класс.Скачать
Преобразование сумм тригонометрических функций в произведения | Алгебра 10 класс #36 | ИнфоурокСкачать
Преобразование произведений тригонометрических функций в суммы | Алгебра 10 класс #37 | ИнфоурокСкачать
Решение уравнений с помощью преобразования суммы тригонометрических функций в произведение. Урок #43Скачать
Преобразование суммы тригонометрических функций в произведениеСкачать
Как запомнить формулы преобразования суммы и разности тригонометрических функций в произведениеСкачать
Формулы преобразования суммы и разности тригонометрических функций в произведение. Практ.ч. 9 класс.Скачать
Алгебра 10 класс : Решение примеров на преобразование сумм тригонометрических функций в произведенияСкачать
10 класс - Алгебра - Преобразование сумм тригонометрических функций в произведенияСкачать
Преобразование суммы тригонометрических функций в произведение. От суммы к произведениюСкачать
Алгебра 10 класс: Преобразование сумм тригонометрических функций в произведенийСкачать
9 задание ЕГЭ. Преобразование сумм тригонометрических функций в произведенияСкачать
Преобразование сумм тригонометрическихфункций в произведение.Скачать
Преобразование произведения тригонометрических функций в сумму. От произведения к суммеСкачать
