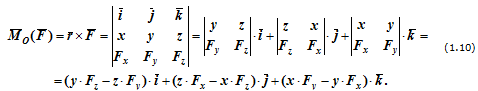Момент силы относительно оси – это характеристика вращательного действия силы на тело, закрепленное на оси, т.е. алгебраический момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью (рисунок 2).
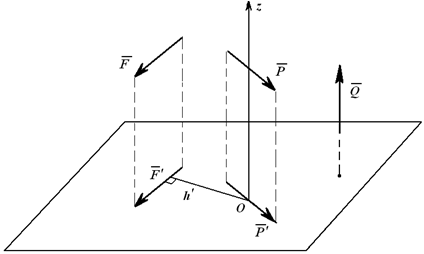
Момент силы относительно, например, оси Oz (рисунок 1), равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси ( F’) относительно точки пересечения оси с плоскостью, т.е.
Момент силы относительно оси – скалярная величина.
Моменты силы относительно координатных осей можно получить, расписав векторное произведение
Величины, стоящие в скобках, представляют собой моменты силы F относительно соответствующих осей.
Наш короткий видеоурок про момент силы с примерами:
- Правило знаков
- Свойства момента силы относительно оси
- Техническая механика
- Пространственная система сил
- Пространственная система сходящихся сил
- Разложение силы по трем осям координат
- Аналитический способ определения равнодействующей пространственной системы сходящихся сил
- Аналитические условия равновесия пространственной системы сходящихся сил
- Момент силы относительно оси
- Аналитические условия равновесия пространственной системы произвольно расположенных сил
- Теорема о моменте равнодействующей относительно оси (теорема Вариньона)
- Лекция по технической иеханике на тему «Пространственная система сил»
- Охрана труда
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 💡 Видео
Видео:Момент силы относительно точки и осиСкачать
Правило знаков
Момент считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки:
где FП – вектор проекции силы F на плоскость П, перпендикулярную к оси Oz, точка O – точка пересечения оси Oz с плоскостью П, h — плечо силы.
Это значит, что момент считается положительным, если мы смотрим навстречу оси и видим проекцию силы, стремящуюся повернуть плоскость чертежа в направлении против хода часовой стрелки.
Момент силы относительно оси равен нулю, если линия действия силы пересекает ось, т.е. h=0 (например Mz(P)), или сила параллельна оси, т.е. ее проекция на плоскость равна нулю, например, Mz(Q).
Видео:§2 4 Аналитические выражения моментов силы относительно осей координатСкачать
Свойства момента силы относительно оси
Момент силы относительно оси обладает следующими свойствами:
- момент равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси;
- момент равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.
Другими словами, момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Урок 80 (осн). Момент силы. Правило моментовСкачать
Техническая механика
Видео:§2 4 Аналитические выражения моментов силы относительно осей координатСкачать
Пространственная система сил
Пространственная система сходящихся сил
Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил .
Пространственная система сил называется сходящейся , если линии действия всех сил системы пересекаются в одной точке.
Теорема: пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Пусть дана пространственная система n сходящихся сил (F1, F2, F3. Fn) . На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма последовательно сложим все силы и получим их равнодействующую:
Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей пространственной системы сходящихся сил неприемлемы, а применяется только аналитический способ (метод проекций) .
Проекция силы на ось в пространстве находится по проецирующим перпендикулярам, и может быть определена при помощи тригонометрических функций. При определении проекций сил пространственной системы потребуется система координат с осями X , Y , Z , поскольку силы системы не располагаются в одной плоскости.
Правило знаков для проекций будет таким же, как и для плоской системы сил – совпадающие по направлению с координатной осью силы считаются положительными, в противном случае – отрицательными. Если вектор силы параллелен какой-либо оси координат, то он проецируется на эту ось в натуральную величину, если же вектор перпендикулярен оси, его проекция на эту ось будет равна нулю.
Разложение силы по трем осям координат
Пусть дана сила F (см. рисунок 1) .
Возьмем систему координат так, чтобы начало координат совпадало с началом вектора силы F (т. е. с точкой приложения силы). Из конца этого вектора опустим перпендикуляр на плоскость xy и разложим силу F на составляющие Fxy и Fz , а составляющую Fxy – на составляющие Fx и Fy . Тогда:
Достроим полученное изображение до параллелепипеда, у которого составляющие Fx , Fy и Fz являются ребрами, а сила F – диагональю.
Из изложенного можно сделать вывод: равнодействующая трех взаимно-перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах .
Из рисунка видно, что в случаях разложения силы F по трем взаимно-перпендикулярным направлениям x , y , z составляющие Fx , Fy и Fz равны по модулю проекциям силы F на эти оси.
Зная проекции силы на три взаимно-перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:
модуль силы: F = √(Fx 2 + Fy 2 + Fz 2 ) (здесь и далее √ — знак корня) ;
направляющие косинусы: cos(F,x) = Fx/F; cos(F,y) = Fy/F; cos(F,z) = Fz/F .
Аналитический способ определения равнодействующей пространственной системы сходящихся сил
Рассмотренный выше способ разложения силы F на три составляющие по направлению координатных осей x , y , z можно применить для каждой из сходящихся сил пространственной системы. Тогда вместо данной системы n сходящихся сил мы получим эквивалентную ей систему 3n сил, из которых n сил действуют по оси x , n сил – по оси y , и n сил – по оси z .
Равнодействующая проекций сил системы на ось x равна их геометрической сумме, то же самое можно сказать и о равнодействующих проекций сил на оси y и z .
Таким образом, систему 3n сил можно заменить эквивалентной ей системой трех сил, каждая из которых представляет собой равнодействующую проекций сил данной системы на ту или иную ось координат.
Проекции силы на три взаимно-перпендикулярные оси и составляющие силы, направленные по этим осям, равны по модулю, следовательно, проекции равнодействующей равны:
Очевидно, что равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах, и по известным проекциям равнодействующей можно определить модуль и направление самой равнодействующей.
Аналитические условия равновесия пространственной системы сходящихся сил
Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система сил находится в равновесии, т. е. эквивалентна нулю, то можно сделать вывод, что равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей тоже равны нулю, причем эти проекции равны сумме проекций составляющих.
Отсюда вытекают условия равновесия пространственной системы сходящихся сил:
ΣX = 0; ΣY = 0; ΣZ = 0 .
Эти условия формируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую их трех координатных осей равнялась нулю.
Момент силы относительно оси
Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (см. рисунок 2) . Червяк передает червячному колесу силу F , не лежащую в плоскости, перпендикулярной оси.
Разложим силу F на три взаимно-перпендикулярные составляющие F1 , F2 и F3 .
Составляющую F1 назовем окружной силой , составляющую F2 – осевой силой , а составляющую F3 – радиальной силой .
Из рисунка видно, что составляющая F1 вызывает вращательное действие, которое измеряется произведением силы F1 на радиус колеса r ; составляющая F2 стремится сдвинуть червячное колесо вдоль оси, а составляющая F3 стремится изогнуть ось колеса.
Очевидно, что вращающее действие сил F2 и F3 относительно оси колеса равно нулю.
Таким образом, если нужно найти момент силы относительно оси, то следует принимать в расчет только составляющую F1 , лежащую в плоскости, перпендикулярной оси, и не пересекающую ось (иначе ее момент будет равен нулю).
Ранее было отмечено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением.
Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Это определение поясняет рисунок 3 .
Момент силы относительно оси условимся записывать следующим образом:
Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, если же сила стремится вызвать вращение по часовой стрелке, ее момент считаем отрицательным.
Момент силы относительно оси не меняется при перемещении силы вдоль оси ее действия.
Момент силы будет равен нулю в двух случаях (не считая случаев, когда сила равна нулю или направлена вдоль оси):
- если вектор силы параллелен оси, так как при этом проекция силы на плоскость, перпендикулярную оси, равна нулю (см. рисунок 3, сила FZ) ;
- если линия действия силы пересекает ось, так как при этом плечо равно нулю (сила F3 на рисунке 2) .
Аналитические условия равновесия пространственной системы произвольно расположенных сил
Пространственная система сил, в которой линии действия составляющих сил расположены произвольно, т. е. линии их действия могут не пересекаться и находиться в разных плоскостях, называется произвольно расположенной системой сил.
Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю.
Строгое обоснование приведенного выше условия равновесия пространственной системы произвольно расположенных сил требует знания некоторых вопросов, не предусмотренных программами учреждений среднего профессионального образования, поэтому условие равновесия такой системы здесь приводится без доказательства.
Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:
- ΣX = 0; ΣMx(Fi) = 0;
- ΣY = 0; ΣMy(Fi) = 0;
- ΣZ = 0; ΣMz(Fi) = 0.
Свободное тело в пространстве имеет шесть степеней свободы, а именно: возможность перемещаться в направлениях трех взаимно-перпендикулярных осей координат и возможность вращаться вокруг этих осей. Таким образом, шести степеням свободы тела в пространстве соответствуют шесть условий равновесия.
Если система сил, приложенных к свободному телу, удовлетворяет всем шести условиям равновесия, то возможность трех перемещений и трех вращений тела под действием сил системы исключена, поэтому тело будет находится в равновесии.
Очевидно, что все выведенные ранее условия равновесия для различных систем сил являются частными случаями условия равновесия пространственной системы произвольно расположенных сил.
Так как условия равновесия пространственной системы сил справедливы для любых прямоугольных осей координат, то при решении данной задачи систему координат можно изменять, т. е. часть уравнений равновесия составить для одних осей координат, а часть – для измененных. В некоторых случаях этот прием упрощает решение задач.
Теорема о моменте равнодействующей относительно оси
(теорема Вариньона)
Теорема: момент равнодействующей относительно оси равен алгебраической сумме моментов, составляющих сил относительно этой же оси .
Пусть даны пространственная система n произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы сил FΣ (см. рисунок 4) :
Приложим к телу другую систему сил, равнодействующая которой F’Σ по модулю равна FΣ и направлена по той же линии действия, но в противоположную сторону, т. е. является уравновешивающей данной системы сил.
Тогда можно записать:
Так как обе записанные выше системы сил эквивалентны нулю, т. е. уравновешены, то к ним можно применить любое условие равновесия, например
Запишем это условие для обеих систем:
Так как правые части этих равенств равны, то будут равны и левые :
Сократив общее слагаемое Mx(F’Σ) , получим:
Видео:Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1Скачать
Лекция по технической иеханике на тему «Пространственная система сил»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Тема: Пространственная система сил
Знать момент силы относительно оси, свойства момента, аналитический способ определения равнодействующей, условия равновесия пространственной системы сил.
Уметь выполнять разложение силы на три взаимно перпендикулярные оси, определять момент силы относительно оси.
Пространственная система сил — система сил, линии действия которых не лежат в одной плоскости.
Момент силы относительно оси
Момент силы относительно оси равен моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью (рис. 1.5.1а).
а — расстояние от оси до проекции F ;
пр F — проекция силы на плоскость, перпендикулярную оси ОО.
Момент считаем положительным, если сила разворачивает тело по часовой стрелке. Смотреть со стороны положительного направления оси.
Если линия действия силы пересекает ось или линия действия силы параллельна оси, моменты силы относительно этой оси равны нулю (рис. 1.5.1б).
Силы и ось лежат в одной плоскости, они не смогут повернуть гело вокруг этой оси.
Пространственная сходящаяся система сил
Вектор в пространстве
В пространстве вектор силы проецируется на три взаимно перпендикулярные оси координат. Проекции вектора образуют ребра тор силы совпадает с диагональю (рис.1.5.2).
Модуль вектора может быть получен из зависимости 
Пространственная сходящаяся система сил
Пространственная сходящаяся система сил — система сил, не лежащих в одной плоскости, линии действия которых пересекаются в одной точке.
Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник (рис.1.5.3), = F 1 + F 2 + F 3 +…+ F n
Доказано, что равнодействующая системы сходящихся сил приложена в точке пересечения линий действия сил системы.
Модуль равнодействующей пространственной системы сходя- 1 Чихся сил можно определить аналитически, использовав метод проекций.
Совмещаем начало координат с точкой пересечения линий действия сил системы. Проецируем все силы на оси координат и суммируем соответствующие проекции (рис.1.5.4). Получим проекции равнодействующей на оси координат:
Рисунок 1.5.3 Рисунок 1.5.4
Модуль равнодействующей системы сходящихся сил определим
по формуле
Направление вектора равнодействующей определяется углами
Произвольная пространственная система сил
Приведение произвольной пространственной системы сил к центру О
Дана пространственная система сил (рис. 1.5.5а). Приведем ее к центру О.
Силы необходимо параллельно перемещать, при этом образуется система пар сил. Момент каждой из этих пар равен произведению модуля силы на расстояние до центра приведения.
В центре приведения возникает пучок сил, который может быть заменен суммарной силой (главный вектор) F гл (рис. 1.5.5б).
Моменты пар сил можно сложить, получив суммарный момент системы М гл (главный момент).
Таким образом, произвольная пространственная система сил приводится к главному вектору и главному моменту.
Главный вектор принято раскладывать на три составляющие, направленные вдоль осей координат (рис. 1.5.5в).
Обычно суммарный момент раскладывают на составляющие: три момента относительно осей координат.
Абсолютное значение главного вектора (рис. 1.5.5б) равно
Абсолютное значение главного момента определяется по формуле
Уравнения равновесия пространственной системы сил
При равновесии F гл = 0; М гл = 0. Получаем шесть уравнений равновесия:
Шесть уравнений равновесия пространственной системы сил соответствуют шести независимым возможным перемещениям тела в пространстве: трем перемещениям вдоль координатных осей и трем вращениям вокруг этих осей.
Примеры решения задач
Пример 1. На тело в форме куба с ребром а = 10 см действуют три силы
(рис.1.5.6). Определить моменты сил относительно осей координат, совпадающих с ребрами куба.
Момент силы относительно оси О x : 
Момент силы относительно оси О y :
Момент силы относительно оси О z
Пример 2. На горизонтальном валу закреплены два колеса, r 1 = 0,4м; r 2 = 0,8м. Остальные размеры — на рис. 1.5.7. К колесу 1 приложена сила F 1 , к колесу 2 — силы F 2 = 12 кН, F 3 = 4кН.
Определить силу F 1 и реакции в шарнирах А и В в состоянии равновесия.
Напомним: 
1. При равновесии выполняются шесть уравнений равновесия.
Уравнения моментов следует составлять относительно опор А и В.
Моменты этих сил относительно соответствующих осей равны нулю.
3. Расчет следует завершить Рисунок 1.5.7
проверкой, использовав дополнительные уравнения равновесия.
1. Определяем силу F 1 , составив уравнение моментов сил относительно оси О z :
2. Определяем реакции в опоре А. На опоре действуют две составляющие реакции (У А ;Х А ).
Составляем уравнение моментов сил относительно оси Ох’ (в
опоре В). ч
Поворот вокруг оси Ох’ не происходит:
Знак «минус» означает, что реакция направлена в противоположную сторону.
Поворот вокруг оси Оу’ не происходит, составляем уравнение моментов сил относительно оси Оу’ (в опоре В):
3. Определяем реакции в опоре В. На опоре действуют две составляющие реакции (ХВ , Y в). Составляем уравнение моментов сил относительно оси Ох (опора А):
Составляем уравнение моментов относительно оси Оу (опора А):
4. Проверка. Используем уравнения проекций
Расчет выполнен верно.
Контрольные вопросы и задания
1. Запишите формулы для расчета главного вектора пространственной системы сходящихся сил.
2. Запишите формулу для расчета главного вектора пространственной системы произвольно расположенных сил.
3. Запишите формулу для расчета главного момента пространственной системы сил.
4. Запишите систему уравнений равновесия пространственной системы сил.
5. Какое из уравнений равновесия нужно использовать для определения реакции стержня R 1г (рис. 1.5.8)?
6. Определите главный момент системы сил (рис. 1.5.9). Точка приведения — начало координат. Координатные оси совпадают с ребрами куба, ребро куба равно 20 см; F 1 = 20 кН; F 2 =30 кН.
Рисунок 1.5.9 Рисунок 1.5.10
7. Определите реакцию Х B (рис. 1.5.10). Вертикальная ось со шкивом нагружена двумя горизонтальными силами. Силы F 1 и F 2 параллельны оси Ох. АО = 0,3 м; ОБ = 0,5 м; F 1 = 2 кН; F 2 = 3,5 кН.
Рекомендация. Составить уравнение моментов относительно оси Оу’ в точке А.
Курс повышения квалификации
Охрана труда
- Сейчас обучается 106 человек из 42 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 228 человек из 54 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 354 человека из 63 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 568 939 материалов в базе
Другие материалы
- 15.03.2018
- 190
- 0
- 15.03.2018
- 6818
- 36
- 15.03.2018
- 528
- 1
- 15.03.2018
- 286
- 0
- 15.03.2018
- 458
- 3
- 15.03.2018
- 259
- 1
- 15.03.2018
- 24720
- 100
- 15.03.2018
- 691
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 15.03.2018 5923
- DOCX 550.4 кбайт
- 78 скачиваний
- Рейтинг: 1 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Маркелова Лидия Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 134084
- Всего материалов: 47
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:§ 2.4. Аналитические выражения моментов силыСкачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
В Забайкалье в 2022 году обеспечат интернетом 83 школы
Время чтения: 1 минута
В Воронеже продлили удаленное обучение для учеников 5-11-х классов
Время чтения: 1 минута
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
Рособрнадзор не планирует переносить досрочный период ЕГЭ
Время чтения: 0 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
💡 Видео
4.2 Проекция силы на ось координатСкачать
§ 2.2. Момент силы относительно осиСкачать
Момент силы относительно точкиСкачать
Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать
Момент силыСкачать
Момент силы относительно осиСкачать
Момент силыСкачать
Момент импульса. 10 класс.Скачать
Урок 109. Момент импульса. Закон сохранения момента импульсаСкачать
Урок 76. Задачи на правило моментовСкачать
момент силы относительно осиСкачать
Урок 94. Вычисление моментов инерции телСкачать
Консультация к устному экзамену. Механика. Часть 4: "Вращение твердых тел"Скачать
