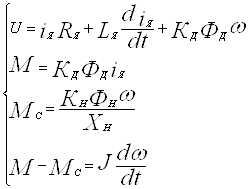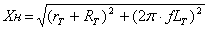Дата добавления: 2015-06-12 ; просмотров: 10005 ; Нарушение авторских прав
Математическое описание ДПТ НВ и его Simulink-модель
Двигатель постоянного тока независимого возбуждения (рис. 4.7), описывается следующей системой дифференциальных и алгебраических уравнений в абсолютных единицах:
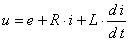 , , | (1) |
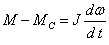 , , | (2) |
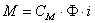 , , | (3) |
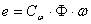 , , | (4) |
u — напряжение на якорной обмотке двигателя,
e — электродвижущая сила (ЭДС) якоря,
Ф — поток, создаваемый обмоткой возбуждения,
M — электромагнитный момент двигателя,
MС — момент сопротивления движению,
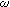
R — активное сопротивление якорной цепи,
L — индуктивность якорной цепи,
J — суммарный момент инерции якоря и нагрузки,
С 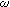
СМ — коэффициент связи между током якоря и электромагнитным моментом.
С точки зрения будущей модели, входными воздействиями являются напряжения якоря u и момент сопротивления движению MС , выходными переменными — электромагнитный момент двигателя M и скорость вращения вала двигателя 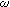
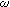
Для создания модели, так же как и в случае насыщающегося реактора, сначала необходимо получить передаточные функции, применив к дифференциальным уравнениям, преобразование Лапласа. Дифференциальное уравнение (1) даст ПФ, связывающую ток якоря и падение напряжения на якоре:
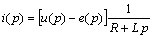 . . | (5) |
Уравнение (2) дает передаточную функцию, связывающую динамический момент и скорость вращения вала двигателя:
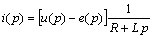 . . | (6) |
Уравнения (3) и (4) остаются без изменений.
В итоге, используя уравнения (3)-(6) не трудно составить Simulink-модель двигателя. Схема модели, а также графики электромагнитного момента и скорости при прямом пуске двигателя показаны на рис. 4.8. В примере приняты следующие значения параметров двигателя (в единицах Си): L=0.001, R=0.1, J=10, Cm=10, Cw=10, U=220, Fi=1. Наброс нагрузки производится в момент времени 0.2с, величина момента нагрузки равна 2500Нм.
Скачать пример (Dpt_Simulink_1.zip)
SPS модель двигателя на базе источника тока
Для создания SPS модели двигателя на базе управляемого источника тока также можно воспользоваться общей схемой, приведенной на рис. 4.1. Выход датчика напряжения должен быть подключен к первому входу сумматора, а на управляющий вход источника тока должен быть подан сигнал пропорциональный току якоря двигателя (выходной сигнал блока Transfer Fcn на рис. 4.8). Схема блока SPS-модели двигателя, полная схема модели, а также графики тока якоря и скорости вращения вала показаны на рис. 4.9.
При работе с моделью двигателя следует иметь в виду, что она не является электротехнической в чистом виде, поскольку выходные сигналы электромагнитного момента и скорости являются обычными однонаправленными безразмерными сигналами Simulink. Графики переменных, представленные на рис. 4.9 полностью повторяют соответствующие графики обычной Simulink модели двигателя, показанные на рис. 4.8.
Скачать пример (Dpt_Powersys_1.zip)
SPS модель двигателя на базе источника напряжения
Модель двигателя постоянного тока можно создать также и на базе управляемого источника напряжения и датчика тока. Поскольку на схеме замещения цепи якоря двигателя (рис. 4.7) присутствуют индуктивность и резистор, то эти элементы можно исключить из Simulink-модели, исключив соответственно и уравнение (1), а также передаточную функцию (5). Сами резистор и индуктивность можно добавить к модели с помощью стандартного блока Series RLC Branch. В результате будет получена комбинированная модель двигателя (рис. 4.10). На рис. 4.10 показана и полная схема модели с подключенным источником питания двигателя (DC Voltage Source). Источник питания подключен через ключ Ideal Switch, который замыкается через небольшой промежуток времени с начала расчета. Наличие такого ключа обусловлено особенностями расчета начальных условий в моделях SimPowerSystem, а именно начальные условия для элемента Series RLC Branch (ток в элементе) задаются как для установившегося режима. Наличие же первоначально разомкнутого ключа обеспечивает нулевые (точнее близкие к нулевым) начальные условия.
Графики переменных двигателя на рис. 4.10 не приведены, поскольку они полностью совпадают с представленными на рис. 4.8 и 4.9.
Скачать пример (Dpt_Powersys_2.zip)
Таким образом, используя изложенную выше методику, пользователь может создавать модели электротехнических устройств различной степени сложности.
5. Библиотека Simulink-прототипов электротехнических блоков.
Электротехнические блоки представленные в библиотеке SimPowerSystem как правило недоступны для просмотра и редактирования их содержимого. Однако, иногда, пользователю необходимо познакомиться с устройством модели хотя бы для того, чтобы лучше разобраться как она работает. Часто пользователя не полностью устраивает библиотечный блок, и он хотел бы внести незначительные изменения для наилучшего решения своей задачи. Весьма полезно также познакомиться с устройством основных блоков для того, чтобы научиться делать их самому. Для реализации перечисленных выше задач в SPS имеется отдельная библиотека Simulink-моделей электротехнических блоков (Simulink-прототипов). Пользователь может открыть библиотеку из основного окна MATLAB, набрав в командной строке powerlib_models. Библиотека прототипов (рис. 5.1) содержит 4 раздела:
· Continuous — непрерывные модели,
· Discrete — дискретные модели,
· Switch Current Source — модели ключей,
· Phasors — модели устройств для расчета установившегося режима.
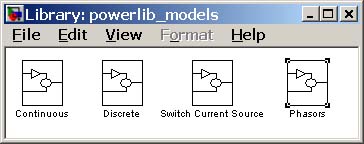
Рис. 5.1
Отличие моделей в этой библиотеке заключается в том, что это обычные Simulink-модели, имеющие однонаправленные входные и выходные порты и соединяющиеся однонаправленными линиями связи, в то время как SPS модели имеют фактически двунаправленные порты и должны соединяться двунаправленными линиями связи. Для создания полноценной SPS на основе прототипа модели разработчику необходимо дополнить прототип источником тока и датчиком напряжения как изложено в главе посвященной пользовательским моделям. Для этого каждый Simulink-прототип имеет вход v, на который нужно подать сигнал пропорциональный напряжению и выход i, подключаемый к источнику тока.
Библиотека Continuous (рис. 5.1) содержит два типа блоков:
· модели электрических машин, насыщающегося трансформатора, грозозащитного разрядника и линии электропередачи с распределенными параметрами,
· блоки логики переключения полупроводниковых устройств с естественной коммутацией (Breaker, Diode, Thyristor и Universal Bridge).
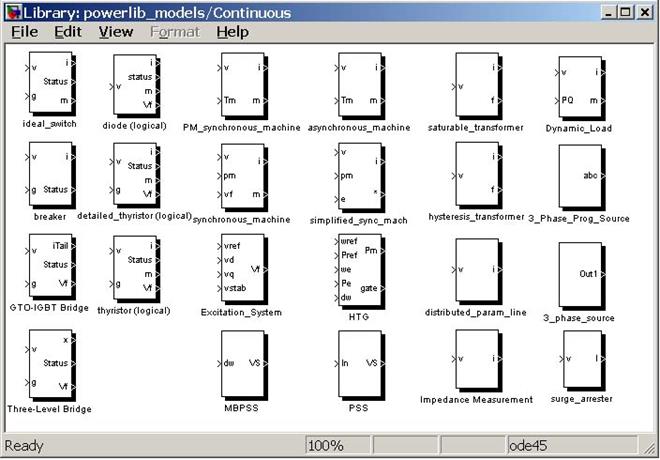
Рис. 5.2
Дискретная библиотека содержит дискретные варианты блоков библиотеки Continuous.
Библиотека Phasors (рис. 5.3) включает модели электрических машин, ключей и линии электропередачи, предназначенные для расчета установившегося режима.
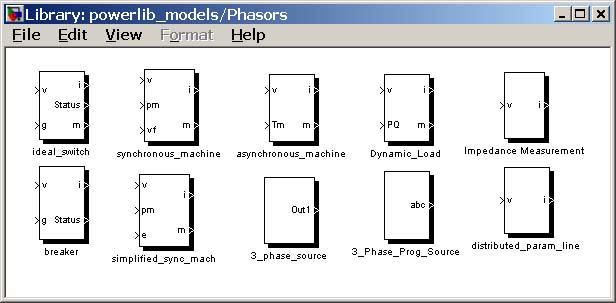
Рис. 5.3
Библиотека Switch Current Source (рис. 5.4) включает модели диода и тиристора, для которых индуктивность во включенном состоянии Lon > 0, а также полностью управляемых полупроводниковых приборов (GTO тиристоров, IGBT и MOSFET транзисторов).
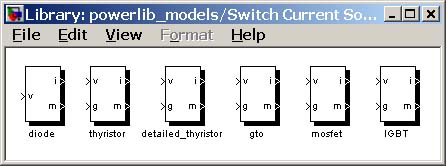
Рис. 5.4
При создании моделей на базе прототипов с использованием источников тока, следует иметь в виду, что такие модели нельзя включать последовательно с индуктивностью. Для устранения этого ограничения следует шунтировать либо индуктивность, либо саму модель резистором с достаточно большим сопротивлением.
6. Основные команды Matlab для управления SPS-моделью.
При разработке графического интерфейса пользователя, создании S-функций и т.п. задач требующих управления конфигурацией, параметрами и работой Simulink и SimPowerSystem моделей допускается использовать специальные команды (функции) языка MATLAB. Для работы с SPS-моделью допускается применять те же самые команды, что и для Simulink моделей (add_line, add_block, get_param, set_param и т.д.). При этом следует иметь в виду, что некоторые Simulink-команды будут иметь ограничения. Так, например, команда set_param не позволяет изменять параметры SPS-блоков в процессе расчета как для Simulink-блоков.
Для SPS-моделей есть и свои особенные команды. Их всего три:
· powerinit — задание начальных условий SPS-модели,
· circ2ss — нахождение математического описания линейной модели электрической цепи в уравнениях пространства состояний,
· power2sys — анализ SPS-модели.
В большинстве случаев пользователю нет необходимости принудительно вызывать эти функции, поскольку они вызываются SimPowerSystem автоматически при начале расчета либо из графической среды пользователя Powergui.
| powerinit | Инициализация SPS-модели |
Задание начальных условий.
powerinit(system,’look’)
Команда выводит начальные значения переменных модели system.
powerinit(system,’reset’)
Команда устанавливает нулевые начальные значения переменных модели system.
powerinit(system,’steady’)
Команда устанавливает начальные значения переменных модели system таким образом, чтобы расчет начался из точки установившегося режима.
powerinit(system,’set’,p)
Команда устанавливает начальные значения переменных модели system заданные в векторе p. Порядок следования переменных можно определить командой powerinit(system,’look’).
powerinit(system,’setb’,state,value)
Команда устанавливает начальное значение value переменной state модели system.
На рис. 6.1 показана модель последовательного колебательного контура подключенного к источнику постоянного тока. Имя файла модели — sys.mdl.
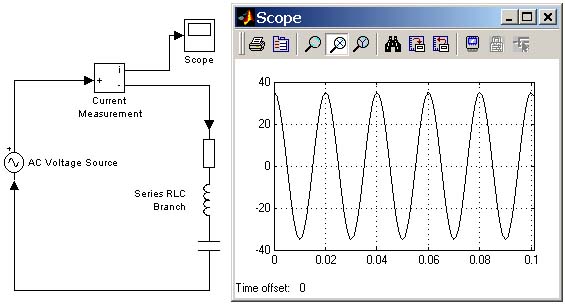
Рис. 6.1
Выполнение команды powerinit(sys,’look’) в окне MATLAB позволяет увидеть начальные значения переменных модели:
Il_Series RLC Branch = 34.8138Uc_Series RLC Branch = -3.8626
На осциллограмме видно, что начальное значение тока контура равно значению найденному с помощью функции powerinit.
Команда powerinit(‘sys’,’setb’,’Il_Series RLC Branch’,-50) задает значение тока в RLC-цепи равное -50А. На рис. 6.2 показана осциллограмма тока для расчета схемы с указанным начальным значением тока.
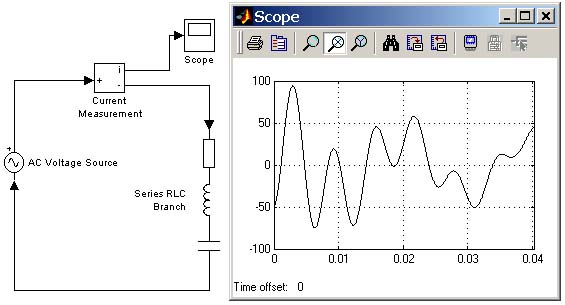
Рис. 6.2
Скачать пример (sys.zip)
| circ2ss | Определение математической модели электрической схемы |
Функция рассчитывает матрицы A, B, C, В уравнений пространства-состояния, описывающих модель:
x = Ax + Buy = Cx + Du
x — вектор состояния,
u — вектор входных воздействий,
y — вектор выходных сигналов,
A, B, C, D — матрицы: системы, входа, выхода и обхода, соответственно.
Функция circ2ss вызывается автоматически функцией power2sys при начале расчета модели. Можно также запускать функцию на выполнение непосредственно из командного окна MATLAB или из m-файла.
Вызов функции должен выполняться минимум для 7 аргументов:
· A, B, C, D — матрицы: системы, входа, выхода и обхода, соответственно.
· states — строковая матрица, содержащая имена переменных состояния. Каждое имя должно находиться в отдельной строке и иметь следующий формат:
· Il_bxx_nzz1_zz2 — ток индуктивности,· Uc_bxx_nzz1_zz2 — напряжение на конденсаторе,
xx — номер ветви,
zz1 — номер первого узла ветви,
zz2 — номер второго узла ветви.
· x0 — вектор начальных значений переменных состояния.
· x0sw — вектор начальных значений токов ключей.
· rlsw — матрица размерностью (nswitch, 2) содержащая значения R(Ом) и L(Гн) ключей, где nswitch — число ключей в схеме.
· u, x, y — матрицы содержащие комплексные значения установившихся величин: u(ninput,nfreq) — входные величины, y(noutput,nfreq) — выходные величины, x(nstates,nfreq) — переменные состояния, где: nfreq — размерность вектора freq, содержащего значения частот источников схемы.
· Asw,Bsw,Csw,Dsw — матрицы уравнений пространства-состояния схемы для закрытых состояний ключей. Каждый закрытый ключ имеющий внутреннюю индуктивность добавляет одну переменную состояния схемы.
· Hlin — трехмерный массив (nfreq, noutput, ninput) комплексных взаимных сопротивлений вход-выход для каждого значения частоты.
· rlc — матрица, задающая топологию схемы.
· switches — матрица ключей, содержащая параметры ключей.
· source — матрица источников, содержащая параметры источников.
· line_dist — матрица линий передачи, содержащая параметры линий передачи.
· yout — строковая матрица, задающая выражения для расчета выходных переменных. Каждое выражение может содержать линейную комбинацию значений переменных состояния и их производных.
· y_type — вектор целых чисел, определяющий вид выходной переменной (0 — напряжение, 1 — ток).
· unit — строковый параметр задающий единицы измерения. Если значения параметра равно ‘OHM’, то значения R, L и С задаются в Ом для базовой частоты, определяемой параметром freq_sys (по умолчанию — 60 Гц). Если значение параметра равно ‘OHU’, то значение R задается в Ом, L — в mГн и С — в мкФ. Функция circ2ss может вызываться также с 12, 13, 14 или 16 аргументами. Подробности о форматах каждого аргумента можно найти в руководстве пользователя для SimPowerSystem.
| power2sys | Определение математической модели электрической схемы, созданной в SimPowerSystem |
Функция рассчитывает матрицы A, B, C, В уравнений пространства-состояния, описывающих модель:
x = Ax + Buy = Cx + Du
x — вектор состояния,
u — вектор входных воздействий,
y — вектор выходных сигналов,
A, B, C, D — матрицы: системы, входа, выхода и обхода, соответственно.
Функция power2sys вызывается автоматически из Simulink при начале расчета модели. Можно также запускать функцию на выполнение непосредственно из командного окна MATLAB или из m-файла.
power2sys(‘sys’,’structure’)
Команда создает структуру для модели sys. Поля структуры имеют тот же смысл, что и данные, возвращаемые функцией circ2ss.
Подробности о способах использования функции power2sys можно найти в руководстве пользователя для SimPowerSystem.
Для модели, показанной на рис. 6.1 вызов функции:
дает следующий результат:
psb = circuit: ‘sys’ states: [2×21 char] inputs: ‘U_AC Voltage Source’ outputs: ‘I_Current Measurement’ A: [2×2 double] B: [2×1 double] C: [1 0] D: 0 x0: [2×1 double] Aswitch: [2×2 double] Bswitch: [2×1 double] Cswitch: [1 0] Dswitch: 0 x0switch: [0x1 double] uss: 100 xss: [2×1 double] yss: 1.2135+34.8138i Hlin: 0.0121+ 0.3481i frequencies: 50 LoadFlow: [] OscillatoryModes: [2×39 char]
Значения полей структуры psb могут быть найдены следующим образом:
>> A=psb.A A = -100 -1000 1000 0 >> B=psb.B B = 1000 0 >> C=psb.C C = 1 0 >> D=psb.C D = 1 0
Остальные поля структуры могут быть найдены аналогично.
Видео:Математическая модель. Видеоурок по алгебре 7 классСкачать

Математическая модель двигателя постоянного тока (ДПТ)
2.1 Математическая модель двигателя постоянного тока (ДПТ)
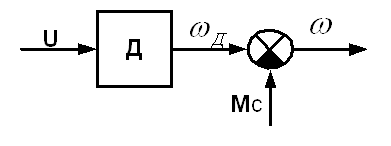
Структурная схема двигателя постоянного тока представлена на рис. 3
Рис. 3 Структурная схема ДПТ
На рис. 3 использованы следующие обозначения:
Мс – момент сопротивления, приложенный к валу двигателя
ωД — скорость вращения вала двигателя
ω – скорость вращения вала с учетом момента сопротивления
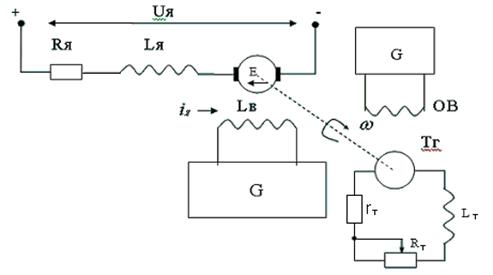
Расчётная схема двигателя постоянного тока независимого возбуждения (ДПТ НВ) представлена на рис. 4.
Рис. 4 Расчётная схема ДПТ
На рис. 4 использованы следующие обозначения:
— Lя – полная индуктивность цепи якоря ДПТ НВ, Гн;
— Rя – полное активное сопротивление цепи якоря, Ом;
— Е – ЭДС вращения якоря, В;
— 
— w – механическая угловая скорость, рад/с;
— Lн – полная индуктивность в цепи якоря тормоза, Гн;
— 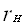
G – источник постоянного напряжения
Kн – коэффициент нагрузки
Фд – магнитный поток
Из литературы известно, что математическая модель ДПТ НВ имеет следующий вид:
где, U – напряжение цепи якоря ДПТ НВ, В;
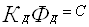
М, Мс – соответственно момент развиваемый двигателем и момент статического сопротивления, развиваемый тормозом на валу двигателя, 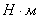
J – момент инерции, 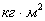
Хн – полное сопротивление цепи нагрузки, Ом.
Подставляя уравнения (2.2) и (2.3) в уравнение (2.4) получаем:
где, 
Продифференцируем данное уравнение и подставим его в уравнение (2.1):

Приведём данное уравнение к стандартному виду
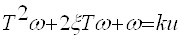

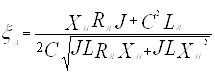
Видео:Алгебра 7 класс. Математический язык. Математическая модельСкачать

Уравнения математической модели дпт нв
Для двигателя постоянного тока (ДПТ) основными уравнениями являются:
— уравнение электрического равновесия 
— уравнение механического равновесия 
— уравнение связи 
Рис.5.1. Структурная схема двигателя постоянного тока
Данным уравнениям соответствует структурная схема рис.5.1.
Если 


Из структурной схемы можно вывести ряд передаточных функций, поскольку есть входные сигналы U, MC, Ф, есть внутренние координаты I, M, есть выходная координата w.
Выведем следующие передаточные функции при Ф = const:





где 


При 

При 
В первом случае полином может быть записан в следующем виде:
Во втором случае имеем комплексные корни:

Характеристический полином получает вид:

где 

На рис. 5.2, 5.3, 5.4 представлены ЛАЧХ для четырех выше выведенных передаточных функций ДПТ при 


Рис.5.2. ЛАЧХ для передаточных функций ДПТ
Рис. 5.3. ЛАЧХ для передаточной функции ДПТ
Рис. 5.4. ЛАЧХ для передаточной функции ДПТ
При комплексных корнях характер ЛАЧХ будет аналогичным, но может появиться небольшой резонансный пик ( 
Цепь намагничивания ДПТ можно представить структурной схемой по рис. 5.5, где

Tвт — постоянная времени вихревых токов в станине и полюсах

Рис.5.5. Структурная схема цепи возбуждения ДПТ.
При регулировании потоком ДПТ существенно нелинейное звено. Во — первых, в структуре рис. 5.1 появляются два блока произведения, во-вторых, надо учитывать нелинейность кривой намагничивания.
Следует отметить, что структурная схема ДПТ при Ф = const рассматривается при постоянстве параметров, т. е. в предположении, что реакция якоря полностью скомпенсирована, активное сопротивление и индуктивность якорной цепи постоянны. Для кривой намагничивания пренебрегаем петлей гистерезиса (при регулировании потоком). Обычно пренебрегаем зависимостью МС от скорости вращения. Однако реально все эти влияния есть и они существенны.
Рассчитаем изменения RЯ при изменении температуры обмотки с 20 °С до 90 °С :
Таким образом, активное сопротивление якорной цепи изменяется на 28 % при переходе от начального включения до рабочей температуры в 90 °С.
Сопротивление 
Сопротивление якорной цепи можно приближенно определить по данным на щитке электрической машины. Полагая, что при работе двигателя в номинальном режиме его постоянные РПОСТ и переменные РПЕР потери равны, получим

ρд = (1 ··· 2) % при Р > 100 кВт;
ρд = (2 ··· 5) % при Р = (100 ··· 5) кВт;
ρд = (5 ··· 10) % при Р = (5 ··· 0,5) кВт;
ρд > 10 % при Р = (0,5 ··· 0,1) кВт.
Экспериментально RЯ находится методом амперметра – вольтметра.
Индуктивность якоря изменяется еще больше, чем сопротивление якорной цепи. Ее рассчитывают

где: n = 0,1 – 0,2 для машин с компенсационной обмоткой (0,25 – для крупных машин); n=0,6 для машин без компенсационной обмотки; рп – число пар полюсов.
Опыты оказывают, что с изменением тока якоря от 0 до пускового индуктивность якоря уменьшается на 30 – 45%.
Экспериментально LЯ определяется по кривой гашения поля [25]. Обмотка якоря подключается к источнику постоянного тока и в некоторый момент замыкается накоротко.
По осцилографируемой кривой IЯ = f(t) (рис. 5.6) можно рассчитать LЯ по уравнению: 
откуда 
Рис. 5.6. Экспериментальное определение ТЯ по кривой гашения поля
Индуктивность обмотки якоря при включенной цепи возбуждения на 15 -20 % меньше, чем при отключенной (сказывается насыщение магнитной цепи). Поэтому опыт желательно проводить при включенной цепи возбуждения.
Определение момента инерции двигателя по геометрическим размерам отдельных вращающихся деталей трудоемок и неточен. Поэтому момент инерции определяется экспериментальным путем по кривой выбега и потерям холостого хода. Двигатель разгоняется до некоторой скорости, а затем отключается от сети, осциллографируется кривая выбега (рис. 5.7.).
Рис. 5.7. Определение момента инерции двигателя по кривой выбега.
Затем определяются потери холостого хода при ряде значений скорости, рассчитывается и строится кривая
Момент инерции определяется следующим образом: 
Значение J определяется для нескольких точек, усредняется, в результате достигается достоверность результатов. Данная методика используется в том числе при определении момента инерции всей системы «двигатель – рабочая машина».
Идентификацию (определение математической модели объекта по экспериментальным данным) удобно производить на ЭВМ, вводя в нее массив точек переходных процессов. В настоящее время в наладочных организациях имеются приборы на основе микроЭВМ, в которые через АЦП данные вводятся автоматически и рассчитываются параметры объекта.
Постоянные времени электромеханической системы могут быть определены методами активной идентификации при подаче на вход воздействия периодического характера. В результате получают ЛАЧХ, по сопрягающим частотам которой определяют постоянные времени.
📽️ Видео
7 класс, 3 урок, Что такое математическая модельСкачать

Моделирование Электротехнических Систем. Прямой пуск ДПТ НВ. Составление схемы в Matlab Simulink.Скачать

Алгебра 7 класс. 7 сентября. Что такое математическая модельСкачать

Тихонов Н. А. - Основы математического моделирования - Типы математических моделей (Лекция 1)Скачать

9 класс, 14 урок, Системы уравнений как математические модели реальных ситуацийСкачать

Математика это не ИсламСкачать

Алгебра 9 класс. Системы уравнений как математические модели реальных ситуацийСкачать

Моделирование Электротехнических Систем. Прямой пуск ДПТ НВ. Решение в MathCad.Скачать

Мат Модель ДПТСкачать

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ//#МАТЕМАТИКА_ПРОСТОСкачать

8 класс, 28 урок, Рациональные уравнения как математические модели реальных ситуацийСкачать

Математическое моделирование - Лекция 1 (09.02.07)Скачать

Информатика. Выпуск 8. Математические модели.Скачать

2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать

Математическое моделированиеСкачать

Математическое моделированиеСкачать

Три этапа математического моделирования.Задача о садовнике. Алгебра 7 классСкачать

Как построить математическую модель оптимизационной задачиСкачать