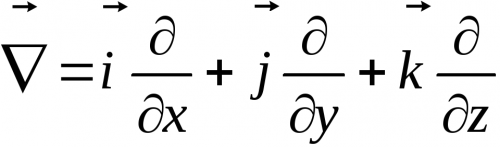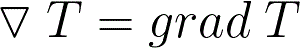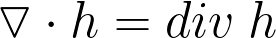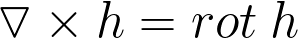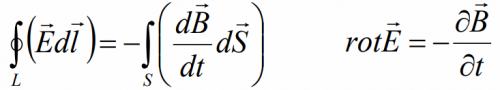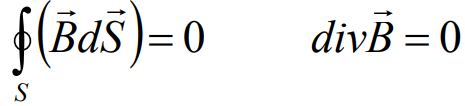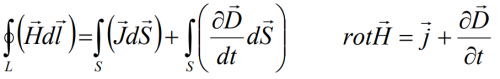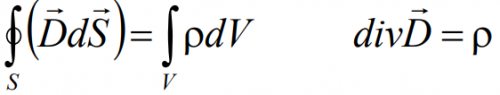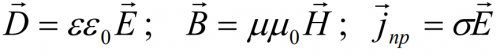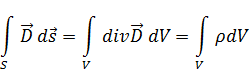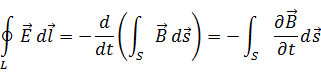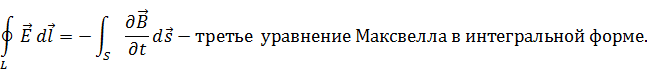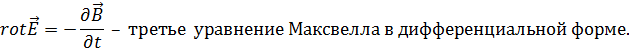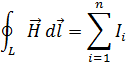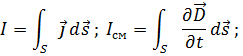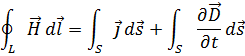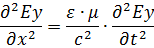Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Уравнения Максвелла

Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.

Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):

1. Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
2. В дальнейшем он вызывает появление магнитного поля.

Видео:ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

Уравнения Максвелла в дифференциальной форме

Уравнение 1: Закон Гаусса или Теорема Гаусса

Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.

Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.

Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.

Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.

Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

Можно создать электрическое поле, изменив магнитное поле.

Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:

1. Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
2. Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
3. Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.

Уравнение 3: Закон Гаусса для магнетизма

Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.

Закон Гаусса для магнетизма утверждает (очень кратко):

1. Магнитных монополей не существует.
2. Расхождение полей B или H всегда равно нулю в любом объёме.
3. На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.

Уравнение 4: Закон Ампера

Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.

Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.

Видео:Уравнения Максвелла и соответствующие уравнения Волновой МоделиСкачать

Уравнения Максвелла в интегральной и дифференциальной форме

Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.

Уравнение 1: Закон Гаусса (Теорема Гаусса)

Это же уравнение в интегральной форме:

Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.

Уравнение 3: Закон Гаусса для магнетизма

И это же уравнение в интегральной форме:

Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.

Уравнение 4: Закон Ампера

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.

Уравнения Максвелла для электромагнитного поля — основные законы электродинамики

Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.

Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.

Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.

Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).

Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.

Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.

В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.

Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.

Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:

где i, j и k – единичные координатные векторы

Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:

Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.

Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.

Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.

Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.

Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.

Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.

Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.

Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.

Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.

Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.

Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.

Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.

Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.

Физический смысл: источником электрического поля является электрический заряд.

Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды:

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Не пропустите обновления, подпишитесь на наши соцсети:

Видео:ЧК_МИФ /ЛИКБЕЗ/ 3_3_5_1 СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА. ПРИМЕРЫ (минимум теории)Скачать

Система уравнений Максвелла для электромагнитного поля.

Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле.

Первое уравнение Максвелла определяет источники электрического поля. Электрические заряды создают вокруг себя электрические поля. Физический смысл этого уравнения состоит в том, что электрическое поле в некоторой области пространства связано с электрическим зарядом внутри этой поверхности.

Исходным для этого уравнения является уравнение Гаусса, которое говорит о том, что поток вектора 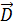через замкнутую поверхность S равен заряду q, заключенному в данной поверхности:

где ρ – объемная плотность заряда.

Для того чтобы получить дифференциальную форму, воспользуемся теоремой Гаусса-Остроградского, которая устанавливает связь между объемным и поверхностным интегралом:

Дивергенция (расходимость) векторного поля – величина мощности источника поля.

Дивергенция является скалярной величиной:

Данное равенство справедливо, если равны подынтегральные функции:

Второе уравнение Максвелла устанавливает для любых магнитных полей отсутствие свободных магнитных зарядов и то, что магнитные силовые линии всегда замкнуты. В интегральном виде этот факт записывается в виде уравнения:

Поток вектора магнитной индукции через замкнутую поверхность равен нулю, поскольку магнитных зарядов одного знака в природе не обнаружено.

Применяя теорему Гаусса – Остроградского:

Третье уравнение Максвелла— это обобщение закона индукции Фарадея для диэлектрической среды в свободном пространстве

где Ф – поток магнитной индукции, пронизывающий проводящий контур и создающий в нем ЭДС.

ЭДС создается не только в проводящем контуре, но и в некотором диэлектрическом контуре в виде электрического тока смещения.

Физический смысл второго уравнения Максвелла состоит в том, что электрическое поле в некоторой области пространства связано с изменением магнитного поля во времени в этой области. Т.е. переменное магнитное поле порождает вихревое электрическое поле.

Воспользуемся уравнением Стокса, которое преобразует контурный интеграл в поверхностный:

Данное равенство справедливо, если равны подынтегральные функции:

Четвертое уравнение Максвелла — это обобщение закона Ампера и Био-Саварра для токов смещения: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему этот контур.

Физический смысл первого уравнения Максвелла состоит в том, что магнитное поле в некоторой области пространства связано не только с токами проводимости, протекающими в этой области, но и с изменением электрического поля во времени в этой области (токами смещения).

Циркуляция вектора по контуру L равна сумме токов проводимости и смещения.

Получим дифференциальную форму уравнения Максвелла. Для этого воспользуемся уравнением Стокса, которое преобразует контурный интеграл в поверхностный:

Данное равенство справедливо, если равны подынтегральные функции:

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

где и – соответственно электрическая и магнитная постоянная,

ε и μ – соответственно диэлектрическая и магнитная проницаемость,

– удельная проводимость вещества.

Уравнение плоской электромагнитной волны (ЭМВ). Поперечный характер ЭМВ. Амплитудные и фазовые соотношения. Скорость распространения электромагнитных волн в средах. Энергия электромагнитной волны. Вектор Пойнтинга.

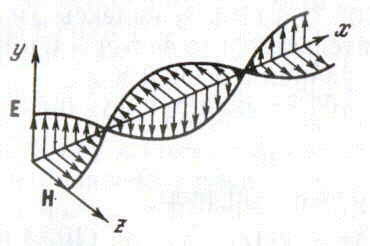
Процесс распространения электромагнитных колебаний в пространстве называется электромагнитной волной. На электромагнитной волне колеблются векторы напряжённости во взаимно перпендикулярных плоскостях в одной фазе – они одновременно обращаются в нуль и одновременно достигают максимальных значений.

Различают плоские, сферические, цилиндрические и другие волны. Простейшими из них являются плоские волны. Плоскойназывается волна, у которой поверхности равных фаз – параллельные плоскости. Если поверхности равных амплитуд совпадают с поверхностями равных фаз, то такая волна называется однородной.

В однородной волне векторы изменяются в пространстве только вдоль одного направления, перпендикулярно фазовому фронту этой волны и совпадающего с направлением ее распространения.

ЭМВ — это поперечные волны, т.е. векторы перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны.

Исследуем плоскую ЭМВ, распространяющуюся в однородной нейтральной 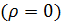непроводящей среде с постоянными проницаемостями .

Тогда уравнения Максвелла принимают вид:

Направим ось x перпендикулярно к волновым поверхностям.

Векторы и их компоненты по осям зависят от одной координаты (х) и от времени (t). Тогда уравнения для имеют вид:

Решения этих уравнений – уравнения электромагнитной волны:

📽️ Видео

Сколько энергии в элементарном заряде. Анализируем первое уравнение МаксвеллаСкачать

О чем говорят уравнения Максвелла? Видео 1/2Скачать

Уравнения Максвелла 2Скачать

Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Теория поля 6. Вторая пара уравнений Максвелла. Законы сохранения ЭМ поля.Скачать

ЧК_МИФ_3_4_4_1_- (L3)___ ТОК СМЕЩЕНИЯ. УРАВНЕНИЯ МАКСВЕЛЛА КАК ФИНАЛ РАЗВИТИЯ КЛАССИЧЕСКОЙ ФИЗИКИСкачать

Чирцов А.С. "Бессильные линии". Уравнения Максвелла. Электромагнитные волны. Оператор. Производная.Скачать

1.1. Решение системы уравнений Максвелла методом интегральных преобразованийСкачать

Уравнения Максвелла 1Скачать

3 14 Уравнения МаксвеллаСкачать

Вывод уравнений МаксвеллаСкачать

Консультация к ГКЭ. Электричество и магнетизм. 1. Уравнения МаксвеллаСкачать

Физические ошибки. Уравнения МаксвеллаСкачать

Уравнения Максвелла 2021Скачать

ЭМ Л28. Телеграфное уравнение. Скорость сигнала. Ток смещения. Уравнения МаксвеллаСкачать

Электромагнитные волны и уравнения Максвелла — Эмиль АхмедовСкачать