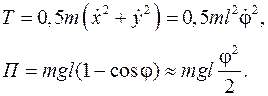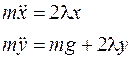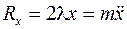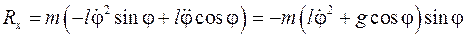- Покажите, что уравнения Ньютона инвариантны относительно преобразований Галилея, а уравнения движения точечной частицы в релятивистской механике ковариантны относительно преобразований Лоренца.
- Приведите вывод законов сохранения энергии, импульса и момента импульса точечной частицы в нерелятивистской и релятивистской механике. Сформулируйте условия, которым должны удовлетворять силы, действующие на частицу.
- Приведите вывод уравнений, определяющих изменение со временем импульса, энергии и момента импульса системы взаимодействующих частиц во внешнем поле при наличии диссипативных сил. Получите уравнение движения тела с переменной массой (уравнение Мещерского).
- Приведите общее решение в квадратурах задачи о движении точечной частицы в центральном поле. Найдите условие замкнутости траектории.
- Найдите общее решение (в квадратурах) задачи двух тел.
- Решение задачи Кеплера методами теории подобия.
- Получите выражение для силы гравитационного взаимодействия частицы с силовым центром, считая известными законы Кеплера.
- Рассмотрите общий случай движения системы отсчета. Найдите уравнения движения материальной точки относительно неинерциальной системы отсчета.
- Упругое рассеяние частиц, поперечные сечения рассеяния.
- Найдите траекторию и угол рассеяния частицы при ее инфинитном движении в поле центральной силы отталкивания с потенциалом U = α/r и силы притяжения с потенциалом U = −α/r.
- Получите формулу для дифференциального эффективного сечения рассеяния жестких сфер.
- Получите формулу Резерфорда для дифференциального сечения рассеяния легких заряженных частиц на первоначально неподвижных тяжелых ядрах.
- Уравнения Лагранжа первого рода. Классификация связей. Реакция связей. Функция Лагранжа.
- Покажите, что функция Лагранжа определена с точностью до полной производной по времени от произвольной скалярной функции координат и времени.
- Считая заданными уравнения голономных идеальных связей, приведите вывод уравнений Лагранжа с реакциями связей 1-го рода. Выведите уравнение изменения полной энергии системы при наличии связей.
- Приведите вывод уравнений Лагранжа для системы N частиц с S степенями свободы из уравнений Даламбера.
- Приведите вывод уравнений Лагранжа из принципа наименьшего действия.
- Ковариантность уравнений Лагранжа относительно точечных преобразований.
- Получить выражение для функции Лагранжа и уравнения движения системы взаимодействующих частиц в неинерциальной системе отсчета.
- Сформулируйте и докажите теорему Нетер и выведите законы сохранения энергии, импульса и момента импульса из требований однородности времени и однородности и изотропности пространства.
- Запишите уравнения Лагранжа в независимых координатах. Циклические координаты.
- Законы сохранения обобщенного импульса и обобщенной энергии.
- Запишите функцию Лагранжа для заряженной массивной частицы в электромагнитном поле.
- Покажите, что общее выражение силы Лоренца вместе с первой парой уравнений Максвелла может быть получено из уравнений Лагранжа для обобщенно-потенциальных сил.
- Установите связь калибровочных преобразований электромагнитного поля с неоднозначностью выбора функции Лагранжа.
- Выведите канонические уравнения Гамильтона из вариационного принципа.
- Приведите определение скобок Пуассона. Докажите теорему Пуассона. Покажите, что множество динамических функций образует алгебру Ли.
- Приведите доказательство теоремы Лиувилля.
- Дайте определение канонических преобразований и приведите производящие функции четырех возможных типов.
- Интегральный инвариант Пуанкаре-Картана. Интегральные инварианты, канонические уравнения и законы сохранения.
- Получить канонические уравнения Гамильтона для системы с S степенями свободы при наличии диссипативных сил, исходя из лагранжевой формы уравнений движения.
- Выведите уравнение Гамильтона-Якоби и докажите теорему Якоби.
- Сформулируйте метод разделения переменных в уравнении Гамильтона-Якоби и его применение для консервативных систем. Продемонстрируйте этот метод на примере.
- Введите переменные «действие-угол» для системы, совершающей условно-периодическое движение. Сформулируйте метод вычисления частот нормальных колебаний системы.
- Адиабатические инварианты. Примеры.
- Приведите доказательство теоремы о вириале для системы частиц с парным потенциалом взаимодействия, зависящим только от расстояний между частицами. Рассмотрите пример кулоновского взаимодействия.
- Исследуйте одномерное движение в консервативном поле. Получите общую формулу для периода нелинейных колебаний. Найдите функцию Лагранжа для одномерного финитного движения частицы во внешнем поле в приближении линейных колебаний и линейное уравнение движения при наличии диссипативной силы, пропорциональной скорости.
- Получите формулы первого приближения методом Крылова-Боголюбова для нелинейных систем с медленно меняющимися параметрами.
- В приближении линейных колебаний найдите общее решение уравнений системы с S степенями свободы при наличии диссипативных сил.
- Вынужденные колебания системы с S степенями свободы под действием периодической внешней силы при наличии диссипативных сил.
- Исследовать общее решение уравнений движения консервативной системы в малой окрестности положения равновесия. Найти условия, при которых система будет оставаться в этой окрестности.
- Написать функцию и уравнения Лагранжа системы с многими степенями свободы в приближении линейных колебаний в нормальных координатах.
- Приведите общее решение задачи о линейных колебаниях линейной симметричной трехатомной молекулы.
- Метод усреднения. Эффективная потенциальная энергия «медленного» одномерного движения системы при наличии высокочастотных возмущений.
Динамика твердого тела
- Уравнения движения твердого тела.
- Приведите формулы преобразований тензора инерции твердого тела при поворотах и параллельных переносах координатных осей. Главные оси инерции. Тензор инерции твердого тела относительно главных осей инерции.
- Исследуйте движение тяжелого симметричного волчка с одной неподвижной точкой.
- Функция Лагранжа твердого тела в случае выбора в качестве обобщенных координат декартовых координат центра масс и углов Эйлера.
- Найти компоненты угловой скорости твердого тела как функции углов Эйлера и их производных по времени.
- Вывод уравнений Эйлера движения твердого тела с одной неподвижной точкой. Частота прецессии свободного симметричного твердого тела.
Механика сплошных сред
- Свойства тензора деформаций сплошной среды.
- Получите полную систему динамических уравнений сплошной среды.
- Получите интеграл Бернулли для стационарного движения идеальной жидкости.
- Выведите уравнение баланса энергии для жидкости.
- Выведите уравнение Навье-Стокса.
- Идеальная жидкость. Условия применимости приближения идеальной жидкости. Уравнение Эйлера.
- Интеграл Коши-Лагранжа для движения идеальной жидкости.
- Несжимаемая жидкость. Уравнения движения несжимаемой жидкости
В каждый экзаменационный билет включены два вопроса и задача по курсу.
Видео:Функция Лагранжа. Уравнения Лагранжа. Интегралы движения.Скачать

Лекция 10. Уравнения Лагранжа 1-го рода
Применяются при решении специальных задач. Прежде всего, их можно применить для определения реакций идеальных связей при движении системы. Достоинством уравнений Лагранжа 2-го рода является отсутствие в них реакций идеальных связей, что существенно облегчает задачу динамики и, вообще, делает ее разрешимой. Найти реакции идеальных связей в этом случае можно способом, основанным на применении принципа освобождаемости от связей. Сначала решается задача по определению законов изменения обобщенных координат, в которой реакции идеальных связей не учитываются. Затем механическая система разнимается по связям, реакции которых необходимо найти. Составляются уравнения Лагранжа 2-го рода для полученных в результате разъема связей частей системы. Туда подставляется найденное ранее решение и таким образом находится значение реакций связей.
Получим уравнения Лагранжа 1-го рода.
Имеем МС с l идеальными связями, уравнения которых
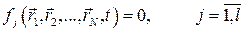
Отсюда, в соответствии с тем, что при варьировании время не меняется, а операция варьирования совпадает с операцией дифференцирования, получим
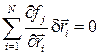
Умножим (10.2) на λj и сложим, получим
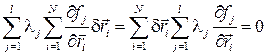
В то же время по свойству идеальности связей
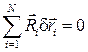
где 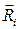
Вычтем из уравнения (10.3) уравнение (10.4), получим
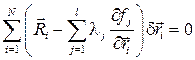
Среди 3N вариаций 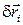
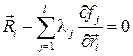
Откуда, находятся все силы реакций идеальных связей
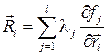
Запишем теперь уравнения движения всех точек системы, исходя из ІІ закона Ньютона
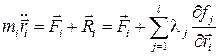
Это и есть уравнения Лагранжа I рода.
В этих 3N уравнениях 3N+l неизвестных, поэтому к ним следует добавить l уравнений связей (10.1).
Рассмотрим пример малых движений математического маятника (рис. 8.1а).
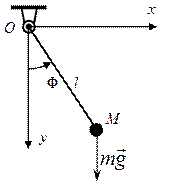 | 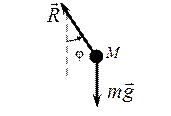 |
Выбрав за обобщенную координату угол поворота оси невесомой нити от вертикали φ, получим
Тогда, согласно уравнениям Лагранжа 2-го рода (5.1), получим
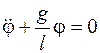

Теперь разрежем нить (освободим точку М от связи) и составим уравнение для точки М, движущейся под действием силы тяжести и силы натяжения нити (рис. 10.1б). Проектируем уравнение движения точки в форме 2-го закона Ньютона на нормаль, получаем
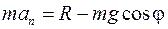
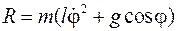
Для одновременного получения закона движения механической системы и действующих в ней реакций связей и служат уравнения Лагранжа 1-го рода.
Составим уравнения движения математического маятника в форме уравнений Лагранжа 1-го рода
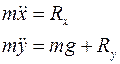
Выразим проекции силы реакции связи через неопределенные множители Лагранжа


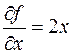
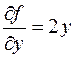
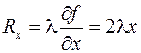

получим уравнения (10.10) в виде
Найдем из первого 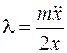

Это уравнение решается заменой
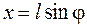
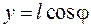
получим уравнение (10.7). Но, одновременно,
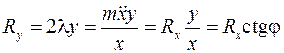
После подстановки в первое уравнение заменяющей формулы (10.12) и уравнения (10.7), окончательно, получим
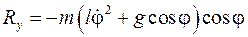
Видео:Теоретическая механика. Лекция №1: Уравнения ЛагранжаСкачать

ИДЕАЛЬНЫЕ СВЯЗИ. УРАВНЕНИЯ ЛАГРАНЖА ПЕРВОГО РОДА. ВАРИАЦИОННЫЙ ПРИНЦИП ДАЛАМБЕРА-ЛАГРАНЖА
Сформулируем принцип освобожлаемости от связей: связи, наложенные на перемещения точек системы, можно отбросить, заменив их воздействие на точки силами (реакциями связей), и рассматривать после этого движение системы как движение системы свободных материальных точек под действием активных сил и реакций связей.
Согласно принципу освобождаемости от связей уравнения движения системы примут вид
Здесь 91 = (R, . R/v). R, — реакция связей, действующая на точку Mh F/— активная сила. К уравнениям (7.1) следует добавить уравнения связей
🎦 Видео
Механическая система со связями. Идеальные связи и уравнения Лагранжа 1-го рода.Скачать

Уравнения Лагранжа второго рода. Задача 1Скачать

Уравнения Лагранжа второго родаСкачать

Несвободное движение точки. Уравнение ЛагранжаСкачать

Форш П. А. - Теоретическая механика - Формализм Лагранжа. Уравнения Лагранжа для материальной точкиСкачать

Халилов В. Р. - Теоретическая механика - Принцип Даламбера. Уравнение ЛагранжаСкачать

№1. Уравнения Лагранжа 2 рода. Задача 1.Скачать

Теормех. 2021-окт-15. Группа РФЗ. Уравнения Лагранжа.Скачать

Уравнение ЛагранжаСкачать

Связи и их реакцииСкачать

Уравнения Лагранжа #1Скачать

Дифференциальное уравнение Лагранжа II рода. Расчет механической системы.Скачать

Халилов В. Р. - Теоретическая механика - Функция и уравнение ЛагранжаСкачать

Связи и реакции связейСкачать

Численное решение системы уравнений Лагранжа I родаСкачать

Вывод уравнения Лагранжа 2-го родаСкачать

Уравнения Лагранжа | Теоретическая механика | Сергей СемендяевСкачать

Халилов В. Р. - Теоретическая механика - Основная задача механики. Виды связейСкачать